文章目录
15.1 聚类概述
“物以类聚人以群分",现实生活中很多事物都存在类似现象,当然这些现象反映在数据上,就需要我们通过一定算法,找出这些类或族。聚类算法就是解决类似问题而提出的。
聚类就是按照某个特定标准(如距离准则)把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同数据尽量分离。
目前,有大量的聚类算法。而对于具体应用,聚类算法的选择取决于数据的类型、聚类的目的。如果聚类分析被用作描述或探查的工具,可以对同样的数据尝试多种算法,以发现数据可能揭示的结果。
主要的聚类算法可以划分为如下几类:划分方法、层次方法、基于密度的方法、基于网格的方法以及基于模型的方法
每一类中都存在着得到广泛应用的算法,例如:划分方法中的k-means聚类算法、层次方法中的层次聚类算法、基于模型方法中的高斯混合聚类算法等。
目前,聚类问题的研究不仅仅局限于上述的硬聚类,即每一个数据只能被归为一类,模糊聚类也是聚类分析中研究较为广泛的一个分支。模糊聚类通过隶 属函数来确定每个数据隶属于各个簇的程度,而不是将一个数据对象硬性地归类到某一簇中。目前已有很多关于模糊聚类的算法被提出,如著名的高斯混合聚类等。
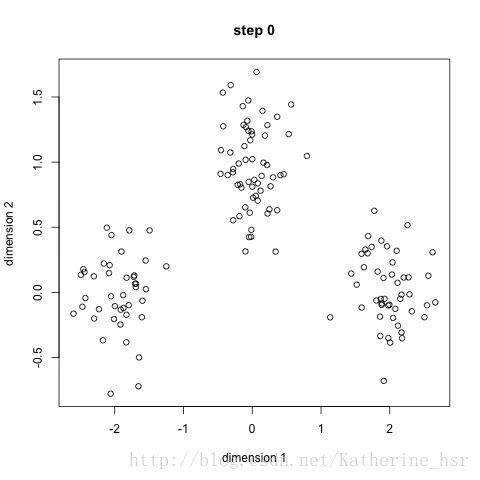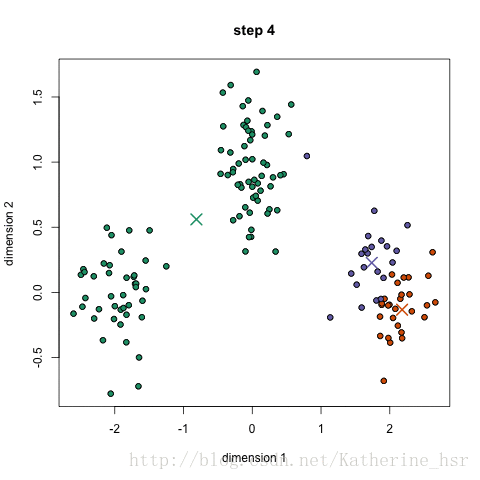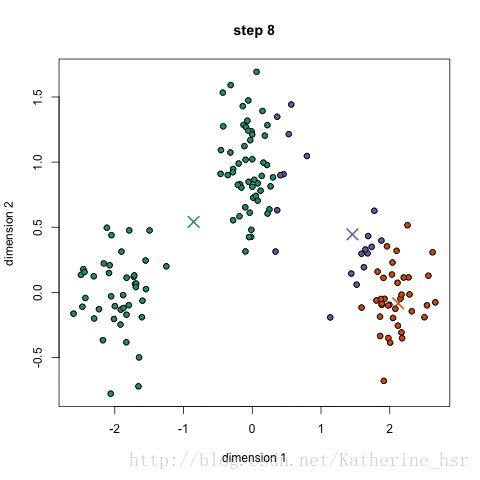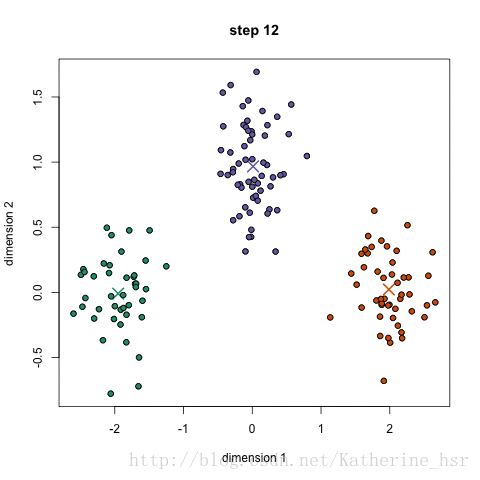
下图演示了K-Means进行聚类的迭代过程:
下图为高斯混合聚类迭代过程:

15.2 k-means模型
算法步骤:
(1)首先我们选择一些类/组,并随机初始化它们各自的中心点。
(2)计算每个数据点到中心点的距离,数据点距离哪个中心点最近就划分到哪一类中。
(3)重新计算每一类中心点作为新的中心点,各中心点求每个类中的平均值。
(4)重复以上步骤,直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点,然后选择运行结果最好的一个。
优点:
计算简便
缺点:
我们必须提前知道数据有多少类/组。
15.3 简单实例
假定我们有如下8个点:
A1(2, 10) A2(2, 5) A3(8, 4) A4(5, 8) A5(7, 5) A6(6, 4) A7(1, 2) A8(4, 9)
现希望分成3个聚类(即k=3)
初始化选择 A1(2, 10), A4(5, 8) ,A7(1, 2)为聚类中心点,假设两点距离定义为ρ(a, b) = |x2 – x1| + |y2 – y1| . (当然也可以定义为其它格式,如欧氏距离)
第一步:选择3个聚类中,分别为A1,A4,A7

这些点的分布图如下:
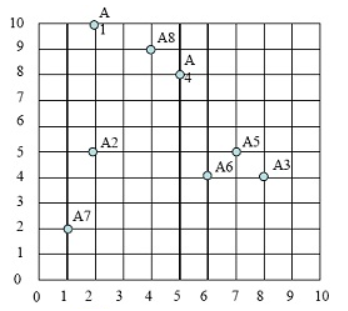
图1
第二步:计算各点到3个类中心的距离,那个点里类中心最近,就把这个样本点
划归到这个类。选定3个类中心(即:A1,A4,A7),如下图:
图2
对A1点,计算其到每个cluster 的距离
A1->class1 = |2-2|+|10-10}=0
A1->class2 = |2-5|+|10-8|=5
A1->class3 = |2-1|+|10-2|=9
因此A1 属于cluster1,如下表:
(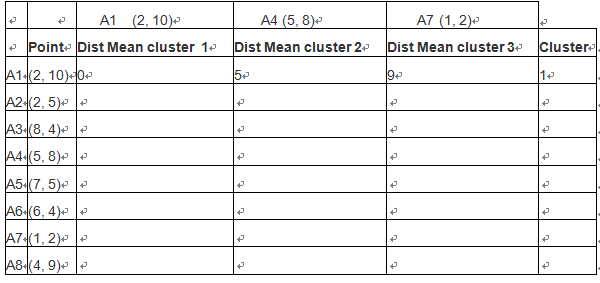
按照类似方法,算出各点到聚类中心的距离,然后按照最近原则,把样本点放在那个族中。如下表:
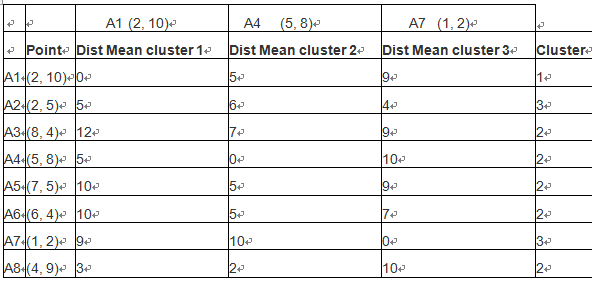
根据距离最短原则,样本点的第一次样本划分,如下图: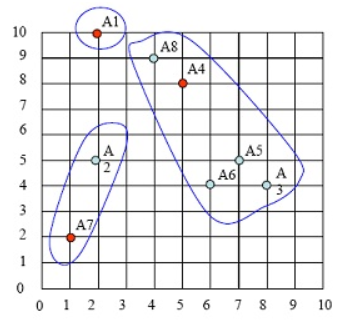
图3
第三步:求出各类中样本点的均值,并以此为类的中心。
cluster1只有1个点,因此A1为中心点
cluster2的中心点为 ( (8+5+7+6+4)/5,(4+8+5+4+9)/5 )=(6,6)。注意:这个点并非样本点。
cluster3的中心点为( (2+1)/2, (5+2)/2 )= (1.5, 3.5),
新族的具体请看下图中x点:
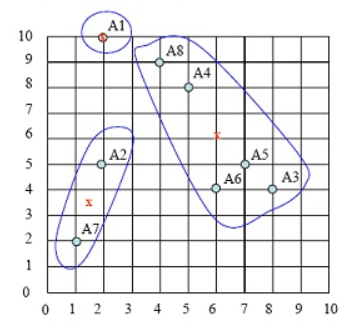
图4
第四步:计算各样本点到各聚类中心的距离,重复以上第二、第三步,把样本划分到新聚类中,如下图: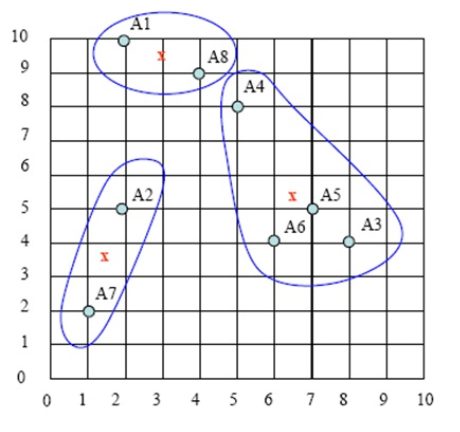
图5
持续迭代,直到前后两次迭代不发生变化为止,如下: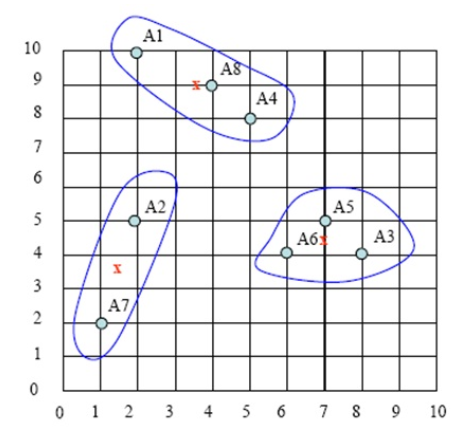
图6
15.4 简单实例用Python实现
(1)生成数据
|
1 2 |
from numpy import * dataSet=array([[2,10],[2,5],[8,4],[5,8],[7,5],[6,4],[1,2],[4,9]]) |
(2)创建距离函数
|
1 2 3 4 5 6 7 8 |
def distabs(vecA, vecB): ''' # 计算两个向量的距离,用的是差的绝对值 :param vecA: :param vecB: :return: 距离 ''' return sum(abs(vecA - vecB)) |
(3)手工选择3个聚类中心
|
1 2 3 4 5 6 7 8 9 10 11 |
def selectCent(dataSet, k): ''' :param dataSet: 输入需聚类的数据集 :param k: 划分的簇数 :return: 返回 k 个簇的初始随机中心数组 ''' centroids = [] for j in [0,3,6]: dataSet[j] centroids.append(dataSet[j]) return array(centroids) |
(4)创聚类函数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
def kMeans(dataSet, k,max_times=6, distMeas=distabs, createCent=selectCent): ''' # K-mean 算法实现 :param dataSet: 需聚类的数据集 :param k: 要划分的簇数 :param max_times:最高迭代次数 :param distMeas: 距离的度量算法,默认方法为 distabs(即差的绝对值距离) :param selectCent: 生成初始的质心 :return: 返回 K 个簇的中心以及划分过后的数据集 ''' m = shape(dataSet)[0] # 创建一个数据划分空间 clusterAssment = mat(zeros((m, 2))) # 获取初始簇中心点 centroids = createCent(dataSet, k) clusterChanged = True while clusterChanged or max_times < 0: max_times -= 1 clusterChanged = False for i in range(m): minDist = inf minIndex = -1 for j in range(k): # 获取每个点到中心 k 的欧几里得距离 distJI = distMeas(centroids[j, :], dataSet[i, :]) # 选择最小距离 if distJI < minDist: minDist = distJI minIndex = j # 判断中心点是否变化 if clusterAssment[i, 0] != minIndex: clusterChanged = True clusterAssment[i, :] = minIndex, minDist ** 2 # 重新计算中心 for cent in range(k): # 获取这个簇中的所有点 ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A == cent)[0]] # 分配质心为平均值 centroids[cent, :] = mean(ptsInClust, axis=0) return centroids, clusterAssment |
(5)运行
|
1 |
kMeans(dataSet,3) |
运行结果
(array([[3, 9],
[7, 4],
[1, 3]]), matrix([[ 0., 4.],
[ 2., 9.],
[ 1., 1.],
[ 0., 9.],
[ 1., 1.],
[ 1., 1.],
[ 2., 1.],
[ 0., 1.]]))
这个运行结果与图6的结果一致。
15.5 简单实例用sklearn实现
(1)导入需要的库或模块
|
1 2 3 4 5 6 7 8 9 10 11 |
%matplotlib inline import numpy as np #科学计算包 import matplotlib.pyplot as plt #python画图包 from matplotlib.font_manager import FontProperties from sklearn.cluster import KMeans #导入K-means算法包 import matplotlib.font_manager as fm ###便于中文显示 #myfont = fm.FontProperties(fname='/home/hadoop/anaconda3/lib/python3.6/site-packages/matplotlib/mpl-data/fonts/ttf/simhei.ttf') myfont = FontProperties(fname=r"c:\windows\fonts\simkai.ttf", size=14) |
(2)创建数据
|
1 2 |
X=np.array([[2,10],[2,5],[8,4],[5.0,8],[7,5],[6,4.0],[1,2],[4,9]]) y=np.array([0,1,1,1,1,2,2,2]) |
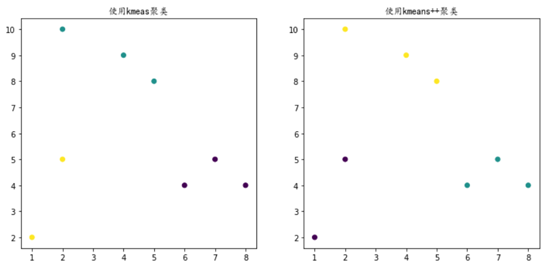
(3)利用kmeans进行聚类,并把结果可视化
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
plt.figure(figsize=(12, 12)) ''''' centers:产生数据的聚类中心点,默认值3 init:采用随机还是k-means++等(可使聚类中心尽可能的远的一种方法) random_state:随机生成器的种子 ''' random_state = 10 # 使用k-means聚类 plt.subplot(221) #在2图里添加子图1 y_pred = KMeans(n_clusters=3, init='random',random_state=random_state).fit_predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.title("使用kmeas聚类",fontproperties=myfont,size=12) #加标题 #使用kmeans++聚类 y_pred = KMeans(n_clusters=3, init='k-means++',random_state=random_state).fit_predict(X) plt.subplot(222)#在2图里添加子图2 plt.scatter(X[:, 0], X[:, 1], c=y_pred) plt.title("使用kmeans++聚类",fontproperties=myfont,size=12) plt.show() |
15.6 简单实例用Tensorflow实现
这里需要用到很多tensorflow函数,大家可参考:
https://www.cnblogs.com/wuzhitj/p/6648563.html
(1)导入需要的库,初始化参数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import tensorflow as tf import numpy as np import time import matplotlib import matplotlib.pyplot as plt from sklearn.datasets.samples_generator import make_blobs #样本数 N=8 #族数 K=3 #最大迭代数 MAX_ITERS = 20 changed = True iters = 0 |
(2)创建数据集,并可视化三个族中心
|
1 2 3 4 5 6 7 |
centers = [(2, 10.0), (5, 8), (1, 2)] data=np.array([[2,10],[2,5],[8,4],[5.0,8],[7,5],[6,4.0],[1,2],[4,9]]) features=np.array([0,1,1,1,1,2,2,2]) fig, ax = plt.subplots() #s-表示标记的大小 ax.scatter(np.asarray(centers).transpose()[0], np.asarray(centers).transpose()[1], marker = 'o', s = 250) plt.show() |
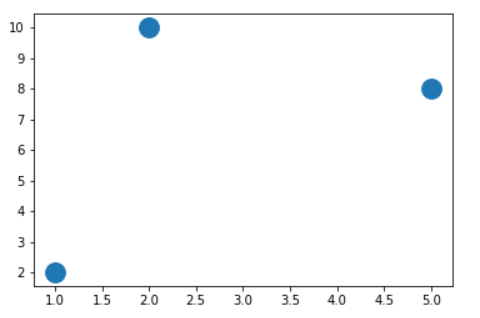
(3)可视化样本
|
1 2 3 4 |
fig, ax = plt.subplots() ax.scatter(np.asarray(centers).transpose()[0], np.asarray(centers).transpose()[1], marker = 'o', s = 250) ax.scatter(data.transpose()[0], data.transpose()[1], marker = 'o', s = 100, c = features, cmap=plt.cm.coolwarm ) plt.show() |
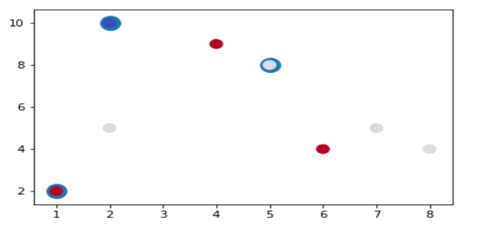
(4)计算各样本的到各族中心距离
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
points=tf.Variable(data) cluster_assignments = tf.Variable(tf.zeros([N], dtype=tf.int64)) centroids = tf.Variable(tf.slice(points.initialized_value(), [0,0], [K,2])) sess = tf.Session() sess.run(tf.global_variables_initializer()) sess.run(centroids) #为计算每点对族中心的距离,使rep_centroids、rep_points都变为NxKx2矩阵 rep_centroids = tf.reshape(tf.tile(centroids, [N, 1]), [N, K, 2]) rep_points = tf.reshape(tf.tile(points, [1, K]), [N, K, 2]) sum_squares = tf.reduce_sum(tf.square(rep_points - rep_centroids),2) #获取最小值的对应索引值 best_centroids = tf.argmin(sum_squares, 1) #判断所有族中心是否不再变化 did_assignments_change = tf.reduce_any(tf.not_equal(best_centroids, cluster_assignments)) |
(5)定义函数,更新各族中心坐标
|
1 2 3 4 5 6 7 8 9 |
#定义函数,更新各族中心坐标 def bucket_mean(data, bucket_ids, num_buckets): total = tf.unsorted_segment_sum(data, bucket_ids, num_buckets) count = tf.unsorted_segment_sum(tf.ones_like(data), bucket_ids, num_buckets) return total / count means = bucket_mean(points, best_centroids, K) #确定执行依赖关系,先执行did_assignments_change,然后执行后续命令 with tf.control_dependencies([did_assignments_change]): do_updates = tf.group(centroids.assign(means),cluster_assignments.assign(best_centroids)) |
(6)可视化迭代过程
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
fig, ax = plt.subplots() colourindexes=[2,1,3] #循环停止条件是族中心不再变化而且循环次数不超过指定值 while changed and iters < MAX_ITERS: fig, ax = plt.subplots() iters += 1 [changed, _] = sess.run([did_assignments_change, do_updates]) [centers, assignments] = sess.run([centroids, cluster_assignments]) ax.scatter(sess.run(points).transpose()[0], sess.run(points).transpose()[1], marker = 'o', s = 200, c = assignments, cmap=plt.cm.coolwarm ) ax.scatter(centers[:,0],centers[:,1], marker = '^', s = 550, c = colourindexes, cmap=plt.cm.plasma) ax.set_title('Iteration ' + str(iters)) plt.savefig("kmeans" + str(iters) +".png") ax.scatter(sess.run(points).transpose()[0], sess.run(points).transpose()[1], marker = 'o', s = 200, c = assignments, cmap=plt.cm.coolwarm ) plt.show() |
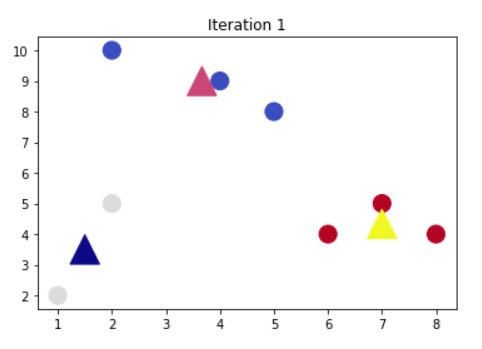
迭代1次就到达最佳结果,看来是要tensorflow效果不错!
15.7 改进
由于 K-means 算法的分类结果会受到初始点的选取而有所区别,因此有提出这种算法的改进: K-means++。其实这个算法也只是对初始点的选择有改进而已,其他步骤都一样。初始质心选取的基本思路就是,初始的聚类中心之间的相互距离要尽可能的远。整个算法的过程如下:
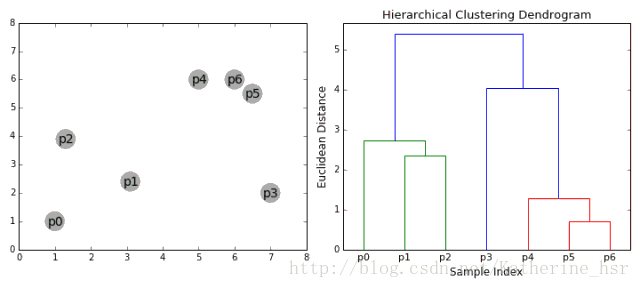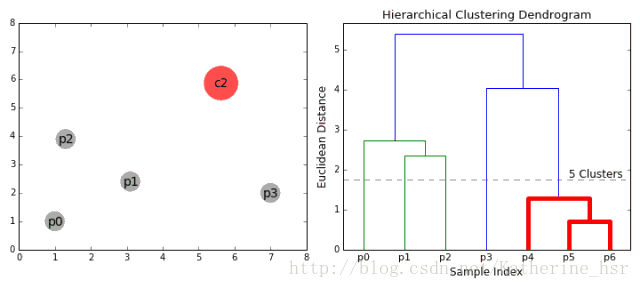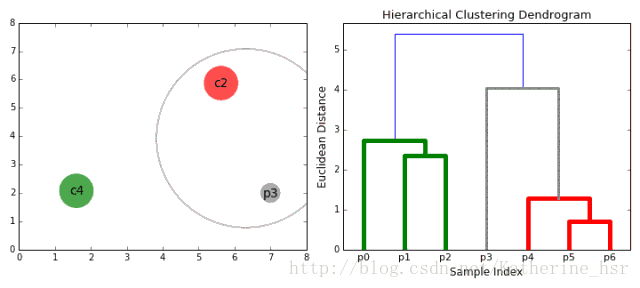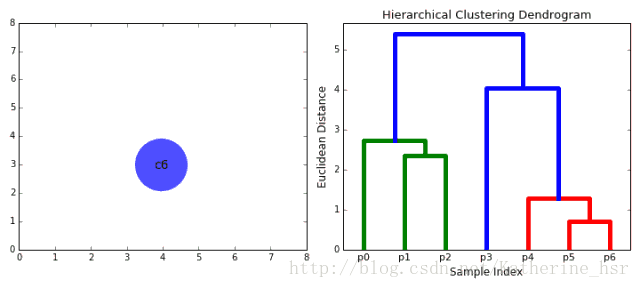
下面结合一个简单的例子说明K-means++是如何选取初始聚类中心的。数据集中共有8个样本,分布以及对应序号如下图所示: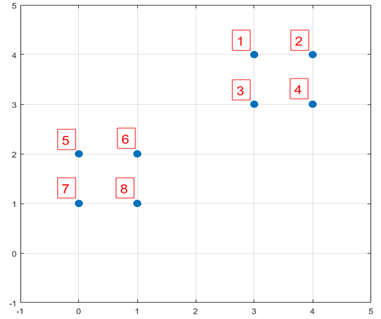
图7
假设经过图7的步骤一后6号点被选择为第一个初始聚类中心,那在进行步骤二时每个样本的D(x)和被选择为第二个聚类中心的概率如下表所示:
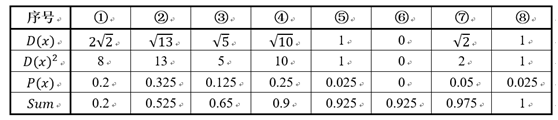
其中的P(x)就是每个样本被选为下一个聚类中心的概率。最后一行的Sum是概率P(x)的累加和,用于轮盘法选择出第二个聚类中心。方法是随机产生出一个0~1之间的随机数,判断它属于哪个区间,那么该区间对应的序号就是被选择出来的第二个聚类中心了。例如1号点的区间为[0,0.2),2号点的区间为[0.2, 0.525)。
从上表可以直观的看到第二个初始聚类中心是1号,2号,3号,4号中的一个的概率为0.9。而这4个点正好是离第一个初始聚类中心6号点较远的四个点。这也验证了K-means的改进思想:即离当前已有聚类中心较远的点有更大的概率被选为下一个聚类中心。可以看到,该例的K值取2是比较合适的。当K值大于2时,每个样本会有多个距离,需要取最小的那个距离作为D(x)。
Pingback引用通告: Python与人工智能 – 飞谷云人工智能