第20章深度学习框架Pytorch快速入门

文章目录

20.1 Pytorch简介
20.2Pytorch安装配置
20.3Pytorch实例
20.3.1利用Numpy实现正向和反向传播（简单实例）
20.3.2利用Numpy实现正向和反向传播（一般情况）
20.3.3Pytorch的Tensor实现正向和反向传播
20.3.4利用Tensor和autograd实现自动反向传播
20.3.5拓展autograd
20.3.6对比TensorFlow
20.3.7高级封装（nn模块）
20.3.8 优化器（optim）
20.3.9 自定义网络层
20.3.10 控制流与参数共享
20.3.11 小试牛刀：用Tensor实现线性回归
20.3.12 小试牛刀：用nn训练CIFAR10

20.1 Pytorch简介

PyTorch 是 Torch 在 Python 上的衍生. 因为 Torch 是一个使用 Lua 语言的神经网络库,由于 PyTorch 采用了动态计算图（dynamic computational graph）结构，PyTorch 有一种独特的神经网络构建方法：使用和重放 tape recorder。而不是大多数开源框架，比如 TensorFlow、Caffe、CNTK、Theano 等采用的静态计算图。使用 PyTorch，通过一种我们称之为「Reverse-mode auto-differentiation（反向模式自动微分）」的技术，你可以零延迟或零成本地任意改变你的网络的行为。
torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运。
torch是一个支持 GPU 的 Tensor 库,如果你使用 numpy，那么你就使用过 Tensor（即 ndarray）。PyTorch 提供了支持 CPU 和 GPU 的 Tensor。
pytorch版本变化

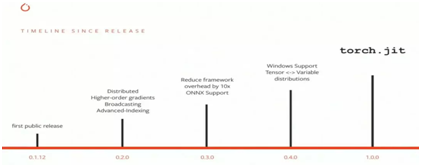
从 2015 年谷歌开源 TensorFlow 开始，深度学习框架之争越来越越激烈，全球多个看重 AI 研究与应用的科技巨头均在加大这方面的投入。从 2017 年年初发布以来，PyTorch 可谓是异军突起，短短时间内取得了一系列成果，成为了其中的明星框架。
PyTorch 1.0 预览版已出，稳定版发布在即，全新的版本融合了 Caffe2 和 ONNX 支持模块化、面向生产的功能，并保留了 PyTorch 现有的灵活、以研究为中心的设计。PyTorch 1.0 从 Caffe2 和 ONNX 移植了模块化和产品导向的功能，并将它们和 PyTorch 已有的灵活、专注研究的设计结合，已提供多种 AI 项目的从研究原型制作到产品部署的快速、无缝路径。利用 PyTorch 1.0，AI 开发者可以通过混合前端快速地实验和优化性能，该前端可以在命令式执行和声明式执行之间无缝地转换。PyTorch 1.0 中的技术已经让很多 Facebook 的产品和服务变得更强大，包括每天执行 60 亿次文本翻译。
pytorch的组成：
PyTorch由4个主要包装组成：
①.torch：类似于Numpy的通用数组库，可以在将张量类型转换为（torch.cuda.TensorFloat）并在GPU上进行计算。
②.torch.autograd：用于构建计算图形并自动获取渐变的包。
③.torch.nn：具有共同层和成本函数的神经网络库。
④.torch.optim：具有通用优化算法（如SGD，Adam等）的优化包。

20.2Pytorch安装配置

本章的环境：python3.6，pytorch0.4.1，windows
windows下安装pytorch0.4.1的方法如下：

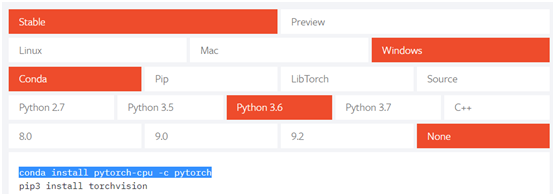
登录pytorch官网（https://pytorch.org/），选择安装配置内容，具体如下：

在命令行输入以下安装命令：

conda install pytorch-cpu -c pytorch

1	conda install pytorch-cpu -c pytorch

验证pytorch安装是否成功及安装版本号：

import torch
print(torch.__version__)

1 2	import torch print(torch.__version__)

运行结果
0.4.1

20.3Pytorch实例

我觉得入门最快、最有效的方法就是实战，通过一些实际案例的学习，收获往往要好于从简单概念入手。本节内容安排大致如下：
先从我们熟知的numpy开始，看如何使用numpy实现正向传播和反向传播开始，接着介绍与pytorch中与Numpy相似的Tensor，如何实现同样功能，然后依次介绍如何使用autograd、nn、optim等等模块实现正向传播和反向传播。最后介绍两个完整实例：一个是回归分析、一个是卷积神经网络。

20.3.1利用Numpy实现正向和反向传播（简单实例）

利用numpy进行正向传播和反向传播，我们先介绍一个简单实例，然后由此推广到一般情况，最后用Pytorch实现自动反向传播。
简单实例主要信息如下：
数据量（N）为1，输入数据维度或节点数（D_in）为2，隐含层节点(H)为2，输出层维度或节点数（D_out）为2，输入到隐含层的权值矩阵为w1,隐含层到输出层的权值矩阵为w2，隐含层的激活函数为Relu(np.maximum(h, 0))，网络结构及矩阵、向量信息如下：
简单示例的神经网络结构图为：

1、正向传播
正向传播示意图（看蓝色细线部分）：

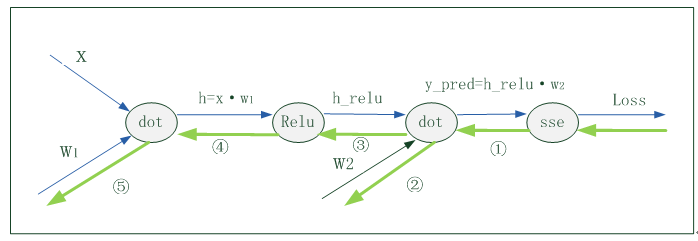
具体实现步骤如下：
（1）导入需要的库或模块
这个简单实例，主要用到numpy及相关运算。

import numpy as np

1	import numpy as np

（2）生成输入数据、权重初始值等

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 1, 2, 2, 2

# 用随机数生成输入数据x及目标数据y
x = np.arange(1,3).reshape(N, D_in)
y = np.arange(1,3).reshape(N, D_out)

# 初始化权重参数
w1 =np.arange(0,0.4,0.1).reshape(D_in, H)
w2 =np.arange(0,0.4,0.1).reshape(H, D_out)

print('x的值:{0},\ny的值:{1},\nw1的初始值:{2},\nw2的初始值:{3}'.format(x,y,w1,w2))

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 1, 2, 2, 2

# 用随机数生成输入数据x及目标数据y

x = np.arange(1,3).reshape(N, D_in)

y = np.arange(1,3).reshape(N, D_out)

# 初始化权重参数

w1 =np.arange(0,0.4,0.1).reshape(D_in, H)

w2 =np.arange(0,0.4,0.1).reshape(H, D_out)

print('x的值:{0},\ny的值:{1},\nw1的初始值:{2},\nw2的初始值:{3}'.format(x,y,w1,w2))

运行结果
x的值:[[1 2]],
y的值:[[1 2]],
w1的初始值:[[0. 0.1]
[0.2 0.3]],
w2的初始值:[[0. 0.1]
[0.2 0.3]]
（3）前向传播并计算预测值

# Forward pass: compute predicted y
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
print('h的值:{0},\nh_relu的值:{1}, \ny_pred的初始值:{2}'.format(h,h_relu,y_pred))

# Forward pass: compute predicted y

h = x.dot(w1)

h_relu = np.maximum(h, 0)

y_pred = h_relu.dot(w2)

print('h的值:{0},\nh_relu的值:{1}, \ny_pred的初始值:{2}'.format(h,h_relu,y_pred))

运行结果
h的值:[[0.4 0.7]],
h_relu的值:[[0.4 0.7]],
y_pred的初始值:[[0.14 0.25]]

其中dot是numpy实现内积运算，该运算规则示意图如下：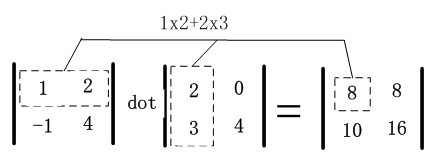

（4）计算损失值

# Compute and print loss
loss = np.square(y_pred - y).sum()
print(loss)

# Compute and print loss

loss = np.square(y_pred - y).sum()

print(loss)

3.8021

2、反向传播
反向传播示意图（看绿色粗线部分）

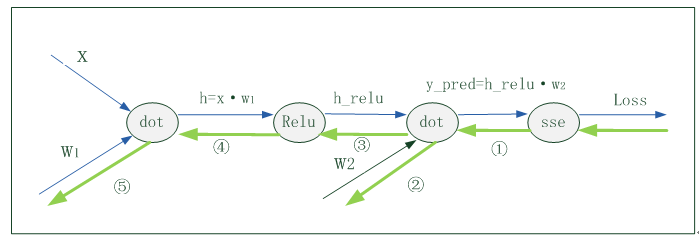
（1）具体求导步骤如下

#基于损失函数，对参数w1，w2进行反向传播。
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()  #深度复制
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
print('对y_pred求导:{0},\n对W2求导:{1}, \n对h_relu求导:
{2}'.format(grad_y_pred,grad_w2,grad_h_relu))
print('h的值:{0},\n对h求导:{1}, \n对w1求导:{2}'.format(grad_h,grad_w2,grad_w1))

#基于损失函数，对参数w1，w2进行反向传播。

grad_y_pred = 2.0 * (y_pred - y)

grad_w2 = h_relu.T.dot(grad_y_pred)

grad_h_relu = grad_y_pred.dot(w2.T)

grad_h = grad_h_relu.copy() #深度复制

grad_h[h < 0] = 0

grad_w1 = x.T.dot(grad_h)

print('对y_pred求导:{0},\n对W2求导:{1}, \n对h_relu求导:

{2}'.format(grad_y_pred,grad_w2,grad_h_relu))

print('h的值:{0},\n对h求导:{1}, \n对w1求导:{2}'.format(grad_h,grad_w2,grad_w1))

运行结果
对y_pred求导:[[-1.72 -3.5 ]],
对W2求导:[[-0.688 -1.4 ]
[-1.204 -2.45 ]],
对h_relu求导:[[-0.35 -1.394]]
h的值:[[-0.35 -1.394]],
对h求导:[[-0.688 -1.4 ]
[-1.204 -2.45 ]],
对w1求导:[[-0.35 -1.394]
[-0.7 -2.788]]
（2）根据梯度更新权重参数

# 根据梯度更新权重参数
learning_rate = 1e-6
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
print('更新w1:{0},\n更新w2:{1}'.format(w1,w2))

# 根据梯度更新权重参数

learning_rate = 1e-6

w1 -= learning_rate * grad_w1

w2 -= learning_rate * grad_w2

print('更新w1:{0},\n更新w2:{1}'.format(w1,w2))

运行结果

更新w1:[[3.50000000e-07 1.00001394e-01]
[2.00000700e-01 3.00002788e-01]],
更新w2:[[6.88000000e-07 1.00001400e-01]
[2.00001204e-01 3.00002450e-01]]
其中涉及对向量或矩阵求导公式推导可参考：
https://blog.csdn.net/DawnRanger/article/details/78600506
至此利用numpy求正向和反向传播就结束了，接下来，我们看一般情况，即包含批量数据、一般维度、对权重进行多次迭代运算。

20.3.2利用Numpy实现正向和反向传播（一般情况）

上节我们用一个简单实例，说明如何利用numpy实现正向和反向传播，有了这个基础之后，我们接下来介绍利用numpy实现一般情况的正向和反向传播，具体代码如下：

# -*- coding: utf-8 -*-
import numpy as np

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y。
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)

# 随机初始化权重参数
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)

learning_rate = 1e-6
for t in range(500):
    # 进行前向传播，计算预测值y_pred
    h = x.dot(w1)
    h_relu = np.maximum(h, 0)
    y_pred = h_relu.dot(w2)

    #计算及打印损失值
    loss = np.square(y_pred - y).sum()
    print(t, loss)

    # 反向传播，基于损失函数计算参数的梯度
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h_relu.T.dot(grad_y_pred)
    grad_h_relu = grad_y_pred.dot(w2.T)
    grad_h = grad_h_relu.copy()
    grad_h[h < 0] = 0
    grad_w1 = x.T.dot(grad_h)

    # 根据梯度更新参数
    w1 -= learning_rate * grad_w1
    w2 -= learning_rate * grad_w2

# -*- coding: utf-8 -*-

import numpy as np

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y。

x = np.random.randn(N, D_in)

y = np.random.randn(N, D_out)

# 随机初始化权重参数

w1 = np.random.randn(D_in, H)

w2 = np.random.randn(H, D_out)

learning_rate = 1e-6

for t in range(500):

# 进行前向传播，计算预测值y_pred

h = x.dot(w1)

h_relu = np.maximum(h, 0)

y_pred = h_relu.dot(w2)

#计算及打印损失值

loss = np.square(y_pred - y).sum()

print(t, loss)

# 反向传播，基于损失函数计算参数的梯度

grad_y_pred = 2.0 * (y_pred - y)

grad_w2 = h_relu.T.dot(grad_y_pred)

grad_h_relu = grad_y_pred.dot(w2.T)

grad_h = grad_h_relu.copy()

grad_h[h < 0] = 0

grad_w1 = x.T.dot(grad_h)

# 根据梯度更新参数

w1 -= learning_rate * grad_w1

w2 -= learning_rate * grad_w2

20.3.3Pytorch的Tensor实现正向和反向传播

Numpy是一个很棒的框架，但它不能利用GPU来加速其数值计算。对于现代深度神经网络，GPU通常提供50倍或更高的加速，所以不幸的是，numpy对于现代深度学习来说还不够。
在这里，我们介绍最基本的PyTorch概念：Tensor。 PyTorch Tensor在概念上与numpy数组相同：Tensor是一个n维数组，PyTorch提供了许多用于在这些Tensors上运算的函数。 Tensors可以跟踪计算图和梯度，也可用作科学计算的通用工具。
与numpy不同，PyTorch Tensors可以利用GPU加速其数值计算。要在GPU上运行PyTorch Tensor，只需将其转换为新的数据类型即可。
在这里，我们使用PyTorch Tensors将双层网络与随机数据相匹配。像上面的numpy示例一样，我们需要手动实现通过网络的正向和反向传播：

# -*- coding: utf-8 -*-

import torch
#定义tensor数据类型
dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)

# 用随机值初始化权重参数
w1 = torch.randn(D_in, H, device=device, dtype=dtype)
w2 = torch.randn(H, D_out, device=device, dtype=dtype)

learning_rate = 1e-6
for t in range(500):
    # 前向传播，计算预测值y_pred
    h = x.mm(w1)
    h_relu = h.clamp(min=0)
    y_pred = h_relu.mm(w2)

    #计算及打印损失值
    loss = (y_pred - y).pow(2).sum().item()
    print(t, loss)

    #反向传播，基于损失函数计算参数w1、w2的梯度
    grad_y_pred = 2.0 * (y_pred - y)
    grad_w2 = h_relu.t().mm(grad_y_pred)
    grad_h_relu = grad_y_pred.mm(w2.t())
    grad_h = grad_h_relu.clone()
    grad_h[h < 0] = 0
    grad_w1 = x.t().mm(grad_h)

    # 使用梯度下降法更新权重参数
    w1 -= learning_rate * grad_w1
    w2 -= learning_rate * grad_w2

# -*- coding: utf-8 -*-

import torch

#定义tensor数据类型

dtype = torch.float

device = torch.device("cpu")

# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y

x = torch.randn(N, D_in, device=device, dtype=dtype)

y = torch.randn(N, D_out, device=device, dtype=dtype)

# 用随机值初始化权重参数

w1 = torch.randn(D_in, H, device=device, dtype=dtype)

w2 = torch.randn(H, D_out, device=device, dtype=dtype)

learning_rate = 1e-6

for t in range(500):

# 前向传播，计算预测值y_pred

h = x.mm(w1)

h_relu = h.clamp(min=0)

y_pred = h_relu.mm(w2)

#计算及打印损失值

loss = (y_pred - y).pow(2).sum().item()

print(t, loss)

#反向传播，基于损失函数计算参数w1、w2的梯度

grad_y_pred = 2.0 * (y_pred - y)

grad_w2 = h_relu.t().mm(grad_y_pred)

grad_h_relu = grad_y_pred.mm(w2.t())

grad_h = grad_h_relu.clone()

grad_h[h < 0] = 0

grad_w1 = x.t().mm(grad_h)

# 使用梯度下降法更新权重参数

w1 -= learning_rate * grad_w1

w2 -= learning_rate * grad_w2

20.3.4利用Tensor和autograd实现自动反向传播

在上面的例子中，我们不得不手动实现神经网络的前向和后向传递。手动实现反向传递对于小型双层网络来说并不是什么大问题，但对于大型复杂网络来说，很快就会变得非常繁琐。
是否有更高效的方法呢？我们可以使用自动微分来自动计算神经网络中的反向传播。 PyTorch中的autograd包提供了这个功能。使用autograd时，网络的正向传递将定义计算图形;图中的节点将是张量，边将是从输入张量产生输出张量的函数。通过此图反向传播，您可以轻松计算梯度。
这听起来很复杂，在实践中使用起来非常简单。每个Tensor代表计算图中的节点。如果x是具有x.requires_grad = True的Tensor，则x.grad是另一个Tensor，相对于某个标量值保持x的梯度。
在这里，我们使用PyTorch Tensors和autograd来实现我们的双层网络;现在我们不再需要手动实现通过网络的反向传播了！

# -*- coding: utf-8 -*-
import torch

#定义tensor的数据类型
dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y的Tensor.
# 这两个Tensors在反向传播时，无需进行梯度，故reqires_grad=False（缺省情况）
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)

# 用随机数生成权重参数w1、w2的Tensors 
# 这两个Tensors在进行反向传播时，需要计算梯度，故设置为requires_grad=True.
w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)
w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)

learning_rate = 1e-6
for t in range(500):
    # 进行正向传播
    #计算预测值y_pred.
    y_pred = x.mm(w1).clamp(min=0).mm(w2)

    #计算损失值.
    # 损失值为一个大小为(1,)的Tensor，即为标签。
    # loss.item() 为损失值.
    loss = (y_pred - y).pow(2).sum()
    print(t, loss.item())

    # 用autograd计算反向传播，这里会根据所有设置了requires_grad=True的Tensor
    # 计算loss的梯度， w1.grad和w2.grad将会保存loss对于w1和w2的梯度
    loss.backward()

    # 手动更新weight，需要用torch.no_grad()，因为weight有required_grad=True
    #但我们不需要在 autograd中跟踪这个操作
    #torch.autograd.no_grad的作用是在上下文环境中切断梯度计算，在此模式下，
    #每一步计算结果中requires_grad都是False，即使input设置为quires_grad=True
    with torch.no_grad():
        w1 -= learning_rate * w1.grad
        w2 -= learning_rate * w2.grad
        # Manually zero the gradients after updating weights
        w1.grad.zero_()
        w2.grad.zero_()

# -*- coding: utf-8 -*-

import torch

#定义tensor的数据类型

dtype = torch.float

device = torch.device("cpu")

# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机数生成输入数据x、目标数据y的Tensor.

# 这两个Tensors在反向传播时，无需进行梯度，故reqires_grad=False（缺省情况）

x = torch.randn(N, D_in, device=device, dtype=dtype)

y = torch.randn(N, D_out, device=device, dtype=dtype)

# 用随机数生成权重参数w1、w2的Tensors

# 这两个Tensors在进行反向传播时，需要计算梯度，故设置为requires_grad=True.

w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)

w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)

learning_rate = 1e-6

for t in range(500):

# 进行正向传播

#计算预测值y_pred.

y_pred = x.mm(w1).clamp(min=0).mm(w2)

#计算损失值.

# 损失值为一个大小为(1,)的Tensor，即为标签。

# loss.item() 为损失值.

loss = (y_pred - y).pow(2).sum()

print(t, loss.item())

# 用autograd计算反向传播，这里会根据所有设置了requires_grad=True的Tensor

# 计算loss的梯度， w1.grad和w2.grad将会保存loss对于w1和w2的梯度

loss.backward()

# 手动更新weight，需要用torch.no_grad()，因为weight有required_grad=True

#但我们不需要在 autograd中跟踪这个操作

#torch.autograd.no_grad的作用是在上下文环境中切断梯度计算，在此模式下，

#每一步计算结果中requires_grad都是False，即使input设置为quires_grad=True

with torch.no_grad():

w1 -= learning_rate * w1.grad

w2 -= learning_rate * w2.grad

# Manually zero the gradients after updating weights

w1.grad.zero_()

w2.grad.zero_()

如果不用with torch.no_grad来更新权重参数，我们可以使用优化器来实现，具体可参考优化器（optim部分）。

20.3.5拓展autograd

我们可以用autograd实现自动反向求导，如果我们想要自己写函数，而又不用自动求导，该如何实现？
实现的方式就是自己定义函数，实现它的正向和反向求导。
在PyTorch中，我们可以通过定义torch.autograd.Function的子类并实现前向和后向函数来轻松定义我们自己的autograd运算符。然后我们可以使用我们的新autograd运算符，通过构造一个实例并像函数一样调用它，传递包含输入数据的Tensors。
在下面例子中，我们定义了自己的自定义autograd函数来执行ReLU，并使用它来实现我们的双层网络：

# -*- coding: utf-8 -*-
import torch

#定义集成torch.autograd.Function的类MyReLU
class MyReLU(torch.autograd.Function):
    """
    通过继承torch.autograd.Function，我们能执行自定义的自动求导函数，而且执行正向和反向传播.
    """
    @staticmethod
    def forward(ctx, input):
    """
        在正向传递中,我们收到一个包含输入和返回输出的张量, ctx是一个上下文对象,可用于存储反向计算的信息.
        您可以使用ctx.save_for_backward方法缓存任意对象以用于反向传播。
        """
        ctx.save_for_backward(input)
        return input.clamp(min=0)

    @staticmethod
    def backward(ctx, grad_output):
        """
        在反向传播中,我们收到一个张量,其中包含相对于输出的损失梯度,
        我们需要计算相关于输入的损失函数梯度。
        """
        input, = ctx.saved_tensors
        grad_input = grad_output.clone()
        grad_input[input < 0] = 0
        return grad_input

dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机值生成输入数据x及目标数据y.
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)

# 初始化权重参数.
w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)
w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)

learning_rate = 1e-6
for t in range(500):
    # 把类MyReLU构造成一个实例relu，便于像函数一样调用。
    relu = MyReLU.apply

    # 正向传播，计算预测值y_pred,这里计算ReLU使用我们自定义的autograd.
    y_pred = relu(x.mm(w1)).mm(w2)

    #计算及打印损失值
    loss = (y_pred - y).pow(2).sum()
    print(t, loss.item())

    # 使用autograd进行反向传播.
    loss.backward()

    # 使用梯度下降法更新权重参数.
    with torch.no_grad():
        w1 -= learning_rate * w1.grad
        w2 -= learning_rate * w2.grad

        # 更新参数后，需要对梯度置为0
        w1.grad.zero_()
        w2.grad.zero_()

# -*- coding: utf-8 -*-

import torch

#定义集成torch.autograd.Function的类MyReLU

class MyReLU(torch.autograd.Function):

"""

通过继承torch.autograd.Function，我们能执行自定义的自动求导函数，而且执行正向和反向传播.

"""

@staticmethod

def forward(ctx, input):

"""

在正向传递中,我们收到一个包含输入和返回输出的张量, ctx是一个上下文对象,可用于存储反向计算的信息.

您可以使用ctx.save_for_backward方法缓存任意对象以用于反向传播。

"""

ctx.save_for_backward(input)

return input.clamp(min=0)

@staticmethod

def backward(ctx, grad_output):

"""

在反向传播中,我们收到一个张量,其中包含相对于输出的损失梯度,

我们需要计算相关于输入的损失函数梯度。

"""

input, = ctx.saved_tensors

grad_input = grad_output.clone()

grad_input[input < 0] = 0

return grad_input

dtype = torch.float

device = torch.device("cpu")

# device = torch.device("cuda:0") # Uncomment this to run on GPU

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 用随机值生成输入数据x及目标数据y.

x = torch.randn(N, D_in, device=device, dtype=dtype)

y = torch.randn(N, D_out, device=device, dtype=dtype)

# 初始化权重参数.

w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)

w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)

learning_rate = 1e-6

for t in range(500):

# 把类MyReLU构造成一个实例relu，便于像函数一样调用。

relu = MyReLU.apply

# 正向传播，计算预测值y_pred,这里计算ReLU使用我们自定义的autograd.

y_pred = relu(x.mm(w1)).mm(w2)

#计算及打印损失值

loss = (y_pred - y).pow(2).sum()

print(t, loss.item())

# 使用autograd进行反向传播.

loss.backward()

# 使用梯度下降法更新权重参数.

with torch.no_grad():

w1 -= learning_rate * w1.grad

w2 -= learning_rate * w2.grad

# 更新参数后，需要对梯度置为0

w1.grad.zero_()

w2.grad.zero_()

【小知识】
Function与Module都可以对pytorch进行自定义拓展，使其满足网络的需求，但这两者还是有十分重要的不同：

（1）Function一般只定义一个操作，因为其无法保存参数，因此适用于激活函数、pooling等操作；Module是保存了参数，因此适合于定义一层，如线性层，卷积层，也适用于定义一个网络
（2）Function需要定义三个方法：__init__, forward, backward（需要自己写求导公式）；Module：只需定义__init__和forward，而backward的计算由自动求导机制构成
（3）可以不严谨的认为，Module是由一系列Function组成，因此其在forward的过程中，Function和Tensor组成了计算图，在backward时，只需调用Function的backward就得到结果，因此Module不需要再定义backward。
（4）Module不仅包括了Function，还包括了对应的参数，以及其他函数与变量，这是Function所不具备的。

20.3.6对比TensorFlow

PyTorch autograd看起来很像TensorFlow：在两个框架中我们定义了一个计算图，并使用自动微分来计算梯度。两者之间最大的区别是TensorFlow的计算图是静态的，PyTorch使用动态计算图。
在TensorFlow中，我们定义计算图一次，然后一遍又一遍地执行相同的图，可能将不同的输入数据提供给图。在PyTorch中，每个前向传递定义了一个新的计算图。
静态图很好，因为你可以预先优化图形;例如，框架可能决定融合某些图形操作以提高效率，或者提出一种策略，用于在多个GPU或许多机器上分布图形。如果您反复使用相同的图表，那么可以分摊这个代价可能高昂的前期优化，因为相同的图表会反复重新运行。
静态和动态图表不同的一个方面是控制流程。对于某些模型，我们可能希望对每个数据点执行不同的计算;例如，可以针对每个数据点针对不同数量的时间步长展开循环网络;这种展开可以作为循环实现。使用静态图形，循环结构需要是图形的一部分;因此，TensorFlow提供了诸如tf.scan之类的运算符，用于将循环嵌入到图中。使用动态图形情况更简单：因为我们为每个示例动态构建图形，我们可以使用常规命令流程控制来执行每个输入不同的计算。
与上面的PyTorch autograd示例相比，这里我们使用TensorFlow来拟合一个简单的双层网：

# -*- coding: utf-8 -*-
import tensorflow as tf
import numpy as np

# 首先设置一个计算图（缺省图）:

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 创建两个占位符，分别用来存放输入数据x和目标值y
#运行计算图时，导入数据.
x = tf.placeholder(tf.float32, shape=(None, D_in))
y = tf.placeholder(tf.float32, shape=(None, D_out))

# 创建权重变量w1和w2，并用随机值初始化.
# TensorFlow 的变量在整个计算图保存其值.
w1 = tf.Variable(tf.random_normal((D_in, H)))
w2 = tf.Variable(tf.random_normal((H, D_out)))

# 前向传播，计算预测值.
# 当前代码并没有实现运行，搭建计算图.
h = tf.matmul(x, w1)
h_relu = tf.maximum(h, tf.zeros(1))
y_pred = tf.matmul(h_relu, w2)

# 计算损失值
loss = tf.reduce_sum((y - y_pred) ** 2.0)

# 计算有关参数w1、w2关于损失函数的梯度.
grad_w1, grad_w2 = tf.gradients(loss, [w1, w2])

#用梯度下降法更新参数. 
# 执行计算图时给 new_w1 和new_w2 赋值
# 对TensorFlow 来说，更新参数是计算图的一部分内容
# 而PyTorch，这部分是属于计算图之外.
learning_rate = 1e-6
new_w1 = w1.assign(w1 - learning_rate * grad_w1)
new_w2 = w2.assign(w2 - learning_rate * grad_w2)

# 已构建计算图, 接下来创建TensorFlow session，准备执行计算图.
with tf.Session() as sess:
    # 执行之前需要初始化变量w1、w2.
    sess.run(tf.global_variables_initializer())

    # 创建numpy多维数组，生成实际输入数据x_value、目标数据 y_value
    x_value = np.random.randn(N, D_in)
    y_value = np.random.randn(N, D_out)
    for _ in range(500):
        # 循环执行计算图. 每次需要把x_value,y_value赋给x和y.
        # 每次执行计算图时，需要计算关于new_w1和new_w2的损失值,
        # 返回numpy多维数组
        loss_value, _, _ = sess.run([loss, new_w1, new_w2],
                                    feed_dict={x: x_value, y: y_value})
        print(loss_value)

# -*- coding: utf-8 -*-

import tensorflow as tf

import numpy as np

# 首先设置一个计算图（缺省图）:

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 创建两个占位符，分别用来存放输入数据x和目标值y

#运行计算图时，导入数据.

x = tf.placeholder(tf.float32, shape=(None, D_in))

y = tf.placeholder(tf.float32, shape=(None, D_out))

# 创建权重变量w1和w2，并用随机值初始化.

# TensorFlow 的变量在整个计算图保存其值.

w1 = tf.Variable(tf.random_normal((D_in, H)))

w2 = tf.Variable(tf.random_normal((H, D_out)))

# 前向传播，计算预测值.

# 当前代码并没有实现运行，搭建计算图.

h = tf.matmul(x, w1)

h_relu = tf.maximum(h, tf.zeros(1))

y_pred = tf.matmul(h_relu, w2)

# 计算损失值

loss = tf.reduce_sum((y - y_pred) ** 2.0)

# 计算有关参数w1、w2关于损失函数的梯度.

grad_w1, grad_w2 = tf.gradients(loss, [w1, w2])

#用梯度下降法更新参数.

# 执行计算图时给 new_w1 和new_w2 赋值

# 对TensorFlow 来说，更新参数是计算图的一部分内容

# 而PyTorch，这部分是属于计算图之外.

learning_rate = 1e-6

new_w1 = w1.assign(w1 - learning_rate * grad_w1)

new_w2 = w2.assign(w2 - learning_rate * grad_w2)

# 已构建计算图, 接下来创建TensorFlow session，准备执行计算图.

with tf.Session() as sess:

# 执行之前需要初始化变量w1、w2.

sess.run(tf.global_variables_initializer())

# 创建numpy多维数组，生成实际输入数据x_value、目标数据 y_value

x_value = np.random.randn(N, D_in)

y_value = np.random.randn(N, D_out)

for _ in range(500):

# 循环执行计算图. 每次需要把x_value,y_value赋给x和y.

# 每次执行计算图时，需要计算关于new_w1和new_w2的损失值,

# 返回numpy多维数组

loss_value, _, _ = sess.run([loss, new_w1, new_w2],

feed_dict={x: x_value, y: y_value})

print(loss_value)

20.3.7高级封装（nn模块）

计算图和autograd是一个非常强大的范例，用于定义复杂的运算符并自动获取导数;然而，对于大型神经网络，原始autograd封装级别较低，需要编写很多代码。
在构建神经网络时，我们经常考虑将计算安排到层中，其中一些层具有可学习的参数，这些参数将在学习期间进行优化。
在TensorFlow中，像Keras，TensorFlow-Slim和TFLearn这样的软件包提供了对构建神经网络有用的原始计算图形的更高级别的抽象。
在PyTorch中也有更高一级的封装，nn包服务于同样的目的。 nn包定义了一组模块，它们大致相当于神经网络层。模块接收输入张量并计算输出张量，但也可以保持内部状态，例如包含可学习参数的张量。 nn包还定义了一组在训练神经网络时常用的有用损失函数。
有关torch.nn的进一步介绍，大家可参考：
http://blog.leanote.com/post/1556905690@qq.com/torch.nn
在这个例子中，我们使用nn包来实现我们的双层网络：

# -*- coding: utf-8 -*-
import torch

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 创建输入、目标数据的Tensor
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

#使用nn包来定义model作为layers 的序列.
# nn.Sequential是一个Module，该Module包含其他Modules(如Linear, ReLU等)
# Sequential Module会序列化的执行这些 Modules, 並且自动计算其output和grads.
#注意因为是序列化执行的, 因此无需自定义 forward. 这是与 nn.Module 的区別之一.
model = torch.nn.Sequential(
    torch.nn.Linear(D_in, H),
    torch.nn.ReLU(),
    torch.nn.Linear(H, D_out),
)

#定义损失函数.
loss_fn = torch.nn.MSELoss(reduction='sum')

learning_rate = 1e-4
for t in range(500):
    #前向传播，计算预测值.
    y_pred = model(x)

    # 计算及打印损失值.
    loss = loss_fn(y_pred, y)
    print(t, loss.item())

    # 进行反向传播前，需要对梯度清零.
    model.zero_grad()

    #反向传播，根据model参数计算损失函数的梯度
    #每个model的 parameters 存放在含requires_grad=True标签的Tensors中
    loss.backward()

    # 利用梯度下降法更新权重参数 .每一个参数都是一个Tensor,并可获取他们的梯度.
    with torch.no_grad():
        for param in model.parameters():
            param -= learning_rate * param.grad

# -*- coding: utf-8 -*-

import torch

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 创建输入、目标数据的Tensor

x = torch.randn(N, D_in)

y = torch.randn(N, D_out)

#使用nn包来定义model作为layers 的序列.

# nn.Sequential是一个Module，该Module包含其他Modules(如Linear, ReLU等)

# Sequential Module会序列化的执行这些 Modules, 並且自动计算其output和grads.

#注意因为是序列化执行的, 因此无需自定义 forward. 这是与 nn.Module 的区別之一.

model = torch.nn.Sequential(

torch.nn.Linear(D_in, H),

torch.nn.ReLU(),

torch.nn.Linear(H, D_out),

)

#定义损失函数.

loss_fn = torch.nn.MSELoss(reduction='sum')

learning_rate = 1e-4

for t in range(500):

#前向传播，计算预测值.

y_pred = model(x)

# 计算及打印损失值.

loss = loss_fn(y_pred, y)

print(t, loss.item())

# 进行反向传播前，需要对梯度清零.

model.zero_grad()

#反向传播，根据model参数计算损失函数的梯度

#每个model的 parameters 存放在含requires_grad=True标签的Tensors中

loss.backward()

# 利用梯度下降法更新权重参数 .每一个参数都是一个Tensor,并可获取他们的梯度.

with torch.no_grad():

for param in model.parameters():

param -= learning_rate * param.grad

20.3.8 优化器（optim）

到目前为止，我们通过手动改变持有可学习参数的Tensors来更新模型的权重（使用torch.no_grad（）或.data以避免在autograd中跟踪历史记录）。对于像随机梯度下降这样的简单优化算法来说，这不是一个巨大的负担，但在实践中，我们经常使用更复杂的优化器如AdaGrad，RMSProp，Adam等来训练神经网络。
PyTorch中的optim包抽象出优化算法的思想，并提供常用优化算法的实现。
在这个例子中，我们将使用nn包像以前一样定义我们的模型，但我们将使用optim包提供的Adam算法优化模型：

# -*- coding: utf-8 -*-
import torch

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 创建随机数据x和目标数据y
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

#使用nn包定义model及损失函数.
model = torch.nn.Sequential(
    torch.nn.Linear(D_in, H),
    torch.nn.ReLU(),
    torch.nn.Linear(H, D_out),
)
loss_fn = torch.nn.MSELoss(reduction='sum')

#使用optim包定义更新模型参数的优化器. 我们选择Adam优化器; optim package
#还包含其他优化算法. Adam的第一个参数为需要更新的Tensors.
learning_rate = 1e-4
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
for t in range(500):
    # 计算预测值.
    y_pred = model(x)

    # 计算打印损失值.
    loss = loss_fn(y_pred, y)
    print(t, loss.item())

    # 反向传播前, 使用优化器对所有需要更新参数的梯度清零
    #这是因为缺省情况下，梯度会存放在缓存里.
    optimizer.zero_grad()

    # 反向传播
    loss.backward()

    #更新参数
    optimizer.step()

# -*- coding: utf-8 -*-

import torch

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 创建随机数据x和目标数据y

x = torch.randn(N, D_in)

y = torch.randn(N, D_out)

#使用nn包定义model及损失函数.

model = torch.nn.Sequential(

torch.nn.Linear(D_in, H),

torch.nn.ReLU(),

torch.nn.Linear(H, D_out),

)

loss_fn = torch.nn.MSELoss(reduction='sum')

#使用optim包定义更新模型参数的优化器. 我们选择Adam优化器; optim package

#还包含其他优化算法. Adam的第一个参数为需要更新的Tensors.

learning_rate = 1e-4

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

for t in range(500):

# 计算预测值.

y_pred = model(x)

# 计算打印损失值.

loss = loss_fn(y_pred, y)

print(t, loss.item())

# 反向传播前, 使用优化器对所有需要更新参数的梯度清零

#这是因为缺省情况下，梯度会存放在缓存里.

optimizer.zero_grad()

# 反向传播

loss.backward()

#更新参数

optimizer.step()

20.3.9 自定义网络层

有时，您需要指定比现有模块序列更复杂的模型; 对于这些情况，您可以通过继承父类nn.Module的方法定义自己的模块，并定义一个接收输入Tensors的forward，并使用其他模块或Tensors上的其他autograd操作生成输出Tensors。
在这个例子中，我们将我们的双层网络实现为自定义Module子类：

# -*- coding: utf-8 -*-
import torch

class TwoLayerNet(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        """
        通常我们將具有引用学习参数的层放在__init__函式中, 將不具有引用学习参数的操作放在forward中。
        """
        super(TwoLayerNet, self).__init__()
        self.linear1 = torch.nn.Linear(D_in, H)
        self.linear2 = torch.nn.Linear(H, D_out)

    def forward(self, x):
        h_relu = self.linear1(x).clamp(min=0)
        y_pred = self.linear2(h_relu)
        return y_pred

# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# 创建输入数据x、目标数据y
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# 实例化类，构建模型
model = TwoLayerNet(D_in, H, D_out)

#构建损失函数及优化器. 其中model.parameters()包含学习参数
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)
for t in range(500):
    # 传入x，计算预测值
    y_pred = model(x)

    # Compute and print loss
    loss = criterion(y_pred, y)
    print(t, loss.item())

    # 对梯度清零，执行反向传播并更新参数.
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

# -*- coding: utf-8 -*-

import torch

class TwoLayerNet(torch.nn.Module):

def __init__(self, D_in, H, D_out):

"""

通常我们將具有引用学习参数的层放在__init__函式中, 將不具有引用学习参数的操作放在forward中。

"""

super(TwoLayerNet, self).__init__()

self.linear1 = torch.nn.Linear(D_in, H)

self.linear2 = torch.nn.Linear(H, D_out)

def forward(self, x):

h_relu = self.linear1(x).clamp(min=0)

y_pred = self.linear2(h_relu)

return y_pred

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# 创建输入数据x、目标数据y

x = torch.randn(N, D_in)

y = torch.randn(N, D_out)

# 实例化类，构建模型

model = TwoLayerNet(D_in, H, D_out)

#构建损失函数及优化器. 其中model.parameters()包含学习参数

criterion = torch.nn.MSELoss(reduction='sum')

optimizer = torch.optim.SGD(model.parameters(), lr=1e-4)

for t in range(500):

# 传入x，计算预测值

y_pred = model(x)

# Compute and print loss

loss = criterion(y_pred, y)

print(t, loss.item())

# 对梯度清零，执行反向传播并更新参数.

optimizer.zero_grad()

loss.backward()

optimizer.step()

20.3.10 控制流与参数共享

作为动态图和权重共享的一个例子，我们实现了一个非常奇怪的模型：一个全连接的ReLU网络，中间会随机选择1到4层隐藏层，重复使用相同的权重多次计算最里面的隐藏层。
对于这个模型，我们可以使用普通的Python流控制来实现循环，并且我们可以通过在定义正向传递时多次重复使用相同的模块来实现最内层之间的权重共享。
我们可以轻松地将此模型实现为Module子类：

# -*- coding: utf-8 -*-
import random
import torch


class DynamicNet(torch.nn.Module):
    def __init__(self, D_in, H, D_out):
        """
        实现三个 nn.Linear 层.
        """
        super(DynamicNet, self).__init__()
        self.input_linear = torch.nn.Linear(D_in, H)
        self.middle_linear = torch.nn.Linear(H, H)
        self.output_linear = torch.nn.Linear(H, D_out)

    def forward(self, x):
        """
        在PyTorch中, 我们可以通过for循环来随机的选择中间层的层数, 使得每一次
执行forward函式时, 都有不同的中间层层数. 而这些中间层都来自于同一个Module例項, 因而具有共享的权重参数.
        """
        h_relu = self.input_linear(x).clamp(min=0)
        for _ in range(random.randint(0, 3)):
            h_relu = self.middle_linear(h_relu).clamp(min=0)
        y_pred = self.output_linear(h_relu)
        return y_pred


# N为输入数据的批量大小; D_in输入数据维度;
# H 为隐含层维度; D_out输出层维度.
N, D_in, H, D_out = 64, 1000, 100, 10

# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)

# Construct our model by instantiating the class defined above
model = DynamicNet(D_in, H, D_out)

# Construct our loss function and an Optimizer. Training this strange model with
# vanilla stochastic gradient descent is tough, so we use momentum
criterion = torch.nn.MSELoss(reduction='sum')
optimizer = torch.optim.SGD(model.parameters(), lr=1e-4, momentum=0.9)
for t in range(500):
    # Forward pass: Compute predicted y by passing x to the model
    y_pred = model(x)

    # Compute and print loss
    loss = criterion(y_pred, y)
    print(t, loss.item())

    # Zero gradients, perform a backward pass, and update the weights.
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

# -*- coding: utf-8 -*-

import random

import torch

class DynamicNet(torch.nn.Module):

def __init__(self, D_in, H, D_out):

"""

实现三个 nn.Linear 层.

"""

super(DynamicNet, self).__init__()

self.input_linear = torch.nn.Linear(D_in, H)

self.middle_linear = torch.nn.Linear(H, H)

self.output_linear = torch.nn.Linear(H, D_out)

def forward(self, x):

"""

在PyTorch中, 我们可以通过for循环来随机的选择中间层的层数, 使得每一次

执行forward函式时, 都有不同的中间层层数. 而这些中间层都来自于同一个Module例項, 因而具有共享的权重参数.

"""

h_relu = self.input_linear(x).clamp(min=0)

for _ in range(random.randint(0, 3)):

h_relu = self.middle_linear(h_relu).clamp(min=0)

y_pred = self.output_linear(h_relu)

return y_pred

# N为输入数据的批量大小; D_in输入数据维度;

# H 为隐含层维度; D_out输出层维度.

N, D_in, H, D_out = 64, 1000, 100, 10

# Create random Tensors to hold inputs and outputs

x = torch.randn(N, D_in)

y = torch.randn(N, D_out)

# Construct our model by instantiating the class defined above

model = DynamicNet(D_in, H, D_out)

# Construct our loss function and an Optimizer. Training this strange model with

# vanilla stochastic gradient descent is tough, so we use momentum

criterion = torch.nn.MSELoss(reduction='sum')

optimizer = torch.optim.SGD(model.parameters(), lr=1e-4, momentum=0.9)

for t in range(500):

# Forward pass: Compute predicted y by passing x to the model

y_pred = model(x)

# Compute and print loss

loss = criterion(y_pred, y)

print(t, loss.item())

# Zero gradients, perform a backward pass, and update the weights.

optimizer.zero_grad()

loss.backward()

optimizer.step()

20.3.11 小试牛刀：用Tensor实现线性回归

本节主要介绍如何利用autograd/Tensor实现线性回归，以此感受autograd的便捷之处。
（1）导入需要的库

import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

import torch as t

%matplotlib inline

from matplotlib import pyplot as plt

from IPython import display

（2）生成输入数据x及目标数据y
设置随机数种子，为了在不同人电脑上运行时下面的输出一致

t.manual_seed(100) 
dtype = t.float
def get_fake_data(batch_size=10):
    ''' 产生随机数据：y = x*2 + 3，加上了一些噪声'''
    x = t.rand(batch_size,1,dtype=dtype) * 20
    y = x * 2 + 3 + t.randn(batch_size, 1)
    return x, y

t.manual_seed(100)

dtype = t.float

def get_fake_data(batch_size=10):

''' 产生随机数据：y = x*2 + 3，加上了一些噪声'''

x = t.rand(batch_size,1,dtype=dtype) * 20

y = x * 2 + 3 + t.randn(batch_size, 1)

return x, y

（3）查看x，y数据分布情况

x, y = get_fake_data()
#squeeze(): 去除size为1的维度,然后转换为numpy数据
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())

x, y = get_fake_data()

#squeeze(): 去除size为1的维度,然后转换为numpy数据

plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())

（4）初始化权重参数

# 随机初始化参数
w = t.randn(1,1, dtype=dtype,requires_grad=True)
b = t.zeros(1,1, dtype=dtype, requires_grad=True)

lr =0.001 # 学习率

# 随机初始化参数

w = t.randn(1,1, dtype=dtype,requires_grad=True)

b = t.zeros(1,1, dtype=dtype, requires_grad=True)

lr =0.001 # 学习率

（5）训练模型

for ii in range(800):
    #x, y = get_fake_data()
       
    # forward：计算loss
    y_pred = x.mm(w) + b.expand_as(y)
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.sum()
    
    # backward：手动计算梯度
    loss.backward()
    
    # 手动更新参数，需要用torch.no_grad()更新参数
    with t.no_grad():
        w -= lr * w.grad
        b -= lr * b.grad
    
    # 梯度清零
        w.grad.zero_()
        b.grad.zero_()
    
    if ii%100 ==0:
        # 画图
        display.clear_output(wait=True)
              
        plt.plot(x.detach().numpy(), y_pred.detach().numpy()) # predicted
        plt.scatter(x.numpy(), y.numpy()) # true data
        
        plt.xlim(0,20)
        plt.ylim(0,41)   
        plt.show()
        plt.pause(0.5)
        
print(w, b)

for ii in range(800):

#x, y = get_fake_data()

# forward：计算loss

y_pred = x.mm(w) + b.expand_as(y)

loss = 0.5 * (y_pred - y) ** 2

loss = loss.sum()

# backward：手动计算梯度

loss.backward()

# 手动更新参数，需要用torch.no_grad()更新参数

with t.no_grad():

w -= lr * w.grad

b -= lr * b.grad

# 梯度清零

w.grad.zero_()

b.grad.zero_()

if ii%100 ==0:

# 画图

display.clear_output(wait=True)

plt.plot(x.detach().numpy(), y_pred.detach().numpy()) # predicted

plt.scatter(x.numpy(), y.numpy()) # true data

plt.xlim(0,20)

plt.ylim(0,41)

plt.show()

plt.pause(0.5)

print(w, b)

运行结果：
tensor([[1.9769]], requires_grad=True) tensor([[3.3058]], requires_grad=True)

20.3.12 小试牛刀：用nn训练CIFAR10

本节使用nn来构建卷积神经网络，采用了nn.Module及nn. functional等模块，因为nn是pytorch的一个较高级的封装，所以整个代码非常简洁，无需考虑很多细节。
（1）CIFAR10数据集简介
CIFAR-10数据集由10类32x32的彩色图片组成，一共包含60000张图片，每一类包含6000图片。其中50000张图片作为训练集，10000张图片作为测试集。
CIFAR-10数据集被划分成了5个训练的batch和1个测试的batch，每个batch均包含10000张图片。测试集batch的图片是从每个类别中随机挑选的1000张图片组成的,训练集batch以随机的顺序包含剩下的50000张图片。不过一些训练集batch可能出现包含某一类图片比其他类的图片数量多的情况。训练集batch包含来自每一类的5000张图片，一共50000张训练图片。下图显示的是数据集的类，以及每一类中随机挑选的10张图片

下载地址：https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
（2）采用LeNet卷积神经网络
LeNet神经网络的结构如下图：

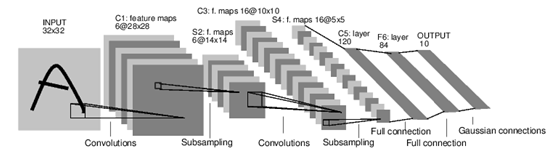
网络结构说明：
①input: 神经网络的输入是一张 32x32 的灰度图像
②conv1: 第一层是一个卷积层，卷积核(kernel size)大小 5x5 ,步长(stride)为 1 ，不进行padding，所以刚才的输入图像，经过这层后会输出6张 28x28 的特征图(feature map)。其中卷积后的大小28，根据(n+2p-f)/s+1得到，n（输入大小）=32，p（填补）=0，f（卷积核大小）=5，s（步幅长度）=1,由此可得：32-5+1=28。
③maxpooling2: 接下来是一个降采样层，用的是maxpooling，stride为 2 , kernel size为 2x2 ，subsampling之后，输出6张 14 x 14的feature map。
④conv3: 第三层又是一个卷积层，kernel size和stride均与第一层相同，不过最后要输出16张feature map。卷积后大小为10,该值根据(n+2p-f)/s+1得到，n（输入大小）=14，p（填补）=0，f（卷积核大小）=5，s（步幅长度）=1,由此可得：14-5+1=10。
⑤maxpooling4:第四层，又是一个maxpooling。
⑥fc5：第五层开始就是全连接(fully connected layer)层，把第四层的feature map摊平，然后做矩阵运算，输出是120个节点。
⑦fc6：输出是84个节点。
⑧output：最后一步是Gaussian Connections，采用了RBF函数（即径向欧式距离函数），计算输入向量和参数向量之间的欧式距离。目前一般采用Softmax。
（3）导入需要的模块

import torch
import torchvision
import torchvision.transforms as transforms

import torch

import torchvision

import torchvision.transforms as transforms

（4）加载数据
利用torchvision可以很方便的加载数据，同时对数据进行规范化处理。

transform = transforms.Compose(
    [transforms.ToTensor(),
     transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                        download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,
                                          shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                       download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=4,
                                         shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',
           'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

transform = transforms.Compose(

[transforms.ToTensor(),

transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])

trainset = torchvision.datasets.CIFAR10(root='./data', train=True,

download=True, transform=transform)

trainloader = torch.utils.data.DataLoader(trainset, batch_size=4,

shuffle=True, num_workers=2)

testset = torchvision.datasets.CIFAR10(root='./data', train=False,

download=True, transform=transform)

testloader = torch.utils.data.DataLoader(testset, batch_size=4,

shuffle=False, num_workers=2)

classes = ('plane', 'car', 'bird', 'cat',

'deer', 'dog', 'frog', 'horse', 'ship', 'truck')

运行结果
Downloading https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz to ./data\cifar-10-python.tar.gz
Files already downloaded and verified
（5）可视化其中部分图形

import matplotlib.pyplot as plt
import numpy as np

ef imshow(img):
    img = img / 2 + 0.5     # unnormalize
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))


# get some random training images
dataiter = iter(trainloader)
images, labels = dataiter.next()

# show images
imshow(torchvision.utils.make_grid(images))
# print labels
print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

import matplotlib.pyplot as plt

import numpy as np

ef imshow(img):

img = img / 2 + 0.5 # unnormalize

npimg = img.numpy()

plt.imshow(np.transpose(npimg, (1, 2, 0)))

# get some random training images

dataiter = iter(trainloader)

images, labels = dataiter.next()

# show images

imshow(torchvision.utils.make_grid(images))

# print labels

print(' '.join('%5s' % classes[labels[j]] for j in range(4)))

运行结果：
cat car car horse

（6）构建网络
需引用学习参数的层放在构造函数__init__中，无需引用学习参数的层放在forward函数中。

import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x


net = Net()

import torch.nn as nn

import torch.nn.functional as F

class Net(nn.Module):

def __init__(self):

super(Net, self).__init__()

self.conv1 = nn.Conv2d(3, 6, 5)

self.pool = nn.MaxPool2d(2, 2)

self.conv2 = nn.Conv2d(6, 16, 5)

self.fc1 = nn.Linear(16 * 5 * 5, 120)

self.fc2 = nn.Linear(120, 84)

self.fc3 = nn.Linear(84, 10)

def forward(self, x):

x = self.pool(F.relu(self.conv1(x)))

x = self.pool(F.relu(self.conv2(x)))

x = x.view(-1, 16 * 5 * 5)

x = F.relu(self.fc1(x))

x = F.relu(self.fc2(x))

x = self.fc3(x)

return x

net = Net()

（7）定义损失函数及优化器

import torch.optim as optim

criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

import torch.optim as optim

criterion = nn.CrossEntropyLoss()

optimizer = optim.SGD(net.parameters(), lr=0.001, momentum=0.9)

（8）训练模型

for epoch in range(2):  # loop over the dataset multiple times

    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        # get the inputs
        inputs, labels = data

        # zero the parameter gradients
        optimizer.zero_grad()

        # forward + backward + optimize
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        # print statistics
        running_loss += loss.item()
        if i % 2000 == 1999:    # print every 2000 mini-batches
            print('[%d, %5d] loss: %.3f' %
                  (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0

print('Finished Training')

for epoch in range(2): # loop over the dataset multiple times

running_loss = 0.0

for i, data in enumerate(trainloader, 0):

# get the inputs

inputs, labels = data

# zero the parameter gradients

optimizer.zero_grad()

# forward + backward + optimize

outputs = net(inputs)

loss = criterion(outputs, labels)

loss.backward()

optimizer.step()

# print statistics

running_loss += loss.item()

if i % 2000 == 1999: # print every 2000 mini-batches

print('[%d, %5d] loss: %.3f' %

(epoch + 1, i + 1, running_loss / 2000))

running_loss = 0.0

print('Finished Training')

运行结果
[1, 2000] loss: 2.192
[1, 4000] loss: 1.840
[1, 6000] loss: 1.672
[1, 8000] loss: 1.565
[1, 10000] loss: 1.511
[1, 12000] loss: 1.473
[2, 2000] loss: 1.387
[2, 4000] loss: 1.345
[2, 6000] loss: 1.330
[2, 8000] loss: 1.299
[2, 10000] loss: 1.304
[2, 12000] loss: 1.266
Finished Training
（9）测试模型
我们已经在训练数据集上循环2次。我们先检查网络是否已经学到了什么。
我们将通过预测神经网络输出的类标签来检查这一点，并根据地面实况进行检查。如果预测正确，我们将样本添加到正确预测列表中。
我们先从测试集中显示一个图像。

dataiter = iter(testloader)
images, labels = dataiter.next()

# print images
imshow(torchvision.utils.make_grid(images))
print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

dataiter = iter(testloader)

images, labels = dataiter.next()

# print images

imshow(torchvision.utils.make_grid(images))

print('GroundTruth: ', ' '.join('%5s' % classes[labels[j]] for j in range(4)))

运行结果
GroundTruth: cat ship ship plane

（10）查看预测结果

outputs = net(images)
_, predicted = torch.max(outputs, 1)

print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(4)))

outputs = net(images)

_, predicted = torch.max(outputs, 1)

print('Predicted: ', ' '.join('%5s' % classes[predicted[j]]

for j in range(4)))

运行结果
Predicted: cat ship ship ship
从这个结果来看，虽然只循环了2次，但4张图片，已识别3张。
接下来我们看在全数据的运行情况。
（11）看神经网络在整个数据集上的表现

correct = 0
total = 0
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (
    100 * correct / total))

correct = 0

total = 0

with torch.no_grad():

for data in testloader:

images, labels = data

outputs = net(images)

_, predicted = torch.max(outputs.data, 1)

total += labels.size(0)

correct += (predicted == labels).sum().item()

print('Accuracy of the network on the 10000 test images: %d %%' % (

100 * correct / total))

运行结果
Accuracy of the network on the 10000 test images: 55 %

（12）查看各类别的性能

class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in testloader:
        images, labels = data
        outputs = net(images)
        _, predicted = torch.max(outputs, 1)
        c = (predicted == labels).squeeze()
        for i in range(4):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1

for i in range(10):
    print('Accuracy of %5s : %2d %%' % (
        classes[i], 100 * class_correct[i] / class_total[i]))

class_correct = list(0. for i in range(10))

class_total = list(0. for i in range(10))

with torch.no_grad():

for data in testloader:

images, labels = data

outputs = net(images)

_, predicted = torch.max(outputs, 1)

c = (predicted == labels).squeeze()

for i in range(4):

label = labels[i]

class_correct[label] += c[i].item()

class_total[label] += 1

for i in range(10):

print('Accuracy of %5s : %2d %%' % (

classes[i], 100 * class_correct[i] / class_total[i]))

运行结果
Accuracy of plane : 52 %
Accuracy of car : 63 %
Accuracy of bird : 35 %
Accuracy of cat : 26 %
Accuracy of deer : 30 %
Accuracy of dog : 50 %
Accuracy of frog : 75 %
Accuracy of horse : 70 %
Accuracy of ship : 77 %
Accuracy of truck : 70 %

（13）GPU上运行
如果在GPU上运行以上网络，可作如下设计

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# Assume that we are on a CUDA machine, then this should print a CUDA device:
print(device)

net.to(device)
inputs, labels = inputs.to(device), labels.to(device)

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

# Assume that we are on a CUDA machine, then this should print a CUDA device:

print(device)

net.to(device)

inputs, labels = inputs.to(device), labels.to(device)

更多pytorch实例可参考：
https://pytorch.org/tutorials/beginner/pytorch_with_examples.html

Python技术交流与分享

分享技术平台

20.1 Pytorch简介

20.2Pytorch安装配置

20.3Pytorch实例

20.3.1利用Numpy实现正向和反向传播（简单实例）

20.3.2利用Numpy实现正向和反向传播（一般情况）

20.3.3Pytorch的Tensor实现正向和反向传播

20.3.4利用Tensor和autograd实现自动反向传播

20.3.5拓展autograd

20.3.6对比TensorFlow

20.3.7高级封装（nn模块）

20.3.8 优化器（optim）

20.3.9 自定义网络层

20.3.10 控制流与参数共享

20.3.11 小试牛刀：用Tensor实现线性回归

20.3.12 小试牛刀：用nn训练CIFAR10