第6章视觉处理基础 | Python技术交流与分享

文章目录

6.1卷积神经网络简介
6.2卷积层
6.2.1 卷积核
6.2.2步幅
6.2.3 填充
6.2.4 多通道上的卷积
6.2.5激活函数
6.2.6卷积函数
6.2.7转置卷积

传统神经网络层之间都采用全连接方式，这种连接方式，如果层数较多，输入又是高维数据，其参数数量可能是一个天文数字。比如训练一张1000*1000像素的灰色图片，输入节点数就是1000*1000，如果隐含层节点是100，那么输入层到隐含层间的权重矩阵就是 1000000*100！如果还要增加隐含层，还要进行反向传播，那结果可想而知。这还不是全部，采用全连接方式还容易导致过拟合。
因此，为更有效处理像图片、视频、音频、自然语言等大数据，必须另辟蹊径。经过多年不懈努力，人们终于找到了一些有效方法或工具。其中卷积神经网络、循环神经网络就是典型代表。接下来我们将介绍卷积神经网络，下一章将介绍循环神经网络。
那卷积神经网络是如何解决天量参数、过拟合等问题的呢？卷积神经网络这么神奇，如何用代码实现？这章就是为解决这些问题而设的，本章主要内容为：
卷积神经网络简介
卷积定义
卷积运算
卷积层
池化层
现代经典网络架构
实例:用TensorFlow实现一个卷积神经网络

6.1卷积神经网络简介

卷积神经网路（Convolutional Neural Network, CNN）是一种前馈神经网络，对于CNN最早可以追溯到1986年BP算法的提出。1989年LeCun将其用到多层神经网络中，直到1998年LeCun提出LeNet-5模型，神经网络的雏形基本形成。在接下来近十年的时间里，卷积神经网络的相关研究处于低谷，原因有两个：一是研究人员意识到多层神经网络在进行BP训练时的计算量极大，当时的硬件计算能力完全不可能实现；二是包括SVM在内的浅层机器学习算法也开始崭露头角。
2006年，Hinton一鸣惊人，在《科学》上发表文章，CNN再度觉醒，并取得长足发展。2012年，ImageNet大赛上CNN夺冠。2014年，谷歌研发出20层的VGG模型。同年，DeepFace、DeepID模型横空出世，直接将LFW数据库上的人脸识别、人脸认证的正确率刷到99.75%，已超越人类平均水平。
卷积神经网路由一个或多个卷积层和顶端的全连通层（对应经典的神经网路）组成，同时也包括关联权重和池化层（pooling layer）等。图6-1就是一个卷积神经网络架构。

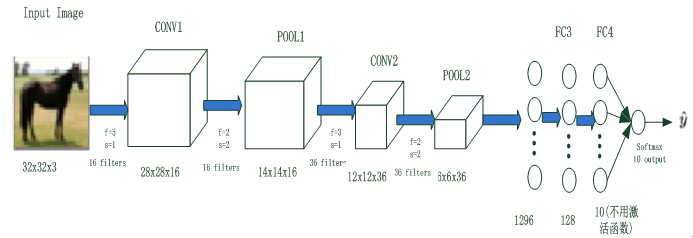
图6-1 卷积神经网络示意图
与其他深度学习结构相比，卷积神经网路在图像和语音识别方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比其他深度、前馈神经网路，卷积神经网路用更少参数，却能获得更高性能。
图6-1为卷积神经网络的一般结构，其中包括卷积神经网络的常用层，如卷积层、池化层、全连接层和输出层；有些还包括其他层，如正则化层、高级层等。接下来我们就各层的结构、原理等进行详细说明。
图6-1是用一个比较简单的卷积神经网络对手写输入数据进行分类，由卷积层(Conv2d)、池化层(MaxPool2d)和全连接层(Linear)叠加而成。下面我们先用代码定义这个卷积神经网络，然后，介绍各部分的定义及原理。

import torch.nn as nn
import torch.nn.functional as F
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

class CNNNet(nn.Module):
    def __init__(self):
        super(CNNNet,self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3,out_channels=16,kernel_size=5,stride=1)
        self.pool1 = nn.MaxPool2d(kernel_size=2,stride=2)
        self.conv2 = nn.Conv2d(in_channels=16,out_channels=36,kernel_size=3,stride=1)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
        self.fc1 = nn.Linear(1296,128)
        self.fc2 = nn.Linear(128,10)      

    def forward(self,x):
        x=self.pool1(F.relu(self.conv1(x)))
        x=self.pool2(F.relu(self.conv2(x)))
        #print(x.shape)
        x=x.view(-1,36*6*6)
        x=F.relu(self.fc2(F.relu(self.fc1(x))))
        return x

net = CNNNet()
net=net.to(device)

import torch.nn as nn

import torch.nn.functional as F

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")

class CNNNet(nn.Module):

def __init__(self):

super(CNNNet,self).__init__()

self.conv1 = nn.Conv2d(in_channels=3,out_channels=16,kernel_size=5,stride=1)

self.pool1 = nn.MaxPool2d(kernel_size=2,stride=2)

self.conv2 = nn.Conv2d(in_channels=16,out_channels=36,kernel_size=3,stride=1)

self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)

self.fc1 = nn.Linear(1296,128)

self.fc2 = nn.Linear(128,10)

def forward(self,x):

x=self.pool1(F.relu(self.conv1(x)))

x=self.pool2(F.relu(self.conv2(x)))

#print(x.shape)

x=x.view(-1,36*6*6)

x=F.relu(self.fc2(F.relu(self.fc1(x))))

return x

net = CNNNet()

net=net.to(device)

6.2卷积层

卷积层是卷积神经网络的核心层，而卷积（Convolution）又是卷积层的核心。卷积我们直观的理解，就是两个函数的一种运算，这种运算称为卷积运算。这样说或许比较抽象，我们还是先抛开复杂概念，先从具体实例开始吧。图6-2 就是一个简单的二维空间卷积运算示例，虽然简单，但却包含了卷积的核心内容。

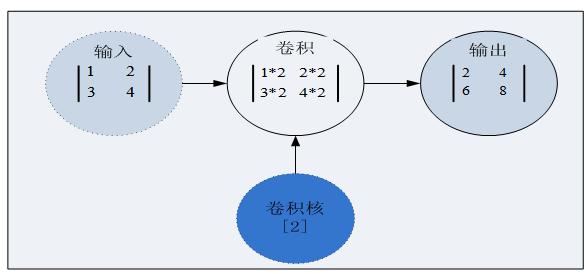
图6-2 在二维空间上的一个卷积运算
在图6-2中，输入和卷积核都是张量，卷积运算就是用卷积分别乘以输入张量中的每个元素，然后输出一个代表每个输入信息的张量。其中卷积核（kernel）又称为权重过滤器或简称过滤器（filter）。接下来我们把输入、卷积核推广到更高维空间上，输入由2x2矩阵，拓展为5x5矩阵，卷积核由一个标量拓展为一个3x3矩阵，如图6-3。这时该如何进行卷积呢？

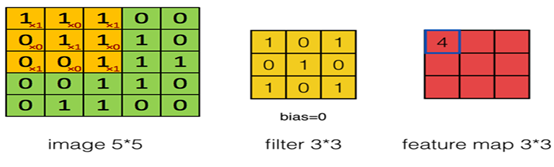
图6-3 卷积神经网络卷积运算，生成右边矩阵中第1行第1列的数据
用卷积核中每个元素，乘以对应输入矩阵中的对应元素，这点还是一样，但输入张量为5x5矩阵，而卷积核为3x3矩阵，所以这里首先就要解决一个如何对应的问题,这个问题解决了，这个推广也就完成了。把卷积核作为在输入矩阵上一个移动窗口，对应关系就迎刃而解。
卷积核如何确定？卷积核如何在输入矩阵中移动？移动过程中出现超越边界如何处理？这种因移动可能带来的问题，接下来将进行说明。

6.2.1 卷积核

卷积核，从这个名字可以看出它的重要性，它是整个卷积过程的核心。比较简单的卷积核或过滤器有Horizontalfilter、Verticalfilter、Sobel filter等。这些过滤器能够检测图像的水平边缘、垂直边缘、增强图片中心区域权重等。过滤器的具体作用，我们通过以下一些图来说明。
（1）垂直边缘检测

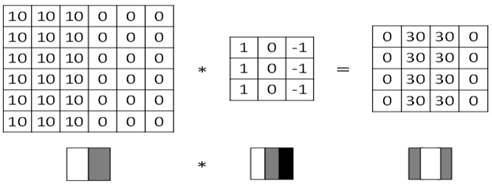
图6-4 过滤器对垂直边缘的检测
这个过滤器是3x3矩阵（注，过滤器一般是奇数阶矩阵），其特点是有值的是第1列和第3列，第2列为0。经过这个过滤器作用后，就把原数据垂直边缘检测出来了。
（2）水平边缘检测

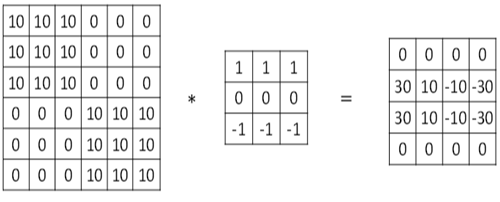
图6-5 水平过滤器检测水平边缘示意图
这个过滤器也是3x3矩阵，其特点是有值的是第1行和第3行，第2行为0。经过这个过滤器作用后，就把原数据水平边缘检测出来了。
（3）过滤器对图像水平边缘检测、垂直边缘检测的效果图

图6-6过滤器对图像水平边缘检测、垂直边缘检测后的效果图
以上这些过滤器是比较简单的，在深度学习中，过滤器的作用不仅在于检测垂直边缘、水平边缘等，还需要检测其他边缘特征。
过滤器如何确定呢？过滤器类似于标准神经网络中的权重矩阵W，W需要通过梯度下降算法反复迭代求得。同样，在深度学习学习中，过滤器也是需要通过模型训练来得到。卷积神经网络主要目的就是计算出这些filter的数值。确定得到了这些filter后，卷积神经网络的浅层网络也就实现了对图片所有边缘特征的检测。
这节简单说明了卷积核的生成方式及作用。假设卷积核已确定，卷积核如何对输入数据进行卷积运算呢？这将在下节进行介绍。

6.2.2步幅

如何实现对输入数据进行卷积运算？回答这个问题之前，我们先回顾一下图6-3。在图6-3的左边的窗口中，左上方有个小窗口，这个小窗口实际上就是卷积核，其中x后面的值就是卷积核的值。如第1行为：x1、x0、x1对应卷积核的第1行[1 0 1]。右边窗口中这个4是如何得到的呢？就是5x5矩阵中由前3行、前3列构成的矩阵各元素乘以卷积核中对应位置的值，然后累加得到的。即：1x1+1x0+1x1+0x0+1x1+1x0+0x1+0x0+1x1=4,右边矩阵中第1行第2列的值如何得到呢？我们只要把左图中小窗口往右移动一格，然后，进行卷积运算；第1行第3列，如此类推；第2行、第3行的值，只要把左边的小窗口往下移动一格，然后再往右即可。看到这里，如果还不很清楚，没关系，看图6-7就一目了然。

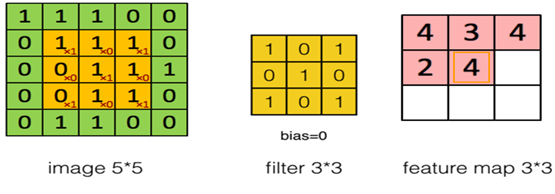
图6-7卷积神经网络卷积运算，生成右边矩阵中第2行第2列的数据
小窗口（实际上就是卷积核或过滤器）在左边窗口中每次移动的格数（无论是自左向右移动，或自上向下移动）称为步幅(strides),在图像中就是跳过的像素个数。上面小窗口每次只移动一格，故参数strides=1。这个参数也可以是2或3等数。如果是2，每次移动时就跳2格或2个像素，如下图6-8所示。

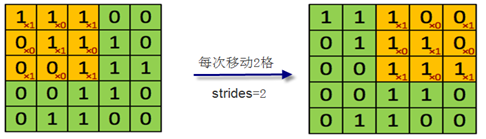
图6-8 strides=2 示意图
在小窗口移动过程中，其值始终是不变的，都是卷积核的值。换一句话来说，卷积核的值，在整个过程中都是共享的，所以又把卷积核的值称为共享变量。卷积神经网络采用参数共享的方法大大降低了参数的数量。
参数strides是卷积神经网络中的一个重要参数，在用PyTorch具体实现时，strides参数格式为单个整数或两个整数的元组（分别表示在height和width维度上的值）。
在图6-8中，小窗口如果继续往右移动2格，卷积核窗口部分在输入矩阵之外，如下图6-9。此时，该如何处理呢？具体处理方法就涉及到下节要讲的内容--填充(padding)。

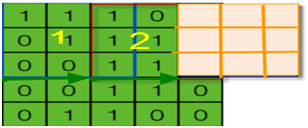
图6-9小窗口移动输入矩阵外

6.2.3 填充

当输入图片与卷积核不匹配时或卷积核超过图片边界时，可以采用边界填充（padding）的方法。即把图片尺寸进行扩展，扩展区域补零。如图6-10。当然也可不扩展。

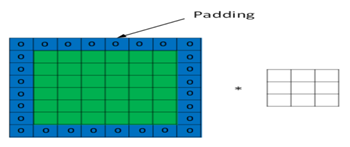
图6-10采用padding方法，对图片进行扩展，然后补零。
根据是否扩展padding又分为Same、Valid。采用Same方式时，对图片扩展并补0；采用Valid方式时，对图片不扩展。如何选择呢？在实际训练过程中，一般选择Same，使用Same不会丢失信息。设补0的圈数为p，输入数据大小为n，过滤器大小为f，步幅大小为s，则有：

6.2.4 多通道上的卷积

前面我们对卷积在输入数据、卷积核的维度上进行了扩展，但输入数据、卷积核都是单个，如果从图形的角度来说都是灰色的，没有考虑彩色图片情况。在实际应用中，输入数据往往是多通道的，如彩色图片就3通道，即R、G、B通道。对于3通道的情况如何卷积呢？3通道图片的卷积运算与单通道图片的卷积运算基本一致，对于3通道的RGB图片，其对应的滤波器算子同样也是3通道的。例如一个图片是6 x 6 x 3，分别表示图片的高度（height）、宽度（weight）和通道（channel）。过程是将每个单通道（R，G，B）与对应的filter进行卷积运算求和，然后再将3通道的和相加，得到输出图片的一个像素值。具体过程如图6-11所示。

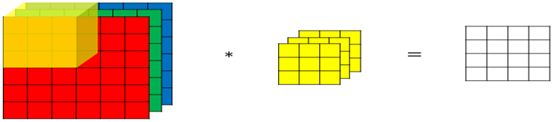
图6-11 3通道卷积示意图
为了实现更多边缘检测，可以增加更多的滤波器组。图6-12就是两组过滤器Filter W0和Filter W1。7*7*3输入，经过两个3*3*3的卷积(步幅为2)，得到了3*3*2的输出。另外我们也会看到图6-10中的Zero padding是1，也就是在输入元素的周围补了一圈0。Zero padding对于图像边缘部分的特征提取是很有帮助的，可以防止信息丢失。最后，不同滤波器组卷积得到不同的输出，个数由滤波器组决定。

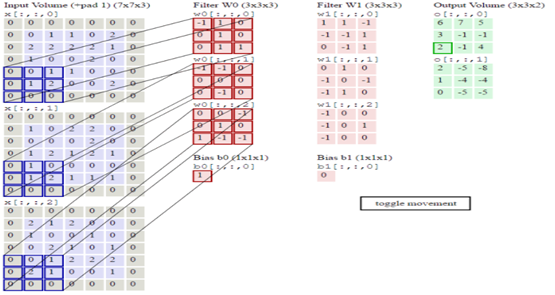
图6-12多组卷积核的卷积运算示意图

6.2.5激活函数

卷积神经网络与标准的神经网络类似，为保证其非线性，也需要使用激活函数，即在卷积运算后，把输出值另加偏移量，输入到激活函数，然后作为下一层的输入，如图6-13所示。

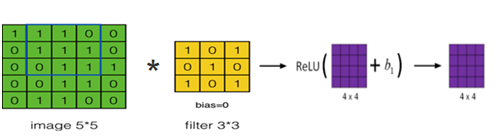
图6-13卷积运算后的结果+偏移量输入到激活函数ReLU
常用的激活函数有：tf.sigmoid、tf.nn.relu 、tf.tanh、 tf.nn.dropout等，这些激活函数的详细介绍可参考本书第5章。

6.2.6卷积函数

卷积函数是构建神经网络的重要支架，通常Pytorch的卷积运算是通过nn.Conv2d来完成。下面先介绍nn.Conv2d的参数，及如何计算输出的形状(shape)。
(1) nn.Conv2d函数

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')

1	torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros')

主要参数说明：
in_channels(int)
输入信号的通道
out_channels(int)
卷积产生的通道
kerner_size(int or tuple)
卷积核的尺寸
stride(int or tuple, optional)
卷积步长
padding(int or tuple, optional)
输入的每一条边补充0的层数
dilation(int or tuple, optional)
卷积核元素之间的间距
groups(int, optional)
控制输入和输出之间的连接： group=1，输出是所有的输入的卷积；group=2，此时相当于有并排的两个卷积层，每个卷积层计算输入通道的一半，并且产生的输出是输出通道的一半，随后将这两个输出连接起来。
bias(bool, optional)
如果bias=True，添加偏置。其中参数kernel_size，stride,padding，dilation也可以是一个int的数据，此时卷积height和width值相同;也可以是一个tuple数组，tuple的第一维度表示height的数值，tuple的第二维度表示width的数值
(2)输出形状

当groups=1时

conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=1)
conv.weight.data.size()  # torch.Size([12, 6, 1, 1])

1 2	conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=1) conv.weight.data.size() # torch.Size([12, 6, 1, 1])

当groups=2时

conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=2)
conv.weight.data.size() #torch.Size([12, 3, 1, 1])

1 2	conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=2) conv.weight.data.size() #torch.Size([12, 3, 1, 1])

当groups=3时

conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=3)
conv.weight.data.size() #torch.Size([12, 2, 1, 1])

1 2	conv = nn.Conv2d(in_channels=6, out_channels=12, kernel_size=1, groups=3) conv.weight.data.size() #torch.Size([12, 2, 1, 1])

in_channels/groups必须是整数，否则报错。

6.2.7转置卷积

转置卷积(Transposed Convolution)在一些文献中也称之为反卷积(Deconvolution)或部分跨越卷积(Fractionally-strided Convolution)。何为转置卷积，它与卷积又有哪些不同？
通过卷积的正向传播的图像一般越来越小，是下采样（downsampled）。卷积的方向传播实际上就是一种转置卷积，它是上采样（up-sampling）。
我们先简单回顾卷积的正向传播是如何运算的，假设卷积操作的相关参数为：输入大小为4，卷积核大小为3，步幅为2，填充为0，即 (n=4,f=3,s=1,p=0)，根据公式（6.2）可知，输出 o=2。
整个卷积过程，可用图6-14 表示：

图6-14 卷积运算示意图
对于上述卷积运算，我们把图6-14所示的3×3卷积核展成一个如下所示的[4,16]的稀疏矩阵 C，其中非0元素 ωi,j 表示卷积核的第 i 行和第 j 列。

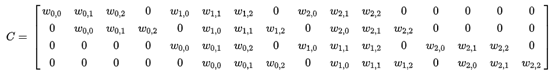
我们再把4×4的输入特征展成[16,1]的矩阵 X，那么 Y=CX 则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出，卷积层的计算其实是可以转化成矩阵相乘。
反向传播时又会如何呢？首先从卷积的反向传播算法开始。假设损失函数为L，则反向传播时，对L关系的求导，利用链式法则得到：

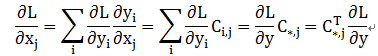
由此，可得X=C^T Y ，即反卷积的操作就是要对这个矩阵运算过程进行逆运算。
转置卷积在生成式对抗网络(GAN)中使用很普遍，后续我们将介绍，图6-15为使用转置卷积的一个示例，它一个上采样过程。

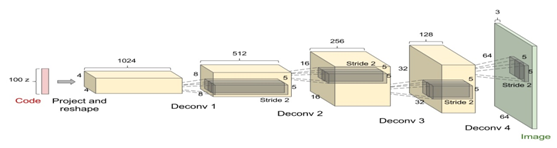
图6-15 转置卷积示例
Pytorch二维转置卷积的格式为：

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')

1	torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros')

待续.............