第8章生成式深度学习 | Python技术交流与分享

文章目录

8.1 用变分自编码器生成图像
8.1.1 自编码器
8.1.2变分自编码器
8.1.3用变分自编码器生成图像
8.2 GAN简介
8.2.1 GAN架构
8.2.2 GAN的损失函数
8.3用GAN生成图像
8.3.1判别器
8.3.2 生成器
8.3.3 训练模型
8.3.4 可视化结果
8.4 VAE与GAN的异同

深度学习不仅在于其强大的学习能力，更在于它的创新能力。我们通过构建判别模型来提升模型的学习能力，通过构建生成模型来发挥其创新能力。判别模型通常利用训练样本训练模型,然后利用该模型，对新样本x，进行判别或预测。而生成模型正好反过来，根据一些规则y，来生成新样本x。
生成式模型很多，本章主要介绍常用的两种：变分自动编码器(VAE)和生成式对抗网络(GAN)及其变种。虽然两者都是生成模型，并且通过各自的生成能力展现其强大的创新能力，但他们在具体实现上有所不同。GAN基于博弈论，目的是找到达到纳什均衡的判别器网络和生成器网络。而VAE基本根植贝叶斯推理，其目标是潜在地建模，从模型中采样新的数据。
本章主要介绍多种生成式网络，具体内容如下：
用变分自编码器生成图像
GAN简介
如何用GAN生成图像
比较VAE与GAN的异同
CGAN、DCGAN简介

8.1 用变分自编码器生成图像

变分自编码器是自编码器的改进版本，自编码器是一种无监督学习，但它无法产生新的内容，变分自编码器对其潜在空间进行拓展，使其满足正态分布，情况就大不一样了。

8.1.1 自编码器

自编码器是通过对输入X进行编码后得到一个低维的向量z，然后根据这个向量还原出输入X。通过对比X与X ̃的误差，再利用神经网络去训练使得误差逐渐减小，从而达到非监督学习的目的。图8-1 为自编码器的架构图:

图8-1 自编码器架构图
自编码器因不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。为解决这一问题，人们对潜在空间Z（潜在变量对应的空间）增加一些约束，使Z满足正态分布，由此就出现了VAE模型，VAE对编码器添加约束，就是强迫它产生服从单位正态分布的潜在变量。正是这种约束，把VAE和自编码器区分开来。

8.1.2变分自编码器

变分自编码器关键一点就是增加一个对潜在空间Z的正态分布约束，如何确定这个正态分布就成主要目标，我们知道要确定正态分布，只要确定其两个参数均值u和标准差σ。那么如何确定u、σ？用一般的方法或估计比较麻烦效果也不好，人们发现用神经网络去拟合，简单效果也不错。图8-2 为AVE的架构图。

图8-2 AVE架构图
在图8-2中，模块①的功能把输入样本X通过编码器输出两个m维向量（mu、log_var）,这两个向量是潜在空间（假设满足正态分布）的两个参数（相当于均值和方差）。那么如何从这个潜在空间采用一个点Z?
这里假设潜在正态分布能生成输入图像，从标准正态分布N(0,I)中采样一个ε（模块②的功能），然后使
Z=mu+ exp⁡(log_var)*ε （8.1）
这也是模块③的主要功能。
Z是从潜在空间抽取的一个向量，Z通过解码器生成一个样本X ̃，这是模块④的功能。
这里ε是随机采样的，这就可保证潜在空间的连续性、良好的结构性。而这些特性使得潜在空间的每个方向都表示数据中有意义的变化方向。
以上这些步骤构成整个网络的前向传播过程，反向传播如何进行？要确定反向传播就涉及到损失函数了，损失函数是衡量模型优劣的主要指标。这里我们需要从以下两个方面进行衡量。
（1）生成的新图像与原图像的相似度；
（2）隐含空间的分布与正态分布的相似度。
度量图像的相似度一般采用交叉熵(如nn.BCELoss)，度量两个分布的相似度一般采用KL散度(Kullback-Leibler divergence)。这两个度量的和构成了整个模型的损失函数。
以下是损失函数的具体代码，AVE损失函数的推导过程，有兴趣的读者可参考原论文：https://arxiv.org/pdf/1606.05908.pdf

# 定义重构损失函数及KL散度
reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
#两者相加得总损失
loss= reconst_loss+ kl_div

# 定义重构损失函数及KL散度

reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)

kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

#两者相加得总损失

loss= reconst_loss+ kl_div

8.1.3用变分自编码器生成图像

前面我们介绍了AVE的架构和原理，至此对AVE的“蓝图”就有了大致了解，如何实现这个蓝图？这节我们将结合代码，用Pytorch实现AVE。此外，还包括在实现过程中需要注意的一些问题，为便于说明起见，数据集采用MNIST,整个网络结构如图8-3所示。

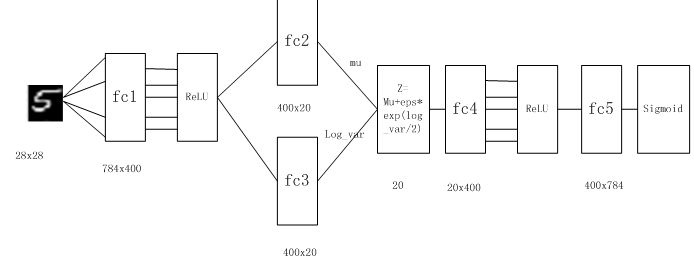
图8-3 AVE网络结构图
首先，我们简单介绍一下实现的具体步骤，然后，结合代码详细说明，如何用Pytorch一步步实现AVE。具体步骤如下：
（1）导入必要的包

import os
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import transforms
from torchvision.utils import save_image

import os

import torch

import torch.nn as nn

import torch.nn.functional as F

import torchvision

from torchvision import transforms

from torchvision.utils import save_image

（2）定义一些超参数

image_size = 784
h_dim = 400
z_dim = 20
num_epochs = 30
batch_size = 128
learning_rate = 0.001

image_size = 784

h_dim = 400

z_dim = 20

num_epochs = 30

batch_size = 128

learning_rate = 0.001

（3）对数据集进行预处理，如转换为Tensor，把数据集转换为循环、可批量加载的数据集；

# 下载MNIST训练集，这里因已下载，故download=False
# 如果需要下载，设置download=True将自动下载
dataset = torchvision.datasets.MNIST(root='data',
                                     train=True,
                                     transform=transforms.ToTensor(),
                                     download=False)

#数据加载
data_loader = torch.utils.data.DataLoader(dataset=dataset,
                                          batch_size=batch_size, 
                                          shuffle=True)

# 下载MNIST训练集，这里因已下载，故download=False

# 如果需要下载，设置download=True将自动下载

dataset = torchvision.datasets.MNIST(root='data',

train=True,

transform=transforms.ToTensor(),

download=False)

#数据加载

data_loader = torch.utils.data.DataLoader(dataset=dataset,

batch_size=batch_size,

shuffle=True)

（4）构建AVE模型，主要由encode和decode两部分组成；

# 定义AVE模型
class VAE(nn.Module):
    def __init__(self, image_size=784, h_dim=400, z_dim=20):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, h_dim)
        self.fc2 = nn.Linear(h_dim, z_dim)
        self.fc3 = nn.Linear(h_dim, z_dim)
        self.fc4 = nn.Linear(z_dim, h_dim)
        self.fc5 = nn.Linear(h_dim, image_size)
        
    def encode(self, x):
        h = F.relu(self.fc1(x))
        return self.fc2(h), self.fc3(h)
    
    #用mu，log_var生成一个潜在空间点z，mu，log_var为两个统计参数，我们假设
    #这个假设分布能生成图像。
    def reparameterize(self, mu, log_var):
        std = torch.exp(log_var/2)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        h = F.relu(self.fc4(z))
        return F.sigmoid(self.fc5(h))
    
    def forward(self, x):
        mu, log_var = self.encode(x)
        z = self.reparameterize(mu, log_var)
        x_reconst = self.decode(z)
        return x_reconst, mu, log_var

# 定义AVE模型

class VAE(nn.Module):

def __init__(self, image_size=784, h_dim=400, z_dim=20):

super(VAE, self).__init__()

self.fc1 = nn.Linear(image_size, h_dim)

self.fc2 = nn.Linear(h_dim, z_dim)

self.fc3 = nn.Linear(h_dim, z_dim)

self.fc4 = nn.Linear(z_dim, h_dim)

self.fc5 = nn.Linear(h_dim, image_size)

def encode(self, x):

h = F.relu(self.fc1(x))

return self.fc2(h), self.fc3(h)

#用mu，log_var生成一个潜在空间点z，mu，log_var为两个统计参数，我们假设

#这个假设分布能生成图像。

def reparameterize(self, mu, log_var):

std = torch.exp(log_var/2)

eps = torch.randn_like(std)

return mu + eps * std

def decode(self, z):

h = F.relu(self.fc4(z))

return F.sigmoid(self.fc5(h))

def forward(self, x):

mu, log_var = self.encode(x)

z = self.reparameterize(mu, log_var)

x_reconst = self.decode(z)

return x_reconst, mu, log_var

（5）选择GPU及优化器

# 设置pytorch在哪块GPU上运行，这里假设使用序号为1的这块GPU.
torch.cuda.set_device(1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# 设置pytorch在哪块GPU上运行，这里假设使用序号为1的这块GPU.

torch.cuda.set_device(1)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

model = VAE().to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

（6）训练模型，同时保存原图像与随机生成的图像；

with torch.no_grad():
        # 保存采样图像，即潜在向量Z通过解码器生成的新图像
        z = torch.randn(batch_size, z_dim).to(device)
        out = model.decode(z).view(-1, 1, 28, 28)
        save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

        # 保存重构图像，即原图像通过解码器生成的图像
        out, _, _ = model(x)
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
        save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

with torch.no_grad():

# 保存采样图像，即潜在向量Z通过解码器生成的新图像

z = torch.randn(batch_size, z_dim).to(device)

out = model.decode(z).view(-1, 1, 28, 28)

save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

# 保存重构图像，即原图像通过解码器生成的图像

out, _, _ = model(x)

x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)

save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

（7）展示原图像及重构图像

reconsPath = './ave_samples/reconst-30.png'
Image = mpimg.imread(reconsPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

reconsPath = './ave_samples/reconst-30.png'

Image = mpimg.imread(reconsPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

这是迭代30次的结果

图8-4 AVE构建图片
图8-4中，奇数列为原图像，偶数列为原图像重构的图像。从这个结果可以看出重构图像效果还不错。图8-5为由潜在空间通过解码器生成的新图像，这个图像效果也不错。
（8）显示由潜在空间点Z生成的新图像

genPath = './ave_samples/sampled-30.png'
Image = mpimg.imread(genPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

genPath = './ave_samples/sampled-30.png'

Image = mpimg.imread(genPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

图8-5 AVE新图片
这里构建网络主要用全连接层，有兴趣的读者，可以把卷积层，如果编码层使用卷积层(如nn.Conv2d)，解码器需要使用反卷积层(nn. ConvTranspose2d)。接下来我们介绍生成式对抗网络，并用该网络生成新数字，其效果将好于AVE生成的数字。

8.2 GAN简介

上节我们介绍了基于自动编码器的AVE，根据这个网络可以生成新的图像。这节我们将介绍另一种生成式网络，它是基于博弈论的，所以又称为生成式对抗网络（Generative adversarial nets，GAN）。它是2014年由Ian Goodfellow提出的，它要解决的问题是如何从训练样本中学习出新样本，训练样本是图片就生成新图片，训练样本是文章就输出新文章等等。
GAN既不依赖标签来优化，也不是根据对结果奖惩来调整参数。它是依据生成器和判别器之间的博弈来不断优化。打个不一定很恰当的比喻，就像一台验钞机和一台制造假币的机器之间的博弈，两者不断博弈，博弈的结果假币越来越像真币，直到验钞机无法识别一张货币是假币还是真币为止。这样说，还是有点抽象，接下来我们将从多个侧面进行说明。

8.2.1 GAN架构

VAE利用潜在空间，可以生成连续的新图像，不过因损失函数采用像素间的距离，所以图像有点模糊。能否生成更清晰的新图像呢？可以的，这里我们用GAN替换VAE的潜在空间，它能够迫使生成图像与真实图像在统计上几乎无法区别的逼真合成图像。
GAN的直观理解，可以想象一个名画伪造者想伪造一幅达芬奇的画作，开始时，伪造者技术不精，但他，将自己的一些赝品和达芬奇的作品混在一起，请一个艺术商人对每一幅画进行真实性评估，并向伪造者反馈，告诉他哪些看起来像真迹、哪些看起来不像真迹。
伪造者根据这些反馈，改进自己的赝品。随着时间的推移，伪造者技能越来越高，艺术商人也变得越来越擅长找出赝品。最后，他们手上就拥有了一些非常逼真的赝品。
这就是GAN的基本原理。这里有两个角色，一个是伪造者，另一个是技术鉴赏者。他们训练的目的都是打败对方。
因此，GAN从网络的角度来看，它由两部分组成。
（1）生成器网络：它一个潜在空间的随机向量作为输入，并将其解码为一张合成图像。
（2）判别器网络：以一张图像（真实的或合成的均可）作为输入，并预测该图像来自训练集还是来自生成器网络。图8-6 为其架构图。

图8-6 GAN架构图
如何不断提升判别器辨别是非的能力？如何使生成的图片越来越像真图片？这些都通过控制它们各自的损失函数来控制。
训练结束后，生成器能够将输入空间中的任何点转换为一张可信图像。与VAE不同的是，这个潜空间无法保证带连续性或有特殊含义的结构。
GAN的优化过程不像通常的求损失函数的最小值，而是保持生成与判别两股力量的动态平衡。因此，其训练过程要比一般神经网络难很多。

8.2.2 GAN的损失函数

从GAN的架构图(图8-6)可知，控制生成器或判别器的关键是损失函数，如何定义损失函数成为整个GAN的关键。我们的目标很明确，既要不断提升判断器辨别是非或真假的能力，又要不断提升生成器不断提升图片质量，使判别器越来越难判别。这些目标如何用程序体现？损失函数就能充分说明。
为了达到判别器的目标，其损失函数既要考虑识别真图片能力，又要考虑识别假图片能力，而不能只考虑一方面，故判别器的损失函数为两者的和，具体代码如下：
D表示判别器，G为生成器，real_labels，fake_labels分别表示真图片标签、假图片标签。images是真图片，z是从潜在空间随机采样的向量，通过生成器得到假图片。

# 定义判断器对真图片的损失函数
outputs = D(images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
        
# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs            
# 得到判别器总的损失函数
d_loss = d_loss_real + d_loss_fake

# 定义判断器对真图片的损失函数

outputs = D(images)

d_loss_real = criterion(outputs, real_labels)

real_score = outputs

# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

d_loss_fake = criterion(outputs, fake_labels)

fake_score = outputs

# 得到判别器总的损失函数

d_loss = d_loss_real + d_loss_fake

生成器的损失函数如何定义，才能使其越来越向真图片靠近？以真图片为标杆或标签即可。具体代码如下：

z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)        
        
g_loss = criterion(outputs, real_labels)

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

g_loss = criterion(outputs, real_labels)

8.3用GAN生成图像

为便于说明GAN的关键环节，这里我们弱化了网络和数据集的复杂度。数据集为MNIST、网络用全连接层。后续我们将用一些卷积层的实例来说明。

8.3.1判别器

获取数据，导入模块基本与AVE的类似，这里就不展开来说，详细内容大家可参考char-08代码模块。
定义判别器网络结构，这里使用LeakyReLU为激活函数，输出一个节点并经过Sigmoid后输出，用于真假二分类。

# 构建判断器
D = nn.Sequential(
    nn.Linear(image_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, 1),
    nn.Sigmoid())

# 构建判断器

D = nn.Sequential(

nn.Linear(image_size, hidden_size),

nn.LeakyReLU(0.2),

nn.Linear(hidden_size, hidden_size),

nn.LeakyReLU(0.2),

nn.Linear(hidden_size, 1),

nn.Sigmoid())

8.3.2 生成器

生成器与AVE的生成器类似，不同的地方是输出为nn.tanh,使用nn.tanh将使数据分布在[-1,1]之间。其输入是潜在空间的向量z，输出维度与真图片相同。

# 构建生成器，这个相当于AVE中的解码器 
G = nn.Sequential(
    nn.Linear(latent_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, image_size),
    nn.Tanh())

# 构建生成器，这个相当于AVE中的解码器

G = nn.Sequential(

nn.Linear(latent_size, hidden_size),

nn.ReLU(),

nn.Linear(hidden_size, hidden_size),

nn.ReLU(),

nn.Linear(hidden_size, image_size),

nn.Tanh())

8.3.3 训练模型

for epoch in range(num_epochs):
    for i, (images, _) in enumerate(data_loader):
        images = images.reshape(batch_size, -1).to(device)
        
        # 定义图像是真或假的标签
        real_labels = torch.ones(batch_size, 1).to(device)
        fake_labels = torch.zeros(batch_size, 1).to(device)

        # ================================================================== #
        #                      训练判别器                                    #
        # ================================================================== #

        # 定义判别器对真图片的损失函数
        outputs = D(images)
        d_loss_real = criterion(outputs, real_labels)
        real_score = outputs
        
        # 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        d_loss_fake = criterion(outputs, fake_labels)
        fake_score = outputs        
     
        # 得到判别器总的损失函数
        d_loss = d_loss_real + d_loss_fake
        
        # 对生成器、判别器的梯度清零        
        reset_grad()
        d_loss.backward()
        d_optimizer.step()
        
        # ================================================================== #
        #                        训练生成器                                  #
        # ================================================================== #

        # 定义生成器对假图片的损失函数，这里我们要求
        #判别器生成的图片越来越像真图片，故损失函数中
        #的标签改为真图片的标签，即希望生成的假图片，
        #越来越靠近真图片
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        
        
        g_loss = criterion(outputs, real_labels)
        
        # 对生成器、判别器的梯度清零
        #进行反向传播及运行生成器的优化器
        reset_grad()
        g_loss.backward()
        g_optimizer.step()
        
        if (i+1) % 200 == 0:
            print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}' 
                  .format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(), 
                          real_score.mean().item(), fake_score.mean().item()))
    
    # 保存真图片
    if (epoch+1) == 1:
        images = images.reshape(images.size(0), 1, 28, 28)
        save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))
    
    # 保存假图片
    fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
    save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))

# 保存模型
torch.save(G.state_dict(), 'G.ckpt')
torch.save(D.state_dict(), 'D.ckpt')

for epoch in range(num_epochs):

for i, (images, _) in enumerate(data_loader):

images = images.reshape(batch_size, -1).to(device)

# 定义图像是真或假的标签

real_labels = torch.ones(batch_size, 1).to(device)

fake_labels = torch.zeros(batch_size, 1).to(device)

# ================================================================== #

# 训练判别器 #

# ================================================================== #

# 定义判别器对真图片的损失函数

outputs = D(images)

d_loss_real = criterion(outputs, real_labels)

real_score = outputs

# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

d_loss_fake = criterion(outputs, fake_labels)

fake_score = outputs

# 得到判别器总的损失函数

d_loss = d_loss_real + d_loss_fake

# 对生成器、判别器的梯度清零

reset_grad()

d_loss.backward()

d_optimizer.step()

# ================================================================== #

# 训练生成器 #

# ================================================================== #

# 定义生成器对假图片的损失函数，这里我们要求

#判别器生成的图片越来越像真图片，故损失函数中

#的标签改为真图片的标签，即希望生成的假图片，

#越来越靠近真图片

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

g_loss = criterion(outputs, real_labels)

# 对生成器、判别器的梯度清零

#进行反向传播及运行生成器的优化器

reset_grad()

g_loss.backward()

g_optimizer.step()

if (i+1) % 200 == 0:

print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'

.format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(),

real_score.mean().item(), fake_score.mean().item()))

# 保存真图片

if (epoch+1) == 1:

images = images.reshape(images.size(0), 1, 28, 28)

save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))

# 保存假图片

fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)

save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))

# 保存模型

torch.save(G.state_dict(), 'G.ckpt')

torch.save(D.state_dict(), 'D.ckpt')

8.3.4 可视化结果

可视化每次由生成器得到假图片，即潜在向量z通过生成器得到的图片。

reconsPath = './gan_samples/fake_images-200.png'
Image = mpimg.imread(reconsPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

reconsPath = './gan_samples/fake_images-200.png'

Image = mpimg.imread(reconsPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

图8-7 GAN的新图片
图8-7明显好于图8-5。AVE生成图片主要依据原图片与新图片的交叉熵，而GAN真假图片的交叉熵，同时还兼顾了不断提升判别器和生成器本身的性能上。

8.4 VAE与GAN的异同

VAE适合于学习具有良好结构的潜在空间，潜在空间有比较好的连续性，其中存在一些有特定意义的方向。VAE能够捕捉到图像的结构变化（倾斜角度、圈的位置、形状变化、表情变化等）。这也是VAE的一个好处，它有显式的分布，能够容易地可视化图像的分布，具体如图8-8所示。

图8-8 AVE得到的数据流形分布图
GAN生成的潜在空间可能没有良好结构，但GAN生成的图像一般比VAE的更清晰。