1.序列建模概述
文章目录
卷积神经网络(CNN)善于处理网格化数据,如图像、视频等,虽然也可处理序列化数据,但应该不是它的强项,因序列化数据往往长短不一,而且序列数据往往与数据的前后位置有关,如我们经常看到的文本就是典型的序列数据。
如何对序列数据构建模型?早期通常采用统计语言模型(),统计语言模型的计算使用链式法则,把联合概率转换为条件概率,但随着序列长度的增长,其复杂度会指数级增长,为简化统计语言模型的计算,人们利用马尔科夫假设,这个假设的内容是:任何一个词出现的概率只和它前面的 1 个或若干个词有关。基于这个假设,人们提出n元语法(n -gram)模型。n -gram中的“n”很重要,它表示任何一个词出现的概率,只和它前面的 n-1 个词有关。
n元语法( n -gram),时间步t的词wt基于前面所有词的条件概率只考虑了最近时间步的n−1个词。如果要考虑比t−(n−1)更早时间步的词对wt的可能影响,我们需要增大n。但这样模型参数的数量将随之呈指数级增长,而一个词的语义往往跟比较长,为此,必须另辟蹊径。
n-gram 的优点有很多,首先它是一种直观的自然语言理解与处理方式,对参数空间进行了优化,并具有很强的解释性。它包含前 n-1 个词的全部信息,不会产生丢失和遗忘。除此以外,它还具有计算逻辑简单的优点 。
但与此同时,n-gram 也具有本质上的缺陷:n-gram 无法建立长期依赖,当 n 过大时仍会被数据的稀疏性严重影响,实际使用中往往仅使用 bigram 或 trigram;n-gram 基于频次进行统计,没有足够的泛化能力。因此,神经网络语言模型逐渐取代传统的统计自然语言模型成为主流,接下来我们对神经网络语言模型进行介绍。
首先实现这个转换的就是AI大咖Bengio ,在2003年发表在JMLR上发表了题为《A Neural Probabilistic Language Model》论文,在这篇具有开创性的论文中,有两个对NLP影响深远的创新点。一个是词向量,另一个是使用神经网络实现条件概率的计算。
不过Bengio提出的这个神经网络语言模型(NNLM),主要是实现和优化n-gram模型,除计算效率不高外,对序列基于固定长度,这点严重限制了NNLM的进一步发展。为解决长度可变及实现更长记忆,人们利用循环神经网络(RNN)来解决序列数据建模问题。利用循环神经网络无需刚性地记忆所有固定长度的序列,而是通过隐藏状态来存储(或记忆)之前时间步的信息,当然,由于RNN存在梯度消失问题,这种记忆一般是短时的,无法记忆较长的依赖关系,这点严重影响模型的性能。
解决长距离记忆问题,人们又提出一种RNN的几种改进模型,如LSTM模型、GRU模型等,这些模型中隐含状态的生成不像RNN一次性生成方法隐含状态,而是在原来内容的基础上添加一些新的内容。
虽然LSTM解决了序列模型的长距离依赖问题,但其计算只能严格从左到到右,或从右到左,无法实现并发处理。当前为了提升模型性能所要求的语料库也愈来愈大,这严重影响计算效率。
为了解决计算效率和长期依赖问题,最近人们又提出Transformer架构,使用这种架构既可解决长期依赖问题,又可很好的使用并发处理,从而极大提升模型性能及训练效率。在Transformer的基础上,人们提出了GPT、BERT、T5等预训练模型。这些模型在NLP领域打破了很多历史记录。
这里我们对序列建模的历史做了一个简单介绍,不涉及很多细节,接下来从业务场景、模型分解、可视化模型、模型拓展、模型实现等多个角度、多种方式、多个层次分别进行说明。
2统计语言模型
2.1统计语言模型
统计语言模型从统计的角度预测标记序列的概率分布,根据模型的设计,标记可以是词、字符等,这里我们以标记为词为例,对于句子ω_1,ω_2,⋯,ω_n的概率p(ω_1,ω_2⋯ω_n ),根据概率的链式法则,可求导整个句子的概率:
p(ω_1,ω_2⋯ω_n )=p(ω_1 )p(ω_2 |ω_1)p(ω_3 |ω_1,ω_2)⋯p(ω_n |ω_1,⋯ω_(n-1)) (1.1)
如何计算p(ω_n |ω_1,⋯ω_(n-1))?根据大数定律,该条件概率可利用极大似然估计来计算。
即,p(ω_n│ω_1,⋯ω_(n-1) )=(C(ω_1,⋯ω_(n-1),ω_n))/(C(ω_1,⋯ω_(n-1))) (1.2)
其中,C(.)表示子序列在语料库或数据集上的出现的次数。
这种计算方法存在两个致命的缺陷:一个缺陷是参数空间过大;另外一个缺陷是数据稀疏严重,长序列出现的频率非常低。
为了解决这个问题,通常引入了马尔科夫假设:一个词的出现仅仅依赖于它前面1个或有限的几个词,这就是接下来将介绍的n-gram模型。
2.2 n-gram模型
n-gram 是最为普遍的统计语言模型。它的基本思想是将文本里面的内容进行大小为 n 的滑动窗口操作,形成长度为 n 的短语子序列,利用最大似然估计,把条件概率的计算转换为对所有短语子序列的出现频度的计算。 直观上理解,n-gram 就是将句子长度缩短为只考虑前 n-1 个词。
如果一个词的出现不依赖于它前面的词,即句子中各词为相互独立,那么我们就称之为一元语法(或unigram),式(1.1)可表示为:
p(ω_1,ω_2⋯ω_n )=p(ω_1 )p(ω_2)p(ω_3)⋯p(ω_n)
如果一个词的出现仅依赖于它前面一个词,那么我们就称之为二元语法(或bigram)。式(1.1)可表示为:
p(ω_1,ω_2⋯ω_n )=p(ω_1 )p(ω_2 |ω_1)p(ω_3 |ω_2)⋯p(ω_n |ω_(n-1))
如果一个词的出现仅依赖于它前面出现的两个词,那么我们就称之为三元语法(或trigram)。式(1.1)可表示为:
p(ω_1,ω_2⋯ω_n )=p(ω_1 )p(ω_2 |ω_1)p(ω_3 |〖ω_1,ω〗_2)⋯p(ω_n |〖ω_(n-2),ω〗_(n-1))
在实践中用的最多的就是bigram和trigram了,而且效果很不错。高于四元的用的较少,因为训练它需要更庞大的语料,而且数据稀疏严重,时间复杂度高,精度却提高的不多。
这里举一个小数量的例子进行辅助说明:假设我们有一个语料库,如下:

<s>表示一个语句的开始,</s>表示一个语句的结束。
想要预测“我喜欢”这一句话的下一个字。我们分别通过 trigram 进行预测
通过 trigram,便是要对 P(w | 我喜欢)进行计算,经统计,“我喜欢她”出现了2次,“我喜欢车”出现了1次,通过最大似然估计可以求得P(她|我喜欢)=2/3,P(车|我喜欢)=1/3, 因此我们通过 bigram 预测出的整句话为: 我喜欢她
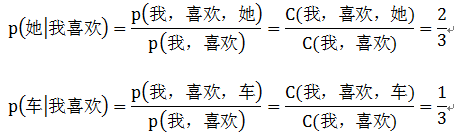
随着n的提升,我们拥有了更多的前置信息量,可以更加准确地预测下一个词。但这也带来了一个问题,数据随着n的提升变得更加稀疏了,导致很多预测概率结果为0。当遇到零概率问题时,我们可以通过平滑来缓解 n-gram 的稀疏问题。
2.3 n-gram的简单应用
搜索引擎(Baidu或者Google)、或者输入法的猜想或者提示。你在用百度时,输入一个或几个词,搜索框通常会以下拉菜单的形式给出几个像下图1-1一样的备选内容,这些备选内容其实是在猜想你想要搜索的那个词串。

图1-1 在百度输入关键字
图1-1中出现的词串(或短语)的排序,通过上面的介绍,你或许已发现,这其实是以n-gram模型为基础来实现的。
3 神经语言模型
3.2 循环神经网络语言模型
3.2.1 RNNCell架构
3.2.2 RNNCell代码实现
3.2.3 多层RNNCell
3.2.4 多层RNNCell代码实现
3.3 RNN生成文本实例
3.4 优化RNN
3.4.1 LSTMCELL
3.4.2 LSTMCell代码实现
3.4.3 多层LSTMCell结构
3.4.4 多层LSTMCell代码实现
3.4.5 LSTM架构
3.4.6 LSTM代码实现
3.4.7 biRNN
4 RNN应用实例(即将完成)
5 RNN拓展(即将完成)
5.1 ELMO
5.2 Encoder-Decoder
5.2 Attention and self-Attention
5.3 Transformer简介
5.4 BERT简介
5.5 GPT简介