第3章 矩阵基本运算
3.1矩阵加法
矩阵加法和乘法是矩阵运算中最常用的操作之一,两个矩阵相加,需要它们的形状相同,进行对应元素的相加,如:C=A+B,其中 。矩阵也可以和向量相加,只要它们的列数相同,相加的结果是矩阵每行与向量相加,这种隐式地复制向量b到很多位置的方式称为广播(broadcasting),以下我们通过一个代码实例来说明。
。矩阵也可以和向量相加,只要它们的列数相同,相加的结果是矩阵每行与向量相加,这种隐式地复制向量b到很多位置的方式称为广播(broadcasting),以下我们通过一个代码实例来说明。
|
1 2 3 4 |
C=np.array([[1,2,3],[4,5,6]]) b=np.array([10,20,30]) D=C+b print(D) |
打印结果为:
[[11 22 33]
[14 25 36]]
3.2矩阵点积
两个矩阵相加,要求它们的形状相同,
如果两个矩阵相乘,如A和B相乘,结果为矩阵C,矩阵A和B需要什么条件呢?条件比较简单,只要矩阵A的列数和矩阵B的行数相同即可。如果矩阵A的形状为m×n,矩阵B的形状为n×p,那么矩阵C的形状就是m×p,例如:
C=AB,则它们的具体乘法操作定义为:

即矩阵C的第i,j个元素 为矩阵的A第i行与矩阵B的第j列的点积。
为矩阵的A第i行与矩阵B的第j列的点积。
矩阵乘积有很多重要性质,如满足分配律A(B+C)=AB+AC 和结合律,A(BC)=(AB)C。大家思考一下是否满足交换律?
一般情况,交换律不成立,即
两个矩阵可以相乘,矩阵也可和向量相乘,只要矩阵的列数等于向量的行数或元素个数。如:

其中 。
。
3.3转置(transpose)
转置以主对角线(左上到右下)为轴进行镜像操作,通俗一点来说就是行列互换。将矩阵A转置表示为 ,定义如下:
,定义如下:

例3:
![A=\left[\begin{matrix}a_{1,1} & a_{1,2} &a_{1,3} \cr a_{2,1} & a_{2,2} &a_{2,3}\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f4dc5ea10897d8df5c4f8e90ea57ad29.gif)
![A^T=\left[\begin{matrix}a_{1,1} & a_{2,1} \\ a_{1,2} & a_{2,2}\cr a_{1,3} & a_{2,3} \end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_3b249ae388e4585cfb6918b8a84c312a.gif)
向量可以看作只有一列的矩阵,把向量x进行转置,得到下式。
![x^T=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b4758393f715cbecb421526c6f91676c.gif)
另外,相乘矩阵的转置也有很好性质,如: ,满足穿脱原则,如A、B像两件衣服,A先穿、B后穿,脱时反过来,
,满足穿脱原则,如A、B像两件衣服,A先穿、B后穿,脱时反过来, 在前,
在前, 在后。
在后。
用NumPy如何实现张量的转置?很简单,利用张量的T属性即可,示例如下:
|
1 2 3 4 |
C=np.array([[1,2,3],[4,5,6]]) D=C.T #利用张量的T属性(即转置属性) print(C) print(D) |
打印结果如下:
[[1 2 3]
[4 5 6]]
[[1 4]
[2 5]
[3 6]]
3.4矩阵的阿达马积
与向量的阿达马积相同,两个矩阵(如A、B)的阿达马积也是对应元素相乘,记为:
例4:
![\begin{aligned}A\odot B &=\left[\begin{matrix}1 & 2 & 3 \\ 4 & 5 &6\end{matrix}\right]\left[\begin{matrix}1 & 2 & 4 \\ 3 & 5 &0\end{matrix}\right]\\&=\left[\begin{matrix}1\times 1 & 2\times 2 & 3\times 4 \\ 4\times 3 &5\times 5 & 6\times 0\end{matrix}\right]\\&=\left[\begin{matrix}1 & 4 & 12 \\ 12 & 25 &0\end{matrix}\right]\end{aligned}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_88204ec1dabec5f057b2b9283b6bbaf2.gif)
两个矩阵对应元素的运算除相乘外,还有A+B、A-B、A/B等。
例5:用Python实现矩阵的阿达马积
|
1 2 3 4 5 |
A=np.array([[1,2,3],[4,5,6]]) B=np.array([[1,2,4],[3,5,0]]) #A、B的阿达马积 C=np.multiply(A,B) #或A*B print(C) |
运行结果如下:
[[ 1 4 12]
[12 25 0]]
例6:点积、对应元素运算在神经网络中的应用
神经网络的结构如下:
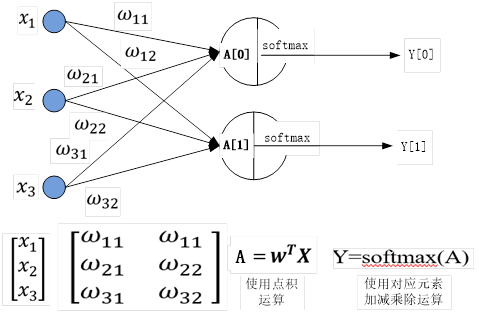
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
#定义激活函数softmax def softmax(A): C=np.max(A) exp_a=np.exp(A - C) #防溢出策略 sum_exp_a=np.sum(exp_a) y=exp_a/sum_exp_a return y #定义输入及权重参数 X=np.array([1,2,3]) W=np.array([[0.1,0.2],[0.2,0.3],[0.3,0.4]]) #实现输入与权重矩阵的点积 A=np.dot(W.T,X) #把A输入激活函数 Y=softmax(A) print(Y) |
运行结果
[0.35434369 0.64565631]
3.5行列式
一个 的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:
的方阵A的行列式记为det(A)或者|A|,一个2×2矩阵的行列式可表示如下:

把一个n阶行列式中的元素 所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素
所在的第i行和第j列划去后,留下来的n-1阶行列式叫做元素 的余子式,
的余子式,
记作 。记
。记 ,叫做元素
,叫做元素 的代数余子式。一个
的代数余子式。一个 矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即
矩阵的行列式等于其任意行(或列)的元素与对应的代数余子式乘积之和,即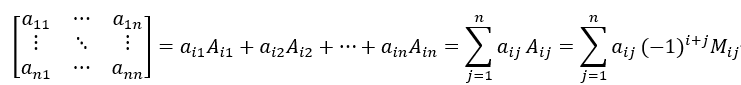
行列式的性质:
n阶矩阵的转置矩阵 的行列式等于A的行列式,即:
的行列式等于A的行列式,即:
方程组或矩阵或行列式的初等行变换:
(1)将行列式的两行交换;
(2)将行列式的某一行乘以k倍之后加到另一行。
第一种变换将使行列式的值反号,第2种变换行列式的值不变。
3.6迹运算
迹运算返回的是矩阵对角元素的和:

迹运算在某些场合非常有用。若不使用求和符号,有些矩阵运算很难描述,而通过矩阵乘法和迹运算符号可以清楚地表示。例如,迹运算提供了另一种描述矩阵Frobenius 范数的方式:

对迹运算的表达式,我们可以使用很多等式来表示。例如,迹运算在转置运算下是不变的:

多个矩阵相乘得到的方阵的迹,和将这些矩阵中的最后一个挪到最前面之后相乘的迹是相同的。当然,我们需要考虑挪动之后矩阵乘积依然有定义:
Tr(ABC)=Tr(CAB)=Tr(BCA)
利用Python的NumPy对矩阵求迹同样方便。请看以下示例。
|
1 2 3 4 5 6 7 8 9 10 11 |
C=np.array([[1,2,3],[4,5,6],[7,8,9]]) TrC=np.trace(C) D=C-2 TrCT=np.trace(C.T) TrCD=np.trace(np.dot(C,D)) TrDC=np.trace(np.dot(D,C)) print(TrC) print(TrCT) print(TrCD) print(TrDC) |
打印结果:
15
15
171
171