第6章 矩阵分解

6.1特征值分解概述

一个矩阵的特征值非常重要，如何获取这些特征？通过解特征方程是一种方法，但效率比较低，如果矩阵A的维度较大，使用这种方法就如此，是否有更好的方法呢？接下来我们介绍几种通过矩阵分解来获取特征值的方法。

6.1.1 特征值分解

特征值分解（Eigen Value Decomposition，简称EVD），又称谱分解（Spectral decomposition）是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。需要注意只有对可对角化矩阵才可以施以特征分解。本节讨论的矩阵除非特别说明一般指方阵。
假设矩阵A有n个线性无关的特征向量[v^1,v^2,\cdots,v^n],它们对应的特征值为[\lambda_1,\lambda_2,\cdots,\lambda_n]，并按从大到小进行排序。
把这n个线性无关的特征向量组合成一个新方阵，每一列是一个特征向量。
V=[v^1,v^2,\cdots,v^n]
用特征值构成一个n阶对角矩阵，对角线的元素都是特征值。
\begin{equation}\wedge=\begin{bmatrix}\lambda_{1} & & & \\ & \lambda_{2} & & \\ & & \ddots &\\ & & &\lambda_{n}\end{bmatrix}\end{equation}
那么，A的特征分解可表示为：
A=V\wedge V^{-1}\tag{6.1}
注意，并不是所有方阵都能进行特征值分解，一个n阶方阵A能进行特征值分解的充分必要条件是它含有n个线性无关的特征向量。
特征值的大小与权重密切相关，特征值大的说明在矩阵A的权重就大。利用这个特性可以对矩阵A进行压缩或简化。

6.1.2 对称矩阵的分解

如果n阶矩阵A为实对称矩阵，可以对A进行特征值分解为：
A=Q\wedge Q^T\tag{6.2}
其中Q为正交矩阵，它的列由A的正交处理后的特征向量，Λ是A的特征值构成的对角矩阵。
例1 ：判断矩阵A=\left(\begin{matrix}-1&1&0 \\ -4&3&0 \\ 1&0&2\end{matrix}\right)是否可以进行特征值分解？
解：具体 步骤如下：
（1）创建A的特征方程，并求出特征值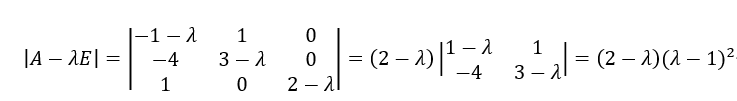
解得:\lambda_1=2,\lambda_2=\lambda_3=1
（2）把特征值代入方程组：\left(A-\lambda E\right)x=0，求出对应的特征向量。
当\lambda=2时，解方程(A-2E)x=0，得x_1=0,x_2=0,x_3=1,对应特征向量v1=\left(\begin{matrix}0 \\ 0 \\ 1\end{matrix}\right)
当\lambda=1时，方程(A-E)x=0的秩为2.只有一个特征向量，如v2=\left(\begin{matrix}-1 \\ -2 \\ 1\end{matrix}\right)，故矩阵A没有3个线性无关的特征向量。所以A不能进行特征值分解。