文章目录
第6章 机器学习基础
在本书的第一部分,我们介绍了NumPy、TensorFlow基础等内容,这些内容是继续学习TensorFlow的基础。在第二部分,我们将介绍深度学习的一些基本内容,以及如何用TensorFlow解决机器学习、深度学习的一些实际问题。
深度学习是机器学习的重要分支,也是机器学习的核心,它是在机器学习的基础上发展起来的,因此在了解深度学习之前,理解机器学习的基本概念、基本原理会对对理解深度学习大有裨益。
机器学习的体系很庞大,限于篇幅,本章主要介绍基本知识及其与深度学习关系比较密切的内容,如果读者希望进一步学习机器学习的相关知识,建议参考周志华老师的《机器学习》或李航老师的《统计学习方法》。
本章先介绍机器学习中常用的监督学习、无监督学习等,然后介绍神经网络及相关算法,最后介绍传统机器学习中的一些不足及优化方法等,主要内容如下:
♦机器学习的一般流程
♦监督学习
♦无监督学习
♦机器学习实例
6.1 机器学习的一般流程
机器学习一般流程包括明确目标、收集数据、探索数据、预处理数据,对数据处理后,接下来开始构建和训练模型、评估模型,然后优化模型等步骤,图6-1为机器学习一般流程图。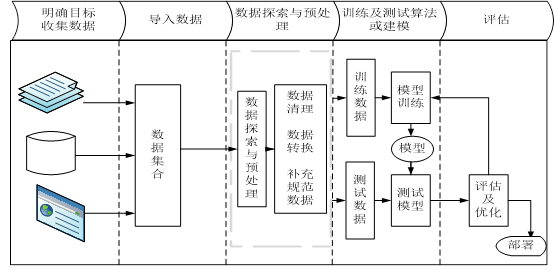
图6-1 机器学习一般流程图
通过这个图形可直观了解机器学习的一般步骤或整体架构,接下来我们就各部分分别加以说明。
6.1.1 明确目标
在实施一个机器学习项目之初,定义需求、明确目标、了解要解决的问题以及目标涉及的范围等非常重要,它们直接影响后续工作的质量甚至成败。明确目标,首先需要明确大方向,比如当前需求是分类问题还是预测问题或聚类问题等。清楚大方向后,需要进一步明确目标的具体含义。如果是分类问题,还需要区分是二分类、多分类或多标签分类;如果是预测问题,要区别是标量预测还是向量预测;其他方法类似。确定问题,明确目标有助于选择模型架构、损失函数及评估方法等。
当然,明确目标还包含需要了解目标的可行性,因为并不是所有问题都可以通过机器学习来解决。
6.1.2 收集数据
目标明确后,接下来就是了解数据。为解决这个问题,需要哪些数据?数据是否充分?哪些数据能获取?哪些无法获取?这些数据是否包含我们学习的一些规则等等,都需要全面把握。
接下来就是收集数据,数据可能涉及不同平台、不同系统、不同部分、不同形式等,对这些问题的了解有助于确定具体数据收集方案、实施步骤等。
能收集的数据尽量实现自动化、程序化。
6.1.3 数据探索与预处理
收集到的数据,不一定规范和完整,这就需要对数据进行初步分析或探索,然后根据探索结果与问题目标,确定数据预处理方案。
对数据探索包括了解数据的大致结构、数据量、各特征的统计信息、整个数据质量情况、数据的分布情况等。为了更好体现数据分布情况,数据可视化是一个不错方法。
通过对数据探索后,可能发会现不少问题:如存在缺失数据、数据不规范、数据分布不均衡、存在奇异数据、有很多非数值数据、存在很多无关或不重要的数据等等。这些问题的存在直接影响数据质量,为此,数据预处理工作应该就是接下来的重点工作,数据预处理是机器学习过程中必不可少的重要步骤,特别是在生产环境中的机器学习,数据往往是原始、未加工和处理过,数据预处理常常占据整个机器学习过程的大部分时间。
数据预处理过程中,一般包括数据清理、数据转换、规范数据、特征选择等工作。
6.1.4 模型选择
数据准备好以后,接下就是根据目标选择模型。模型选择上可以先用一个简单、自己比较熟悉的一些方法来实现一个原型或比基准更好一点的模型。通过这个简单模型有助于你快速了解整个项目的主要内容。
•了解整个项目的可行性、关键点。
•了解数据质量、数据是否充分等。
•为你开发一个更好模型奠定基础。
在进行模型选择时,一般不存在某种对任何情况都表现很好的算法(这种现象又称为没有免费的午餐)。因此在实际选择时,一般会选用几种不同方法来训练模型,然后比较它们的性能,从中选择最优的那个。
模型选择好后,还需要考虑以下几个关键点:
•最后一层是否需要添加softmax或sigmoid激活层;
•选择合适损失函数。
表6-1 列出了常见问题类型最后一层激活函数和损失函数的对应关系,供大家参考。
表6-1 根据问题类型选择损失函数
| 问题类型 | 最后一层激活函数 | 损失函数 |
| 回归模型 | tf.losses.(或tf.keras.losses.)
mean_squared_error(函数形式,简写为 mse) MeanSquaredError(类形式,简写为MSE) |
|
| SVM | hinge | |
| 二分类模型 | binary_crossentropy(函数形式)
BinaryCrossentropy(类形式) |
|
| 多分类模型 | label是类别序号编码 | categorical_crossentropy |
| label进行了独热编码 | sparse_categorical_crossentropy | |
| 自定义损失函数 | 自定义损失函数接收两个张量y_true,y_pred作为输入参数,并输出一个标量作为损失函数值; 也继承tf.keras.losses.Loss类,重写call方法实现损失的计算逻辑,从而得到损失函数的类的实现。 | |
。
6.1.5 模型评估
模型确定后,还需要确定一种评估模型性能的方法,即评估方法。评估方法大致有以下三种:
•留出法(holdout):留出法的步骤相对简单,直接将数据集划分为两个互斥的集合,其中一个集合作为训练集,另一个作为测试。在训练集上训练出模型后,用测试集来评估测试误差,作为泛化误差的估计。使用留出法,还有一种更好的方法就是把数据分成三部分:训练数据集、验证数据集、测试数据集。训练数据集用来训练模型,验证数据集用来调优超参数,测试集用来测试模型的泛化能力。数据量较大时可采用这种方法,整个过程可用图6-2表示。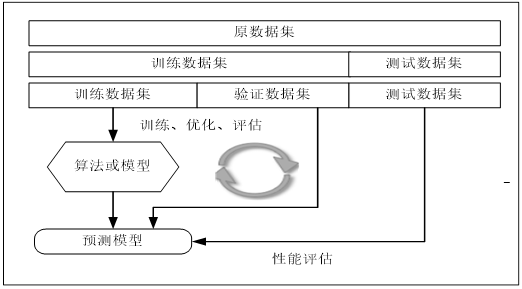
图6-2 留出法实施步骤
•K折交叉验证:不重复地随机将训练数据集划分为k个,其中k-1个用于模型训练,剩余的一个用于测试,具体如图6-3所示。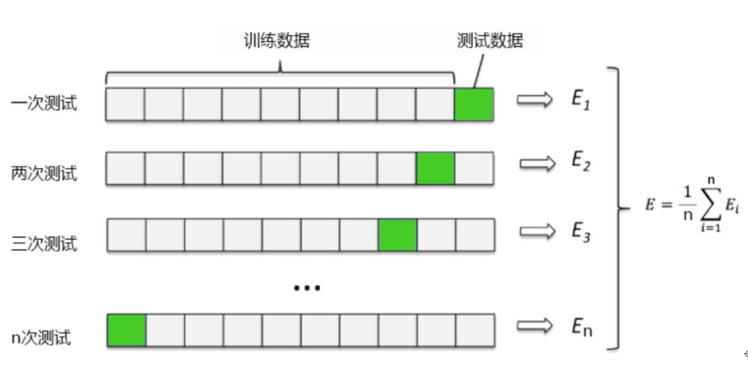
图6-3 K折交叉验证法的实施步骤
•重复的K折交叉验证:当数据量比较小,数据分布不很均匀时可以采用这种方法。
使用训练数据构建模型后,通常使用测试数据对模型进行测试,测试模型对新数据的
测试。如果对模型的测试结果满意,就可以用此模型对以后的进行预测;如果测试结果不满意,可以优化模型。优化的方法很多,其中网格搜索参数是一种有效方法,当然我们也可以采用手工调节参数等方法。如果出现过拟合,尤其是回归类问题,可以考虑正则化方法来降低模型的泛化误差。
6.1.6 评估指标
评估指标及其概述如表6-2所示。
表6-2 评估指标概述
| 问题类型 | 最后一层激活函数 | 评估指标 |
| 回归模型 | tf.losses.(或tf.keras.losses.)
mean_squared_error(函数形式,简写为 mse) MeanSquaredError(类形式,简写为MSE) |
|
| 二分类模型 |
要求y_true(label)为onehot编码形式 要求y_true(label)为序号编码形式 |
Accuracy (准确率)
Precision (精确率) Recall (召回率) CategoricalAccuracy(分类准确率,与Accuracy含义相同 SparseCategoricalAccuracy (稀疏分类准确率,与Accuracy含义相同 |
| 多分类模型 | 要求y_true(label)为onehot编码形式 | TopKCategoricalAccuracy (多分类TopK准确率) |
| 要求y_true(label)为序号编码形式 | SparseTopKCategoricalAccuracy (稀疏多分类TopK准确率) |
6.2 监督学习
机器学习大致可分为监督学习(Supervised learning)、无监督学习(Unsupervised learning)和半监督学习(Semi-supervised learning)。这节主要介绍监督学习有关算法。
监督学习的数据集一般含有很多特征或属性,数据集中的样本都有对应标签或目标值。监督学习的任务就是根据这些标签,学习调整分类器的参数,使其达到所要求性能的过程。简单来说,就是由已知推出未知。监督学习过程如图6-4所示。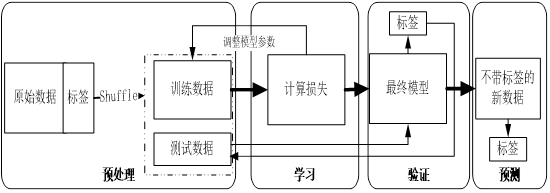
图6-4 监督学习过程
6.2.1 线性回归
线性回归是线性模型中的一种,在介绍线性回归之前,我们先简单介绍一下线性模型。线性模型是监督学习中比较简单的一种模型虽然简单,但却非常有代表性,而且是线性模型其他算法的很好入口。
线性模型的任务是:在给定样本数据集上(假设该数据集特征数为n),学习得到一个模型或一个函数f(z),使得对任意输入特征向量 ,f(z)能表示为X的线性函数,即满足:
,f(z)能表示为X的线性函数,即满足:
设  ,则有:
,则有:

其中 ,b为模型参数,这些参数需要在训练过程学习或确定。
,b为模型参数,这些参数需要在训练过程学习或确定。
把式(6.1)写成矩阵的形式:

其中 
线性模型可以用于分类、回归等学习任务,具体包括线性回归、逻辑回归等算法,另外我们从式(6.2)可以看出,它与单层神经网络(又称为感知机,如图6-5)的表达式一致,因此,人们往往也把单层神经网络纳入线性模型范围中。单层神经网络属于神经网络,具体将在本书第7章介绍。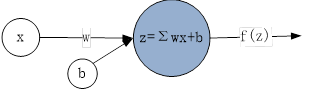
图6-5单层单个神经元
回归一般用于预测,当然也可用于分类,下节的逻辑回归就是用于分类任务。线性回归是回归学习中的一种,其任务就是在给定的数据集D中,通过学习得到一个线性模型或线性函数f(x),使得数据集与函数f(x)之间具有式(6.1)的关系,如果把这种函数关系可视化就是图6-6。
图6-6 线性回归示意图
图6-6中这条直线是如何训练出来的呢?要画出这条直线(f(x)=wx+b),就需要知道直线的两个参数:w和b。如何求w和b?那就需要用到所有的已知条件:样本(含x和目标值或标签),样本用字符可表示为:
这里假设共有m个样本,每个样本由输入特征向量 和目标值
和目标值 构成,其中
构成,其中 一般是向量,如
一般是向量,如 是目标值(又称为实际值或标签),
是目标值(又称为实际值或标签),
它是一个实数,即 。为简单起见,我们假设x^i是一维的,所以样本就是图6-6中的各个点。
。为简单起见,我们假设x^i是一维的,所以样本就是图6-6中的各个点。
根据这些点,如何拟合预测函数或直线:f(x)=wx+b 呢?通过这些点,可以画出很多类似的直线,在这些直线中哪条直线最能反应这些样本的特点呢?
这里就涉及一个衡量标准问题,通常用一个代价函数来表示:

式(6.3)直观的解释就是,这m个样本点的预测值 与实际值
与实际值 的距离最小。满足这个条件的直线应该就是最好的。
的距离最小。满足这个条件的直线应该就是最好的。
而 ,把它代入式(6.3)就是:
,把它代入式(6.3)就是:

所以上述拟合直线问题,就转换为求代价函数L(w,b)的最小值问题。求解式(6.4)的最小值问题,我们可以使用:
1)利用迭代法,每次迭代沿梯度的反方向(如图6-7),逐步靠近或收敛最小值点;
2)利用最小二乘法,直接求出参数w,b。
我们通常采用第一种方法,具体实现请参考6.5节,第二种方法计算量比较大而且复杂。这里就不再展开。
图6-7梯度下降法
6.2.2 逻辑回归
上节我们介绍了线性回归,利用线性回归来拟合一条直线,这条直线就是一个函数或一个模型,根据这个函数我们就可以对新输入数据x进行预测,即根据输入x,预测其输出值y。这是一个典型的回归问题。线性模型除了用于回归,也可用于分类。最常用的方法就是逻辑回归(Logistic Regression)。分类顾名思义就是根据数据集的特点划分成几类,其输出为有限的离散值,如{A,B,C}、{是,否}、{0,1}等。图6-8为逻辑回归分类可视化示意图。
图6-8逻辑回归分类
其任务就是在数据集D={若干圆点、若干小方块}中,找出一条直线或曲线,把这两类点区分开。划分结果,在直线一边尽可能为同一类的点,如圆点,在直线另一边尽可能是另一类的点,如小方块,如图6-8所示。目标明确以后,如何求出拟合分类直线或这条直线的表达式呢?当然这条直线的表达式不像式(6.1),其输出结果最好为是或否,或为0或1,其表达式为:

其中 称为划分边界。
称为划分边界。
式(6.5)虽然结果很完备,如果能这样当然最好,不过因这个函数不连续,所以我们一般转向次优的方案,采用sigmoid函数:

其对应的函数曲线如图6-9所示。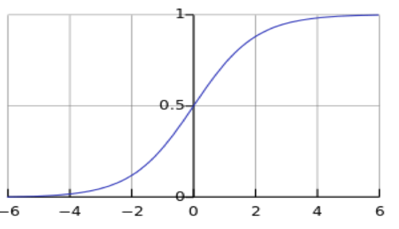
图6-9 sigmoid函数曲线
该函数将输出数据压缩为0到1之间的范围内,这也是概率取值范围,如此便可将分类问题转换为一个概率问题来处理。把 代入式(6.6)便可得到逻辑回归的预测函数:
代入式(6.6)便可得到逻辑回归的预测函数:

对于二分类问题,我们可以用预测y=1或0的概率表示为:


模型的函数表达式确定后,剩下就是如何去求解模型中的参数(如w、b)。与线性回归一样,要确定参数,需要使用代价函数。逻辑回归属于分类问题,此时就不宜用式(6.3)的代价函数。
如果还用式(6.3)为代价函数,这样我们会发现L(w,b)为非凸函数,此时就存在很多局部极值点,就无法用梯度迭代得到最终的参数,因此分类问题通常采用对数最大似然作为代价函数:

这节我们介绍了线性模型中线性回归和逻辑回归及其简单应用。分类中使用的数据集比较理想的线性数据集。但实际上生活中很多数据集是非线性数据集,对非线性数据集我们该如何划分呢?下节我们将介绍一种强大的分类器——支持向量机(SVM),它不但可以处理线性数据集,也可以处理非线性数据集。
6.2.3 树回归
前面我们介绍了线性回归、逻辑回归等,这节将介绍树回归。在介绍树回归之前,先简单介绍一下决策树。决策树一般用来做分类,但也有一些决策树可用来做回归预测,如CART决策树,有些场景用决策树做回归效果还更好。如图6-10,把决策树转换为回归模型示意图。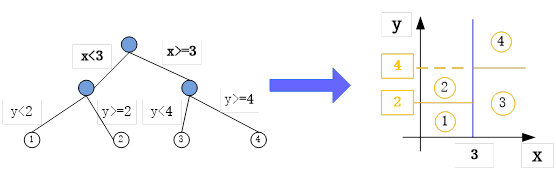
图6-10 把树形结构转换为回归模型示意图
图6-11对比了使用线性回归与树回归的可视化效果,在该场景,树回归的性能高于线性回归的性能。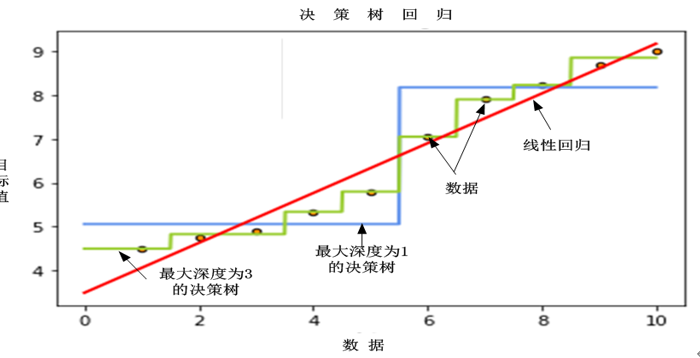
图6-11线性回归与树回归的可视化效果比较
6.2.4 支持向量机
支持向量机(Support Vector Machine,SVM),在处理线性数据集、非线性数据集时都有较好效果。在机器学习或者模式识别领域可谓无人不知,无人不晓。在20世纪八九十年代,支持向量机曾和神经网络一决雌雄,独领风骚几十年,甚至有人把神经网络八九十年代的再度沉寂归功于它。
它的强大或神奇与它采用的相关技术不无关系,如最大类间隔、松弛变量、核函数等等,使用这些技术使其在众多机器学习方法中脱颖而出。即使几十年过去了,仍风采依旧,究其原因,与其高效、简洁、易用的特点分不开。其中一些处理思想与当今深度学习技术有很大关系,如使用核方法解决非线性数据集分类问题的思路,类似于带隐含层的神经网络,可以说两者有同工异曲之妙。
用支持向量机进行分类,目的与逻辑回归类似得到一个分类器或分类模型,不过它的分类器是一个超平面(如果数据集是二维,这个超平面就是直线,三维数据集,就是平面,以此类推),这个超平面把样本一分为二,当然,这种划分不是简单划分,需要使正例和反例之间的间隔最大。间隔最大,其泛化能力就最强。如何得到这样一个超平面?下面我们通过一个二维空间例子来说明。
1.最优间隔分类器
SVM的分类器为超平面,何为超平面?哪种超平面是我们所需要的?我们先看图6-12的几个超平面或直线。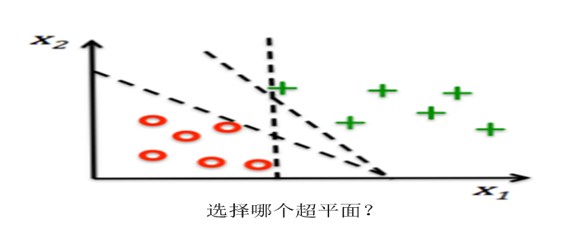
图6-12 SVM 超平面
如何获取最大化分类间隔?分类算法的优化目标通常是最小化分类误差,但对SVM而言,优化的目标是最大化分类间隔。所谓间隔是指两个分离的超平面间的距离,其中在超平面H1和H2上的训练样本又称为支持向量(support vector)。
假设一个二维空间的数据集分布如图6-13所示(图中的样本点有些是圆点,有些是方块)。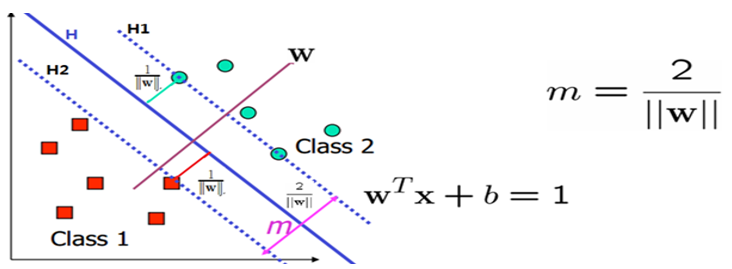
图6-13 支持向量机样本点
其中,
![W=[w1,w2],X=[x1,x2] or [x,y]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b88572d7864ded7e56c46782e8dc4822.gif)
接下来我们需要用这些样本去训练学习一个线性分类器(超平面),这里就是直线H: ,
,
也就是 大于0时,输出+1,小于0时,输出-1,其中sgn()表示取符号。而
大于0时,输出+1,小于0时,输出-1,其中sgn()表示取符号。而 就是我们要寻找的分类超平面(即直线H),
就是我们要寻找的分类超平面(即直线H),
如上图6-8所示。我们需要这个超平面尽可能分隔这两类,即这个分类面到这两个类的最近的那些样本的距离相同,
而且最大。为了更好的说明这个问题,假设我们在上图6-8中找到了两个和这个超平面并行且距离相等的超平面: 和
和  。
。
这时候我们就需要两个条件:
1)没有任何样本在这两个平面之间;
2)这两个平面的距离需要最大。
有了超平面以后,我们就可以对数据集进行划分。不过还有一个关键问题,如何把非线性数据集转换为线性数据集?这就是下节要介绍的内容,利用核函数技术,把非线性数据集映射到一个更高或无穷维的空间,在新空间转换为线性数据集。
2.核函数
核函数如何把线性不可分数据集转换为线性可分数据集呢?为了给大家一个直观的认识,我们先来看图6-14,直观感受一下SVM的核威力。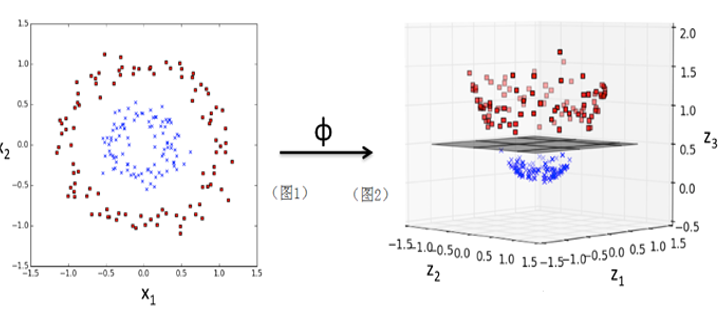
图6-14 SVM 核函数数据集映射
图6-14左边为一个线性不可分数据集,中间为一个核函数 :
:

其功能就是将左边在二维空间线性不可分的数据集,映射到三维空间后变成了一个线性可分数据集,其中超平面可以把数据分成上下两部分。这里使用的核为一个多项式核: 。除了用多项式核,还可以用其他核,如:
。除了用多项式核,还可以用其他核,如:
•径向基核函数(Radial Basis Function),又称为高斯核:

•sigmoid核

SVM添加核函数,就相当于在神经网络中添加了隐含层,所以SVM曾经风靡一时。但目前已被神经网络,尤其是深度学习所超越,原因很多,SVM核函数比较难选择是重要原因。此外,灵活性、扩展性也不如神经网络。神经网络将在第7章介绍。
6.2.5 朴素贝叶斯分类器
概率论是许多机器学习算法的基础,所以熟悉这一主题非常重要。朴素贝叶斯是一种基于概率论来构建分类器的经典方法。
一些概率模型,在监督学习的样本集中能获得非常好的分类效果。在许多实际应用中,朴素贝叶斯模型参数估计使用最大似然估计方法。
1.极大似然估计
概率模型的训练过程就是一个参数估计过程,对于参数估计,在统计学界有两个派别,即频率派和贝叶斯派,提出了不同的思想和解决方案,这些方法各有自己的特点和理论依据。频率派认为参数虽然未知,但却是固定的,因此,可以通过优化似然函数等准则来确定;贝叶斯派认为参数是随机值,因为没有观察到,与一个随机数也没有什么区别,因此参数可以有分布,也就是说,可以假设参数服从一个先验分布,然后基于观察到的数据计算参数的后验分布。
本节介绍的极大似然估计(Maximum Likelihood Estimate,MLE)属于频率派。如何求解极大似然估计呢?以下为求解MLE的一般过程:
1) 写出似然函数。
假设我们有一组含m个样本数据集 ,由分布P(x;θ)独立生成,则参数θ对于数据集X的似然函数为:
,由分布P(x;θ)独立生成,则参数θ对于数据集X的似然函数为:

概率乘积不方便计算,而且连乘容易导致数值下溢,为了得到一个便于计算的等价问题,通常使用对数似然。
2) 对似然函数取对数,整理得:

3) 利用梯度下降法,求解参数θ。根据式(6.15),极大似然估计可表示为: 
2.朴素贝叶斯分类器
前面我们介绍了利用逻辑回归(LR)、支持向量机(SVM)进行分类,这里我们介绍一种新的分类方法。这种方法基于贝叶斯定理,同时假设样本的各特征之间是独立且互不影响,这就是朴素贝叶斯分类器,假设特征互相独立是称其为“朴素”的重要原因。
利用LR或SVM进行分类的一般步骤为:
1)定义模型函数:y=f(x)或p(y|x)。
2)定义代价函数。
3)利用梯度下降方法,求出模型函数中的参数。
如果我们用朴素贝叶斯分类器进行分类,其步骤是否与LR或SVM的一样呢?要回答这个问题,我们首先看一下朴素贝叶斯分类器的主要思想。
假设给定输入数据x及类别c,在给定输入数据x的条件下,求属于类别c的概率p(c|x),那么朴素贝叶斯公式可表示为:

朴素贝叶斯分类的基本思想就是,通过求取p(c)和p(x|c)来求p(c|x),而不是直接求p(c|x),利用式(6.17)求最优分类,p(x)对所有类别都是相同的。
输入数据x一般含有多个特征或多个属性,假设有n个特征,即 ,那么计算p(x|c)比较麻烦,需要计算在条件c下的联合分布。好在朴素贝叶斯有“属性条件独立性”这个假设,计算p(x|c)时就方便多了。p(x|c)就可以写成:
,那么计算p(x|c)比较麻烦,需要计算在条件c下的联合分布。好在朴素贝叶斯有“属性条件独立性”这个假设,计算p(x|c)时就方便多了。p(x|c)就可以写成:

假设类别集合为Y,p(x)对所有类别都相同,因此输入数据x条件下,最优分类就可表示为:

由此,我们可以看出,利用贝叶斯分类器进行分类,不是首先定义P(c|x),而是先求出P(x|c),然后求出不同分类下的最优值,期间不涉及求代价函数。
6.2.6 集成学习
集成学习(Aggregation)为什么能起到1+1>2的效果?集成学习的原理与盲人摸象这个故事揭示的道理类似,即综合多个盲人的观点就能得到一个更全面的观点。
我们知道艺术来源于生活,又高于生活,实际上很多算法也是如此。在介绍集成学习之前,我们先看一下生活中的集成学习。假如你有m个朋友,每个朋友向你推荐明天某支股票是涨还是跌,对应的建议分别是t_1,t_2,⋯,t_m。那么你该选择哪个朋友的建议呢?你可能会采用如下几种方法。
•第一种方法,是从m个朋友中选择一个最受信任,对股票预测能力最强的,直接听从其建议就好。这是一种普遍的做法。
•第二种方法,如果每个朋友在股票预测方面都是比较厉害的,都有各自的专长,那么就同时考虑m个朋友的建议,将所有结果做个投票,一人一票,最终决定出对该支股票的预测。
•第三种方法,如果每个朋友水平不一,有的比较厉害,投票比重应该更大一些;有的比较差,投票比重应该更小一些。那么,仍然对m个朋友进行投票,只是每个人的投票权重不同。
•第四种方法与第三种方法类似,但是权重不是固定的,根据不同的条件,给予不同的权重。比如,如果是传统行业的股票,那么给这方面比较厉害的朋友较高的投票权重,如果是服务行业,那么就给这方面比较厉害的朋友较高的投票权重。
上述四种方法都是将不同人不同意见融合起来的方式,接下来我们来讨论如何将这些做法对应到机器学习中去。集成学习的思想与这个例子类似,即把多个人的想法结合起来,以得到一个更好、更全面的想法。
集成学习的主要思想:对于一个比较复杂的任务,综合许多人的意见来进行决策往往比一家独大好,正所谓集思广益。其过程如图6-15所示。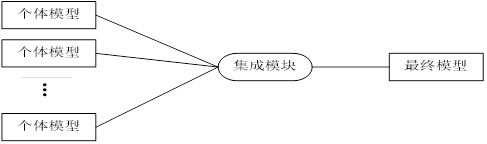
图6-15集成学习示例
接下来介绍两种典型的集成学习:装袋(Bagging)算法和提升分类器(Boosting)。
1. Bagging
Bagging即套袋法,其算法过程如下。
1) 从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本。Bootstrapping算法是指利用有限的样本经由多次重复抽样,重新建立起足以代表母体样本分布之新样本。在训练集中,有些样本可能被多次抽取到,而有些样本可能一次都没有被抽中。共进行k轮抽取,得到k个训练集。这k个训练集之间是相互独立的。
2)每次使用一个训练集得到一个模型,k个训练集共得到k个模型。训练时我们可以根据具体问题采用不同的分类或回归方法,如决策树、单层神经网络等。
3)针对分类问题:将上步得到的k个模型采用投票的方式得到分类结果;针对回归问题,计算上述模型的均值并将其作为最后的结果。
随机森林是Bagging算法的典型代表,在随机森林中,每个树模型都是装袋采样训练的。另外,特征也是随机选择的,最后对于训练好的树也是随机选择的。
这种处理的结果是随机森林的偏差增加的很少,而由于对弱相关树模型的结果进行平均,方差也得以降低,最终得到一个方差小,偏差也小的模型。
2. Boosting
Boosting是指通过算法集合将弱学习器转换为强学习器。Boosting的主要原则是训练一系列的弱学习器,所谓弱学习器是指仅比随机猜测好一点点的模型,例如较小的决策树,训练的方式是利用加权的数据。在训练的早期对于错分数据给予较大的权重。
对于训练好的弱分类器,如果是分类任务按照权重进行投票,而对于回归任务进行加权,然后再进行预测。boosting和bagging的区别在于是对加权后的数据利用弱分类器依次进行训练。
Boosting是一族可将弱学习器提升为强学习器的算法,这族算法的工作机制类似,分析如下:
•先从初始训练集训练出一个基学习器;
•再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注;
•基于调整后的样本分布来训练下一个基学习器;
•重复进行上述步骤,直至基学习器数目达到事先指定的值T,最终将这T个基学习器进行加权结合。
下面我们通过一些图形来说明。
1)假设我们有如下样本,如图6-16所示。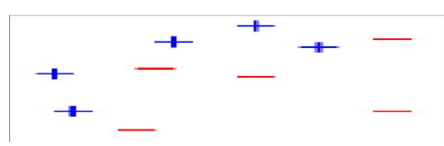
图6-16 最初样本图
2)对以上数据集进行替代式分类。第1次分类,得到以下划分,如图16-17所示。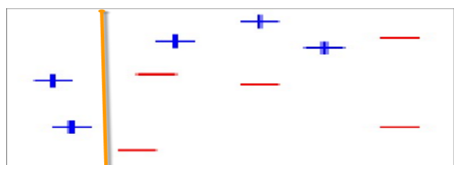
图6-17 第1次划分后的样本图
第2次分类,得到以下划分,如图6-18所示。
图6-18 第2次划分后的样本图
在图6-18中被正确测的点有较小的权重(尺寸较小),而被预测错误的点(+)则有较大的权重(尺寸较大)。
第3次分类,得到以下划分,如同6-19所示。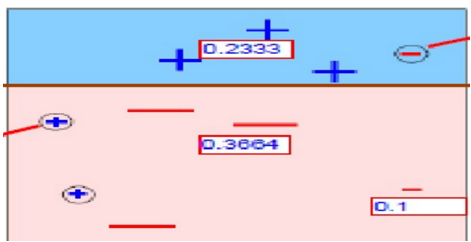
图6-19 第3次划分后的样本图
在图6-19中被正确测的点有较小的权重(尺寸较小),而被预测错误的点(-)则有较大的权重(尺寸较大)。
第4次综合以上分类,得到最后的分类结果。如图6-20所示。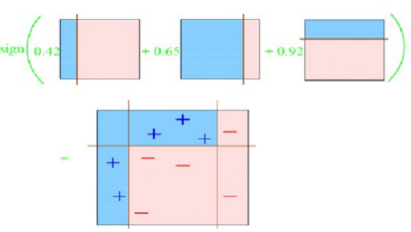
图6-20 最后的分类结果
基于Boosting思想的算法主要有AdaBoost、GBDT、XGBoost等。
6.3 无监督学习
上节我们介绍了监督学习,监督学习的输入数据中有标签或目标值,但在实际生活中,有很多数据是没有标签的,或者标签代价很高,对这些没有标签的数据该如何学习呢?这类问题可用机器学习中的无监督学习。在无监督学习中,我们通过推断输入数据中的结构来建模。如通过提取一般规律,或通过数学处理系统地减少冗余,或者根据相似性组织数据等,这分别对应无监督学习的关联学习、降维、聚类。无监督学习方法很多,限于篇幅我们这里只介绍两种典型的无监督算法:主成分分析与k均值(k-means)算法。
6.3.1主成分分析
主成分分析(Principal Components Analysis,PCA)是一种数据降维技术,可用于数据预处理。如果我们获取的原始数据维度很大,比如1000个特征,在这1000个特征中可能包含了很多无用的信息或者噪声,真正有用的特征可能只有50个或更少,那么我们可以运用PCA算法将1000个特征降到50个特征。这样不仅可以去除无用的噪声,节省计算资源,还能保持模型性能变化不大。如何实现PCA算法呢?
为便于理解,我们从直观上来理解就是,将数据从原多维特征空间转换到新的维数更低的特征空间中。例如原始的空间是三维的(x,y,z),x、y、z分别是原始空间的三个基,我们可以通过某种方法,用新的坐标系(a,b,c)来表示原始的数据,那么a、b、c就是新的基,它们组成新的特征空间。在新的特征空间中,可能所有的数据在c上的投影都接近于0,即可以忽略,那么我们就可以直接用(a,b)来表示数据,这样数据就从三维的(x,y,z)降到了二维的(a,b)。如何求新的基(a,b,c)?以下介绍求新基的一般步骤:
1)对原始数据集做标准化处理;
2)求协方差矩阵;
3)计算协方差矩阵的特征值和特征向量;
4)选择前k个最大的特征向量,k小于原数据集维度;
5)通过前k个特征向量组成了新的特征空间,设为W;
6)通过矩阵W,把原数据转换到新的k维特征子空间。
6.3.2 k均值算法
前面我们介绍了分类,那聚类与分类有何区别呢?分类是根据一些给定的已知类别标识的样本,训练模型,使它能够对未知类别的样本进行分类。这属于监督学习。而聚类指事先并不知道任何样本的类别标识,希望通过某种算法来把一组未知类别的样本划分成若干类别,它属于无监督学习。K均值算法就是典型的聚类算法。那么k均值算法如何实现聚类呢?它的基本思想是:
1)适当选择k个类的初始中心;
2)在第i次迭代中,对任意一个样本,求其到K个中心的距离,将该样本归到距离最短的中心所在的类。
3)利用均值等方法更新该类的中心值;
4)对于所有的K个聚类中心,如果利用(2)(3)的迭代法更新后,值保持不变,则迭代结束,否则继续迭代。
5)对同一类簇中的对象相似度极高,不同类簇中的数据相似度极低。
图6-21为聚类结果示意图。
图6-21 k-means聚类示意图
对k均值算法,如果原数据很多,其计算量非常大,对于大数据是否有更好的方法呢?每次处理聚类算法时,采用少批量而不是所有数据进行训练,Scikit-learn提供的小批量k均值(Mini Batch K-Means)算法,这种方法非常高效,在深度学习计算梯度下降时,经常采用类似方法,称为随机梯度下降法,具体内容第7章将介绍。
6.4 数据预处理
特征工程是机器学习任务中一项重要内容,而数据预处理又是特征工程的核心内容,本节将介绍基于Python、Pandas及Sklearn的几种数据预处理工具。
首先,我们简单介绍机器学习中经常出现的特征工程中数据预处理,然后,用葡萄酒数据集实现一个完整的机器学习任务。
6.4.1 处理缺失值
机器学习中经常遇到缺失值的情况,遇到缺失数据,如果简单的删除,可能因此删除一些有用信息,更重要的可能删除数据的历史轨迹。所以,我们往往采用补填方式进行处理。补填的方法很多,如用0补填,用所在列的平均数、中位数、自定义数等补填,或缺失值的相邻项进行补填等。以下说明如何用所在列的平均数来补填缺失数据。
|
1 2 3 4 5 6 7 8 9 10 |
import pandas as pd from io import StringIO csv_data = '''A,B,C,D 1.0,2.0,3.0,4.0 5.0,6.0,,8.0 10.0,11.0,12.0,''' df = pd.read_csv(StringIO(csv_data)) df |
结果显示:
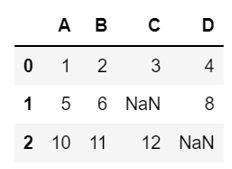
查看有缺失值的个数及对应列。
|
1 |
df.isnull().sum() |
A 0
B 0
C 1
D 1
dtype: int64
说明C、D列各有一个缺失值。用缺失值所在列的平均值补填。
|
1 2 3 4 5 6 |
from sklearn.preprocessing import Imputer imr = Imputer(missing_values='NaN', strategy='mean', axis=0) imr = imr.fit(df) imputed_data = imr.transform(df.values) imputed_data |
运行结果:
array([[ 1. , 2. , 3. , 4. ],
[ 5. , 6. , 7.5, 8. ],
[ 10. , 11. , 12. , 6. ]])
6.4.2 处理分类数据
机器学习的数据集中往往包含很多分类数据,其中有些是有序的(即有大小的区别,如衣服的型号,M<X<XL),有些是无序的(即没有大小的区别,如表示颜色的类别等)。对这些类别的如果处理不当,进行影响模型性能,尤其涉及几何距离方面的机器学习任务中。为此,我们一般把有序类别直接转换成整数,而把无序类别转换为独热编码。如果把无序类别也转换为整数,如红色转换为1,黄色转换为2,蓝色转换为3等,这样就给颜色类别赋予大小的含义了,实际上颜色应该更大小无关,从而破坏其本来属性。
|
1 2 3 4 5 6 7 8 |
import pandas as pd df = pd.DataFrame([ ['green', 'M', 10.1, 'class1'], ['red', 'L', 13.5, 'class2'], ['blue', 'XL', 15.3, 'class1']]) df.columns = ['颜色', '型号', '价格', '类别'] df |
运行结果

把有序特征型号变为整数
|
1 2 3 4 5 6 7 |
size_mapping = { 'XL': 3, 'L': 2, 'M': 1} df['型号'] = df['型号'].map(size_mapping) df |
运行结果
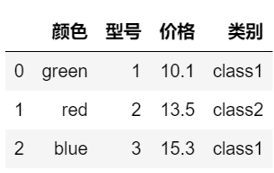
然后把无序特征颜色变为one-hot编码。
|
1 |
pd.get_dummies(df[['价格', '颜色', '型号']]) |
运行结果

主要颜色由1列变为3列,这3列中只有一个1,其余都是0。
【说明】把无序类别数据转换为热编码,对涉及距离计算类算法(如线性回归、KNN等算法)尤其重要要。对概率或比率类算法(如决策树、朴素贝叶斯等算法)直接转换为整数即可,不一定需要转换为热编码。
6.5 机器学习实例
这里以葡萄酒(wine)数据集为例,因数据集不大,可以直接从网上下载。
葡萄酒数据集中的数据包括三种酒的13种不同成分的数量。文件中,每行代表一种酒的样本,共有178个样本;一共有14列,其中,第一个属性是类标识符,分别是1/2/3来表示,代表葡萄酒的三个分类。后面的13列为每个样本的对应属性的样本值。剩余的13个属性是,酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调、稀释葡萄酒的OD280/OD315、脯氨酸。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。 具体属性描述如表6-3所示。
表6-3 葡萄酒数据集属性
| 英文字段 | 中文字段 |
| Class label | 类别 |
| Alcohol | 酒精 |
| Malic acid | 苹果酸 |
| Ash | 灰 |
| Alcalinity of ash | 灰的碱度 |
| Magnesium | 镁 |
| Total phenols | 总酚 |
| Flavanoids | 类黄酮 |
| Nonflavanoid phenols | 非类黄酮酚 |
| Proanthocyanins | 原花青素 |
| Color intensity | 色彩强度 |
| Hue | 色调 |
| OD280/OD315 of diluted wines | 稀释酒的OD280 / OD315 |
| Proline | 脯氨酸 |
1)从网上下载数据。
|
1 2 3 4 5 6 7 8 9 10 11 |
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None) df_wine.columns = ['类别', '酒精', '苹果酸', '灰', '灰的碱度', '镁', '总酚', '类黄酮', '非类黄酮酚', '原花青素', '色彩强度', '色调', '稀释酒的OD280 / OD315', '脯氨酸'] #查看共有哪几种类别 print('类别', np.unique(df_wine['类别'])) #查看数据集前5行 df_wine.head() |
运行结果如下:
类别 [1 2 3]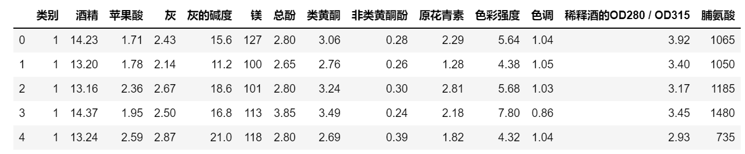
2)对数据进行标准化处理。
|
1 2 3 4 5 |
from sklearn.preprocessing import StandardScaler stdsc = StandardScaler() X_train_std = stdsc.fit_transform(X_train) X_test_std = stdsc.transform(X_test) |
3)使用逻辑回归进行训练。
|
1 2 3 4 5 6 |
from sklearn.linear_model import LogisticRegression lr = LogisticRegression(penalty='l1', C=0.1,solver='liblinear') lr.fit(X_train_std, y_train) print('Training accuracy:', lr.score(X_train_std, y_train)) print('Test accuracy:', lr.score(X_test_std, y_test)) |
运行结果如下:
Training accuracy: 0.9838709677419355
Test accuracy: 0.9814814814814815
说明准确率还不错。
4)可视化各特征的权重系统。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['font.sans-serif']=['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False fig = plt.figure() ax = plt.subplot(111) colors = ['blue', 'green', 'red', 'cyan', 'magenta', 'yellow', 'black', 'pink', 'lightgreen', 'lightblue', 'gray', 'indigo', 'orange'] weights, params = [], [] for c in np.arange(-4, 6): lr = LogisticRegression(penalty='l1', C=10.**c, solver='liblinear',random_state=0) lr.fit(X_train_std, y_train) weights.append(lr.coef_[1]) params.append(10.**c) weights = np.array(weights) for column, color in zip(range(weights.shape[1]), colors): plt.plot(params, weights[:, column], label=df_wine.columns[column+1], color=color) plt.axhline(0, color='black', linestyle='--', linewidth=3) plt.xlim([10**(-5), 10**5]) plt.ylabel('权重系数') plt.xlabel('C') plt.xscale('log') plt.legend(loc='upper left') ax.legend(loc='upper center', bbox_to_anchor=(1.38, 1.03), ncol=1, fancybox=True) # plt.savefig('./figures/l1_path.png', dpi=300) plt.show() |
运行结果如图6-22所示。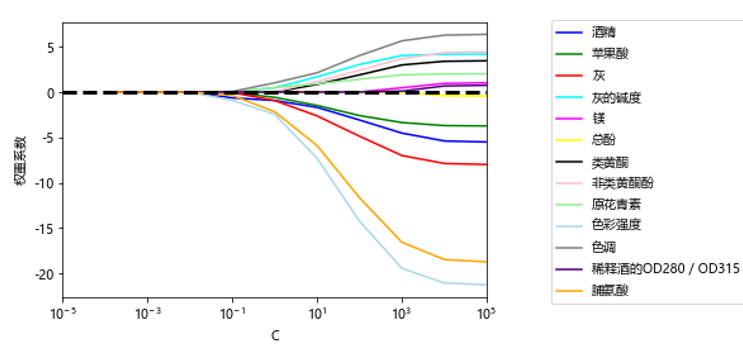
图6-22 各特征随着惩罚系数c变化的情况
5)查看选择的特征数量与模型的准确率的关系。先来定义数据预处理函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
from sklearn.base import clone from itertools import combinations import numpy as np from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score class SBS(): def __init__(self, estimator, k_features, scoring=accuracy_score, test_size=0.25, random_state=1): self.scoring = scoring self.estimator = clone(estimator) self.k_features = k_features self.test_size = test_size self.random_state = random_state def fit(self, X, y): X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=self.test_size, random_state=self.random_state) dim = X_train.shape[1] self.indices_ = tuple(range(dim)) self.subsets_ = [self.indices_] score = self._calc_score(X_train, y_train, X_test, y_test, self.indices_) self.scores_ = [score] while dim > self.k_features: scores = [] subsets = [] for p in combinations(self.indices_, r=dim-1): score = self._calc_score(X_train, y_train, X_test, y_test, p) scores.append(score) subsets.append(p) best = np.argmax(scores) self.indices_ = subsets[best] self.subsets_.append(self.indices_) dim -= 1 self.scores_.append(scores[best]) self.k_score_ = self.scores_[-1] return self def transform(self, X): return X[:, self.indices_] def _calc_score(self, X_train, y_train, X_test, y_test, indices): self.estimator.fit(X_train[:, indices], y_train) y_pred = self.estimator.predict(X_test[:, indices]) score = self.scoring(y_test, y_pred) return score |
可视化特征数与准确率之间的关系。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
%matplotlib inline from sklearn.neighbors import KNeighborsClassifier import matplotlib.pyplot as plt knn = KNeighborsClassifier(n_neighbors=2) # 选择特征 sbs = SBS(knn, k_features=1) sbs.fit(X_train_std, y_train) # 可视化特征子集的性能 k_feat = [len(k) for k in sbs.subsets_] plt.plot(k_feat, sbs.scores_, marker='o') plt.ylim([0.7, 1.1]) plt.ylabel('Accuracy') plt.xlabel('Number of features') plt.grid() plt.tight_layout() # plt.savefig('./sbs.png', dpi=300) plt.show() |
运行结果如图6-23所示。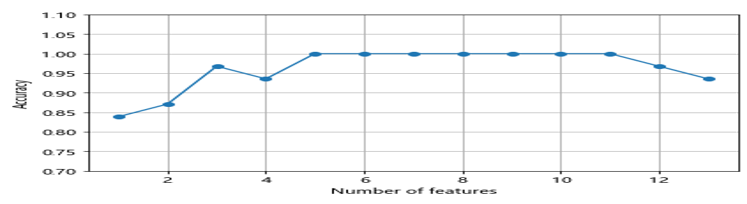
图6-23 特征数与准确率之间的关系
6)可视化各特征对模型的贡献率。使用随机森林算法,计算特征对模型的贡献。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
from sklearn.ensemble import RandomForestClassifier feat_labels = df_wine.columns[1:] forest = RandomForestClassifier(n_estimators=10000, random_state=0, n_jobs=-1) forest.fit(X_train, y_train) importances = forest.feature_importances_ indices = np.argsort(importances)[::-1] for f in range(X_train.shape[1]): print("%2d) %-*s %f" % (f + 1, 30, feat_labels[f], importances[indices[f]])) plt.title('Feature Importances') plt.bar(range(X_train.shape[1]), importances[indices], color='lightblue', align='center') plt.xticks(range(X_train.shape[1]), feat_labels, rotation=45) plt.xlim([-1, X_train.shape[1]]) plt.tight_layout() # plt.savefig('./figures/random_forest.png', dpi=300) plt.show() |
运行结果如图6-24所示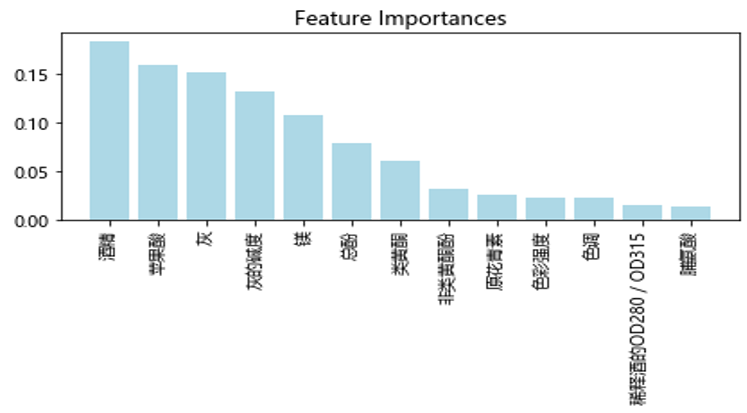
图6-24 各特征的贡献率
说明酒精这个特征贡献最大,其次是苹果酸、灰等特征。
6.6 小结
机器学习是深度学习的基础,机器学习的很多方法在深度学习中得到进一步拓展,如机器学习中正则化方法、核函数、优化方法等在深度学习中都有。本章主要介绍机器学习的基本原理,为深度学习打下一个基础。