第7章带约束的优化问题

带约束条件的最优化问题，约束条件一般分为两种，一种是等式约束；另一种是不等式约束。对于第一种等式约束的优化问题，可以直接利用拉格朗日乘子法去获得最优解；对于不等式约束的优化问题，可以转化为Karush–Kuhn–Tucker conditions（KKT条件）下应用拉格朗日乘数法求解。两种情况都应用拉格朗日乘数法，给出优化问题的必要条件。

7.1 拉格朗日乘数法

拉格朗日乘数法(又称为拉格朗日乘子法)，就是求函数f(x_1,x_2,\cdots,x_n)在等式约束函数h(x_1,x_2,\cdots,x_n)=0或不等式约束函数g(x_1,x_2,\cdots,x_n)\le 0的约束条件下的极值的方法。其主要思想是引入一个新的参数λ（即拉格朗日乘子），将约束条件函数与原函数联系到一起，配成与变量数量相等的等式方程，从而求出原函数极值的必要条件。
假设向量x= (x_1,x_2,\cdots,x_n)，目标函数为f(x),等式约束函数为h(x),不等式约束函数为g(x)
求等式约束条件下的极值问题：
\underset{\rm x}{min}f(\rm{x})
s.t.h(\rm x)
利用拉格朗日乘数法构造拉格朗日乘子函数：
L(\rm x,u)=f(\rm x)+uh(\rm x) \tag{7.1}
其中参数u称为拉格朗日乘子。利用拉格朗日乘数法把有约束的极值问题，转换为无约束的极值问题。对拉格朗日乘子函数的所有自变量（x及参数u）求导，并令其为0，就可得到函数的候选极值点。
\nabla_{\rm x} L(\rm x,u)=\nabla_{\rm x} f(\rm x)+u\nabla_{\rm x} h(\rm x)=0 \tag{7.2}
\nabla_u L(\rm x,u)=h(\rm x)=0 \tag{7.3}
由式（7.2）可知，在极值点目标函数的梯度是约束函数梯度的倍数，即这两个梯度是平行的关系，如图7-1所示。如果有多个等式约束函数，目标函数的梯度是约束函数梯度的线性组合。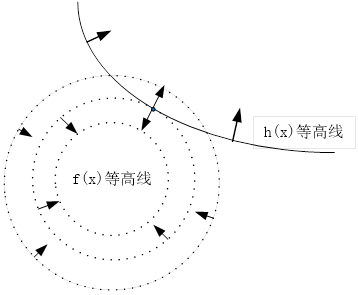

图7-1 f(x)的等高线与约束函数h(x)等高线在切点的梯度互相平行
【说明】f(x)的梯度是等高线的法向量。以二维空间为例，假设而为函数f(x,y)
根据微分定义：
f(x+\Delta x,y+\Delta y)\approx f(x,y)+\frac{\partial f}{\partial x}\Delta x+\frac{\partial f}{\partial y}\Delta y=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\left(\begin{matrix}\Delta x\\ \Delta y\end{matrix}\right)
(\Delta x,\Delta y)表示函数f(x)等高线的方向，当\Delta x \longrightarrow 0,\Delta y \longrightarrow 0时，(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})\left(\begin{matrix}\Delta x\\ \Delta y\end{matrix}\right)\longrightarrow 0
即等高线的方向与f(x)的梯度互相垂直。
例1：利用拉格朗日乘数法求如下极值问题
\underset{x,y}{min}(x^2+y^2)
s.t. xy-3=0
（1）构建拉格朗日乘子函数
L(x,y,u)=x^2+y^2+u(xy-3)
对自变量及乘子变量求导，并令其为0，可得如下方程组：
\frac{\partial L}{\partial x}=2x+uy=0
\frac{\partial L}{\partial y}=2y+ux=0
\frac{\partial L}{\partial u}=xy-3=0
解得：
u=-2,x=\sqrt 3,y=\sqrt 3或x=-\sqrt 3,y=-\sqrt 3
目标函数(x^2+y^2)的海塞矩阵为：
\left(\begin{matrix}{\frac{\partial^2 f}{\partial x^2}}&{\frac{\partial^2 f}{\partial x{\partial y}}}\\{\frac{\partial^2 f}{\partial y{\partial x}}}&{\frac{\partial^2 f}{\partial y^2}}\end{matrix}\right)=\left(\begin{matrix}{2}&0 \\ {0}&2\end{matrix}\right)
为正定矩阵，故目标函数是凸函数，有极小值。极值点与等高线之间的位置见图7-2所示

图7-2 极值点的位置示意图
实现图72-的python代码：

求不等式约束条件下的极值问题：
前面介绍了等式约束的极值问题，通常面对更多的是不等式条件约束的情况，对这种情况，其取得极值的必要条件为KKT条件（非充分条件，如果优化问题为优化问题，则是充分条件）。
\underset{\rm x}{min}f(\rm{x})
s.t. g(\rm x)\leq 0
利用拉格朗日乘数法构造拉格朗日乘子函数：
L(\rm x,\lambda)=f(\rm x)+\lambda g(\rm x)
其中参数\lambda称为拉格朗日乘子，g(\rm x)\leq 0
对不等式约束，极值点与不等式构成的区域有2种情况，如图7-3所示。
（1）极值点在g(x)<0区域内，如图7-3（a），这就是没有限制条件下的极值点，不等式约束不起作用，可以直接最小化目标函数，求得极值点x^*，由此可得：
\nabla_{x^*} f(x^*)=0,\lambda=0,g(x^* )<0

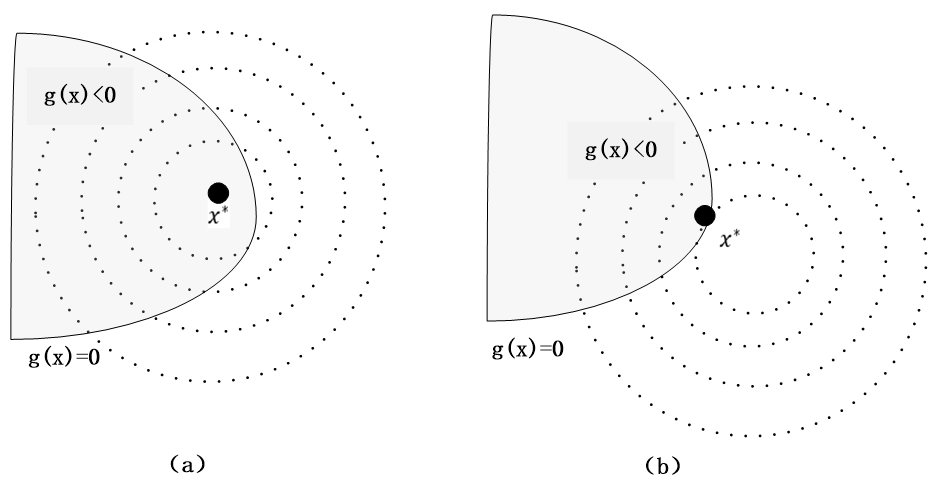
图7-3  极值点在约束区域的位置

（2）极值点在g(x)=0上，如图7-3（b）所示。 这种情况，约束条件起作用，所以\lambda \neq 0，g(x)=0。这样问题就相当于等式约束问题，由此可得极值点满足： \nablaf(x^* )=-\lambda\nabla g(x^*) 由图7-1可知，梯度\nabla f(x)与梯度\nabla g(x)平行且方向相反，为此需要\lambda > 0,即有：
g(x^* )=0,\lambda > 0
综合以上两种情况，就得到在不等式约束的条件下，获取极值点的必要条件为：
\lambda \geq 0,\lambda g(x^*)=0,g(x^* )\leq 0
这实际上就是KKT条件的核心内容。
接下来简单介绍KKT条件的完整信息。

例2：求下例问题的极值

目标函数为凸函数，解得最小值为：x=y=1
目标函数最优点的位置如图7-4所示。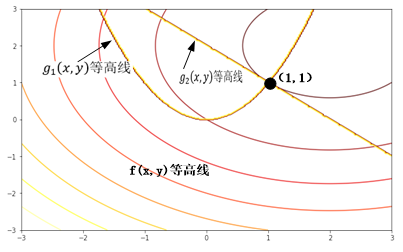

图7-4 目标函数与约束函数等高线及最优点位置

7.2 KKT条件

KKT条件是求带等式、不等式约束问题极值的一阶必要条件，是拉格朗日乘数法的推广，对于如下的优化问题：

【说明】KKT条件只是取得极值的必要条件，而非充分条件。如果是一个凸优化问题，KKT条件是取得极值的充分必要条件。