3.3 连续型随机变量及分布

文章目录

3.3 连续型随机变量及分布
3.3.1 连续型随机变量及分布概述
3.3.2 均匀分布
3.3.3 指数分布
3.3.4 正态分布

如果X由全部实数或者由一部分区间组成，如：
X={x| a≤x≤b},其中a<b,它们都为实数。
则称 X为连续随机变量，连续随机变量的取值是不可数及无穷尽的。

3.3.1 连续型随机变量及分布概述

与离散型随机变量不同，连续型随机变量采用概率密度函数来描述变量的概率分布。如果一个函数f(x)是密度函数，满足以下三个性质，我们就称f(x)为概率密度函数。
（1） $f(x)\geq 0$ ,注意这里不要求 $f(x)\leq 1$ 。
（2） $\int_{-\infty}^{\infty}f(x)dx=1$ 。
（3）对于任意实数 $x_1$ 和 $x_2$ ，且 $x_1\leq x_2$ ,有：
$P(x_1\lt X\leq x_2)=\int_{x_1}^{x_2}f(x)dx \tag{3.3}$
第（2）个性质表明，概率密度函数f(x)与x轴形成的区域的面积等于1，第（3）个性质表明，连续随机变量在区间 $[x_1,x_2]$ 的概率等于密度函数在区间 $[x_1,x_2]$ 上的积分，也即是与X轴在 $[x_1,x_2]$ 内形成的区域的面积，如图3-3所示。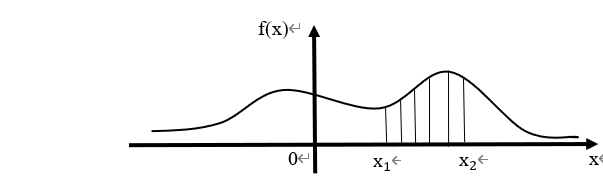
图3-3 概率密度函数
对连续型随机变量在任意一点的概率处处为0。
假设有任意小的实数 $\Delta x$ ，由于 $\{X=x\}\subset\{x-\Delta x<X\leq x\}$ ,由式（4.1）分布函数的定义可得：
$0\leq P(X=x)\leq P(x-\Delta x<X\leq x)=F(x)-F(x-\Delta x)\tag{3.4}$
令 $\Delta x\rightarrow 0$ ,由夹逼准则，式（3.4）可求得：
$P(X=x)=0 \tag{3.5}$
式（3.5）表明，对于连续型随机变量，它在任意一点的取值的概率都为0。因此，在连续型随机变量中，当讨论区间的概率定义时，一般对开区间和闭区间不加区分，即：
$P(x_1\leq X\leq x_2)=P(x_1<X\leq x_2)=P(x_1\leq X<x_2)=P(x_1<X<x_2)$ 成立。

3.3.2 均匀分布

若连续型随机变量X具有概率密度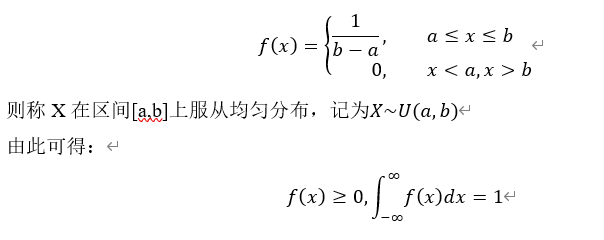

3.3.3 指数分布

若连续型随机变量X的概率密度为
$f(x)=\begin{cases}\frac{1}{\theta}e^{\frac{-x}{\theta}},&x>0\\0,&x\leq 0)\end{cases}$
其中 $\theta >0$ 为常数，则称X服从参数为θ的指数分布。

3.3.4 正态分布

若连续型随机变量X的密度函数为：
其中 $\mu$ 是平均值， $\sigma$ 是标准差（何为平均值、标准差后续我们会介绍）。这个连续分布被称之为正态分布，或者高斯分布。其密度函数的曲线呈对称钟形，因此又被称之为钟形曲线，正态分布是一种理想分布，记为 $X\sim N(\mu,{\sigma}^2)$

正态分布如何用Python实现呢？同样，我们可以借助其scipy库中stats来实现，非常方便。

import numpy as np
import matplotlib.pyplot as plt 
from scipy import stats  
%matplotlib inline

#平均值或期望值
mu=0     
#标准差
sigma1=1 
sigma2=2 

#随机变量的取值
x=np.arange(-6,6,0.1)
y1=stats.norm.pdf(x,0,1) #定义正态分布的密度函数
y2=stats.norm.pdf(x,0,2) #定义正态分布的密度函数
plt.plot(x,y1,label='sigma is 1')
plt.plot(x,y2,label='sigma is 2')
plt.title('normal $\mu$=%.1f,$\sigma$=%.1f or %.1f '%(mu,sigma1,sigma2))
plt.xlabel('x')
plt.ylabel('probability density')
plt.legend(loc='upper left')
plt.show()

import numpy as np

import matplotlib.pyplot as plt

from scipy import stats

%matplotlib inline

#平均值或期望值

mu=0

#标准差

sigma1=1

sigma2=2

#随机变量的取值

x=np.arange(-6,6,0.1)

y1=stats.norm.pdf(x,0,1) #定义正态分布的密度函数

y2=stats.norm.pdf(x,0,2) #定义正态分布的密度函数

plt.plot(x,y1,label='sigma is 1')

plt.plot(x,y2,label='sigma is 2')

plt.title('normal $\mu$=%.1f,$\sigma$=%.1f or %.1f '%(mu,sigma1,sigma2))

plt.xlabel('x')

plt.ylabel('probability density')

plt.legend(loc='upper left')

plt.show()

sigmal系统与正态分布如图3-4所示。

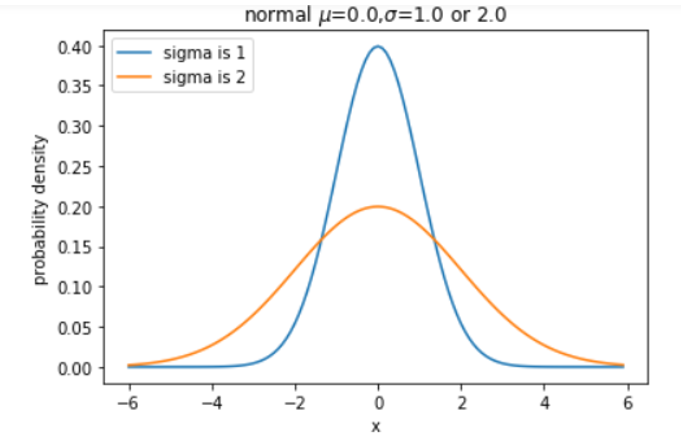
图3-4 sigmal系统与正态分布
正态分布的取值可以从负无穷到正无穷。这里我们为便于可视化，只取把X数据定义在[-6,6]之间，用stats.norm.pdf得到正态分布的概率密度函数。另外从图形可以看出，上面两图的均值 $\mu$ 都是0，只是标准差 $(\sigma)$ 不同，这就导致图像的离散程度不同，标准差大的更分散，个中原因，我们在介绍随机变量的数字特征时将进一步说明。