第4章极限定理

文章目录

第4章极限定理
4.1 切比雪夫不等式
4.2 大数定律
4.3 中心极限定理
4.4 极限定理实例

4.1 切比雪夫不等式

切比雪夫不等式可以对随机变量偏离期望值的概率做出估计，这是推导大数定律的基础。
假设随机变量X的数学期望为 $\mu$ ,标准差为 $\sigma$ ，则对任意的 $\varepsilon>0$ ,有:
$p(|x-\mu|\ge\varepsilon)\le \frac{\sigma^2}{\varepsilon^2}\tag{4.1}$
切比雪夫不等式的直观解释是随机变量离数学期望越远（即 $\varepsilon$ 越大），落入该区域的概率越小。下面进行证明，对于连续型随机变量，概率密度函数为p(x),则
$p(|x-\mu|\ge\varepsilon)=\int_{-\infty}^{\mu-\varepsilon} p(x)dx+\int_{\mu+\varepsilon}^{\infty} p(x)dx\tag{4.2}$
式（4.2）所求的就是图4-1中阴影部分的面积。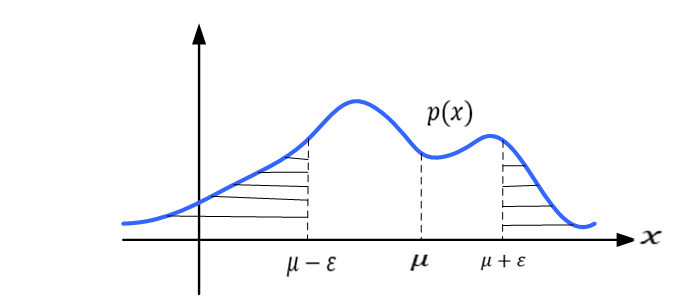
图4-1 切比雪夫不等式计算示意图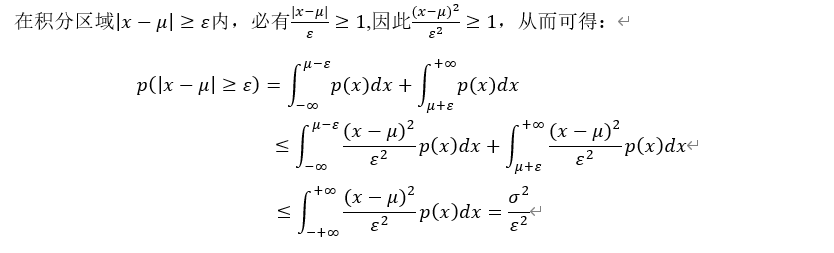

4.2 大数定律

大数定律是一种描述当试验次数很大时所呈现的概率性质的定律。但是注意到，大数定律并不是经验规律，而是在一些附加条件上经严格证明了的定理，它是一种自然规律因而通常不叫定理而是大数“定律”。
具体而言, 大数定律表明, 对一列独立同分布的随机变量而言, 当随机变量的个数 $n\to\infty$ 时, 其均值几乎必然收敛于其期望。这种偶然中包含着某种必然的规律,就称为大数定律。
1、切比雪夫大数定律：
假设有一组互相独立的随机变量： $X_1,X_2,\cdots,X_n$ ，它们的方差 $var[X_i]$ 均存在且有公共上界，即 $var[X_i ]<C,i=1,2,\cdots,n$ ,它们的均值为： $\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i$ 则对任意的 $\varepsilon>0$ ，有：
$\lim_{n\to\infty}p\left(\left|\bar{X}-\frac{1}{n}\sum_{i=1}^n E[X_i]\right|<\varepsilon\right)=1$
大数定律描述了大量重复试验的结果，即结果的平均值应接近预期值，并随着试验次数的增加，结果将趋于预期值。
证明如下：
均值X ̅的数学期望为：
$E[\bar{X}]=\frac{1}{n}\sum_{i=1}^n E[X_i]$
由于随机变量 $X_1,X_2,\cdots,X_n$ 互相独立，且有公共上界，因此它们均值得方差满足：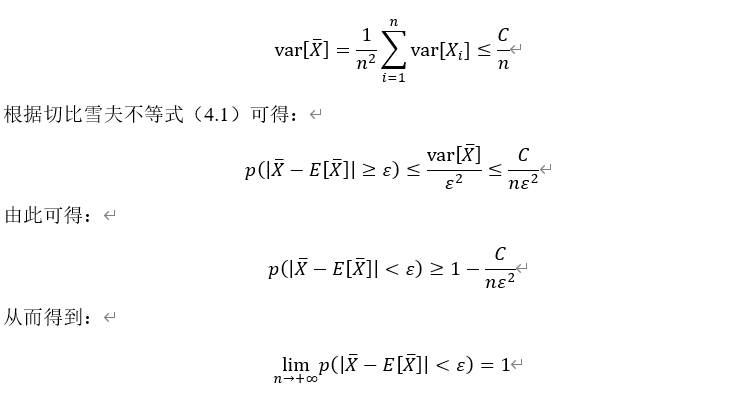
大数定律告诉我们，随机事件重复发生后，其可能性结果会趋于一种稳定的状态。它揭示了随机事件发生频率的长期稳定性，体现了偶然之中包含一种必然。

4.3 中心极限定理

大数定律说明随机变量的平均值X以概率收敛于期望值，中心极限定理则进一步说明X收敛于何种分布。
中心极限定理的主要思想：如果随机变量: $X_1,X_2,\cdots,X_n$ 满足一定条件，当n足够大时，X ̅近似服从正态分布。因此，在机器学习与深度学习中，通常假设随机变量服从正态分布，背后的理论基础就是中心极限定理。
此定理只是被称作极限定理. 随着人们发现它在概率论中有着极为重要的位置, 才把它称之为中心极限定理。
林德贝格-勒维（Lindeberg-Levy）中心极限定理，又称为独立同分布中心极限定理。
设随机变量 $\{X_i\},i=1,\cdots,n$ 独立同分布，数学期望为 $\mu$ ，方差为 $\sigma^2>0$ ，它们的均值：
$\bar{X}=\frac{1}{n}\sum_{i=1}^n X_i$
$\bar{X}$ 的数学期望为 $E[\bar{X}]=\mu$ ,方差 $var[\bar{X}]=\frac{\sigma^2}{n}$ ,对随机变量的均值进行归一化处理：
$\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$
则有：
$\lim_{n \to \infty}p\left(\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}<x\right)=\int_{-\infty}^{x} \frac{1}{\sqrt{2\pi}} e^{\frac{- t^2}{2}}dt=\Phi(x)$
其中 $\Phi(x)$ 为标准正态分布的分布函数。
中心极限定理的应用之一：在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体。
大数定律和中心极限定理可以看做随机变量的零阶和一阶“泰勒展开”，其中大数定律是随机变量的“零阶估计”，中心极限定理是在大数定律成立下的“一阶导数”，在极限下高阶小量可忽略。

4.4 极限定理实例

假设我们现在观测一个人掷骰子。这个骰子是公平的，也就是说掷出1~6的概率都是1/6,这是一个典型的独立同分布的试验，我们来模拟大数定律和中心极限定理的作用。
1、生成数据

import numpy as np 
import seaborn as sns

np.random.seed(101)
random_data = np.random.randint(1, 7, 10000)
print(random_data.mean())  #均值
print(random_data.std())   #标准差

import numpy as np

import seaborn as sns

np.random.seed(101)

random_data = np.random.randint(1, 7, 10000)

print(random_data.mean()) #均值

print(random_data.std()) #标准差

3.5023
1.7011
平均值接近3.5很好理解。因为每次掷出来的结果是1、2、3、4、5、6。每个结果的概率是1/6。所以加权平均值就是3.5
2、可视化生成数据
我们把生成的数据用直方图画出来，看随机生成的各个数的统计情况。

sns.distplot(random_data,color='blue',bins=6)

1	sns.distplot(random_data,color='blue',bins=6)

图4-2 随机数构成的直方图
从图4-2可以看出，各个数的总数基本相同，差别不大。
3、抽一组抽样来试试
从生成的数据中随机抽取10个数字,不放回的方式可以看到，我们只抽10个的时候，样本的平均值（3.1）会距离总体的平均值（3.5）有所偏差。有时候我们运气不好，抽出来的数字可能偏差可能更大。

samples=np.random.choice(random_data,10,replace=False)
print(samples)         #这10个随机抽取的数字
print(samples.mean())  #均值

samples=np.random.choice(random_data,10,replace=False)

print(samples) #这10个随机抽取的数字

print(samples.mean()) #均值

[2 2 4 5 2 3 4 2 6 1]
3.1

如果随机抽取1000个数，其平均值为 3.489非常接近其期望值3.5.这验证了大数定律的强大。

samples1=np.random.choice(random_data,1000,replace=False)
print(samples1.mean())  #均值

1 2	samples1=np.random.choice(random_data,1000,replace=False) print(samples1.mean()) #均值

4、中心极限定理发挥作用
现在我们抽取1000组，每次在原随机向量的基础上加一个随机数。每组的平均值构成一个随机变量序列 $\{\bar{X}_i,i=1,2,\cdots,1000\}$ ，该序列的分布近似正态分布

samples = []
samples_mean = []
samples_std = []
for i in range(0, 1000):
    samples = list(samples)
    samples.append(np.random.choice(random_data,1,replace=False))
    samples=np.array(samples)
    samples_mean.append(samples.mean())

sns.distplot(samples_mean,bins=30,color='blue')

samples = []

samples_mean = []

samples_std = []

for i in range(0, 1000):

samples = list(samples)

samples.append(np.random.choice(random_data,1,replace=False))

samples=np.array(samples)

samples_mean.append(samples.mean())

sns.distplot(samples_mean,bins=30,color='blue')

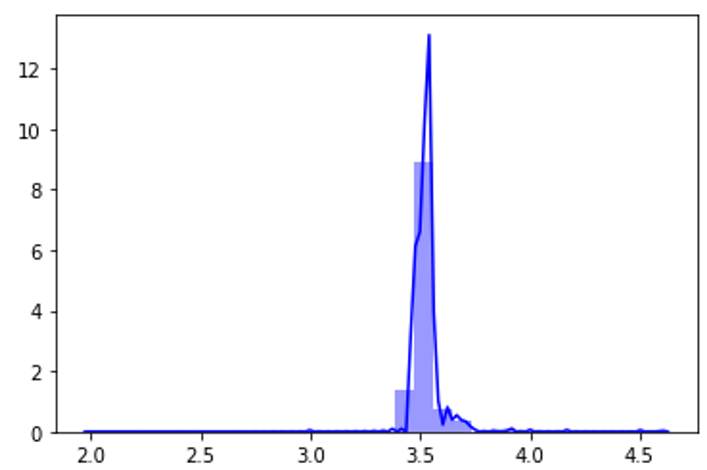
图4-3 序列的分布近似正态分布