5.3.4 EM算法推导
通过构建目标函数的下界函数来处理隐含变量的似然函数,该下界函数更容易优化,并通过求解下界函数的极值,构造新的下界函数,通过迭代的方法,使下界函数收敛于局部最优值。
假设概率分布 生成可观察样本为
生成可观察样本为 ,这n个样本互相独立,以及无法观察的隐含数据为
,这n个样本互相独立,以及无法观察的隐含数据为 构成完整数据,样本的模型参数为
构成完整数据,样本的模型参数为 。完整数
。完整数 的似然函数为:
的似然函数为:
下界函数通过隐变量的概率分布构造,对每个样本 ,假设
,假设 为隐变量
为隐变量 的一个概率密度函数,它们满足概率的规范性,即有:
的一个概率密度函数,它们满足概率的规范性,即有:

利用隐变量的概率分布,对原来的对数似然函数进行恒等变形。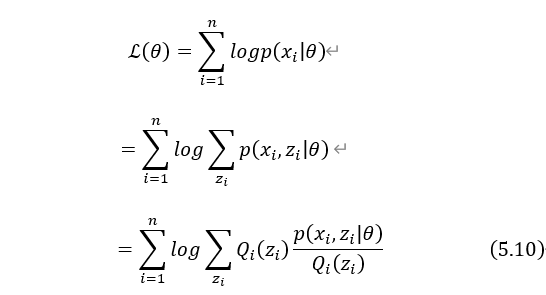
根据随机变量函数的数学期望的定义可得: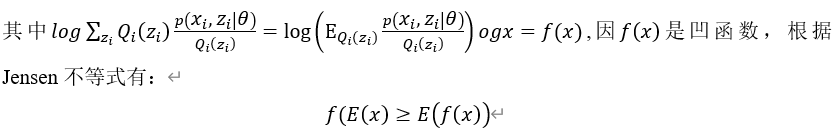
把数学期望E看成是关于 概率的期望,由式(5.10)可得:
概率的期望,由式(5.10)可得: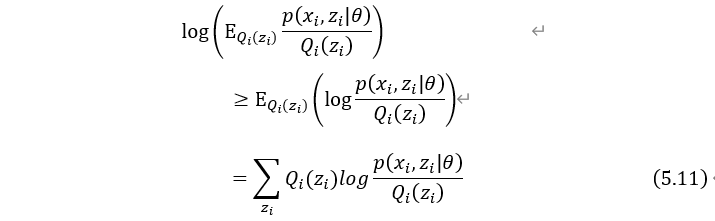
由式(5.10)、(5.11)可得: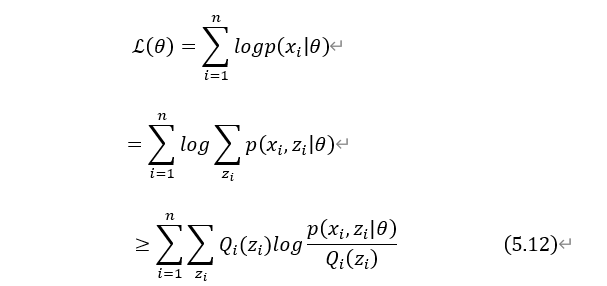
式(5.12)为似然函数 下界函数,满足条件的下界函数有很多。因为EM是迭代算法,并且是求下界函数的极值点来找到下一步迭代的参数
下界函数,满足条件的下界函数有很多。因为EM是迭代算法,并且是求下界函数的极值点来找到下一步迭代的参数 ,设
,设 为第t次迭代时参数的估计值。
为第t次迭代时参数的估计值。
如何取在 处下界函数?当然与似然函数
处下界函数?当然与似然函数 越接近越好,所以我们希望(5.12)式在
越接近越好,所以我们希望(5.12)式在 这个点能取等号。由Jensen不等式可知,等式成立的条件是随机变量是常数,故在
这个点能取等号。由Jensen不等式可知,等式成立的条件是随机变量是常数,故在 点处有:
点处有:
所以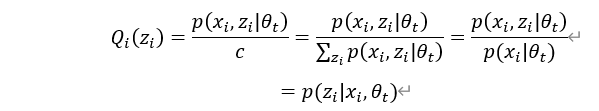
由此可知, 实际上就是隐变量
实际上就是隐变量 的后验概率
的后验概率 。
。
用 表示
表示 代入
代入  的下界函数中,得:
的下界函数中,得: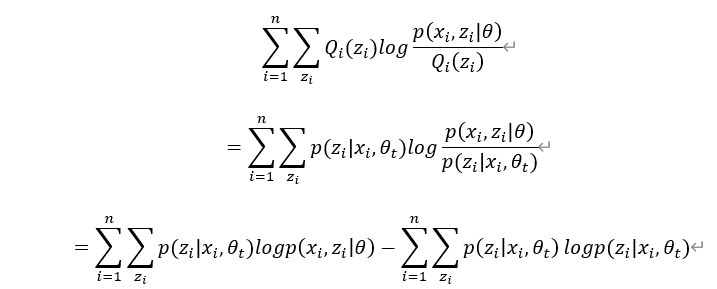
对 的下界函数中求极大值为下次迭代的参数值
的下界函数中求极大值为下次迭代的参数值 ,即有:
,即有:
到这来EM算法的推导就结束了。
下面给出EM算法的具体步骤:
(1) 初始化参数 ,然后开始循环迭代,第t次迭代的分为两步,即E步和M步。
,然后开始循环迭代,第t次迭代的分为两步,即E步和M步。
(2) E步:
基于当前参数估计值 ,构建目标函数。
,构建目标函数。
具体包括计算给定样本时对隐变量z的条件概率,即

然后计算 函数。
函数。
(3) M步
求 函数的极大值,更新参数为
函数的极大值,更新参数为 .
.

迭代第(2)和(3)步,直到参数 收敛或到指定的阈值。
收敛或到指定的阈值。