Python技术交流与分享

第13 章 循环神经网络

13.1 循环神经网络简介

前面介绍卷积神经网络模型主要用于处理网格化数据，而且预先假设输入数据之间是互相独立的。但在很多实际应用中，数据之间是互相依赖的。比如，当我们在理解一句话意思时，孤立的理解这句话的每个词是不够的，我们需要处理这些词连接起来的整个序列；当我们思考问题时，我们都是根据以往的经验和知识，再结合当前的实际情况来综合考虑的。像处理这些有顺序有关的问题，如果用前馈神经网络（如卷积神经网络），会有很大的局限性。为解决这类问题，就诞生了时序神经网络（循环神经网络和递归神经网络）。
这章我们主要介绍循环神经网络，循环神经网络（Recurrent Neural Networks，简称为RNN）是目前非常流行的神经网络模型，在自然语言处理的很多任务中已经展示出卓越的效果。
循环神经网络的发展并不顺利，自从20世纪80年代以来，人们不断优化，出现了很多RNN的变种，由于受当时计算能力的限制，都没有得到广泛的应用。不过随着计算能力的不断提升，近年来情况大有改观。随着一些重要架构的出现，尤其在2006年提出的LSTM，RNN已经有非常强大的应用，能够很好地完成许多领域的序列任务，在语音识别、机器人翻译、人机对话、语音合成、视频处理等方面大显身手。
RNN有很多变种，我们先介绍一种简单的RNN网络，即Elman循环网络，然后介绍循环神经网络的几种有代表性的升级版，如LSTM、GRC、BiLSTM等。

13.2 Elman神经网络

Elman网络是 J. L. Elman于 1990年首先针对语音处理问题而提出来的, 它是一种典型的局部回归网络( global feed for ward l ocal recurrent)。Elman网络可以看作是一个具有局部记忆单元和局部反馈连接的前向神经网络。Elman网络具有与多层前向网络相似的多层结构。它的主要结构是前馈连接, 包括输入层、 隐含层、 输出层, 其连接权可以进行学习修正;反馈连接由一组“结构 ” 单元构成,用来记忆前一时刻的输出值, 其连接权值是固定的。

13.2.1 Elman结构

我们先回顾一下全连接的神经网络，如下图：

这种神经网络中，隐含层的值只取决于输入的x，而且隐含层的神经元之间是没有关联的。
我们看一简单RNN图形，如下图，它由输入层、一个隐藏层和一个输出层组成。

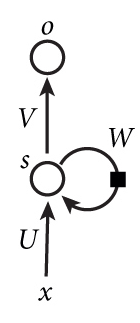
初次看到这个图，很多人会有点头晕，我们通常神经网络，一般是输入-->隐含-->输出，这里隐含层中突然冒出一个带方向的圈，而且上面还标有一个W。这个表示啥意思呢？
其实这个带箭头及W的圈就是循环网络的灵魂，它表示循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x，还取决于上一次隐藏层的值s。权重矩阵 W就是隐藏层上一次的值作为这一次的输入的权重。如果我们把上面的图展开(unfold)，循环神经网络也可以画成下面这个样子：

输入与之前的状态合并为一个向量：


不像传统的深度神经网络，在不同的层使用不同的参数，循环神经网络在所有步骤中共享参数（U、V、W）。这个反映一个事实，我们在每一步上执行相同的任务，仅仅是输入不同。这个机制极大减少了我们需要学习的参数的数量；
上图在每一步都有输出，但是根据任务的不同，这个并不是必须的。例如，当预测一个句子的情感时，我们可能仅仅关注最后的输出，而不是每个词的情感。相似地，我们在每一步中可能也不需要输入。循环神经网络最大的特点就是隐层状态，它可以捕获一个序列的一些信息。

13.2.2 随时间反向传播（BPTT）

前面我们简单介绍RNN的结构，下面我们探讨一下如何找到最好的权值矩阵，或如何对权值矩阵进行优化。对前馈网络，最流行的优化方法是梯度下降法，优化权值矩阵通过反向传播法（BP）,这些方法能在应用在RNN网络吗？当然能，只不过需要对RNN做一点小变化，只要把RNN沿时间轴展开，展开之后便可使用前馈网络一般的方式对RNN进行优化。这样，计算误差相对于各权值的梯度，便可对展开的RNN使用标准的BP方法，因这里涉及一个时间因素，故对RNN来说，这种算法称为随时间反向传播（Back-Propagation Through Time，BPTT）。

我们的优化目标是参数，计算出误差分别对参数U、W、V的梯度，然后用随机梯度下降学习好的参数。像我们汇总这些误差一样，我们也需要汇总一个训练样例在每个时间步(time step)的梯度：

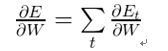
我们可以看到每个时间步长对梯度的贡献。因为W在我们关心的输出的每个步骤中都使用了，所以我们需要将梯度从 网络中一直反向传播到 ，具体过程如下图:

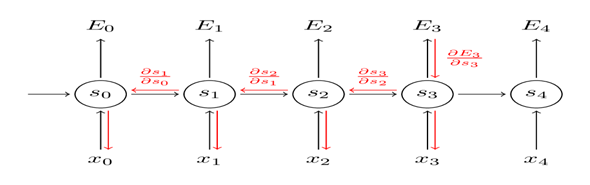
请注意，这与我们在深度前馈神经网络中使用的标准反向传播算法完全相同。关键的区别在于我们汇总了 每个时间步的梯度。在传统的神经网络中，我们不共享层间参数，所以我们不需要汇总任何东西。不过，BPTT只是展开RNN标准反向传播的一个奇特名称。就像Backpropagation一样，我们也可以定义一个向后传递的δ向量，例如：

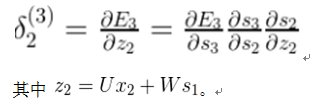
在代码中，一个朴素的BPTT实现如下所示：

从以上代码中易发现，为什么标准RNN比较难训练：序列（句子）可能很长，可能是20个字或更多，因此你需要通过很多层向后传播。在实践中，许多人通过截断方式来限制传播的步数。

13.2.3 梯度消失或爆炸

前面我们提到RNN在学习远程依赖方面存在的问题，这些远程依赖是相隔几个步骤的单词之间的相互作用。这是有问题的，因为英语句子的意思通常是由不太接近的词语来决定的：“头上戴假发的人进去了”。这句话实际上是关于一个人进去，而不是关于假发。但是简单的RNN不可能捕捉到这样的信息。为了理解为什么，让我们仔细看看我们上面计算的梯度：

事实上，上面的雅可比矩阵的2范数的上界为1（其证明大家可以参考相关文档）。而为 （或sigmoid）激活函数将所有值映射到-1和1之间的范围内，并且导数也小于1（而对sigmoid其导数小于1/4），可参考下图：

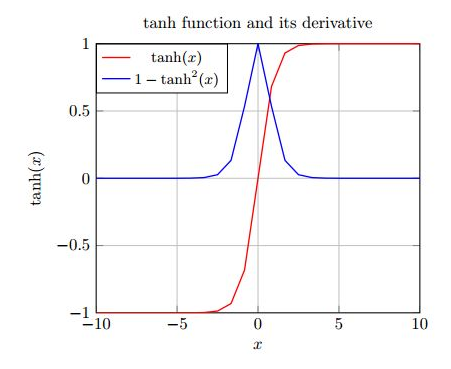
图13.1 tanh函数及其导数图形

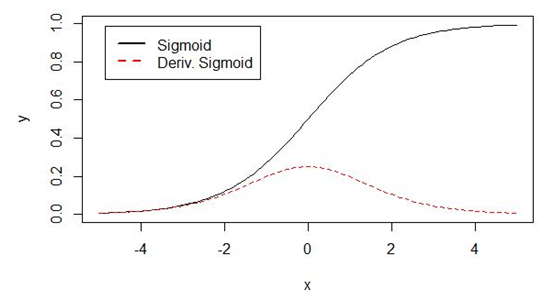
图13.2 sigmoid函数及导数图形

从上图不难看出，tanh(或sigmoid)函数的两端导数逐渐趋于0。最后接近一条水平线。当这种情况出现时，我们就认为相应的神经元饱和了。
它们的梯度为0使得前面层的梯度也为0。矩阵中存在比较小的值，多个矩阵相乘会使梯度值以指数级速度下降，最终在几步后完全消失。比较远的时刻的梯度值为0，这些时刻的状态对学习过程没有帮助，导致你无法学习到长距离依赖。消失梯度问题不仅出现在RNN中，同样也出现在深度前向神经网中。只是RNN通常比较深（例子中深度和句子长度一致），使得这个问题更加普遍。
不难想到，依赖于我们的激活函数和网络参数，如果Jacobian矩阵中的值太大，会产生梯度爆炸而不是梯度消失问题。梯度消失比梯度爆炸受到了更多的关注有两方面的原因。其一，梯度爆炸容易发现，梯度值会变成NaN，导致程序崩溃。
其二，用预定义的阈值裁剪梯度可以简单有效的解决梯度爆炸问题。
梯度消失出现的时候不那么明显而且不好处理。
遇到梯度消失或爆炸是件比较麻烦的事，幸运的是，已经有一些方法解决了梯度消失或爆炸的问题。合适的初始化矩阵W可以减小梯度消失效应，正则化也能起作用。更好的方法是选择ReLU而不是sigmoid和tanh作为激活函数。ReLU的导数是常数值0或1，所以不可能会引起梯度消失。更通用的方案时采用长短项记忆（LSTM）或门限递归单元（GRU）结构。LSTM在1997年第一次提出，可能是目前在NLP上最普遍采用的模型。GRU，2014年第一次提出，是LSTM的简化版本。这两种RNN结构都是为了处理梯度消失问题而设计的，可以有效地学习到长距离依赖，我们会在本章后面部分进行介绍。

13.2.4 循环神经网络扩展

多年来，研究人员开发了更复杂的RNN来处理简单RNN模型的一些缺点。我们将在本章后面的更详细地介绍它们，但是我希望本节能够作为一个简要概述，以便您熟悉模型的分类。

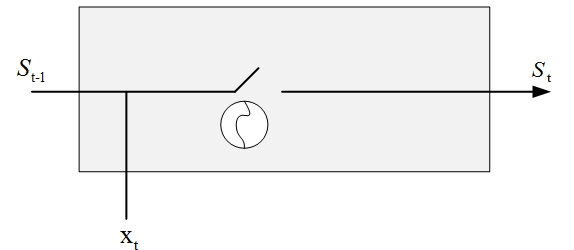
深度（双向）RNN类似于双向RNN，只是在每个时间步有多个层。实际上这给了我们更高的学习能力（但是我们也需要大量的训练数据）。其结构如下：

13.2.5 RNN应用举例

接下来，我们介绍一下基于RNN语言模型。我们首先把词依次输入到循环神经网络中，每输入一个词，循环神经网络就输出截止到目前为止，下一个最可能的词。例如，当我们依次输入：
我 昨天 上学 迟到 了
神经网络的输出如下图所示：

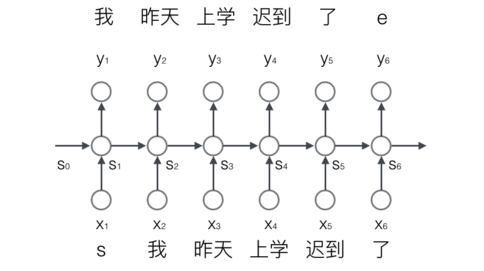
其中，s和e是两个特殊的词，分别表示一个序列的开始和结束。
整个计算过程下图所示，第一个单词被转换成机器可读的向量。然后，RNN 逐个处理向量序列

在处理过程中，它将之前的隐状态传递给序列的下一个步骤。隐状态作为神经网络的记忆，保存着网络先前观察到的数据信息。

13.2.5 .1向量化

神经网络的输入和输出都是向量，为了让语言模型能够被神经网络处理，我们必须把词表达为向量的形式，这样神经网络才能处理它。
神经网络的输入是词，我们可以用下面的步骤对输入进行向量化：
1）建立一个包含所有词的词典，每个词在词典里面有一个唯一的编号。
2）任意一个词都可以用一个N维的one-hot向量来表示（也可以采用word2vec方式）。其中，N是词典中包含的词的个数。假设一个词在词典中的编号是i，v是表示这个词的向量，是向量的第j个元素，则：

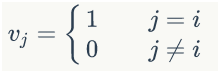
上面这个公式的含义，可以用下面的图来直观的表示：

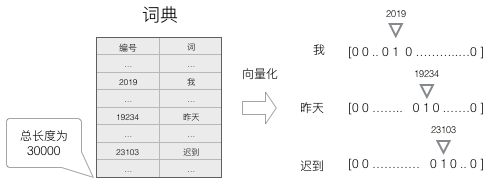
使用这种向量化方法，我们就得到了一个高维、稀疏的向量（稀疏是指绝大部分元素的值都是0）。处理这样的向量会导致我们的神经网络有很多的参数，带来庞大的计算量。因此，往往会需要使用一些降维方法，将高维的稀疏向量转变为低维的稠密向量。不过这个话题我们就不再这篇文章中讨论了。
语言模型要求的输出是下一个最可能的词，我们可以让循环神经网络计算计算词典中每个词是下一个词的概率，这样，概率最大的词就是下一个最可能的词。因此，神经网络的输出向量也是一个N维向量，向量中的每个元素对应着词典中相应的词是下一个词的概率。如下图所示：

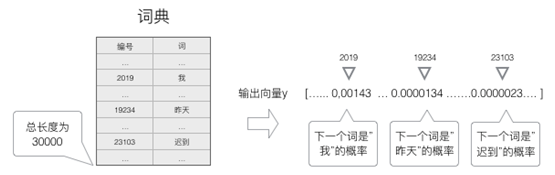
13.2.5 .2 Softmax层

前面提到，语言模型是对下一个词出现的概率进行建模。那么，怎样让神经网络输出概率呢？方法就是用softmax层作为神经网络的输出层。
我们先来看一下softmax函数的定义：

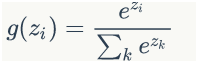
这个公式看起来有点抽象，我们举一个例子来说明。Softmax层如下图所示：

从上图我们可以看到，softmax layer的输入是一个向量，输出也是一个向量，两个向量的维度是一样的（在这个例子里面是4）。输入向量x=[1 2 3 4]经过softmax层之后，经过上面的softmax函数计算，转变为输出向量y=[0.03 0.09 0.24 0.64]。计算过程为：

我们来看看输出向量y的特征：
1）每一项为取值为0-1之间的正数；
2）所有项的总和是1。
我们不难发现，这些特征和概率的特征是一样的，因此我们可以把它们看做是概率。对于语言模型来说，我们可以认为模型预测下一个词是词典中第一个词的概率是0.03，是词典中第二个词的概率是0.09，以此类推。

13.2.5 .3语言模型的训练

可以使用监督学习的方法对语言模型进行训练，首先，需要准备训练数据集。接下来，我们介绍怎样把语料。

转换成语言模型的训练数据集。
首先，我们获取输入-标签对：

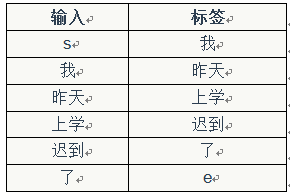
然后，使用前面介绍过的向量化方法，对输入x和标签y进行向量化。这里面有意思的是，对标签y进行向量化，其结果也是一个one-hot向量。例如，我们对标签『我』进行向量化，得到的向量中，只有第2019个元素的值是1，其他位置的元素的值都是0。它的含义就是下一个词是『我』的概率是1，是其它词的概率都是0。
最后，我们使用交叉熵误差函数作为优化目标，对模型进行优化。
在实际工程中，我们可以使用大量的语料来对模型进行训练，获取训练数据和训练的方法都是相同的。

13.2.5 .4交叉熵误差

一般来说，当神经网络的输出层是softmax层时，对应的误差函数E通常选择交叉熵误差函数，其定义如下：

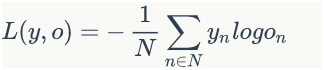
当然我们可以选择其他函数作为我们的误差函数，比如最小平方误差函数(MSE)。不过对概率进行建模时，选择交叉熵误差函数更合理一些。

13.3 LSTM网络

前面我们介绍了循环神经网络的简单模型，这种模型有很多不足，尤其是层数稍多时出现梯度消失或爆炸的情况。为解决这些问题，研究人员苦苦探究，经过近8年的不懈努力，终于结出硕果，于1997年由Sepp Hochreiter和Jürgen Schmidhuber首次提出LSTM(Long Short Term Memory Network, LSTM)，它成功的解决了原始循环神经网络的缺陷，成为当前最流行的RNN，在语音识别、图片描述、自然语言处理等许多领域中成功应用。2014年首次使用的GRU是LSTM的一个简单变体，它们拥有许多相同的属性。我们先看看LSTM，然后看看GRU是如何不同的。

13.3.1 LSTM网络

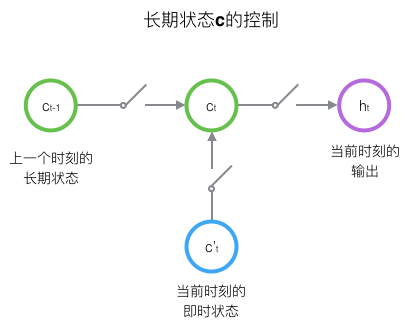
LSTM的思路比较简单。原始RNN的隐藏层只有一个状态，即h，它对于短期的输入非常敏感。那么，假如我们再增加一个状态，即c，让它来保存长期的状态，那么问题不就解决了么？如下图所示：

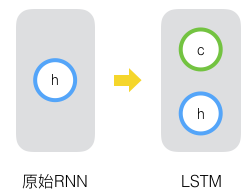
新增加的状态c，称为单元状态(cell state)。我们把上图按照时间维度展开：

LSTM的关键，就是怎样控制长期状态c。在这里，LSTM的思路是使用三个控制开关。第一个开关，负责控制继续保存长期状态c；第二个开关，负责控制把即时状态输入到长期状态c；第三个开关，负责控制是否把长期状态c作为当前的LSTM的输出。三个开关的作用如下图所示：

13.3.2 LSTM前向计算

前面描述的开关是怎样在算法中实现的呢？这就用到了门（gate）的概念。门实际上就是一层全连接层，它的输入是一个向量，输出是一个0到1之间的实数向量。假设W是门的权重向量，b是偏置项，那么门可以表示为：

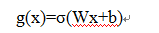
门的使用，就是用门的输出向量按元素乘以我们需要控制的那个向量。因为门的输出是0到1之间的实数向量，那么，当门输出为0时，任何向量与之相乘都会得到0向量，这就相当于啥都不能通过；输出为1时，任何向量与之相乘都不会有任何改变，这就相当于啥都可以通过。因为σ（也就是sigmoid函数）的值域是(0,1)，所以门的状态都是半开半闭的。
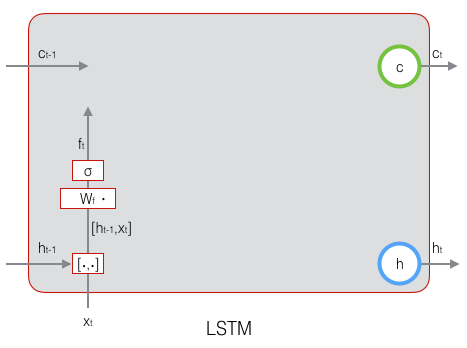
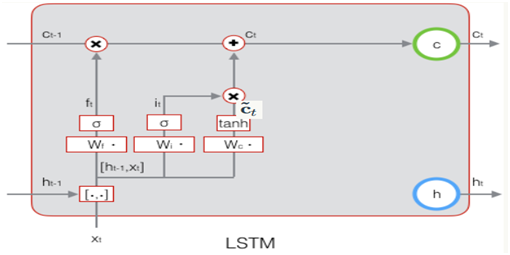
下图显示了遗忘门的计算过程：

 
下图为遗忘门的计算公式：

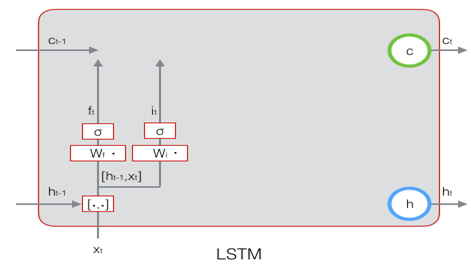
下图描述了输入门的计算过程：

下图演示了状态的计算过程:

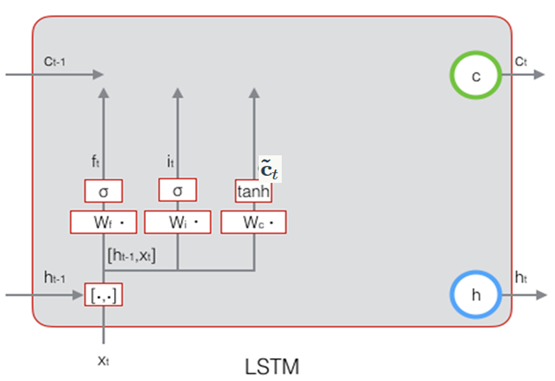
下图表示输出门的过程及计算公式:

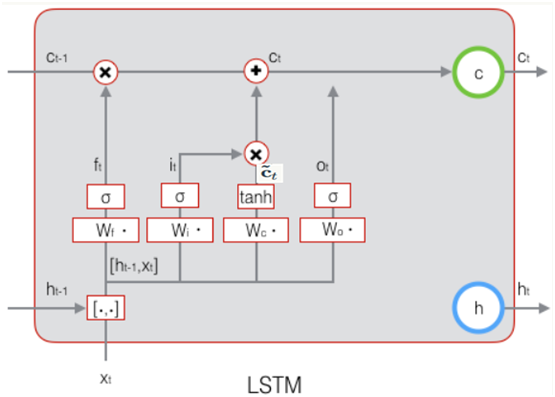
LSTM最终的输出，是由输出门和单元状态共同确定的：


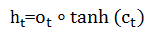
下图表示LSTM最终输出的计算:

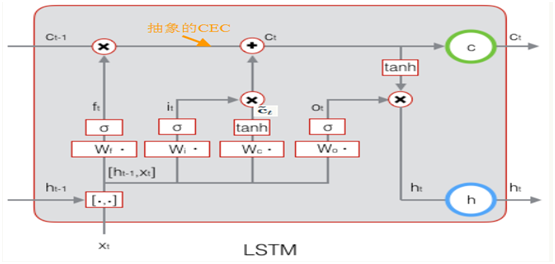
除了LSTM的四个门控制其状态外，LSTM还有一个固定权值为1的自连接，以及一个线性激活函数，因此，其局部偏导数始终为1。 在反向传播阶段，这个所谓的常量误差传输子（constant error carousel,CEC）能够在许多时间步中携带误差面不会发生梯度消失或梯度爆炸。

13.3.3 LSTM的训练

13.3.3.1 LSTM训练算法主要步骤

2）反向计算每个神经元的误差项值。与循环神经网络一样，LSTM误差项的反向传播也是包括两个方向：
一个是沿时间的反向传播，即从当前t时刻开始，计算每个时刻的误差项；
一个是将误差项向上一层传播。
3）根据相应的误差项，计算每个权重的梯度。
整个推导过程比较长，有兴趣的读者可参考这篇博文，这里只列出一些结果，过程就省略了。

13.3.3.2关于公式和符号的说明

为便于大家理解，预定义一些公式及运算符号等，这些公式或运算在推导一些结论时需要用到。

13.3.3.2误差项沿时间的反向传递

将误差项向前传递到任意k时刻的公式：

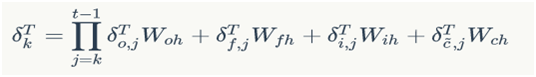
13.3.3.3将误差项传递到上一层

13.3.3.4权重梯度的计算

13.4 GRU网络

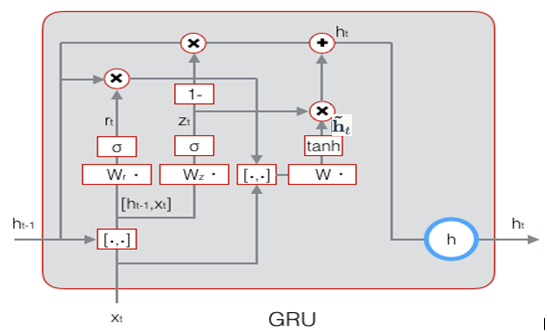
前面我们介绍了RNN的改进版LSTM，它有效克服了传统RNN的一些不足，事物总是向前发展的，LSTM也存在很多变体，在众多的LSTM变体中，GRU (Gated Recurrent Unit)也许是最成功的一种。它对LSTM做了很多简化，同时却保持着和LSTM相同的效果。因此，GRU最近变得越来越流行。
GRU对LSTM做了两个大改动：

GRU的前向计算公式为：

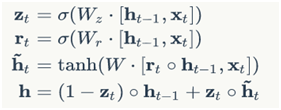
GRU的示意图：

13.5 Bi-LSTM网络

双向循环神经网络(Bidirectional Recurrent Neural Networks,Bi-RNN)，Schuster、Paliwal，1997年首次提出，和LSTM同年。Bi-RNN，增加RNN可利用信息。普通MLP，数据长度有限制。RNN，可以处理不固定长度时序数据，无法利用历史输入未来信息。Bi-RNN，同时使用时序数据输入历史及未来数据，时序相反两个循环神经网络连接同一输出，输出层可以同时获取历史未来信息。
Language Modeling，不适合Bi-RNN，目标是通过前文预测下一单词，不能将下文信息传给模型。不过对分类问题，手写文字识别、机器翻译、蛋白结构预测等，采用Bi-RNN能提升模型效果。百度语音识别，通过Bi-RNN综合上下文语境，提升模型准确率。
双向循环神经网络（BRNN）的基本思想是提出每一个训练序列向前和向后分别是两个循环神经网络（RNN），而且这两个都连接着一个输出层。这个结构提供给输出层输入序列中每一个点的完整的过去和未来的上下文信息。下图展示的是一个沿着时间展开的双向循环神经网络。六个独特的权值在每一个时步被重复的利用，六个权值分别对应：输入到向前和向后隐含层（w1, w3），隐含层到隐含层自己（w2, w5），向前和向后隐含层到输出层（w4, w6）。值得注意的是：向前和向后隐含层之间没有信息流，这保证了展开图是非循环的。

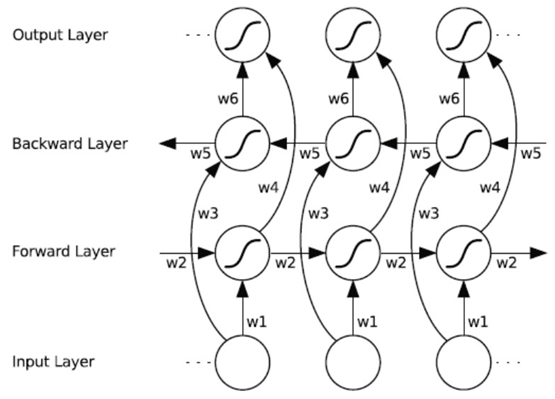
13.6 一些优化方法

选择rmsprop优化算法
rmsprop优化算法背后的基本思想是根据先前梯度的和来调整学习率per-parameter。直观的 ，它意味着频繁出现的特征得到更小的学习率（因为它的梯度的和将会更大），稀有的特征得到更大的学习率； rmsprop的实现相当的简单；对于每个参数，有一个缓存变量。 在梯度下降时，我们更新参数和此变量；
cacheW = decay * cacheW + (1 - decay) * dW ** 2
W = W - learning_rate * dW / np.sqrt(cacheW + 1e-6)
衰退典型的被设置为0.9或0.95，1e-6 是为了避免0的出现；
加入嵌入层
使用例如word2vect和GloVe单词嵌入是一个流行的方法提高我们精度。代替使用one-hot vector来表达单词，使用word2vec或GloVe学习得到的携带语义的低维向量（形似的单词具有相似的向量），使用这些向量是训练前预处理的一种方式，直观的，能够告诉神经网络那些单词是相似的，以至于需要更少的学习语言；在你没有大量数据的时候，使用预训练向量很有效，因为它允许神经网络推广到没有见过的单词。我没有使用过预处理单词向量，但是加入一个嵌入层使它们更容易的插入进来；嵌入矩阵（E）就是一个查找表。第i列向量对应于我们的单词表中的第i个单词；
通过更新E进行单词的向量表示的学习更新；但是，这与我们的特殊任务相关，并不是可以下载使用大量文档寻训练的模型进行通用；
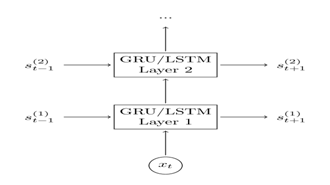
添加第二个GRU层
在神经网络中，加入第二层能够使我们的模型捕捉到更高水平相互作用；你能够加入额外的层；你将会发现在2-3层之后，结果会衰退，除非你拥有大量的数据，更多的层次不太可能造成大的差异，可能导致过拟合。

13.7 应用场景

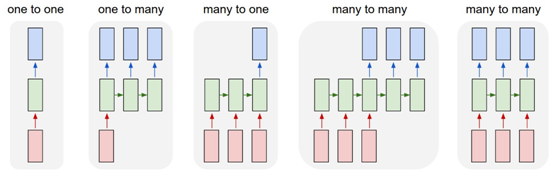
上图中每一个矩形是一个向量，箭头则表示函数（比如矩阵相乘）。输入向量用红色标出，输出向量用蓝色标出，绿色的矩形是RNN的状态。从做到右：
（1）没有使用RNN的Vanilla模型，从固定大小的输入得到固定大小输出（比如图像分类）。

（2）序列输出（比如图片字幕，输入一张图片输出一段文字序列）。
（3）序列输入（比如情感分析，输入一段文字然后将它分类成积极或者消极情感）。
（4）序列输入和序列输出（比如机器翻译：一个RNN读取一条英文语句然后将它以法语形式输出）。
（5）同步序列输入输出（比如视频分类，对视频中每一帧打标签）。
我们注意到在每一个案例中，都没有对序列长度进行预先特定约束，因为递归变换（绿色部分）是固定的，而且我们可以多次使用。
正如你预想的那样，与使用固定计算步骤的固定网络相比，使用序列进行操作要更加强大，因此，这激起了我们建立对智能系统更大的兴趣。而且，我们可以从一小方面看出，RNNs将输入向量与状态向量用一个固定（但可以学习）函数绑定起来，从而用来产生一个新的状态向量。在编程层面，在运行一个程序时，可以用特定的输入和一些内部变量对其进行解释。从这个角度来看，RNNs本质上可以描述程序。事实上， RNNs是图灵完备的 ，即它们可以模拟任意程序（使用恰当的权值向量）。
13.8 LSTM实例之一（Python3实现）
前面我们介绍了LSTM的主要框架及原理，以及多种LSTM的改进模型，接下来我们通过一个实例来说明LSTM的具体实现。使用python3，后续我们将使用Tensorflow、Keras等实现。在下面的实现中，LSTMLayer的参数包括输入维度、输出维度、隐藏层维度，单元状态维度等于隐藏层维度。gate的激活函数为sigmoid函数，输出的激活函数为tanh。

13.8.1 LSTM实激活函数的实现

我们当然可以选择其他函数作为我们的误差函数，比如最小平方误差函数(MSE)。不过对概率进行建模时，选择交叉熵误差函数更make sense。

13.8.2 LSTM初始化

我们把LSTM的实现放在LstmLayer类中，根据LSTM前向计算和反向传播算法，我们需要初始化一系列矩阵和向量。这些矩阵和向量有两类用途，
一类是用于保存模型参数，例如：

另一类是保存各种中间计算结果，以便于反向传播算法使用，它们包括：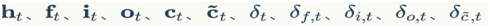

以及各个权重对应的梯度。
在构造函数的初始化中，只初始化了与forward计算相关的变量，与backward相关的变量没有初始化。

13.8.3前向计算的实现

forward方法实现了LSTM的前向计算：

从上面的代码我们可以看到，门的计算都是相同的算法，而门和c ̃_t的计算仅仅是激活函数不同。因此我们提出了calc_gate方法，这样减少了很多重复代码

13.8.4反向传播算法的实现

backward方法实现了LSTM的反向传播算法。需要注意的是，与backword相关的内部状态变量是在调用backward方法之后才初始化的。这种延迟初始化的一个好处是，如果LSTM只是用来推理，那么就不需要初始化这些变量，节省了很多内存。

算法主要分成两个部分，一部分使计算误差项：

另一部分是计算梯度：

13.8.5梯度下降算法的实现

下面是用梯度下降算法来更新权重

13.8.6梯度检查的实现

和RecurrentLayer一样，为了支持梯度检查，我们需要支持重置内部状态。

梯度检查的代码：

13.8.7 运行

为便于运行，需要把一些函数，如forward、calc_gate、backward、calc_gradient等整合到LstmLayer类中
具体如下：

运行检查梯度函数
gradient_check()
运行结果如下：

-----2-----
[[ 3.54293058e-10 9.68056914e-11]
[ 9.68010040e-11 2.64495392e-11]]
[[ 3.54293058e-10 9.68056914e-11]
[ 9.68010040e-11 2.64495392e-11]]
-----1-----
[[ 0. 0.]
[ 0. 0.]]
[[ 3.54293058e-10 9.68056914e-11]
[ 9.68010040e-11 2.64495392e-11]]
weights(0,0): expected - actural 3.5432e-10 - 3.5429e-10
weights(0,1): expected - actural 9.6844e-11 - 9.6806e-11
weights(1,0): expected - actural 9.6801e-11 - 9.6801e-11
weights(1,1): expected - actural 2.6420e-11 - 2.6450e-11

参考：https://zybuluo.com/hanbingtao/note/541458