NumPy是Python基础,更是数据科学的通用语言,而且与TensorFlow关系密切,所以我们把它列为第一章。
NumPy为何如此重要?实际上Python本身含有列表(list)和数组(array),但对于大数据来说,这些结构有很多不足。因列表的元素可以是任何对象,因此列表中所保存的是对象的指针。这样为了保存一个简单的[1,2,3],都需要有3个指针和三个整数对象。对于数值运算来说这种结构显然比较浪费内存和CPU计算时间。 至于array对象,它直接保存数值,和C语言的一维数组比较类似。但是由于它不支持多维,也没有各种运算函数,因此也不适合做数值运算。
NumPy(Numerical Python 的简称)的诞生弥补了这些不足,NumPy提供了两种基本的对象:ndarray(N-dimensional array object)和 ufunc(universal function object)。ndarray是存储单一数据类型的多维数组,而ufunc则是能够对数组进行处理的函数。
NumPy的主要特点:
ndarray,快速和节省空间的多维数组,提供数组化的算术运算和高级的广播功能。
使用标准数学函数对整个数组的数据进行快速运算,而不需要编写循环。
读取/写入磁盘上的阵列数据和操作存储器映像文件的工具。
线性代数,随机数生成,和傅里叶变换的能力。
集成C,C++,Fortran代码的工具。
在使用 NumPy 之前,需要先导入该模块:
|
1 |
import numpy as np |
本章主要内容如下:
如何生成NumPy的ndarray的几种方式
如何存取元素
如何操作矩阵
如何合并或拆分数据
简介NumPy的通用函数
简介NumPy的广播机制
1.1生成ndarray的几种方式
NumPy封装了一个新的数据类型ndarray(n-dimensional array),一个多维数组对象,该对象封装了许多常用的数学运算函数,方便我们做数据处理,以及数据分析,如何生成ndarray呢?这里我们介绍生成ndarray的几种方式,如从已有数据中创建;利用random创建;创建特殊多维数组;使用arange函数等。
1.从已有数据中创建
直接对python的基础数据类型(如列表、元组等)进行转换来生成ndarray。
(1)将列表变换成ndarray
|
1 2 3 4 5 |
import numpy as np list1 = [3.14,2.17,0,1,2] nd1 = np.array(list1) print(nd1) print(type(nd1)) |
打印结果
[ 3.14 2.17 0. 1. 2. ]
<class 'numpy.ndarray'>
(2)嵌套列表可以转换成多维ndarray
|
1 2 3 4 5 |
import numpy as np list2 = [[3.14,2.17,0,1,2],[1,2,3,4,5]] nd2 = np.array(list2) print(nd2) print(type(nd2)) |
打印结果
[[ 3.14 2.17 0. 1. 2. ]
[ 1. 2. 3. 4. 5. ]]
<class 'numpy.ndarray'>
如果把(1)和(2)中的列表换成元组也同样适合。
2.利用random模块生成ndarray
在深度学习中,我们经常需要对一些变量进行初始化,适当的初始化能提高模型的性能。通常我们用随机数生成模块random来生成,当然random模块又分为多种函数:
random生成0到1之间的随机数;uniform生成均匀分布随机数;randn生成标准正态的随机数;normal生成正态分布;shuffle随机打乱顺序;seed设置随机数种子等等,以下我们列举几个简单示例。
|
1 2 3 4 5 |
import numpy as np nd5 = np.random.random([3,3]) print(nd5) print(type(nd5)) |
打印结果
[[ 0.88900951 0.47818541 0.91813526]
[ 0.48329167 0.63730656 0.14301479]
[ 0.9843789 0.99257093 0.24003961]]
<class 'numpy.ndarray'>
生成一个随机种子,对生成的随机数打乱。
|
1 2 3 4 5 6 7 8 9 |
import numpy as np np.random.seed(123) nd5_1 = np.random.randn(2,3) print(nd5_1) np.random.shuffle(nd5_1) print("随机打乱后数据") print(nd5_1) print(type(nd5_1)) |
打印结果
[[-1.0856306 0.99734545 0.2829785 ]
[-1.50629471 -0.57860025 1.65143654]]
随机打乱后数据
[[-1.50629471 -0.57860025 1.65143654]
[-1.0856306 0.99734545 0.2829785 ]]
<class 'numpy.ndarray'>
3. 创建特定形状的多维数组
数据初始化时,有时需要生成一些特殊矩阵,如0或1的数组或矩阵,这时我们可以利用np.zeros,np.ones,np.diag来实现,以下我们通过几个示例来说明。
|
1 2 3 4 5 6 7 8 9 10 |
import numpy as np #生成全是0的3x3矩阵 nd6 = np.zeros([3,3]) #生成全是1的3x3矩阵 nd7 = np.ones([3,3]) #生成3阶的单位矩阵 nd8= np.eye(3) #生成3阶对角矩阵 print (np.diag([1, 2, 3])) |
我们还可以把生成的数据保存到磁盘,然后从磁盘读取。
|
1 2 3 4 |
import numpy as np nd9 = np.random.random([5,5]) np.savetxt(X=nd9,fname='./test2.txt') nd10 = np.loadtxt('./test2.txt') |
4.利用arange函数
arange是numpy模块中的函数,其格式为:arange([start,] stop[, step,], dtype=None)
根据start与stop指定的范围,以及step设定的步长,生成一个 ndarray,其中start缺省值为0,步长step可为小数。
|
1 2 3 4 5 6 |
import numpy as np print(np.arange(10)) print(np.arange(0,10)) print(np.arange(1, 4,0.5)) print(np.arange(9, -1, -1)) |
1.2存取元素
上节我们介绍了生成ndarray的几种方法,数据生成后,如何读取我们需要的数据?这节我们介绍几种读取数据的方法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np np.random.seed(2018) nd11 = np.random.random([10]) #获取指定位置的数据,获取第4个元素 nd11[3] #截取一段数据 nd11[3:6] #截取固定间隔数据 nd11[1:6:2] #倒序取数 nd11[::-2] #截取一个多维数组的一个区域内数据 nd12=np.arange(25).reshape([5,5]) nd12[1:3,1:3] #截取一个多维数组中,数值在一个值域之内的数据 nd12[(nd12>3)&(nd12<10)] #截取多维数组中,指定的行,如读取第2,3行 nd12[[1,2]] #或nd12[1:3,:] ##截取多维数组中,指定的列,如读取第2,3列 nd12[:,1:3] |
如果你对上面这些获取方式还不是很清楚,没关系,下面我们通过图形的方式说明如何获取多维数组中的元素,如图1-1所示,左边的为表达式,右边为对应获取元素。
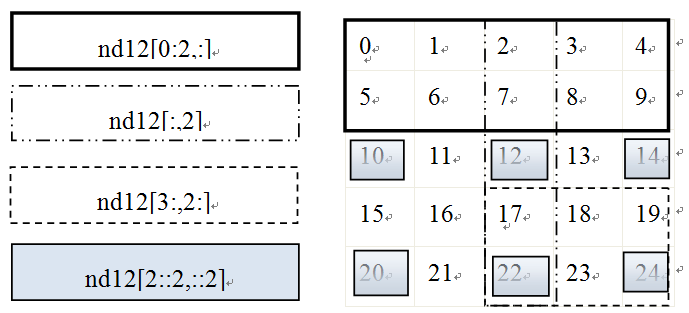
图1-1 获取多维数组中的元素
获取数组中的部分元素除通过指定索引标签外,还可以使用一些函数来实现,如通过random.choice函数可以从指定的样本中进行随机抽取数据。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np from numpy import random as nr a=np.arange(1,25,dtype=float) c1=nr.choice(a,size=(3,4)) #size指定输出数组形状 c2=nr.choice(a,size=(3,4),replace=False) #replace缺省为True,即可重复抽取。 #下式中参数p指定每个元素对应的抽取概率,缺省为每个元素被抽取的概率相同。 c3=nr.choice(a,size=(3,4),p=a / np.sum(a)) print("随机可重复抽取") print(c1) print("随机但不重复抽取") print(c2) print("随机但按制度概率抽取") print(c3) |
打印结果:
随机可重复抽取
[[ 7. 22. 19. 21.]
[ 7. 5. 5. 5.]
[ 7. 9. 22. 12.]]
随机但不重复抽取
[[ 21. 9. 15. 4.]
[ 23. 2. 3. 7.]
[ 13. 5. 6. 1.]]
随机但按制度概率抽取
[[ 15. 19. 24. 8.]
[ 5. 22. 5. 14.]
[ 3. 22. 13. 17.]]
1.3矩阵操作
深度学习中经常涉及多维数组或矩阵的运算,正好NumPy模块提供了许多相关的计算方法,下面介绍一些常用的方法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import numpy as np nd14=np.arange(9).reshape([3,3]) #矩阵转置 np.transpose(nd14) #矩阵乘法运算 a=np.arange(12).reshape([3,4]) b=np.arange(8).reshape([4,2]) a.dot(b) #求矩阵的迹 a.trace() #计算矩阵行列式 np.linalg.det(nd14) #计算逆矩阵 c=np.random.random([3,3]) np.linalg.solve(c,np.eye(3)) |
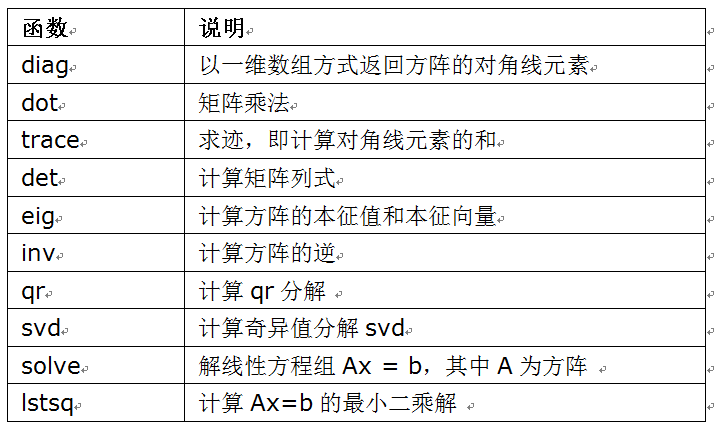
上面介绍的几种方法是numpy.linalg模块中的函数,numpy.linalg模块中的函数是满足行业标准级的Fortran库,具体请看表1-1。
表1-1 numpy.linalg中常用函数
1.4数据合并与展平
在机器学习或深度学习中,经常遇到需要把多个向量或矩阵按某轴方向进行合并,展平也经常使用,如在卷积或循环神经网络中,在全连接层之前,需要把矩阵展平。这节介绍几种数据合并和展平的方法。
(1)合并一维数组
|
1 2 3 4 5 6 7 8 |
import numpy as np a=np.array([1,2,3]) b=np.array([4,5,6]) c=np.append(a,b) print(c) #或利用concatenate d=np.concatenate([a,b]) print(d) |
打印结果:
[1 2 3 4 5 6]
[1 2 3 4 5 6]
(2)多维数组的合并
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import numpy as np a=np.arange(4).reshape(2,2) b=np.arange(4).reshape(2,2) #按行合并 c=np.append(a,b,axis=0) print(c) print("合并后数据维度",c.shape) #按列合并 d=np.append(a,b,axis=1) print("按列合并结果:") print(d) print("合并后数据维度",d.shape) |
打印结果
[[0 1]
[2 3]
[0 1]
[2 3]]
合并后数据维度 (4, 2)
按列合并结果:
[[0 1 0 1]
[2 3 2 3]]
合并后数据维度 (2, 4)
(3)矩阵展平
|
1 2 3 4 5 6 7 8 9 |
import numpy as np nd15=np.arange(6).reshape(2,-1) print(nd15) #按照列优先,展平。 print("按列优先,展平") print(nd15.ravel('F')) #按照行优先,展平。 print("按行优先,展平") print(nd15.ravel()) |
打印结果
[[0 1 2]
[3 4 5]]
按列优先,展平
[0 3 1 4 2 5]
按行优先,展平
[0 1 2 3 4 5]
1.5通用函数
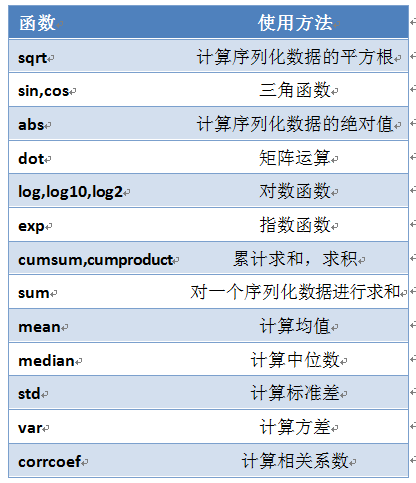
NumPy提供了两种基本的对象,即ndarray和ufunc对象。前面我们对ndarray作了简单介绍,本节将介绍它的另一个对象ufunc,ufunc(通用函数)是universal function的缩写,它是一种能对数组的每个元素进行操作的函数。许多ufunc函数都是在c语言级别实现的,因此它们的计算速度非常快。此外,功能比math模块中函数更灵活。math模块的输入一般是标量,但NumPy中函数可以是向量或矩阵,而利用向量或矩阵可以避免循环语句,这点在机器学习、深度学习中经常使用。表1-2为NumPy常用几个通用函数。
表1-2 NumPy几个常用通用函数
(1)使用math与numpy函数性能比较:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import time import math import numpy as np x = [i * 0.001 for i in np.arange(1000000)] start = time.clock() for i, t in enumerate(x): x[i] = math.sin(t) print ("math.sin:", time.clock() - start ) x = [i * 0.001 for i in np.arange(1000000)] x = np.array(x) start = time.clock() np.sin(x) print ("numpy.sin:", time.clock() - start ) |
打印结果
math.sin: 0.5169950000000005
numpy.sin: 0.05381199999999886
由此可见,numpy.sin比math.sin快近10倍。
(2)使用循环与向量运算比较:
充分使用python的numpy库中的内建函数(built-in function),实现计算的向量化,可大大提高运行速度。Python的NumPy库中的内建函数使用了SIMD指令。例如下面所示在Python中使用向量化要比使用循环计算速度快得多。如果使用GPU,其性能将更强大,不过NumPy不提供GPU支持。TensorFlow提供GPU,第8章将介绍TensorFlow如何使用GPU来加速算法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import time import numpy as np x1 = np.random.rand(1000000) x2 = np.random.rand(1000000) ##使用循环计算向量点积 tic = time.process_time() dot = 0 for i in range(len(x1)): dot+= x1[i]*x2[i] toc = time.process_time() print ("dot = " + str(dot) + "\n for loop----- Computation time = " + str(1000*(toc - tic)) + "ms") ##使用numpy函数求点积 tic = time.process_time() dot = 0 dot = np.dot(x1,x2) toc = time.process_time() print ("dot = " + str(dot) + "\n verctor version---- Computation time = " + str(1000*(toc - tic)) + "ms") |
打印结果
dot = 250215.601995
for loop----- Computation time = 798.3389819999998ms
dot = 250215.601995
verctor version---- Computation time = 1.885051999999554ms
从程序运行结果上来看,该例子使用for循环运行时间是使用向量运算运行时间的约400倍。因此,深度学习算法中,一般都使用向量化矩阵运算。
1.6 广播机制
广播机制(Broadcasting)的功能是为了方便不同shape的array(numpy库的核心数据结构)进行数学运算。广播提供了一种向量化数组操作的方法,以便在C中而不是在Python中进行循环,这通常会带来更高效的算法实现。广播的兼容原则为:
(1)对齐尾部维度
(2)shape相等or其中shape元素中有一个为1
以下通过实例来具体说明。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import numpy as np a=np.arange(10) b=np.arange(10) #两个shape相同的数组相加 print(a+b) #一个数组与标量相加 print(a+3) #两个向量相乘 print(a*b) #多维数组之间的运算 c=np.arange(10).reshape([5,2]) d=np.arange(2).reshape([1,2]) #首先将d数组进行复制扩充为[5,2],如何复制请参考图1-2,然后相加。 print(c+d) |
打印结果
[ 0 2 4 6 8 10 12 14 16 18]
[ 3 4 5 6 7 8 9 10 11 12]
[ 0 1 4 9 16 25 36 49 64 81]
[[ 0 2]
[ 2 4]
[ 4 6]
[ 6 8]
[ 8 10]]
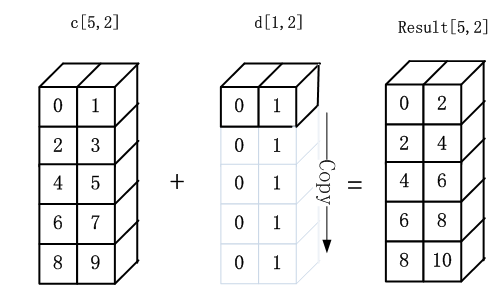
图1-2 NumPy多维数组相加
有时为了保证矩阵运算正确,我们可以使用reshape()函数来变更矩阵的维度。
1.7小结
本章简单介绍了NumPy模块的两个基本对象ndarray、ufunc,介绍了ndarray对象的几种生成方法,及如何存取其元素、如何操作矩阵或多维数组、如何进行数据合并与展平等。最后说明了通用函数及广播机制。如果想进一步了解NumPy,大家可参考:http://www.numpy.org/
Pingback引用通告: Python深度学习—-TensorFlow卷 – 飞谷云人工智能