26.1交通标志识别简介
26.1.1 交通标记易识特性
由于交通标志采用特定的文字、图形和符号,在一定范围内具有标准、醒目、信息明确的特性,一直是图像识别技术在交通领域应用的首选。从图像识别技术诞生之日起,交通标志识别的算法和模型就一直受到广泛的关注,也让这一技术发展相对成熟,并应用到自动驾驶领域中来。

图1 交通标志识别技术
我国的交通标志一共有一百余种,按类别可分为黄底黑边的警告标志、白底红圈的禁令标志、蓝底白字的指示标志,形状上以三角形、圆形和矩形为主。明确的形状和颜色区分、有限的标志数量,都为图像识别提供了一个相对稳定的应用环境。
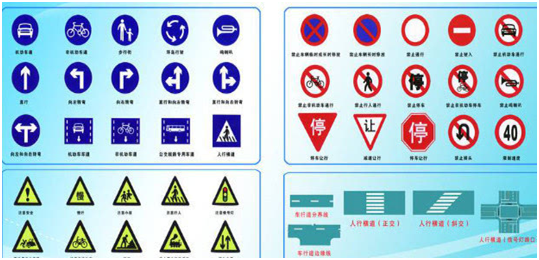
图2 我国的交通标志
26.1.2交通标志识别技术的原理
利用图像识别技术的交通标志识别系统一般分为以下几个工作步骤:
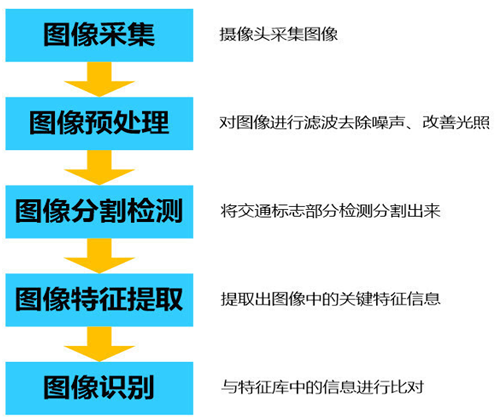
图3 图像识别的步骤
1. 图像预处理:
在实际的交通场景中,由于运动抖动、自然光、天气条件等各种因素的影响,不可避免的会在采集的图像中引入一定程度的干扰和噪声,所以首先需要将这些不利因素消除,对采集到的图像进行一些预处理。通过图像均衡、图像增强和图像去噪等算法,将图像的光线均衡,突出关键信息。这一步基本和美图秀秀中的那些工具类似,都是将图像变得清晰、易辨认。

图4 对图像进行预处理,去除噪声、提高亮度和对比度
2. 交通标志分割:
预处理后的图像仍然包含很多信息,交通标志在其中只有很小的一个区域,为了减小处理的数据量,加快处理速度,一般都会先将交通标志的区域检测出来,再去判断这个区域中的交通标志的具体含义。交通标志在颜色和形状上都有一定的特殊性,并可按照下图进行一定程度的分类,所以一般通过这两个特征去检测交通标志。
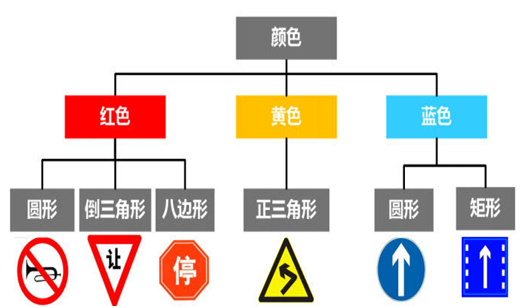
图5 交通标志按颜色和形状分类
2.1颜色分割:
颜色按照国际标准可划分为RGB、HSV、HSI等颜色空间,并进行量化分析,以RGB空间为例,将颜色按照红色、绿色、蓝色三种颜色进行分割,通过给定交通标志牌中常用的蓝色、黄色、红色的色度坐标范围,即可过滤掉与之不相关的颜色信息,快速检测到交通标志牌。

图 6 通过RGB色彩空间处理,快速定位红色区域
2.2形状分割:
仅仅检测颜色显然又是不够的,由于光照、背景色的影响和干扰,还需要在颜色检测结果的基础上对相应区域进行形状检测。交通标志具有边缘清晰、形状简单易辨认的特点。这些特征在排除颜色影响后的灰度图像中更加明显,因此通过一定的边缘检测算子去判断图像像素中出现的灰度阶跃变化,一般就能较为准确的检测出交通标志的形状和轮廓特征。

图7 对检测区域进行灰度处理,再通过灰度阶跃检测其形状边界
3. 交通标志特征提取
在图像检测完成以后,图像中基本就只剩下了交通标志的关键信息,这些信息简单直观,但计算机依然不会知道这些信息的具体含义,这时候需要再进一步对这些图像特征进行提取和比对,才能对具体的信息进行识别。
图像的关键特征,是识别具体信息的关键因素,特征的好坏直接决定了识别的准确度。一般说来这些关键特征需要具有可区分性、简约性和抗干扰等几个要素,可区分性即不同标志的特征要具有足够的差异性,简约性是在保证可区分性的前提下用尽量少的数据表示图像特征,这可以保证检测的速度和效率,抗干扰度即图像特征信息要保证尽量少的会被噪声、自然光和图像畸变影响。
在交通标志识别上,一般会提取颜色特征、线条变化特征、矩特征、灰度直方图统计特征等等,并会在事先维护一个足够样本数量的特征库,包含现有交通标志的图像特征信息。在识别的时候将采集到的图像的特征提取出来与数据库中的条件进行比对,即可判断出该交通标志的实际意义。
4. 识别结果匹配
目前有多种方法实现图像特征与特征库数据的比对,最为简单直接的方式是模板匹配:即在特征库中将不同交通标志的特征参数规定为某些特定的参数,当所采集图像的特征参数在某个范围内,就判断是这个交通标志信息。但由于图像在采集的时候难免发生形状畸变、颜色失真等误差,在实际使用场景中用模板匹配来识别的成功率和准确度并不是特别高,即便优化了图像处理算法,也还有很多局限。

图 8 通过匹配特征库信息识别标志
近些年机器学习技术的发展,让图像识别也有了很大的变化,通过设定一些简单的判断条件,并在特征库中加入各种形态和场景下的学习样本,让系统不断加深交通标志识别的认知和识别概率。机器学习让识别不再依靠具体固定的参数,而是通过一系列的条件判断让系统找到概率最大的目标,以此提升识别的准确度和灵活性。这一技术在目前成为研究的热点,并有效提高了图像识别的准确率。
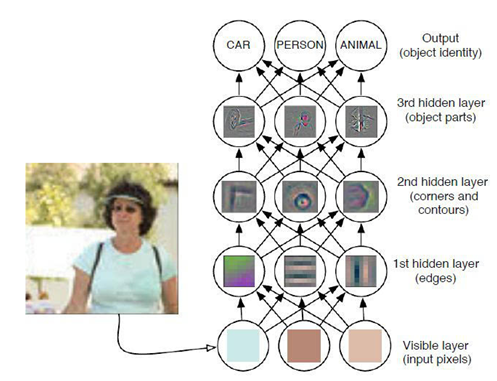
图 9 机器学习在图像识别中的应用
26.1.3 总结
交通标志识别是图像识别技术在自动驾驶领域较为成功的应用,其情景相对简单固定,识别准确度和成功率都让人满意。现在自动驾驶中摄像头识别车辆、行人、自行车、车道线等其他目标的工作原理基本和交通标志识别类似,只是针对不同的对象所用的的算法和模型也会进行一定的调整和优化,并维护一个更为多样的样本学习库。Mobileye在自动驾驶摄像头领域已经耕耘了17年,其算法集成优化、样本库丰富度、识别精确度都处于绝对领先,也为自动驾驶的普及带来了巨大的福音。
26.2 交通标志识别常用模型
1、LeNet(X)
是交通标志识别中非常经典的算法结构,其结构如下:
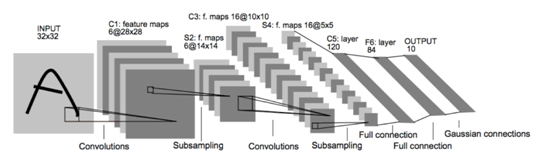
但是要实现交通标志识别还需要对该算法的初始结构进行调整。比如输出层的分类数调整为43;Subsampling layers 转为max pooling layers;增加Dropout 层,初始设置keep_prob=0.9;激活函数采用RELU。
改进后的架构流程如下表所示:

2、AlexNet
AlexNet是2012年发表的一个经典网络,在当年取得了ImageNet的最好成绩。
这是AlexNet的网络结构图:
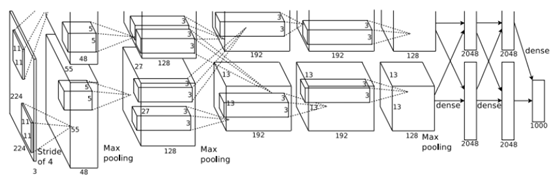
网络共有8层,其中前5层是卷积层,后边3层是全连接层,在每一个卷积层中包含了激励函数RELU以及局部响应归一化(LRN)处理,然后再经过池化(max pooling),最后的一个全连接层的输出是具有1000个输出的softmax层,最后的优化目标是最大化平均的多元逻辑回归。
3、其它多层神经网络
36.3 实例1(使用多层神经网络)
这个Project的目的是利用神经卷积网路(CNN)来分类(classify)常见的交通标志。 CNN 在读图领域已经全面超过了传统的机器学习方法(SVC, OpenCV)。大量的资料是深度学习准确性的保证, 在资料不够的情况下也可以人为的对原有资料进行小改动从而来提高识别的准确度。汇入必要的软体包(pickle, numpy, cv2, matplotlib, sklearn, tensorflow, Keras)
这里使用python3.6,TensorFlow1.6 等,使用GPU比使用CPU快约100倍!
1)导入需要的模块或库
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import pickle import cv2 import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import train_test_split from tensorflow.python.keras.preprocessing.image import ImageDataGenerator from sklearn.model_selection import train_test_split import tensorflow as tf from tensorflow.contrib.layers import flatten ### Load the images and plot them here. import os # Visualizations will be shown in the notebook. %matplotlib inline |
【注意】如果环境已安装keras,可以直接使用,导入方式可改为:
|
1 2 |
import pickle from keras.preprocessing.image import ImageDataGenerator |
资料来源: 和大部分的机器学习的要求一样, CNN需要大量有label的资料,German Traffic Sign Dataset提供了对于这个project的研究所需的数据,本章数据集下载
2)导入数据
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
training_file = '/home/wumg/data/autocar/train.p' # change it to your local dir testing_file = '/home/wumg/data/autocar/test.p' # change it to your local dir with open(training_file, mode='rb') as f: train = pickle.load(f) with open(testing_file, mode='rb') as f: test = pickle.load(f) X_train, y_train = train['features'], train['labels'] X_test, y_test = test['features'], test['labels'] # Number of training examples n_train = X_train.shape[0] # Number of testing examples. n_test = X_test.shape[0] # What's the shape of an traffic sign image? image_shape = X_train[0].shape # How many unique classes/labels there are in the dataset? n_classes = len(set(y_train)) print("Number of training examples =", n_train) print("Number of testing examples =", n_test) print("Image data shape =", image_shape) print("Number of classes =", n_classes) |
打印结果
Number of training examples = 39209
Number of testing examples = 12630
Image data shape = (32, 32, 3)
Number of classes = 43
3)探索数据
从上面我们可以看到有39209个用作训练的影象 和 12630个testing data。 39209张照片对于训练CNN来说是不够的(100000张以上是比较理想的资料量), 所以之后要加入data augment 的模组来人为增加资料。每张影象的大小是是32×32 并且有3个通道。总共有43个不同的label。我们也可以把每个label对应的图片随机选择一张画出来。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# show a random sample from each class of the traffic sign dataset rows, cols = 4, 12 fig, ax_array = plt.subplots(rows, cols) # ax_array is a array object consistint of plt object plt.suptitle('RANDOM SAMPLES FROM TRAINING SET (one for each class)') for class_idx, ax in enumerate(ax_array.ravel()): if class_idx < n_classes: cur_X = X_train[y_train == class_idx] cur_img = cur_X[np.random.randint(len(cur_X))] ax.imshow(cur_img) ax.set_title('{:02d}'.format(class_idx)) else: ax.axis('off') # hide both x and y ticks plt.setp([a.get_xticklabels() for a in ax_array.ravel()], visible=False) plt.setp([a.get_yticklabels() for a in ax_array.ravel()], visible=False) plt.draw() |

4)查看各种标志的分布情况
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
train_distribution, test_distribution = np.zeros(n_classes), np.zeros(n_classes) for c in range(n_classes): train_distribution[c] = np.sum(y_train == c) / n_train test_distribution[c] = np.sum(y_test == c) / n_test fig, ax = plt.subplots() col_width = 0.5 bar_train = ax.bar(np.arange(n_classes), train_distribution, width=col_width, color='r') bar_test = ax.bar(np.arange(n_classes)+col_width, test_distribution, width=col_width, color='b') ax.set_ylabel('PERCENTAGE OF PRESENCE') ax.set_xlabel('CLASS LABEL') ax.set_title('Classes distribution in traffic-sign dataset') ax.set_xticks(np.arange(0, n_classes, 5) ) ax.set_xticklabels(['{:02d}'.format(c) for c in range(0, n_classes, 5)]) ax.legend((bar_train[0], bar_test[0]), ('train set', 'test set')) plt.show() |

从上图可以看到这43个类别的资料量的分配是很不均匀的。这个会给CNN带来bias(偏见):CNN会更倾向于预测在training data里出现频率多的那些分类。
5)数据预处理
资料前期处理 根据这篇论文[Sermanet, LeCun], 把RGB的照片转化成YUV(除了RGB模型外,还有一种广泛采用的模型,称为YUV模型,又被称为亮度-色度模型(Luma-ChromaModel)。它是通过数学转换,将RGB三通道转换为一个代表亮度的通道(Y,又称为Luma),和两个代表色度的通道(UV,并称为Chroma)来记录图像的模型) 然后只选择Y通道的图片可以在不影响精度的同时减少资料计算量。然后每张图片都转化成以0为平均值, 以1为标准差的阵列。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
def preprocess_features(X, equalize_hist=True): # Convert from RGB to YUV X = np.array([np.expand_dims(cv2.cvtColor(rgb_img, cv2.COLOR_RGB2YUV)[:, :, 0], 2) for rgb_img in X]) # adjust image contrast if equalize_hist: X = np.array([np.expand_dims(cv2.equalizeHist(img), 2) for img in X]) X = np.float32(X) # Standardize features X -= np.mean(X, axis=0) X /= (np.std(X, axis=0) + np.finfo('float32').eps) return X X_train_norm = preprocess_features(X_train) X_test_norm = preprocess_features(X_test) |
人为添加数据(data augment) 对于图片来时, 一定程度的旋转, 上下左右移动, 放大或者缩小都应该不会影响它的标签。 虽然图片数据已经完全不一样了, 我们肉眼还是能够识别的出来, 这能够在增加数据量的同时帮助CNN 总结(generalize). Keras 有个很方便的函数ImageDataGenerator(rotation_range=15., zoom_range=0.2, width_shift_range=0.1, height_shift_range=0.1) 可以实现这个, 这个函数可以设置 旋转的角度rotation_range, 放大或缩小的倍数zoom_range, 左右移动的比例width_shift_range 和上下移动的比例height_shift_range , 随机在区间内改动原来的照片并产生无数新的照片, 下面我选择一张作为示范:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# creat the generator to perform online data augmentation image_datagen = ImageDataGenerator(rotation_range=15., zoom_range=0.2, width_shift_range=0.1, height_shift_range=0.1) # take a random image from the training set img_rgb = X_train[10] #print("img_rgb shape:",img_rgb.shape) # plot the original image plt.figure(figsize=(1,1)) plt.imshow(img_rgb) plt.title('Example of RGB image (class = {})'.format(y_train[10])) plt.axis('off') plt.show() # plot some randomly augmented images rows, cols = 4, 10 fig, ax_array = plt.subplots(rows, cols) for ax in ax_array.ravel(): augmented_img, _ = image_datagen.flow(np.expand_dims(img_rgb, 0), y_train[10:11]).next() ax.imshow(np.uint8(np.squeeze(augmented_img))) plt.setp([a.get_xticklabels() for a in ax_array.ravel()], visible=False) plt.setp([a.get_yticklabels() for a in ax_array.ravel()], visible=False) plt.suptitle('Random examples of data augment (starting from the previous image)') plt.show() |


6)搭建神经网络
搭建CNN 每一层的神经网络都加了dropout 来防止overfitting。这个CNN的特点是把两层conv的output做了一个合成:fc0 = tf.concat([flatten(drop1), flatten(drop2)],1 ) 然后再连接到fully_connected layer 和output layer(43 classes)。文献中说这样做的好处是“the classifier is explicitly provided both the local “motifs” (learned by conv1) and the more “global” shapes and structure (learned by conv2) found in the features.” 我的理解是: CNN 能够在图片的局部和整体都能作为判断的依据,从而提高准确率
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
n_classes = 43 def weight_variable(shape, mu=0, sigma=0.1): initialization = tf.truncated_normal(shape=shape, mean=mu, stddev=sigma) return tf.Variable(initialization) def bias_variable(shape, start_val=0.1): initialization = tf.constant(start_val,shape=shape) return tf.Variable(initialization) def conv2d(x, W, strides=[1,1,1,1], padding='SAME'): return tf.nn.conv2d(input=x, filter=W, strides=strides, padding=padding) def max_pool2x2(x): return tf.nn.max_pool(value=x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME') # network architecture definition def my_net(x, n_classes): c1_out = 64 conv1_W = weight_variable(shape=(3,3,1,c1_out)) #conv1_W = weight_variable(shape=(3,3,3,c1_out)) conv1_b = bias_variable(shape=(c1_out,)) conv1 = tf.nn.relu(conv2d(x, conv1_W) + conv1_b) pool1 = max_pool2x2(conv1) drop1 = tf.nn.dropout(pool1, keep_prob=keep_prob) c2_out = 128 conv2_W = weight_variable(shape=(3,3,c1_out, c2_out)) conv2_b = bias_variable(shape=(c2_out,)) conv2 = tf.nn.relu(conv2d(drop1, conv2_W) + conv2_b) pool2 = max_pool2x2(conv2) drop2 = tf.nn.dropout(pool2, keep_prob=keep_prob) fc0 = tf.concat([flatten(drop1), flatten(drop2)],1 ) fc1_out = 64 fc1_W = weight_variable(shape=(fc0.shape[1].value, fc1_out)) fc1_b = bias_variable(shape=(fc1_out,)) fc1 = tf.matmul(fc0, fc1_W) + fc1_b drop_fc1 = tf.nn.dropout(fc1, keep_prob=keep_prob) fc2_out = n_classes fc2_W = weight_variable(shape=(drop_fc1.shape[1].value, fc2_out)) fc2_b = bias_variable(shape=(fc2_out,)) logits = tf.matmul(drop_fc1, fc2_W) + fc2_b return logits tf.reset_default_graph() # placeholders x = tf.placeholder(dtype=tf.float32, shape=(None, 32, 32,1)) #x = tf.placeholder(dtype=tf.float32, shape=(None, 32, 32,3)) y = tf.placeholder(dtype=tf.int64, shape=None) keep_prob = tf.placeholder(tf.float32) # training pipeline lr = 0.0008 logits = my_net(x, n_classes=n_classes) cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=logits, labels=y) loss_function = tf.reduce_mean(cross_entropy) optimizer = tf.train.AdamOptimizer(learning_rate=lr) training_operation = optimizer.minimize(loss=loss_function) correct_prediction = tf.equal(tf.argmax(logits, 1), y) accuracy_operation = tf.reduce_mean(tf.cast(correct_prediction, tf.float32)) saver = tf.train.Saver() def evaluate(X_data, y_data): num_examples = len(X_data) total_accuracy = 0 sess = tf.get_default_session() for offset in range(0, num_examples, BATCH_SIZE): batch_x, batch_y = X_data[offset:offset+BATCH_SIZE], y_data[offset:offset+BATCH_SIZE] accuracy = sess.run(accuracy_operation, feed_dict={x: batch_x, y: batch_y, keep_prob:1.0}) total_accuracy += (accuracy * len(batch_x)) return total_accuracy / num_examples |
【备注】如果lr大小,如小于0.0001可能需要花费更多训练时间,如果太大,如0.1可能很难提高精度,所以选择合适lr很重要。
定义超参数
|
1 2 3 |
EPOCHS = 100 BATCHES_PER_EPOCH = 40 BATCH_SIZE = 128 |
【备注】大家可以根据情况,增加迭代次数,批量大小,批量一般不宜过大,否则将迅速增加训练时间。
7)训练CNN模型
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
with tf.Session() as sess: sess.run(tf.global_variables_initializer()) print("Training...") print() for epoch in range(EPOCHS): batch_counter = 0 for batch_x, batch_y in image_datagen.flow(X_train_norm, y_train, batch_size=BATCH_SIZE): batch_counter += 1 sess.run(training_operation, feed_dict={x: batch_x, y: batch_y, keep_prob:0.9}) if batch_counter == BATCHES_PER_EPOCH: break # at epoch end, evaluate accuracy on both training and validation set train_accuracy = evaluate(X_train_norm, y_train) #validation_accuracy = evaluate(X_validation, y_validation) print("EPOCH {} ...".format(epoch+1)) #print("Training Accuracy = {:.3f}, Validation Accuracy = {:.3f}".format(train_accuracy, validation_accuracy)) print("Training Accuracy = {:.3f}".format(train_accuracy)) print() saver.save(sess, save_path='./checkpoints/traffic_sign_model.ckpt', global_step=epoch) |
【备注】keep_prob参数控制dropout的比例,这个参数很重要,大家可以修改该参数,看它对精度的影响。
Training...
EPOCH 1 ...
Training Accuracy = 0.224
EPOCH 2 ...
Training Accuracy = 0.339
EPOCH 3 ...
Training Accuracy = 0.400
EPOCH 4 ...
Training Accuracy = 0.452
EPOCH 5 ...
Training Accuracy = 0.508
EPOCH 6 ...
Training Accuracy = 0.548
EPOCH 7 ...
Training Accuracy = 0.587
EPOCH 8 ...
Training Accuracy = 0.609
EPOCH 9 ...
Training Accuracy = 0.658
.......................
EPOCH 90 ...
Training Accuracy = 0.971
EPOCH 91 ...
Training Accuracy = 0.968
EPOCH 92 ...
Training Accuracy = 0.971
EPOCH 93 ...
Training Accuracy = 0.975
EPOCH 94 ...
Training Accuracy = 0.965
EPOCH 95 ...
Training Accuracy = 0.977
EPOCH 96 ...
Training Accuracy = 0.967
EPOCH 97 ...
Training Accuracy = 0.976
EPOCH 98 ...
Training Accuracy = 0.976
EPOCH 99 ...
Training Accuracy = 0.976
EPOCH 100 ...
Training Accuracy = 0.977
【说明】因时间关系,我这里只训练100次,看来精度也还可以,如果增加迭代次数,可以达到99%左右
8)用测试数据验证模型
|
1 2 3 4 5 6 7 8 |
with tf.Session() as sess: # restore saved session with highest validation accuracy saver.restore(sess, './checkpoints/traffic_sign_model.ckpt-99') test_accuracy = evaluate(X_test_norm, y_test) print('Performance on test set: {:.3f}'.format(test_accuracy)) INFO:tensorflow:Restoring parameters from ./checkpoints/traffic_sign_model.ckpt-99 Performance on test set: 0.911 |
26.3 实例2(使用LeNet神经网络)
待续



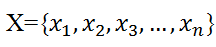
 含义依次类推。
含义依次类推。
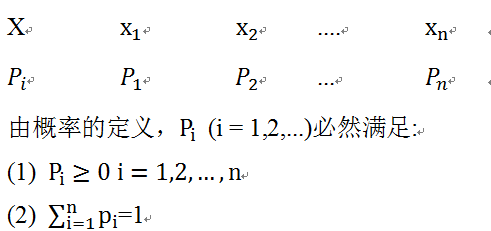

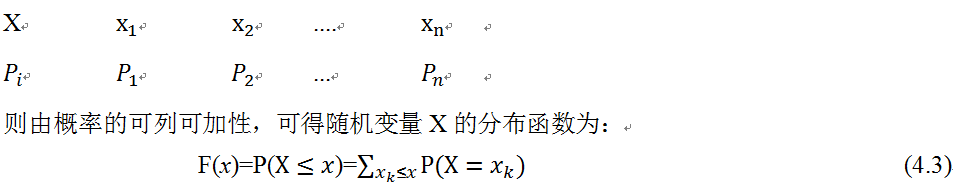
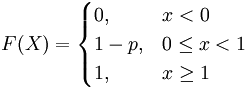


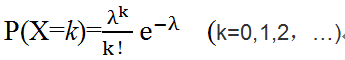




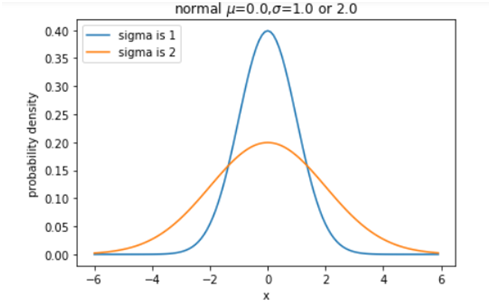
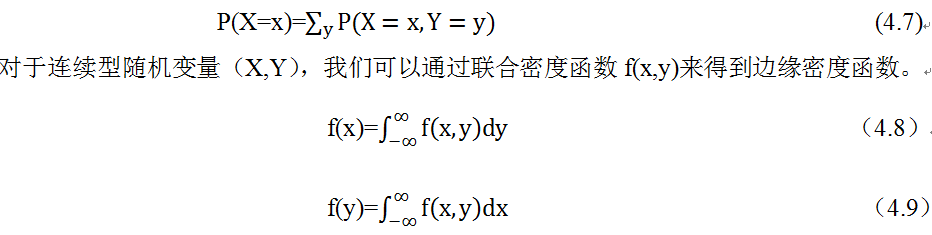




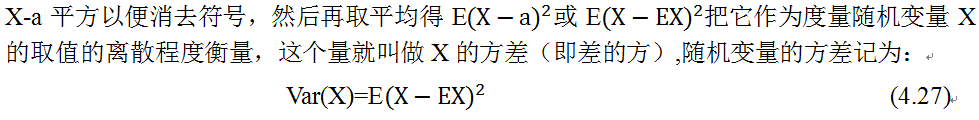

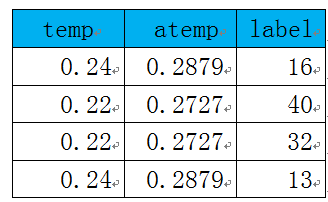
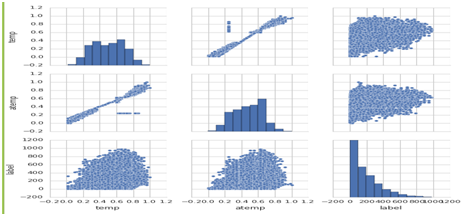

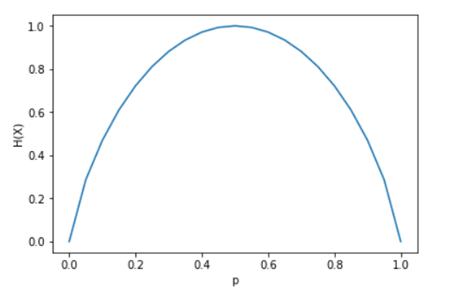
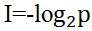 。为此,可能有人会问,为何要用对数,前面还要带上负号?
。为此,可能有人会问,为何要用对数,前面还要带上负号?