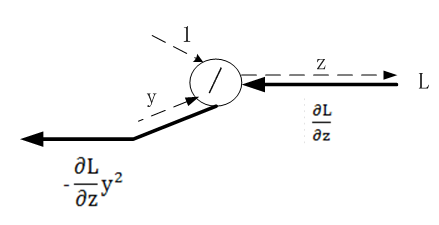
24.1 链式法则
假设z=f(t)
t=g(y)
则,根据复合函数的求导规则(即链式法则),可得:

24.1.1 计算图的方向传播
反向传播的计算顺序是将信号E乘以节点的局部导数(∂y/∂x),然后将结果传递给下一个节点。
24.1.2 链式法则
如果某个函数为复合函数,则该复合函数的导数可以用构成复合函数的各个函数的导数的乘积表示。
24.1.3 链式法则和计算图

反向传播是上游传过来的导数乘以本节点导数。
24.2 反向传播
反向传播是上游传过来的导数乘以本节点对应输入的导数。
24.2.1 加法节点的反向传播
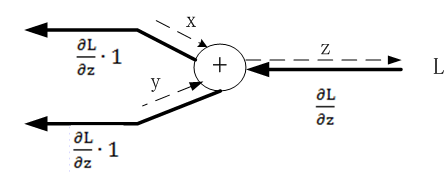
代码实现如下
|
1 2 3 4 5 6 7 8 9 |
class AddLayer: def __init__(self): pass def forward(self,x,y): return x+y def backward(self,dout): dx=dout*1 dy=dout*1 return dx,dy |
24.2.2 乘法法节点的反向传播
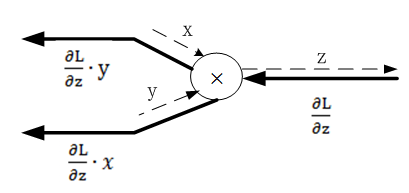
|
1 2 3 4 5 6 7 8 9 10 11 12 |
class MultiLayer: def __init__(self): self.x=None self.y=None def forward(self,x,y): self.x=x self.y=y return x*y def backward(self,dout): dx=dout*self.y dy=dout*self.x return dx,dy |
24.2.3 激活函数层的反向传播
24.3 激活函数层的反向传播
24.3.1 ReLU激活函数
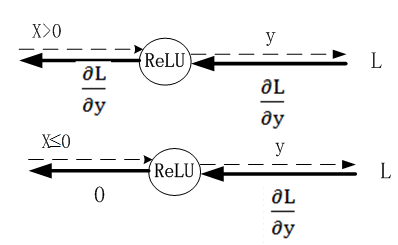
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
class ReLu: def __init__(self): self.mask=None def forward(self,x): self.mask=(x<=0) #把x中不大于0的置为True,否则为False。 out=x.copy() #使不大于0的设置为0,其它不变。 out[self.mask]=0 return out def backward(self,dout): dout[self.mask]=0 dx=dout return dx |
24.3.2 Sigmoid激活函数
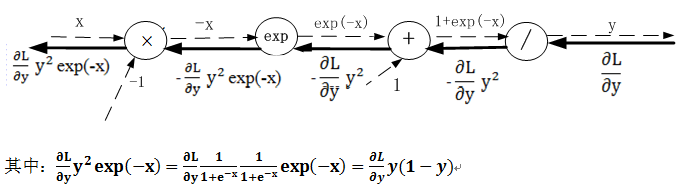
根据导数的链式规则,上游的值乘以本节点输出对输入的导数.
代码实现
|
1 2 3 4 5 6 7 8 9 10 |
class sigmoid: def __init__(self): self.out=None def forward(self,x): out=1/(1+np.exp(-x)) self.out=out return out def backward(self,dout): dx=dout*(1.0-self.out)*self.out return dx |
24.4 Affine/softmax层的反向传播
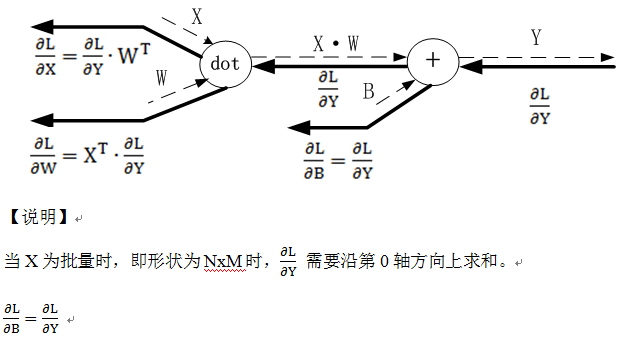
DY=np.array([[1,2,3],[4,5,6]])
dB=np.sum(DY,axis=0)
Affine层的代码实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
class Affine: def __init__(self,W,B): self.W=W self.B=B self.X=None self.dW=None self.dB=None def forward(self,X): self.X=X out=np.dot(X,self.W)+self.B return out def backward(self,dout): dX=np.dot(dout,self.W.T) self.dW=np.dot(self.X.T,dout) self.dB=np.sum(dout,axis=0) return dx |
24.4.1 Softmax-with loss 层
输入一张手写5的图片,经过多层(这里假设为2层)神经网络转换后,对输出10个节点,在各个输出节点的得分或概率是不同的,其中对应标签为5的节点(转换为one
-hot后为[0,0,0,0,1,0,0,0,0],得分或概率最大。

我们看一下带softmax及loss的反向传播,如何计算梯度。以下为示意图。
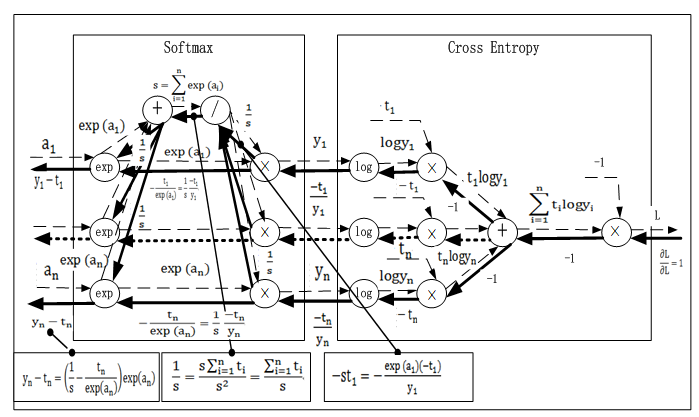
代码实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
class softmaxwithloss: def __init__(self): self.loss=None self.y=None self.t=None def forward(self,x,t): self.y=softmax(x) self.t=t self.loss=cross_entropy_error(self.y,self.t) return self.loss def backward(self,dout=1): #如果是批处理,需要除以批量数据 batch_size=self.t.shape[0] dx=(self.y-self.t)/batch_size return dx |
24.5 损失反向传播法的实现
24.5.1 神经网络学习的基本步骤
利用随机梯度下降法,求梯度并更新权重和偏置参数,整个过程是个循环过程。
步骤1
从训练数据中随机选择一部分数据
步骤2
构建网络,利用前向传播,求出输出值。然后利用输出值与目标值得到损失函数,利用损失函数,利用反向传播方法,求各参数的梯度。
步骤3
将权重参数沿梯度方向进行微小更新
步骤4
重复以上1、2、3步骤
24.5.2 神经网络学习的反向传播法的实现
神经网络结构图如下

下面用代码实现
1)概述
为定义和保存以上神经网络架构,需要先定义几个实例变量:
保存权重参数的字典型变量params。
保存各层的信息的顺序字典layers,这里的顺序是插入数据的先后顺序。
神经网络的最后一层lastlayer
除了以上三个实例变量,还需要定义一些方法
构造函数,以初始化变量和权重等
预测方法,根据神经网络各层的前向传播得到最后的输出值
损失函数,根据输出值与目标值,得到交叉熵作为衡量两个分布的距离。
评估指标,这里使用精度来衡量模型性能
最后就是计算梯度,这里使用反向传播方法的得到,具体是利用导数的链式法则,从后往前,获取各层的梯度作为前层梯度往前传递(往输入端)
当然,这里需要先定义好各层类,各类中各层的权重参数、包括前向传播结果,反向传播的梯度等。
2)定义各层类
①softmax 函数及Sigmoid类
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
def softmax(x): if x.ndim == 2: x = x.T x = x - np.max(x, axis=0) y = np.exp(x) / np.sum(np.exp(x), axis=0) return y.T x = x - np.max(x) #防止出现溢出情况 return np.exp(x) / np.sum(np.exp(x)) class Sigmoid: def __init__(self): self.out=None def forward(self,x): self.out=1 / (1 + np.exp(-x)) return self.out def backward(self,dout): dx=dout*(1.0 -self.out) * self.out return dx class Relu: def __init__(self): self.mask = None def forward(self, x): self.mask = (x <= 0) out = x.copy() out[self.mask] = 0 return out def backward(self, dout): dout[self.mask] = 0 dx = dout return dx |
②Affine类或称为sumweigt
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
class Affine: def __init__(self, W, b): self.W =W self.b = b self.x = None self.original_x_shape = None # 权重和偏置参数的导数 self.dW = None self.db = None def forward(self, x): # 对应张量 self.original_x_shape = x.shape x = x.reshape(x.shape[0], -1) self.x = x out = np.dot(self.x, self.W) + self.b return out def backward(self, dout): dx = np.dot(dout, self.W.T) self.dW = np.dot(self.x.T, dout) self.db = np.sum(dout, axis=0) dx = dx.reshape(*self.original_x_shape) # 还原输入数据的形状(对应张量) return dx |
③最后一层
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
class SoftmaxWithLoss: def __init__(self): self.loss = None self.y = None # softmax的输出 self.t = None # 监督数据 def forward(self, x, t): self.t = t self.y = softmax(x) self.loss = cross_entropy_error(self.y, self.t) return self.loss def backward(self, dout=1): batch_size = self.t.shape[0] if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况 dx = (self.y - self.t) / batch_size else: dx = self.y.copy() dx[np.arange(batch_size), self.t] -= 1 dx = dx / batch_size return dx |
3)定义损失函数
|
1 2 3 4 5 6 7 8 9 10 11 |
def cross_entropy_error(y, t): if y.ndim == 1: t = t.reshape(1, t.size) y = y.reshape(1, y.size) # 如果t为one-hot格式,把它转换为数字格式 if t.size == y.size: t = t.argmax(axis=1) batch_size = y.shape[0] return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-8)) / batch_size |
4)定义神经网络类
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
import numpy as np from collections import OrderedDict class TwoLayerNet: def __init__(self, input_size, hidden_size,output_size, weight_init_std = 0.01): # 初始化权重 self.params = {} self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size) self.params['b1'] = np.zeros(hidden_size) self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size) self.params['b2'] = np.zeros(output_size) # 生成层 self.layers = OrderedDict() self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1']) #self.layers['Sigmoid1'] = Sigmoid() self.layers['Relu1'] = Relu() self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2']) self.lastLayer = SoftmaxWithLoss() def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x # x:输入数据, t:监督数据 def loss(self, x, t): y = self.predict(x) return self.lastLayer.forward(y, t) def accuracy(self, x, t): y = self.predict(x) y = np.argmax(y, axis=1) #print("预测值",y[0],y.shape) if t.ndim != 1: t = np.argmax(t, axis=1) accuracy = np.sum(y == t) / float(x.shape[0]) return accuracy # x:输入数据, t:监督数据 def numerical_gradient(self, x, t): loss_W = lambda W: self.loss(x, t) grads = {} grads['W1'] = numerical_gradient(loss_W, self.params['W1']) grads['b1'] = numerical_gradient(loss_W, self.params['b1']) grads['W2'] = numerical_gradient(loss_W, self.params['W2']) grads['b2'] = numerical_gradient(loss_W, self.params['b2']) return grads def gradient(self, x, t): # forward self.loss(x, t) # backward dout = 1 dout = self.lastLayer.backward(dout) layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) # 用一个字典记录各参数(权重和偏置)的梯度 grads = {} grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db return grads |
5)使用误差反向传播法训练模型
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
import numpy as np import matplotlib.pyplot as plt # 读入数据 (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True) network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10) iters_num = 20000 # 适当设定循环的次数 train_size = x_train.shape[0] batch_size = 100 learning_rate = 0.1 train_loss_list = [] train_acc_list = [] test_acc_list = [] iter_per_epoch = max(train_size / batch_size, 1) for i in range(iters_num): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] # 计算梯度 #grad = network.numerical_gradient(x_batch, t_batch) grad = network.gradient(x_batch, t_batch) for key in ('W1', 'b1', 'W2', 'b2'): network.params[key] -= learning_rate * grad[key] loss = network.loss(x_batch, t_batch) train_loss_list.append(loss) if i % iter_per_epoch == 0: # 更新 if i%5000==0: learning_rate*=0.9 # 更新参数 print(learning_rate) train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) train_acc_list.append(train_acc) test_acc_list.append(test_acc) print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc)) # 绘制图形 markers = {'train': 'o', 'test': 's'} x = np.arange(len(train_acc_list)) plt.plot(x, train_acc_list, label='train acc') plt.plot(x, test_acc_list, label='test acc', linestyle='--') plt.xlabel("epochs") plt.ylabel("accuracy") plt.ylim(0, 1.0) plt.legend(loc='lower right') plt.show() |
.09000000000000001
train acc, test acc | 0.9837833333333333, 0.9724
0.09000000000000001
train acc, test acc | 0.9842666666666666, 0.9722
0.08100000000000002
train acc, test acc | 0.98475, 0.9716
0.08100000000000002
train acc, test acc | 0.9853166666666666, 0.9733
0.08100000000000002
train acc, test acc | 0.9859666666666667, 0.9726
0.08100000000000002
train acc, test acc | 0.9861166666666666, 0.9707
0.08100000000000002
train acc, test acc | 0.9873, 0.9737
0.08100000000000002
train acc, test acc | 0.9873833333333333, 0.9744
0.08100000000000002
train acc, test acc | 0.9881, 0.973
0.08100000000000002
train acc, test acc | 0.9886666666666667, 0.9747
0.08100000000000002
train acc, test acc | 0.9888833333333333, 0.9743
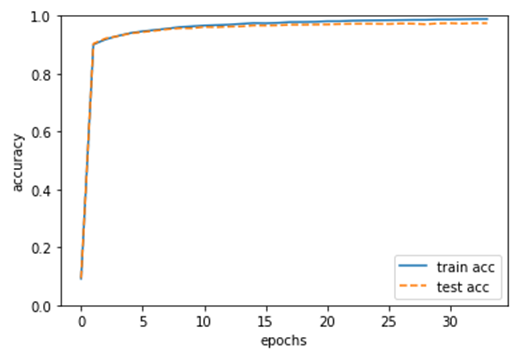
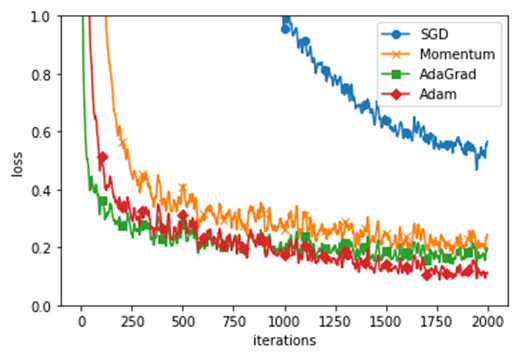
6)利用各种算法对MNIST数据集的影响
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
def smooth_curve(x): """用于使损失函数的图形变圆滑 参考:http://glowingpython.blogspot.jp/2012/02/convolution-with-numpy.html """ window_len = 11 s = np.r_[x[window_len-1:0:-1], x, x[-1:-window_len:-1]] w = np.kaiser(window_len, 2) y = np.convolve(w/w.sum(), s, mode='valid') return y[5:len(y)-5] import matplotlib.pyplot as plt # 0:读入MNIST数据========== (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) train_size = x_train.shape[0] batch_size = 128 max_iterations = 2000 # 1:进行实验的设置========== optimizers = {} optimizers['SGD'] = SGD() optimizers['Momentum'] = Momentum() optimizers['AdaGrad'] = AdaGrad() optimizers['Adam'] = Adam() #optimizers['RMSprop'] = RMSprop() networks = {} train_loss = {} for key in optimizers.keys(): networks[key] = TwoLayerNet( input_size=784, hidden_size=100, output_size=10) train_loss[key] = [] # 2:开始训练========== for i in range(max_iterations): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] for key in optimizers.keys(): grads = networks[key].gradient(x_batch, t_batch) optimizers[key].update(networks[key].params, grads) loss = networks[key].loss(x_batch, t_batch) train_loss[key].append(loss) if i % 100 == 0: print( "===========" + "iteration:" + str(i) + "===========") for key in optimizers.keys(): loss = networks[key].loss(x_batch, t_batch) print(key + ":" + str(loss)) # 3.绘制图形========== markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"} x = np.arange(max_iterations) for key in optimizers.keys(): plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key) plt.xlabel("iterations") plt.ylabel("loss") plt.ylim(0, 1) plt.legend(loc='upper right') plt.show() |