月度归档：2019年12月

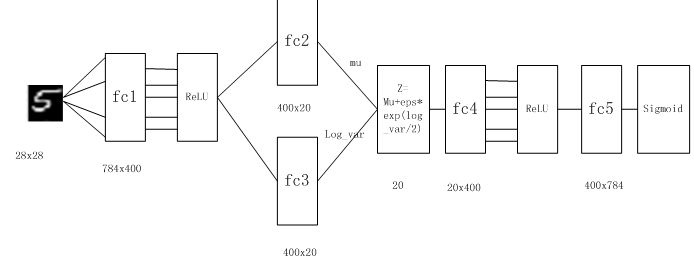
6.4前馈神经网络

前馈神经网络(Feedforward Neural Network)是最早被提出的神经网络，我们熟知的单层感知机、多层感知机、卷积深度网络等都属于前馈神经网络，它之所以称为前馈（Feedforward），或许与其信息往前流有关：数据从输入开始，流过中间计算过程，最后达到输出层。模型的输出和模型本身没有反馈(Feedback)连接。有反馈连接的称为反馈神经网络，如循环神经网络(Recurrent neural network，简称为RNN),RNN将在第15章介绍。本书如果没有特别说明，神经网络一般指前馈神经网络。
前面我们介绍了机器学习中几种常用算法，如线性模型、SVM、集成学习等有监督学习，这些算法我们都可以用神经网络来实现，如图6-22所示，神经网络的万能近似定理(universal approximation theorem)为重要理论依据。如果用神经网络来实现，还有很多便利，可自动获取特征、自动(或半自动)选择模型函数等。神经网络可以解决传统机器学习问题，更可以解决传统机器学习无法解决或难以解决的问题。因此，近些年神经网络发展非常快、应用也非常广。

图6-22线性模型的神经元
神经网络是深度学习的重要基础，深度学习中的深一般指神经网络的层次较深。接下来我们从最简单也最基础的神经元开始，然后介绍单层感知机、单层感知机的局限性、多层感知机、构建一个多层神经网络、前向传播及反向传播算法及实例等内容。

6.4.1神经元结构

1943年，心理学家McCulloch和数学家Pitts参考了生物神经元的结构(请看图6-23)，发表了抽象的神经元模型MP。一个神经元模型包含输入、计算、输出等功能。图6-23是一个典型的神经元模型：包含有3个输入、1个输出、计算功能（先求和，然后把求和结果传递给激活函数f）。

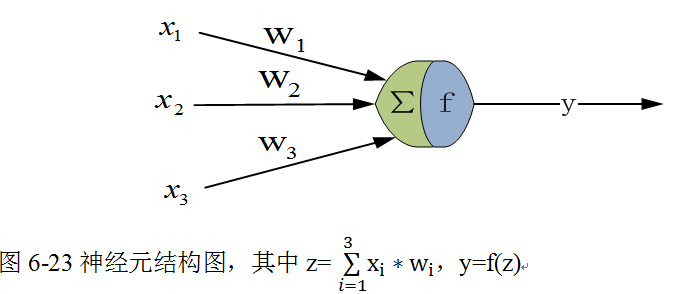
其间的箭头线称为“连接”。每个连接上有一个“权值”，如上图〖的w〗_i，权重是最重要的东西。一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。
我们使用x来表示输入，用w来表示权值。一个表示连接的有向箭头可以这样理解：在初端，传递的信号大小仍然是x，中间有加权参数w，经过这个加权后的信号会变成x*w，因此在连接的末端，信号的大小就变成了x*w。
输出y是在输入和权值的线性加权及叠加了一个函数f后的值。在MP模型里，函数f又称为激活函数,激活函数将数据压缩到一定范围区间内，其值大小将决定该神经元是否处于活跃状态。
从机器学习的角度，我们习惯把输入称为特征，输出y=f(z)为目标函数。
在6.1.1.小节介绍的逻辑回归实际上就是一个神经元结构，输入为x，参数有w（权重），b(偏移量)，求和得到：z=wx+b ，式（6.5）中函数f就是激活函数，该激活函数为阶跃函数。

6.4.2感知机的局限

在讲感知机的局限之前，我们先简单介绍一下感知机。在感知机中，“输入”也作为神经元节点，标为“输入单元”。感知机仅有两个层：分别是输入层和输出层。输入层里的“输入单元”只负责传输数据，不做计算。输出层里的“输出单元”则需要对前面一层的输入进行计算。
图6-24就是一个简单的感知机模型，输入层有3个输入单元，输出层有2个神经元。

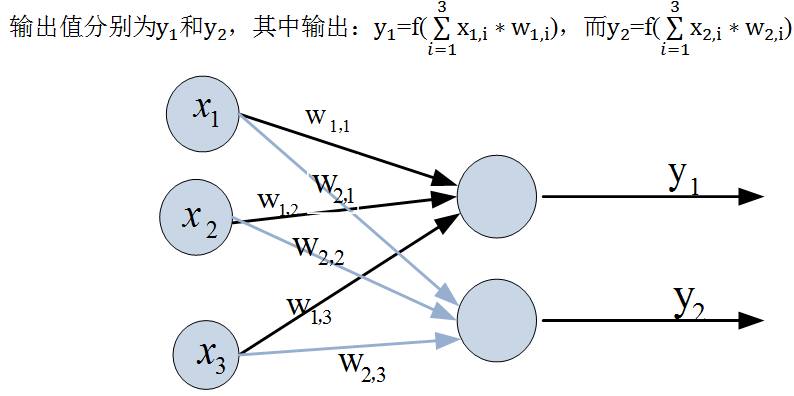
图6-24感知机模型
如果我们把输入的变量x_1、x_2、x_3用向量X来表示，即X=[x_1,x_2,x_3 ]^T。权重构成一个2*3矩阵 W（第一行下标为1开头的权重，第2行下标为2开头的权重）,输出表示为Y=[y_1，y_2 ]^T。这样输出公式可以改写成：
Y= f(W * X)（6.29）
其中f是激活函数。对激活函数，一般要求：
1)非线性：为提高模型的学习能力，如果是线性，那么再多层都相当于只有两层效果；
2)可微性：有时可以弱化，在一些点存在偏导即可；
3)单调性：保证模型简单。
与神经元模型不同，感知器中的权值是通过训练得到的。如何训练？这主要通过前向传播和反向传播，具体操作后续将详细介绍。感知器对线性可分或近似线性可分数据有很好效果，对线性不可分数据效果不理想。Minsky在1969年出版了叫《Perceptron》的一本书，里面用详细的数学证明了感知器无法解决XOR（异或）分类问题。这应该是比较简单的分类问题，用传统的机器学习算法如SVM等能很好解决，用感知器却无法解决。当时很多人做过多种尝试，如增加输出层的神经个数、调整激活函数等，但结果都不尽人意。后来有人通过增加层数，问题就迎刃而解。接下来我们介绍多层神经网络。

6.4.3多层神经网络

解决XOR问题也不是一帆风顺，增加层实际上很多人都想到了。但增加层以后，计算量、计算的复杂度就上来了，还有如何缩小误差，如何求最优解等问题也自然而然地出现。传统机器学习中我们可以通过梯度下降或最小二乘法等算法解决，但对神经网络如何优化，困扰大家很长时间。
直到1986年，Hinton和Rumelhar等人提出了反向传播（Backpropagation，简称BP）算法，解决了两层神经网络所需要的复杂计算量问题，从而带动了业界使用两层神经网络研究的热潮。目前，大量介绍神经网络的教材，一般重点介绍两层（带一个隐藏层）或多层神经网络的内容。
多层神经网络（含一层或多层隐含层）结构与神经元有何区别呢？图6-25就是一个简单的多层神经网络，除有一个输入层，一个输出层外，中间还有一层，这中间层因看不见其输入或输出数据，所以称为隐含层。

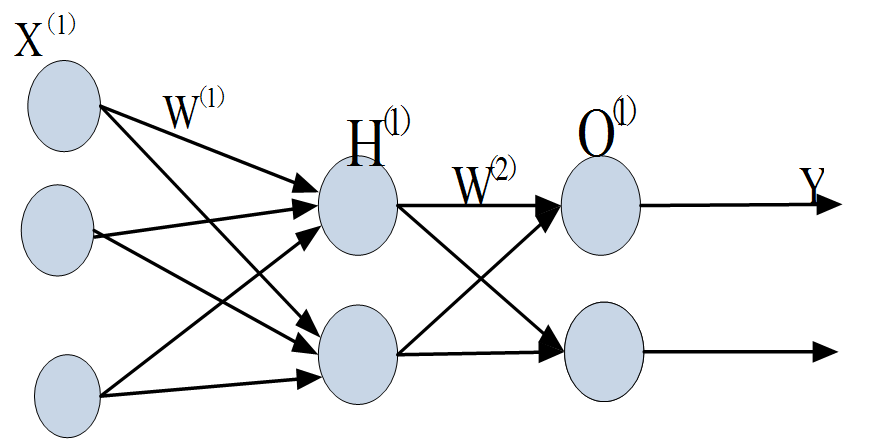
图6-25多层神经网络示意图
现在，我们的权值矩阵增加到了两个，我们用上标来区分不同层次之间的变量。
这里我们使用向量和矩阵来表示层次中的变量，如输入层表示为X^((1)),隐含层为H^((1))，O^((1))是为输出层。W^((1))和W^((2))是网络的矩阵参数。用矩阵来描述，可得到如下计算公式：
f(W^((1))*X^((1)))=H^((1))（6.29）
f(W^((2))*H^((1)))=O^((1))（6.30）
接下来，我们看多层神经网络如何处理XOR问题。
1）首先我们来看，何为XOR问题。

表6-2 异或问题

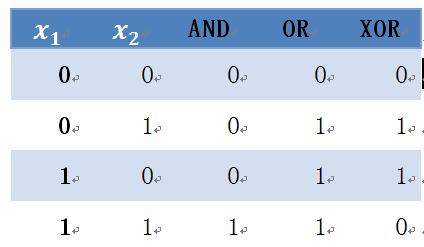
表6-2 可视化结果为图6-26,其中圆点表示0，方块表示1。AND、OR、NAND问题都是线性可分，但XOR是线性不可分。

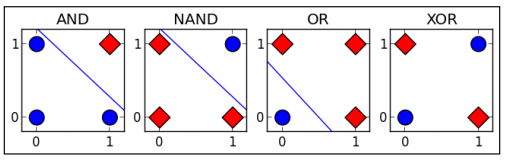
图6-26异或问题示意图
2）构建多层网络
（1）确定网络结构

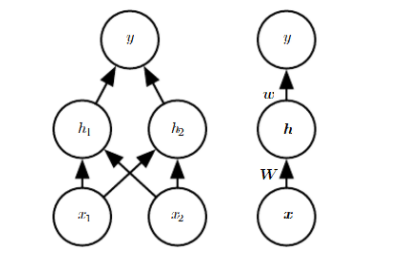
图6-27解决XOR问题的网络结构，左边为详细结构，右边为向量式结构，这种结构比较简洁，而且更贴近矩阵运算模型。
（2）确定输入
由表6-2可知，输入数据中有两个特征：x_1,x_2，共有4个样本。分别为〖[0,0]〗^T,〖[0,1]〗^T,〖 [1,0]〗^T,〖[1,1]〗^T，详细内容见表6-2。取x_1,x_2两列，每行代表一个样本，每个样本x都是一个向量，如果用矩阵表示就是：

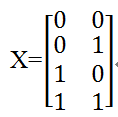
（3）确定隐含层及初始化权重矩阵W、w
隐含层主要确定激活函数，这里我们采用整流线性激活函数： g(z)=max{0,z}，如图6-28所示。

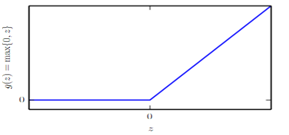
图6-28整流线性激活函数(ReLU)图形
初始化以下矩阵：

(5)计算

这样神经网络就得到我们希望的结果。
如何用程序如何实现XOR呢？下节将具体说明。

6.4.4实例：用TensorFlow实现XOR

上节通过一个实例具体说明了如何用多层神经网络来解决XOR问题，不过在计算过程中我们做了很多人工设置，如对权重及偏移量的设置。如果用程序来实现，一般不会这样，如果维度较多，手工设置参数也是不现实的。接下来我们介绍如何用TensorFlow来实现XOR问题。用程序实现，总的思路是：用反向传播算法（BP），循环迭代，直到满足终止条件为止。如果你对BP算法不熟悉，下节将详细介绍。具体步骤如下：
（1）明确输入数据、目标数据

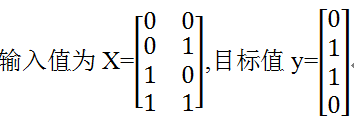
（2）确定网络架构
网络架构采用图6-27
（3）确定几个函数
激活函数、代价函数、优化算法等。这里激活函数还是使用ReLU函数，代价函数使用MSE，优化器使用Adam自适应算法。
（4）初始化权重和偏移量等参数
初始化权重和偏移量，只要随机取些较小值即可，无须考虑一些特殊值，最终这些权重值或偏移量，在循环迭代中不断更新。随机生成权重初始化数据，生成的数据符合正态分布。
（5）循环迭代
循环迭代过程中参数会自动更新
（6）最后打印输出
以下我们用TensorFlow来实现XOR问题的详细代码，为尽量避免循环，这里采用矩阵思维，这样可以大大提升性能，尤其在深度学习环境中。如果你对TensorFlow还不是很熟悉，可以先跳过，或先看一下第9章。

import tensorflow as tf
import numpy as np

#定义输入与目标值
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
Y = np.array([[0], [1], [1], [0]])

#定义占位符，从输入或目标中按行取数据
x = tf.placeholder(tf.float32, [None, 2])
y = tf.placeholder(tf.float32, [None, 1])
#初始化权重，使权重满足正态分布
#w1是输入层到隐含层间的权重矩阵，w2是隐含层到输出层的权重
w1 = tf.Variable(tf.random_normal([2,2]))
w2 = tf.Variable(tf.random_normal([2,1]))
#定义偏移量，b1为隐含层上偏移量，b2是输出层上偏移量。
b1=tf.Variable([0.1,0.1])
b2=tf.Variable(0.1)

#利用激活函数就隐含层的输出值
h=tf.nn.relu(tf.matmul(x,w1)+b1)
#计算输出层的值
out=tf.matmul(h,w2)+b2

#定义代价函数或代价函数
loss = tf.reduce_mean(tf.square(out - y))
#利用Adam自适应优化算法
train = tf.train.AdamOptimizer(0.1).minimize(loss)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(2000):
        sess.run(train, feed_dict={x: X, y: Y})
        loss_ = sess.run(loss, feed_dict={x: X, y: Y})
        if i%200==0 :
            print("step: %d, loss: %.3f"%(i, loss_))
    print("X: %r"%X)
    print("pred: %r"%sess.run(out, feed_dict={x: X}))

import tensorflow as tf

import numpy as np

#定义输入与目标值

X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])

Y = np.array([[0], [1], [1], [0]])

#定义占位符，从输入或目标中按行取数据

x = tf.placeholder(tf.float32, [None, 2])

y = tf.placeholder(tf.float32, [None, 1])

#初始化权重，使权重满足正态分布

#w1是输入层到隐含层间的权重矩阵，w2是隐含层到输出层的权重

w1 = tf.Variable(tf.random_normal([2,2]))

w2 = tf.Variable(tf.random_normal([2,1]))

#定义偏移量，b1为隐含层上偏移量，b2是输出层上偏移量。

b1=tf.Variable([0.1,0.1])

b2=tf.Variable(0.1)

#利用激活函数就隐含层的输出值

h=tf.nn.relu(tf.matmul(x,w1)+b1)

#计算输出层的值

out=tf.matmul(h,w2)+b2

#定义代价函数或代价函数

loss = tf.reduce_mean(tf.square(out - y))

#利用Adam自适应优化算法

train = tf.train.AdamOptimizer(0.1).minimize(loss)

with tf.Session() as sess:

sess.run(tf.global_variables_initializer())

for i in range(2000):

sess.run(train, feed_dict={x: X, y: Y})

loss_ = sess.run(loss, feed_dict={x: X, y: Y})

if i%200==0 :

print("step: %d, loss: %.3f"%(i, loss_))

print("X: %r"%X)

print("pred: %r"%sess.run(out, feed_dict={x: X}))

打印结果
step: 0, loss: 0.212
step: 200, loss: 0.000
step: 400, loss: 0.000
step: 600, loss: 0.000
step: 800, loss: 0.000
step: 1000, loss: 0.000
step: 1200, loss: 0.000
step: 1400, loss: 0.000
step: 1600, loss: 0.000
step: 1800, loss: 0.000
X: array([[0, 0],
[0, 1],
[1, 0],
[1, 1]])
pred: array([[ -7.44201316e-07],
[ 9.99997079e-01],
[ 9.99997139e-01],
[ -7.44201316e-07]], dtype=float32)

6.4.5反向传播算法

上节我们用TensorFlow实现了XOR问题，效果不错。整个训练过程就是通过循环迭代，逐步使代价函数值越来越小。如何使代价函数值越来越小？主要采用BP算法。BP算法是目前训练神经网络最常用且最有效的算法，也是整个神经网络的核心之一，它由前向和后向两个操作构成，其主要思想是：
（1）利用输入数据及当前权重，从输入层经过隐藏层，最后达到输出层，求出预测结果，并利用预测结果与真实值构成代价函数，这是前向传播过程；
（2）利用代价函数，将误差从输出层向隐藏层反向传播，直至传播到输入层，利用梯度下降法，求解参数梯度并优化参数；
（3）在反向传播的过程中，根据误差调整各种参数的值；不断迭代上述过程，直至收敛。
这样说，或许你觉得还不够具体、不好理解，没关系。BP算法确实有点复杂、不易理解，接下来，我们将以单个神经元如何实现BP算法为易撕口，由点扩展到面、由特殊推广到一般的神经网络，这样或许能大大降低学习BP算法的坡度。

1.单个神经元的BP算法

以下推导要用到微积分中链式法则，这里先简单介绍一下。链式法则用于计算复合函数，而BP算法需要利用链式法则。设x是实数，假设y=g(x),z=f(y)=f(g(x)),
根据链式法则，可得：

如果用向量表示，式（6.32）可简化为：

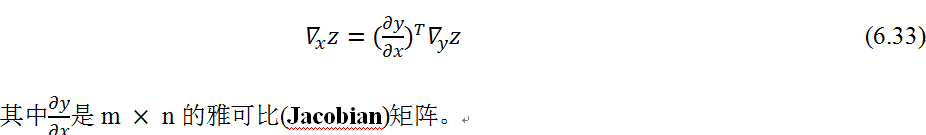
我们以单个神经元为例，以下是详细步骤。
（1）定义神经元结构
首先我们看只有一个神经元的BP过程。假设这个神经元有三个输入，激活函数为sigmoid函数：
f(x)=1/(1+e^(-x) ) （6.34）
其结构如图6-29所示

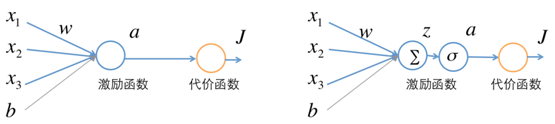
图6-29单个神经元，把左图中的神经元展开就得到右图。
（2）进行前向传播，从输入数据及权重开始，往输出层传递，最后求出预测值a，并与目标值y构成代价函数J。
假设一个训练样本为(x,y)，其中x是输入向量，x=[x_1,x_2,x_3 ]^T，y是目标值。先把输入数据与权重w=[w_1,w_2,w_3]乘积和求得z，然后通过一个激励函数sigmoid，得到输出a，最后a与y构成代价函数J。具体前向传播过程如下：

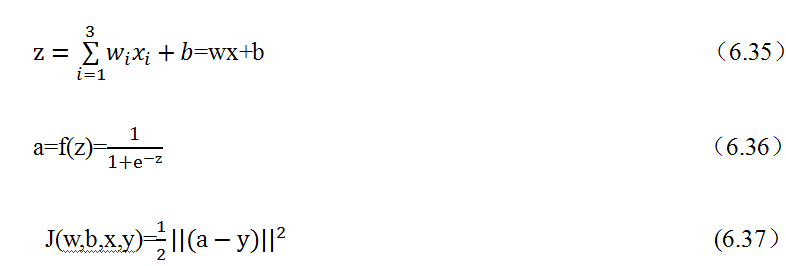
（3）进行反向传播，以代价函数开始，从输出到输入，求各节点的偏导。这里分成两步，先求J对中间变量的偏导，然后求关于权重w及偏移量b的偏导。先求J关于中间变量a和z的偏导：

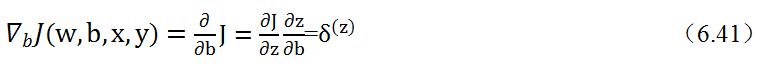
在这个过程中，先求∂J/∂a,进一步求∂J/∂z,最后求得∂J/∂w和∂J/∂b，然后利用梯度下降优化算法，变更参数权重参数w及偏移量b，结合上图(6.27)及链导法则，可以看出这是一个将代价函数的增量∂J自后向前传播的过程，因此称为反向传播。
（4）重复第（2）看代价函数J的误差是否满足要求或是否到指定迭代步数，如果不满足条件，继续（3），如此循环，直到满足条件为止。
这节介绍了单个神经元的BP算法。虽然只有一个神经元，但包括了BP的主要内容，正所谓“麻雀虽小，五脏俱全”。不过与一般神经网络还是有点区别，下节我们介绍一个三层神经网络的BP算法。

2.多层神经网络的BP算法

不失一般性，这里我们介绍一个含隐含层，两个输入，两个输出的神经网络，如图6-30。

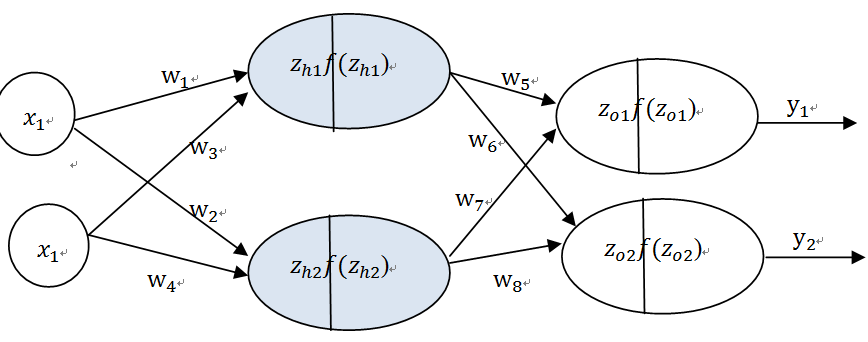
为简便起见，这里省略偏差b，这个实际可以看做X_n*w_n (X_n=1，w_n=b)。激活函数为f(z)=1/(1+e^(-z) ), 共有三层：第一层为输入层，第二层为隐含层，第三层为输出层，详解结构如图6-30。

输入层(x) 隐含层(h) 输出层(o)
图6-31多层神经网络
整个过程与单个神经元的基本相同，包括前向传播和反向传播两步，只是在求偏导时有些区别。
1）前向传播
把当前的权重参数和输入数据，从下到上（即从输入层到输出层），求取预测结果，并利用预测结果与真实值求解代价函数的值。如图6-32：

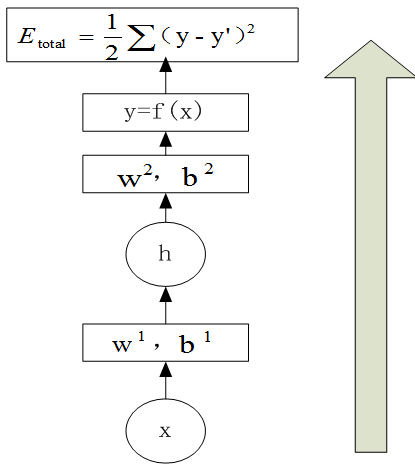
图6-32前向传播示意图

具体步骤如下：
(1) 从输入层到隐含层

(2)从隐含层到输出层

（3）计算总误差

2)反向传播
反向传播是利用前向传播求解的代价函数，从上到下（即从输出层到输入层），求解网络的参数梯度或新的参数值，经过前向和反向两个操作后，完成了一次迭代过程，如图6-33。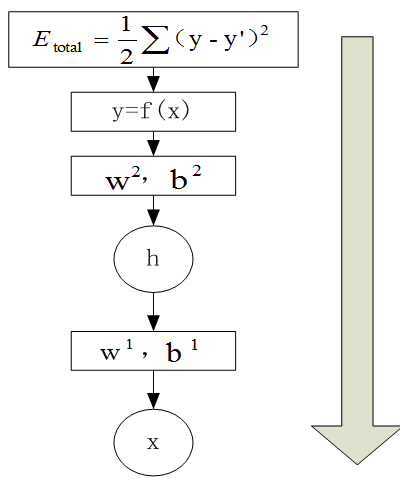

图6-33反向传播示意图
具体步骤如下：
（1）计算总误差

（2）由输出层到隐含层，假设我们需要分析权重参数w_5对整个误差的影响，可以用整体误差对w_5求偏导求出：这里利用微分中的链式法则，涉及过程包括：f(z_O1)--->z_O1----->w_5

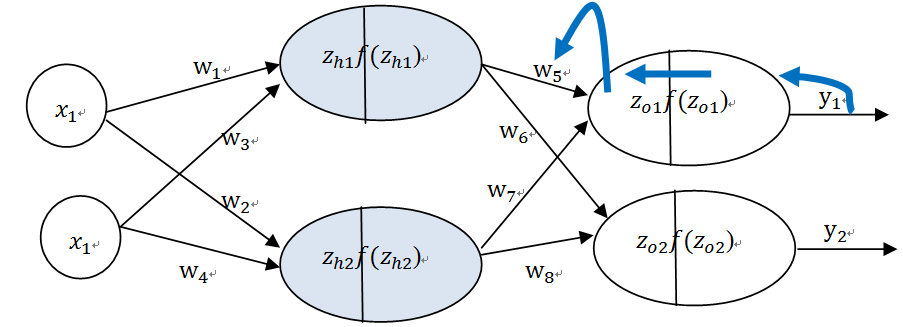
图6-34反向传播有输出层到权重w_5

根据式6.42--6.52，不难求出其他权重的偏导数。

（3）由隐含层到输入层，假设我们需要分析权重参数w_1对整个误差的影响，可以用整体误差对w_1求偏导，过程包括：f(z_h1)--->z_h1----->w_1，不过而f(z_h1)会接受E_o1和E_o2两个地方传来的误差，所以这个地方两个都要计算。

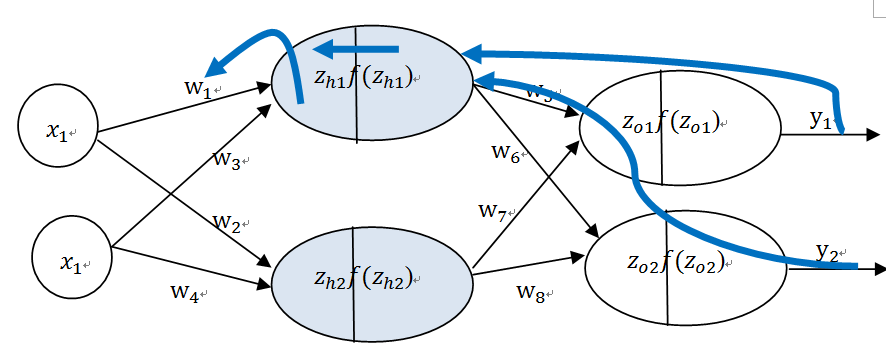
输入层(x) 隐含层(h)输出层(o)
图6-35反向传播由隐含层再到权重w_1
代价函数偏导由隐含层到权重w_1，计算如下：

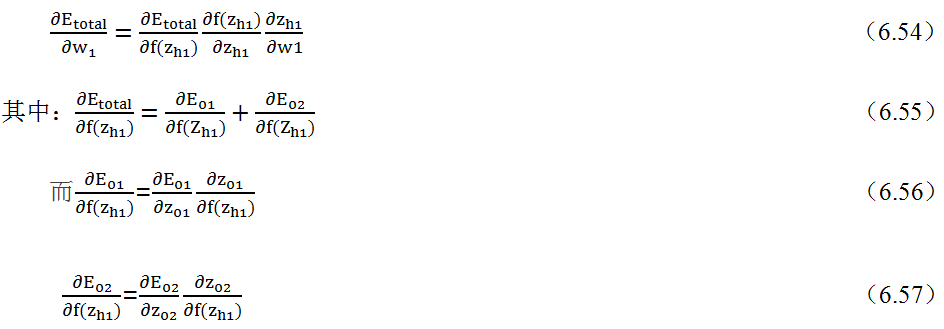
至此，可求得权重w_1的偏导数，按类似方法，可得到其他权重的偏导。权重和偏移量的偏导求出后，再根据梯度优化算法，更新各权重和偏移量。
3）判断是否满足终止条件
根据更新后的权重、偏移量，进行前向传播，计算输出值及代价函数，根据误差要求或迭代次数，看是否满足终止条件，满足则终止，否则，继续循环以上步骤。
现在很多架构都提供了自动微分功能，在具体训练模型时，只需要选择优化器及代价函数，其他无须过多操心。但是，理解反向传播算法的原理对学习深度学习的调优、架构设计等还是非常有帮助的。

6.5 实例：用keras构建深度学习架构

最后给出一个用Keras实现的样例，这里用Keras主要考虑其简洁性，Keras的介绍可参考16.5节。如果你还想进一步了解Keras，可参考Keras中文网站http://keras-cn.readthedocs.io/en/latest/或飞谷云网站：http://www.feiguyunai.com/

#构建模型
model = Sequential()
#往模型中添加一层，神经元个数，激活函数及指明输入数据维度。
model.add(Dense(32, activation='relu', input_dim=784))
#再添加一层，神经元个数及激活函数
model.add(Dense(1, activation='sigmoid'))
#编译模型，指明所用优化器，代价函数及度量方式等
model.compile(optimizer='Adam',loss='binary_crossentropy',metrics=['accuracy'])
#训练模型，指明训练的数据集，循环次数，输出详细程度，批量大小等信息
model.fit(x_train, y_train, epochs=10,verbose=2, batch_size=32,)

#构建模型

model = Sequential()

#往模型中添加一层，神经元个数，激活函数及指明输入数据维度。

model.add(Dense(32, activation='relu', input_dim=784))

#再添加一层，神经元个数及激活函数

model.add(Dense(1, activation='sigmoid'))

#编译模型，指明所用优化器，代价函数及度量方式等

model.compile(optimizer='Adam',loss='binary_crossentropy',metrics=['accuracy'])

#训练模型，指明训练的数据集，循环次数，输出详细程度，批量大小等信息

model.fit(x_train, y_train, epochs=10,verbose=2, batch_size=32,)

深度学习不仅在于其强大的学习能力，更在于它的创新能力。我们通过构建判别模型来提升模型的学习能力，通过构建生成模型来发挥其创新能力。判别模型通常利用训练样本训练模型,然后利用该模型，对新样本x，进行判别或预测。而生成模型正好反过来，根据一些规则y，来生成新样本x。
生成式模型很多，本章主要介绍常用的两种：变分自动编码器(VAE)和生成式对抗网络(GAN)及其变种。虽然两者都是生成模型，并且通过各自的生成能力展现其强大的创新能力，但他们在具体实现上有所不同。GAN基于博弈论，目的是找到达到纳什均衡的判别器网络和生成器网络。而VAE基本根植贝叶斯推理，其目标是潜在地建模，从模型中采样新的数据。
本章主要介绍多种生成式网络，具体内容如下：
用变分自编码器生成图像
GAN简介
如何用GAN生成图像
比较VAE与GAN的异同
CGAN、DCGAN简介

8.1 用变分自编码器生成图像

变分自编码器是自编码器的改进版本，自编码器是一种无监督学习，但它无法产生新的内容，变分自编码器对其潜在空间进行拓展，使其满足正态分布，情况就大不一样了。

8.1.1 自编码器

自编码器是通过对输入X进行编码后得到一个低维的向量z，然后根据这个向量还原出输入X。通过对比X与X ̃的误差，再利用神经网络去训练使得误差逐渐减小，从而达到非监督学习的目的。图8-1 为自编码器的架构图:

图8-1 自编码器架构图
自编码器因不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。为解决这一问题，人们对潜在空间Z（潜在变量对应的空间）增加一些约束，使Z满足正态分布，由此就出现了VAE模型，VAE对编码器添加约束，就是强迫它产生服从单位正态分布的潜在变量。正是这种约束，把VAE和自编码器区分开来。

8.1.2变分自编码器

变分自编码器关键一点就是增加一个对潜在空间Z的正态分布约束，如何确定这个正态分布就成主要目标，我们知道要确定正态分布，只要确定其两个参数均值u和标准差σ。那么如何确定u、σ？用一般的方法或估计比较麻烦效果也不好，人们发现用神经网络去拟合，简单效果也不错。图8-2 为AVE的架构图。

图8-2 AVE架构图
在图8-2中，模块①的功能把输入样本X通过编码器输出两个m维向量（mu、log_var）,这两个向量是潜在空间（假设满足正态分布）的两个参数（相当于均值和方差）。那么如何从这个潜在空间采用一个点Z?
这里假设潜在正态分布能生成输入图像，从标准正态分布N(0,I)中采样一个ε（模块②的功能），然后使
Z=mu+ exp⁡(log_var)*ε （8.1）
这也是模块③的主要功能。
Z是从潜在空间抽取的一个向量，Z通过解码器生成一个样本X ̃，这是模块④的功能。
这里ε是随机采样的，这就可保证潜在空间的连续性、良好的结构性。而这些特性使得潜在空间的每个方向都表示数据中有意义的变化方向。
以上这些步骤构成整个网络的前向传播过程，反向传播如何进行？要确定反向传播就涉及到损失函数了，损失函数是衡量模型优劣的主要指标。这里我们需要从以下两个方面进行衡量。
（1）生成的新图像与原图像的相似度；
（2）隐含空间的分布与正态分布的相似度。
度量图像的相似度一般采用交叉熵(如nn.BCELoss)，度量两个分布的相似度一般采用KL散度(Kullback-Leibler divergence)。这两个度量的和构成了整个模型的损失函数。
以下是损失函数的具体代码，AVE损失函数的推导过程，有兴趣的读者可参考原论文：https://arxiv.org/pdf/1606.05908.pdf

# 定义重构损失函数及KL散度
reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())
#两者相加得总损失
loss= reconst_loss+ kl_div

# 定义重构损失函数及KL散度

reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)

kl_div = - 0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

#两者相加得总损失

loss= reconst_loss+ kl_div

8.1.3用变分自编码器生成图像

前面我们介绍了AVE的架构和原理，至此对AVE的“蓝图”就有了大致了解，如何实现这个蓝图？这节我们将结合代码，用Pytorch实现AVE。此外，还包括在实现过程中需要注意的一些问题，为便于说明起见，数据集采用MNIST,整个网络结构如图8-3所示。

图8-3 AVE网络结构图
首先，我们简单介绍一下实现的具体步骤，然后，结合代码详细说明，如何用Pytorch一步步实现AVE。具体步骤如下：
（1）导入必要的包

import os
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
from torchvision import transforms
from torchvision.utils import save_image

import os

import torch

import torch.nn as nn

import torch.nn.functional as F

import torchvision

from torchvision import transforms

from torchvision.utils import save_image

（2）定义一些超参数

image_size = 784
h_dim = 400
z_dim = 20
num_epochs = 30
batch_size = 128
learning_rate = 0.001

image_size = 784

h_dim = 400

z_dim = 20

num_epochs = 30

batch_size = 128

learning_rate = 0.001

（3）对数据集进行预处理，如转换为Tensor，把数据集转换为循环、可批量加载的数据集；

# 下载MNIST训练集，这里因已下载，故download=False
# 如果需要下载，设置download=True将自动下载
dataset = torchvision.datasets.MNIST(root='data',
                                     train=True,
                                     transform=transforms.ToTensor(),
                                     download=False)

#数据加载
data_loader = torch.utils.data.DataLoader(dataset=dataset,
                                          batch_size=batch_size, 
                                          shuffle=True)

# 下载MNIST训练集，这里因已下载，故download=False

# 如果需要下载，设置download=True将自动下载

dataset = torchvision.datasets.MNIST(root='data',

train=True,

transform=transforms.ToTensor(),

download=False)

#数据加载

data_loader = torch.utils.data.DataLoader(dataset=dataset,

batch_size=batch_size,

shuffle=True)

（4）构建AVE模型，主要由encode和decode两部分组成；

# 定义AVE模型
class VAE(nn.Module):
    def __init__(self, image_size=784, h_dim=400, z_dim=20):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, h_dim)
        self.fc2 = nn.Linear(h_dim, z_dim)
        self.fc3 = nn.Linear(h_dim, z_dim)
        self.fc4 = nn.Linear(z_dim, h_dim)
        self.fc5 = nn.Linear(h_dim, image_size)
        
    def encode(self, x):
        h = F.relu(self.fc1(x))
        return self.fc2(h), self.fc3(h)
    
    #用mu，log_var生成一个潜在空间点z，mu，log_var为两个统计参数，我们假设
    #这个假设分布能生成图像。
    def reparameterize(self, mu, log_var):
        std = torch.exp(log_var/2)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        h = F.relu(self.fc4(z))
        return F.sigmoid(self.fc5(h))
    
    def forward(self, x):
        mu, log_var = self.encode(x)
        z = self.reparameterize(mu, log_var)
        x_reconst = self.decode(z)
        return x_reconst, mu, log_var

# 定义AVE模型

class VAE(nn.Module):

def __init__(self, image_size=784, h_dim=400, z_dim=20):

super(VAE, self).__init__()

self.fc1 = nn.Linear(image_size, h_dim)

self.fc2 = nn.Linear(h_dim, z_dim)

self.fc3 = nn.Linear(h_dim, z_dim)

self.fc4 = nn.Linear(z_dim, h_dim)

self.fc5 = nn.Linear(h_dim, image_size)

def encode(self, x):

h = F.relu(self.fc1(x))

return self.fc2(h), self.fc3(h)

#用mu，log_var生成一个潜在空间点z，mu，log_var为两个统计参数，我们假设

#这个假设分布能生成图像。

def reparameterize(self, mu, log_var):

std = torch.exp(log_var/2)

eps = torch.randn_like(std)

return mu + eps * std

def decode(self, z):

h = F.relu(self.fc4(z))

return F.sigmoid(self.fc5(h))

def forward(self, x):

mu, log_var = self.encode(x)

z = self.reparameterize(mu, log_var)

x_reconst = self.decode(z)

return x_reconst, mu, log_var

（5）选择GPU及优化器

# 设置pytorch在哪块GPU上运行，这里假设使用序号为1的这块GPU.
torch.cuda.set_device(1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

# 设置pytorch在哪块GPU上运行，这里假设使用序号为1的这块GPU.

torch.cuda.set_device(1)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')

model = VAE().to(device)

optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

（6）训练模型，同时保存原图像与随机生成的图像；

with torch.no_grad():
        # 保存采样图像，即潜在向量Z通过解码器生成的新图像
        z = torch.randn(batch_size, z_dim).to(device)
        out = model.decode(z).view(-1, 1, 28, 28)
        save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

        # 保存重构图像，即原图像通过解码器生成的图像
        out, _, _ = model(x)
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
        save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

with torch.no_grad():

# 保存采样图像，即潜在向量Z通过解码器生成的新图像

z = torch.randn(batch_size, z_dim).to(device)

out = model.decode(z).view(-1, 1, 28, 28)

save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

# 保存重构图像，即原图像通过解码器生成的图像

out, _, _ = model(x)

x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)

save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

（7）展示原图像及重构图像

reconsPath = './ave_samples/reconst-30.png'
Image = mpimg.imread(reconsPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

reconsPath = './ave_samples/reconst-30.png'

Image = mpimg.imread(reconsPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

这是迭代30次的结果

图8-4 AVE构建图片
图8-4中，奇数列为原图像，偶数列为原图像重构的图像。从这个结果可以看出重构图像效果还不错。图8-5为由潜在空间通过解码器生成的新图像，这个图像效果也不错。
（8）显示由潜在空间点Z生成的新图像

genPath = './ave_samples/sampled-30.png'
Image = mpimg.imread(genPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

genPath = './ave_samples/sampled-30.png'

Image = mpimg.imread(genPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

图8-5 AVE新图片
这里构建网络主要用全连接层，有兴趣的读者，可以把卷积层，如果编码层使用卷积层(如nn.Conv2d)，解码器需要使用反卷积层(nn. ConvTranspose2d)。接下来我们介绍生成式对抗网络，并用该网络生成新数字，其效果将好于AVE生成的数字。

8.2 GAN简介

上节我们介绍了基于自动编码器的AVE，根据这个网络可以生成新的图像。这节我们将介绍另一种生成式网络，它是基于博弈论的，所以又称为生成式对抗网络（Generative adversarial nets，GAN）。它是2014年由Ian Goodfellow提出的，它要解决的问题是如何从训练样本中学习出新样本，训练样本是图片就生成新图片，训练样本是文章就输出新文章等等。
GAN既不依赖标签来优化，也不是根据对结果奖惩来调整参数。它是依据生成器和判别器之间的博弈来不断优化。打个不一定很恰当的比喻，就像一台验钞机和一台制造假币的机器之间的博弈，两者不断博弈，博弈的结果假币越来越像真币，直到验钞机无法识别一张货币是假币还是真币为止。这样说，还是有点抽象，接下来我们将从多个侧面进行说明。

8.2.1 GAN架构

VAE利用潜在空间，可以生成连续的新图像，不过因损失函数采用像素间的距离，所以图像有点模糊。能否生成更清晰的新图像呢？可以的，这里我们用GAN替换VAE的潜在空间，它能够迫使生成图像与真实图像在统计上几乎无法区别的逼真合成图像。
GAN的直观理解，可以想象一个名画伪造者想伪造一幅达芬奇的画作，开始时，伪造者技术不精，但他，将自己的一些赝品和达芬奇的作品混在一起，请一个艺术商人对每一幅画进行真实性评估，并向伪造者反馈，告诉他哪些看起来像真迹、哪些看起来不像真迹。
伪造者根据这些反馈，改进自己的赝品。随着时间的推移，伪造者技能越来越高，艺术商人也变得越来越擅长找出赝品。最后，他们手上就拥有了一些非常逼真的赝品。
这就是GAN的基本原理。这里有两个角色，一个是伪造者，另一个是技术鉴赏者。他们训练的目的都是打败对方。
因此，GAN从网络的角度来看，它由两部分组成。
（1）生成器网络：它一个潜在空间的随机向量作为输入，并将其解码为一张合成图像。
（2）判别器网络：以一张图像（真实的或合成的均可）作为输入，并预测该图像来自训练集还是来自生成器网络。图8-6 为其架构图。

图8-6 GAN架构图
如何不断提升判别器辨别是非的能力？如何使生成的图片越来越像真图片？这些都通过控制它们各自的损失函数来控制。
训练结束后，生成器能够将输入空间中的任何点转换为一张可信图像。与VAE不同的是，这个潜空间无法保证带连续性或有特殊含义的结构。
GAN的优化过程不像通常的求损失函数的最小值，而是保持生成与判别两股力量的动态平衡。因此，其训练过程要比一般神经网络难很多。

8.2.2 GAN的损失函数

从GAN的架构图(图8-6)可知，控制生成器或判别器的关键是损失函数，如何定义损失函数成为整个GAN的关键。我们的目标很明确，既要不断提升判断器辨别是非或真假的能力，又要不断提升生成器不断提升图片质量，使判别器越来越难判别。这些目标如何用程序体现？损失函数就能充分说明。
为了达到判别器的目标，其损失函数既要考虑识别真图片能力，又要考虑识别假图片能力，而不能只考虑一方面，故判别器的损失函数为两者的和，具体代码如下：
D表示判别器，G为生成器，real_labels，fake_labels分别表示真图片标签、假图片标签。images是真图片，z是从潜在空间随机采样的向量，通过生成器得到假图片。

# 定义判断器对真图片的损失函数
outputs = D(images)
d_loss_real = criterion(outputs, real_labels)
real_score = outputs
        
# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数
z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)
d_loss_fake = criterion(outputs, fake_labels)
fake_score = outputs            
# 得到判别器总的损失函数
d_loss = d_loss_real + d_loss_fake

# 定义判断器对真图片的损失函数

outputs = D(images)

d_loss_real = criterion(outputs, real_labels)

real_score = outputs

# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

d_loss_fake = criterion(outputs, fake_labels)

fake_score = outputs

# 得到判别器总的损失函数

d_loss = d_loss_real + d_loss_fake

生成器的损失函数如何定义，才能使其越来越向真图片靠近？以真图片为标杆或标签即可。具体代码如下：

z = torch.randn(batch_size, latent_size).to(device)
fake_images = G(z)
outputs = D(fake_images)        
        
g_loss = criterion(outputs, real_labels)

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

g_loss = criterion(outputs, real_labels)

8.3用GAN生成图像

为便于说明GAN的关键环节，这里我们弱化了网络和数据集的复杂度。数据集为MNIST、网络用全连接层。后续我们将用一些卷积层的实例来说明。

8.3.1判别器

获取数据，导入模块基本与AVE的类似，这里就不展开来说，详细内容大家可参考char-08代码模块。
定义判别器网络结构，这里使用LeakyReLU为激活函数，输出一个节点并经过Sigmoid后输出，用于真假二分类。

# 构建判断器
D = nn.Sequential(
    nn.Linear(image_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, hidden_size),
    nn.LeakyReLU(0.2),
    nn.Linear(hidden_size, 1),
    nn.Sigmoid())

# 构建判断器

D = nn.Sequential(

nn.Linear(image_size, hidden_size),

nn.LeakyReLU(0.2),

nn.Linear(hidden_size, hidden_size),

nn.LeakyReLU(0.2),

nn.Linear(hidden_size, 1),

nn.Sigmoid())

8.3.2 生成器

生成器与AVE的生成器类似，不同的地方是输出为nn.tanh,使用nn.tanh将使数据分布在[-1,1]之间。其输入是潜在空间的向量z，输出维度与真图片相同。

# 构建生成器，这个相当于AVE中的解码器 
G = nn.Sequential(
    nn.Linear(latent_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, hidden_size),
    nn.ReLU(),
    nn.Linear(hidden_size, image_size),
    nn.Tanh())

# 构建生成器，这个相当于AVE中的解码器

G = nn.Sequential(

nn.Linear(latent_size, hidden_size),

nn.ReLU(),

nn.Linear(hidden_size, hidden_size),

nn.ReLU(),

nn.Linear(hidden_size, image_size),

nn.Tanh())

8.3.3 训练模型

for epoch in range(num_epochs):
    for i, (images, _) in enumerate(data_loader):
        images = images.reshape(batch_size, -1).to(device)
        
        # 定义图像是真或假的标签
        real_labels = torch.ones(batch_size, 1).to(device)
        fake_labels = torch.zeros(batch_size, 1).to(device)

        # ================================================================== #
        #                      训练判别器                                    #
        # ================================================================== #

        # 定义判别器对真图片的损失函数
        outputs = D(images)
        d_loss_real = criterion(outputs, real_labels)
        real_score = outputs
        
        # 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        d_loss_fake = criterion(outputs, fake_labels)
        fake_score = outputs        
     
        # 得到判别器总的损失函数
        d_loss = d_loss_real + d_loss_fake
        
        # 对生成器、判别器的梯度清零        
        reset_grad()
        d_loss.backward()
        d_optimizer.step()
        
        # ================================================================== #
        #                        训练生成器                                  #
        # ================================================================== #

        # 定义生成器对假图片的损失函数，这里我们要求
        #判别器生成的图片越来越像真图片，故损失函数中
        #的标签改为真图片的标签，即希望生成的假图片，
        #越来越靠近真图片
        z = torch.randn(batch_size, latent_size).to(device)
        fake_images = G(z)
        outputs = D(fake_images)
        
        
        g_loss = criterion(outputs, real_labels)
        
        # 对生成器、判别器的梯度清零
        #进行反向传播及运行生成器的优化器
        reset_grad()
        g_loss.backward()
        g_optimizer.step()
        
        if (i+1) % 200 == 0:
            print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}' 
                  .format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(), 
                          real_score.mean().item(), fake_score.mean().item()))
    
    # 保存真图片
    if (epoch+1) == 1:
        images = images.reshape(images.size(0), 1, 28, 28)
        save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))
    
    # 保存假图片
    fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
    save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))

# 保存模型
torch.save(G.state_dict(), 'G.ckpt')
torch.save(D.state_dict(), 'D.ckpt')

for epoch in range(num_epochs):

for i, (images, _) in enumerate(data_loader):

images = images.reshape(batch_size, -1).to(device)

# 定义图像是真或假的标签

real_labels = torch.ones(batch_size, 1).to(device)

fake_labels = torch.zeros(batch_size, 1).to(device)

# ================================================================== #

# 训练判别器 #

# ================================================================== #

# 定义判别器对真图片的损失函数

outputs = D(images)

d_loss_real = criterion(outputs, real_labels)

real_score = outputs

# 定义判别器对假图片（即由潜在空间点生成的图片）的损失函数

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

d_loss_fake = criterion(outputs, fake_labels)

fake_score = outputs

# 得到判别器总的损失函数

d_loss = d_loss_real + d_loss_fake

# 对生成器、判别器的梯度清零

reset_grad()

d_loss.backward()

d_optimizer.step()

# ================================================================== #

# 训练生成器 #

# ================================================================== #

# 定义生成器对假图片的损失函数，这里我们要求

#判别器生成的图片越来越像真图片，故损失函数中

#的标签改为真图片的标签，即希望生成的假图片，

#越来越靠近真图片

z = torch.randn(batch_size, latent_size).to(device)

fake_images = G(z)

outputs = D(fake_images)

g_loss = criterion(outputs, real_labels)

# 对生成器、判别器的梯度清零

#进行反向传播及运行生成器的优化器

reset_grad()

g_loss.backward()

g_optimizer.step()

if (i+1) % 200 == 0:

print('Epoch [{}/{}], Step [{}/{}], d_loss: {:.4f}, g_loss: {:.4f}, D(x): {:.2f}, D(G(z)): {:.2f}'

.format(epoch, num_epochs, i+1, total_step, d_loss.item(), g_loss.item(),

real_score.mean().item(), fake_score.mean().item()))

# 保存真图片

if (epoch+1) == 1:

images = images.reshape(images.size(0), 1, 28, 28)

save_image(denorm(images), os.path.join(sample_dir, 'real_images.png'))

# 保存假图片

fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)

save_image(denorm(fake_images), os.path.join(sample_dir, 'fake_images-{}.png'.format(epoch+1)))

# 保存模型

torch.save(G.state_dict(), 'G.ckpt')

torch.save(D.state_dict(), 'D.ckpt')

8.3.4 可视化结果

可视化每次由生成器得到假图片，即潜在向量z通过生成器得到的图片。

reconsPath = './gan_samples/fake_images-200.png'
Image = mpimg.imread(reconsPath)
plt.imshow(Image) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

reconsPath = './gan_samples/fake_images-200.png'

Image = mpimg.imread(reconsPath)

plt.imshow(Image) # 显示图片

plt.axis('off') # 不显示坐标轴

plt.show()

图8-7 GAN的新图片
图8-7明显好于图8-5。AVE生成图片主要依据原图片与新图片的交叉熵，而GAN真假图片的交叉熵，同时还兼顾了不断提升判别器和生成器本身的性能上。

8.4 VAE与GAN的异同

VAE适合于学习具有良好结构的潜在空间，潜在空间有比较好的连续性，其中存在一些有特定意义的方向。VAE能够捕捉到图像的结构变化（倾斜角度、圈的位置、形状变化、表情变化等）。这也是VAE的一个好处，它有显式的分布，能够容易地可视化图像的分布，具体如图8-8所示。

图8-8 AVE得到的数据流形分布图
GAN生成的潜在空间可能没有良好结构，但GAN生成的图像一般比VAE的更清晰。

Python技术交流与分享

分享技术平台

月度归档：2019年12月

6.4前馈神经网络

6.4.1神经元结构

6.4.2感知机的局限

6.4.3多层神经网络

6.4.4实例：用TensorFlow实现XOR

6.4.5反向传播算法

1.单个神经元的BP算法

2.多层神经网络的BP算法

6.5 实例：用keras构建深度学习架构

8.1 用变分自编码器生成图像

8.1.1 自编码器

8.1.2变分自编码器

8.1.3用变分自编码器生成图像

8.2 GAN简介

8.2.1 GAN架构

8.2.2 GAN的损失函数

8.3用GAN生成图像

8.3.1判别器

8.3.2 生成器

8.3.3 训练模型

8.3.4 可视化结果

8.4 VAE与GAN的异同