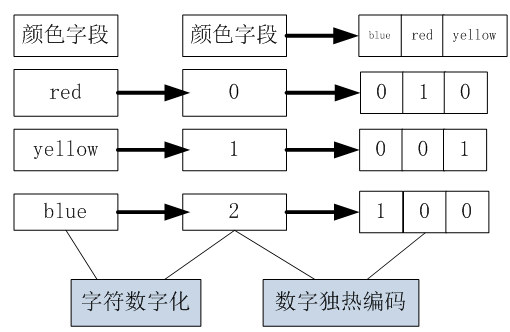
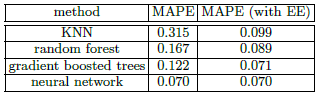
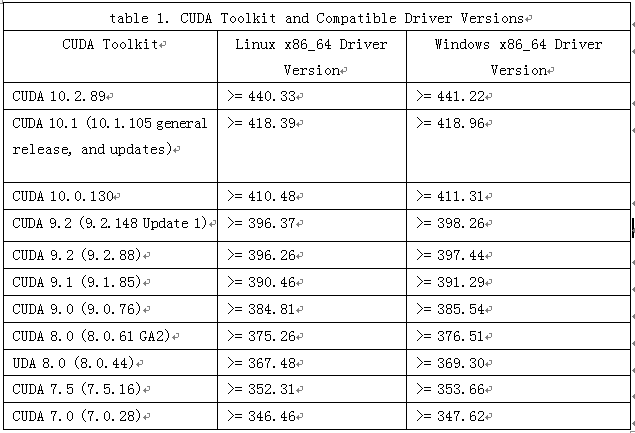
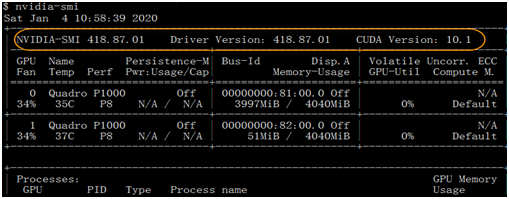
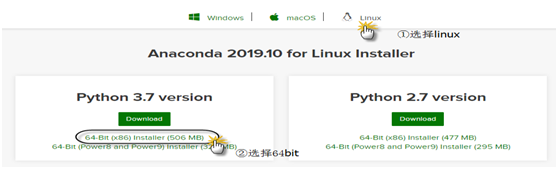
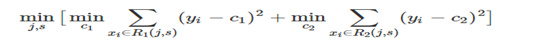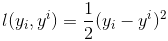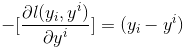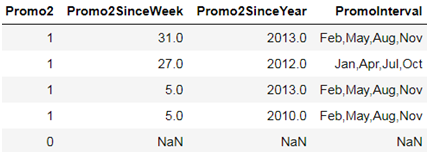在《XGBoost与神经网络谁更牛?》文章,基于相同数据,对XGBoost和神经网络(NN)两种方法进行横行比较。XGBoost是属于Tree Model,只把分类特征进行数字化。对神经网络(NN)先把分类特征数值化,然后转换为One-hot。结果两个算法的测试结果(损失值)如下:
表3-1两种不同算法测试结果

《XGBoost与神经网络谁更牛?》基于相同数据集用不同算法进行比较,本章将从纵向进行比较,即基于相同数据集,相同算法(都是神经网络NN),但特征处理方式不同。一种是《XGBoost与神经网络谁更牛?》的方法,另外一种对分类特征采用Embedding方法,把分类特征转换为向量,并且这些向量的值会随着模型的迭代而自动更新。这两种方法比较的结果如表3-2所示:
表3-2 同一算法不同特征处理方式的测试结果

训练及测试数据没有打乱,其中测试数据是最新原数据的10%。
从表3-2可以看出,使用EE处理分类特征的方法性能远好于不使用EE的神经网络,使用EE有利于充分发挥NN的潜能,提升NN在实现传统机器学习任务的性能。
EE处理方法为何能大大提升模型的性能?使用EE处理特征有哪些优势,Embedding方法是否还适合于处理其它特征?如连续特征、时许特征、图(graph)特征等。这些问题后续将陆续进行说明。接下来我们将用Keras或TensorFlow的Embeding层处理分类特征。
3.1 Embedding简介
神经网络、深度学习的应用越来越广泛,从计算机视觉到自然语言处理和时间序列预测。在这些领域都取得不错成绩,有很多落地项目性能已超过人的平均水平。不但有较好的性能,特征工程方面更是实现了特征工程的自动化。
特征工程是传统机器学习的核心任务,模型性能如何很大程度取决特征工程处理方法,由此,要得到理想的特征工程往往需要很多业务和技术方面的技巧,因此有“特征工程是一门艺术”的说法,这也从一个侧面说明特征工程的门槛比较高,不利于普及和推广。不过这种情况,近些年正在改变。为了解决这一大瓶颈,人们开始使用神经网络或深度学习方法处理传统机器学习任务,特征工程方法使用Embedding 方法,把离散变量转变为较低维的向量,通过这种方式,我们可以将神经网络,深度学习用于更广泛的领域。
目前Embedding已广泛使用在自然语言处理(NLP)、结构化数据、图形数据等处理方面。在NLP 中常用的 Word Embedding ,对结构化数据使用 Entity Embedding,对图形数据采用Graph Embedding。这些内容后续我们将陆续介绍。这里先介绍如何用keras或TensorFlow实现分类特征的Embedding。
3.1.1 Keras.Embedding格式
keras的Embedding层格式如下:
|
1 |
keras.layers.Embedding(input_dim, output_dim, embeddings_initializer='uniform', embeddings_regularizer=None, activity_regularizer=None, embeddings_constraint=None, mask_zero=False, input_length=None) |
Keras提供了一个嵌入层(Embedding layer),可用于处理文本数据、分类数据等的神经网络。它要求输入数据进行整数编码,以便每个单词或类别由唯一的整数表示。嵌入层使用随机权重初始化,并将学习所有数据集中词或类别的表示。这层只能作为模型的第1层。
【参数说明】
input_dim: int > 0。词汇表大小或类别总数, 即,最大整数索引(index) + 1。
output_dim: int >= 0。词向量的维度。
embeddings_initializer: embeddings 矩阵的初始化方法 (详见 https://keras.io/initializers/)。
embeddings_regularizer: embeddings matrix 的正则化方法
(详见https://keras.io/regularizers/)。
embeddings_constraint: embeddings matrix 的约束函数 (详见 https://keras.io/constraints/)。
mask_zero: 是否把 0 看作为一个应该被遮蔽的特殊的 "padding" 值。这对于可变长的循环神经网络层十分有用。 如果设定为 True,那么接下来的所有层都必须支持 masking,否则就会抛出异常。 如果 mask_zero 为 True,作为结果,索引 0 就不能被用于词汇表中 (input_dim 应该与 vocabulary + 1 大小相同)。
input_length: 输入序列的长度,当它是固定的时。 如果你需要连接 Flatten 和 Dense 层,则这个参数是必须的 (没有它,dense 层的输出尺寸就无法计算)。
输入尺寸
尺寸为 (batch_size, sequence_length) 的 2D 张量。
输出尺寸
尺寸为 (batch_size, sequence_length, output_dim) 的 3D 张量。
更多信息可参考官网:
https://keras.io/layers/embeddings/
https://keras.io/zh/layers/embeddings/(中文)
假设定义一个词汇量为200的嵌入层的整数编码单词,将词嵌入到32维的向量空间,每次输入50个单词的输入文档,那么对应的embedding可写成如下格式:
|
1 |
em=Embedding(200,32,input_length=50) |
为更好理解Keras的Embedding层的使用,下面列举几个具体实例。
(1)简单实例代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
model = Sequential() model.add(Embedding(1000, 64, input_length=10)) # 模型将输入一个大小为 (batch, input_length) 的整数矩阵。 # 输入中最大的整数(即词索引)不应该大于 999 (词汇表大小) #生成输入矩阵,batch=32,input_length=10 input_array = np.random.randint(1000, size=(32, 10)) #编译模型 model.compile('rmsprop', 'mse') #进行预测 output_array = model.predict(input_array) # 现在 model.output_shape == (None, 10, 64),其中 None 是 batch 的维度。 print(output_array.shape) ###(32, 10, 64) |
(2)用Embedding学习文本表示实例
假设有10个文本文档,每个文档都有一个学生提交的工作评论。每个文本文档被分类为正的“1”或负的“0”。这是一个简单的情感分析问题。用Keras的Embedding学习这10个文本的表示,具体实现代码如下;
#导入需要的模块
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
import numpy as np from tensorflow.keras.preprocessing.text import one_hot from tensorflow.keras.preprocessing.sequence import pad_sequences from tensorflow.keras.models import Sequential from tensorflow.keras.layers import Dense from tensorflow.keras.layers import Flatten from tensorflow.keras.layers import Embedding #定义一个文档,这个文档有10句语句 docs = ['Well done!', 'Good work', 'Great effort', 'nice work', 'Excellent!', 'Weak', 'Poor effort!', 'not good', 'poor work', 'Could have done better.'] #定义对应的类标签 labels = np.array([1,1,1,1,1,0,0,0,0,0]) vocab_size = 50 # 用one-hot函数将文本编码为大小为vocab_size的单词索引列表 encoded_docs = [one_hot(d, vocab_size) for d in docs] print("把文本转换为整数") print(encoded_docs) # 将序列填充到相同的长度(长度为4) max_length = 4 padded_docs = pad_sequences(encoded_docs, maxlen=max_length, padding='post') print("填充向量") print(padded_docs) #定义模型 model = Sequential() model.add(Embedding(vocab_size,8,input_length=max_length,name='word_embedding')) model.add(Flatten()) model.add(Dense(1, activation='sigmoid')) #编译模型 model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['acc']) #查看模型结构 print("查看模型结构") print(model.summary()) #拟合模型 model.fit(padded_docs, labels, epochs=50, verbose=0) #评估模型 loss, accuracy = model.evaluate(padded_docs, labels, verbose=0) print("查看模型精度") print('Accuracy: %f' % (accuracy*100)) |
运行结果如下:
把文本转换为整数
[[49, 28], [33, 36], [21, 41], [18, 36], [32], [29], [18, 41], [30, 33], [18, 36], [43, 17, 28, 34]]
填充向量
[[49 28 0 0]
[33 36 0 0]
[21 41 0 0]
[18 36 0 0]
[32 0 0 0]
[29 0 0 0]
[18 41 0 0]
[30 33 0 0]
[18 36 0 0]
[43 17 28 34]]
查看模型结构
Model: "sequential_5"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding_5 (Embedding) (None, 4, 8) 400
_________________________________________________________________
flatten_4 (Flatten) (None, 32) 0
_________________________________________________________________
dense_4 (Dense) (None, 1) 33
=================================================================
Total params: 433
Trainable params: 433
Non-trainable params: 0
_________________________________________________________________
None
查看模型精度
Accuracy: 89.999998
查看通过50次迭代后的Embedding矩阵。
|
1 2 |
model.get_layer('word_embedding').get_weights()[0].shape ##(50,8) model.get_layer('word_embedding').get_weights()[0][:3] #查看前3行 |
运行结果如下:
array([[ 0.03469506, 0.05556902, -0.06460979, 0.04944995, -0.04956526,
-0.01446372, -0.01657126, 0.04287368],
[ 0.04969586, -0.0284451 , -0.03200825, -0.00149088, 0.04212971,
-0.00741715, -0.02147427, -0.02345204],
[ 0.00152697, 0.04381416, 0.01856637, -0.00952369, 0.04007444,
0.00964203, -0.0313913 , -0.04820969]], dtype=float32)
3.1.2 Dense简介
|
1 |
keras.layers.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None) |
Dense就是常用的的全连接层,它实现以下操作:
|
1 |
output = activation(dot(input, kernel) + bias) |
其中 activation 是按逐个元素计算的激活函数,kernel 是由网络层创建的权值矩阵,以及 bias 是其创建的偏置向量 (只在 use_bias 为 True 时才有用)。
注意: 如果该层的输入的秩大于2,那么它首先被展平然后 再计算与 kernel 的点乘。
【参数说明】
units: 正整数,输出空间维度。
activation: 激活函数 (详见 activations)。 若不指定,则不使用激活函数 (即,「线性」激活: a(x) = x)。
use_bias: 布尔值,该层是否使用偏置向量。
kernel_initializer: kernel 权值矩阵的初始化器 (详见https://keras.io/zh/initializers/)。
bias_initializer: 偏置向量的初始化器 (详见https://keras.io/zh/initializers/).
kernel_regularizer: 运用到 kernel 权值矩阵的正则化函数 (详见 https://keras.io/zh/regularizers/)。
bias_regularizer: 运用到偏置向的的正则化函数 (详见 https://keras.io/zh/regularizers/)。
activity_regularizer: 运用到层的输出的正则化函数 (它的 "activation")。 (详见 https://keras.io/zh/regularizers/)。
kernel_constraint: 运用到 kernel 权值矩阵的约束函数 (详见https://keras.io/zh/constraints/)。
bias_constraint: 运用到偏置向量的约束函数 (详见https://keras.io/zh/constraints/)。
输入尺寸
nD张量,尺寸: (batch_size, ..., input_dim)。 最常见的情况是一个尺寸为 (batch_size, input_dim) 的2D输入。
输出尺寸
nD张量,尺寸: (batch_size, ..., units)。 例如,对于尺寸为 (batch_size, input_dim)的2D输入, 输出的尺寸为 (batch_size, units)。
简单示例代码:
|
1 2 3 4 5 6 7 8 |
# 作为 Sequential 模型的第一层 model = Sequential() model.add(Dense(32, input_shape=(16,))) # 现在模型就会以尺寸为 (*, 16) 的数组作为输入, # 其输出数组的尺寸为 (*, 32) # 在第一层之后,就不再需要指定输入的尺寸了: model.add(Dense(32)) |
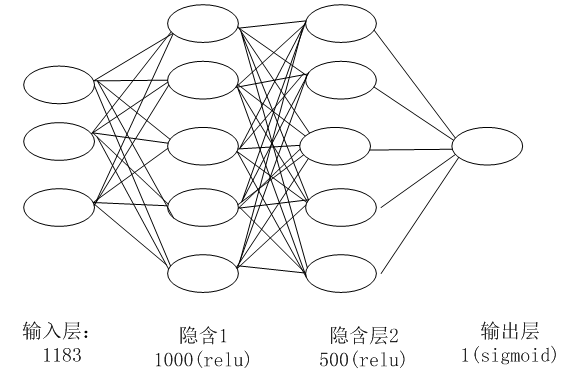
3.2 NN架构
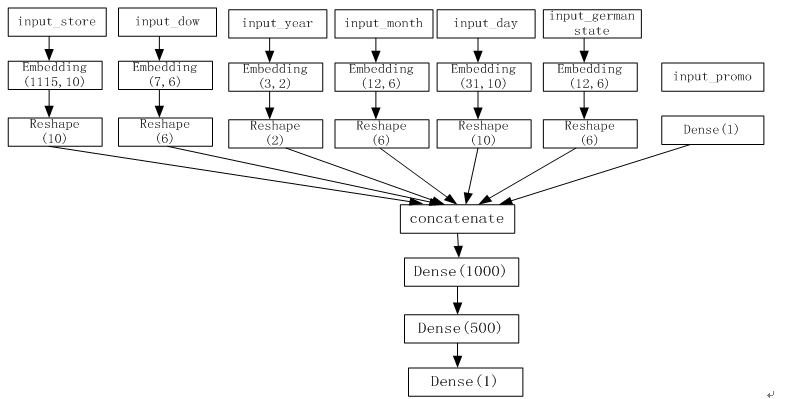
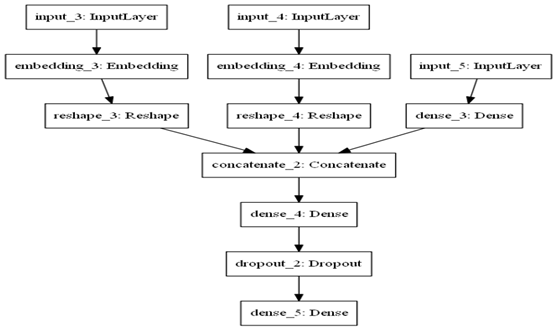
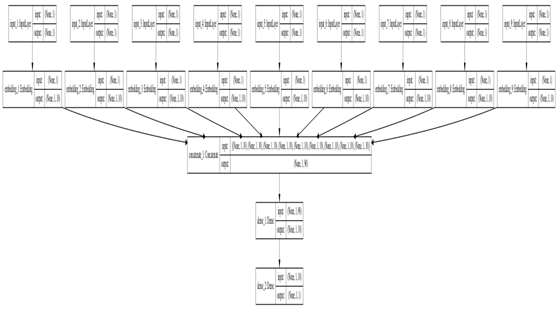
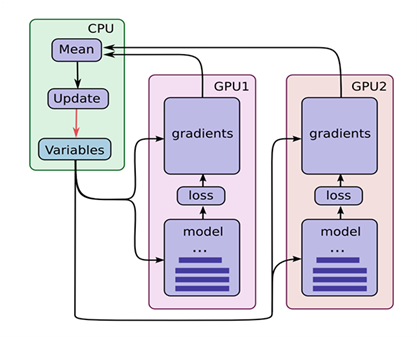
图3-1 NN架构图
从图3-1可知,NN共处理7个特征,其中promo特征因只有2个值(0或1),无需转换为Embedding向量,其它6个特征,根据类别数,分别做了Embedding处理。处理后合并这7个特征,再通过3个全连接层。
3.3 分类特征处理
基于第2章(《XGBoost与NN谁更牛?》)处理保存的feature_train_data.pickle文件,做如下处理:
3.3.1 数据预处理
(1)定义对特征进行Embedding处理函数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
#从训练结果读取各特征的embedding向量,并用这些向量作为输入值 def embed_features(X, saved_embeddings_fname): # f_embeddings = open("embeddings_shuffled.pickle", "rb") f_embeddings = open(saved_embeddings_fname, "rb") embeddings = pickle.load(f_embeddings) #因store_open,promo这两列(索引分别为0、3),至多只有两个值,没有进行embedding,故需排除在外 index_embedding_mapping = {1: 0, 2: 1, 4: 2, 5: 3, 6: 4, 7: 5} X_embedded = [] (num_records, num_features) = X.shape for record in X: embedded_features = [] for i, feat in enumerate(record): feat = int(feat) if i not in index_embedding_mapping.keys(): embedded_features += [feat] else: embedding_index = index_embedding_mapping[i] embedded_features += embeddings[embedding_index][feat].tolist() X_embedded.append(embedded_features) return numpy.array(X_embedded) #分别取出各特征,因第1列只有1个值,不用第1列(即索引为0的列) def split_features(X): X_list = [] #获取X第2列数据 store_index = X[..., [1]] X_list.append(store_index) #获取X第3列数据,以下类推 day_of_week = X[..., [2]] X_list.append(day_of_week) promo = X[..., [3]] X_list.append(promo) year = X[..., [4]] X_list.append(year) month = X[..., [5]] X_list.append(month) day = X[..., [6]] X_list.append(day) State = X[..., [7]] X_list.append(State) return X_list |
(2)导入模块
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import pickle import numpy numpy.random.seed(123) from tensorflow.keras.models import Sequential from tensorflow.keras.models import Model as KerasModel from tensorflow.keras.layers import Input, Dense, Activation, Reshape,Flatten from tensorflow.keras.layers import Concatenate from tensorflow.keras.layers import Embedding from tensorflow.keras.callbacks import ModelCheckpoint import sys sys.setrecursionlimit(10000) train_ratio = 0.9 shuffle_data = False one_hot_as_input = False embeddings_as_input = False save_embeddings = True saved_embeddings_fname = "embeddings.pickle" # set save_embeddings to True to create this file |
(3)读取数据
|
1 2 3 4 5 |
f = open('feature_train_data.pickle', 'rb') (X, y) = pickle.load(f) num_records = len(X) train_size = int(train_ratio * num_records) |
(4)生成训练、测试数据
|
1 2 3 4 |
X_train = X[:train_size] X_val = X[train_size:] y_train = y[:train_size] y_val = y[train_size:] |
(5)定义采样函数
|
1 2 3 4 5 |
def sample(X, y, n): '''random samples''' num_row = X.shape[0] indices = numpy.random.randint(num_row, size=n) return X[indices, :], y[indices] |
(6)采样生成训练数据
|
1 2 |
X_train, y_train = sample(X_train, y_train, 200000) # Simulate data sparsity print("Number of samples used for training: " + str(y_train.shape[0])) |
3.3.2 构建模型
(1)定义Model类
|
1 2 3 4 5 6 7 8 |
class Model(object): def evaluate(self, X_val, y_val): assert(min(y_val) > 0) guessed_sales = self.guess(X_val) relative_err = numpy.absolute((y_val - guessed_sales) / y_val) result = numpy.sum(relative_err) / len(y_val) return result |
(2)构建模型
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
class NN_with_EntityEmbedding(Model): def __init__(self, X_train, y_train, X_val, y_val): super().__init__() self.epochs = 10 self.checkpointer = ModelCheckpoint(filepath="best_model_weights.hdf5", verbose=1, save_best_only=True) self.max_log_y = max(numpy.max(numpy.log(y_train)), numpy.max(numpy.log(y_val))) self.__build_keras_model() self.fit(X_train, y_train, X_val, y_val) def preprocessing(self, X): X_list = split_features(X) return X_list def __build_keras_model(self): input_store = Input(shape=(1,)) output_store = Embedding(1115, 10, name='store_embedding')(input_store) output_store = Reshape(target_shape=(10,))(output_store) input_dow = Input(shape=(1,)) output_dow = Embedding(7, 6, name='dow_embedding')(input_dow) output_dow = Reshape(target_shape=(6,))(output_dow) #promo只有0、1两个值,无需进行Embedding input_promo = Input(shape=(1,)) output_promo = Dense(1)(input_promo) input_year = Input(shape=(1,)) output_year = Embedding(3, 2, name='year_embedding')(input_year) output_year = Reshape(target_shape=(2,))(output_year) input_month = Input(shape=(1,)) output_month = Embedding(12, 6, name='month_embedding')(input_month) output_month = Reshape(target_shape=(6,))(output_month) input_day = Input(shape=(1,)) output_day = Embedding(31, 10, name='day_embedding')(input_day) output_day = Reshape(target_shape=(10,))(output_day) input_germanstate = Input(shape=(1,)) output_germanstate = Embedding(12, 6, name='state_embedding')(input_germanstate) output_germanstate = Reshape(target_shape=(6,))(output_germanstate) input_model = [input_store, input_dow, input_promo, input_year, input_month, input_day, input_germanstate] output_embeddings = [output_store, output_dow, output_promo, output_year, output_month, output_day, output_germanstate] output_model = Concatenate()(output_embeddings) output_model = Dense(1000, kernel_initializer="uniform")(output_model) output_model = Activation('relu')(output_model) output_model = Dense(500, kernel_initializer="uniform")(output_model) output_model = Activation('relu')(output_model) output_model = Dense(1)(output_model) output_model = Activation('sigmoid')(output_model) self.model = KerasModel(inputs=input_model, outputs=output_model) self.model.compile(loss='mean_absolute_error', optimizer='adam') def _val_for_fit(self, val): val = numpy.log(val) / self.max_log_y return val def _val_for_pred(self, val): return numpy.exp(val * self.max_log_y) def fit(self, X_train, y_train, X_val, y_val): self.model.fit(self.preprocessing(X_train), self._val_for_fit(y_train), validation_data=(self.preprocessing(X_val), self._val_for_fit(y_val)), epochs=self.epochs, batch_size=128, # callbacks=[self.checkpointer], ) # self.model.load_weights('best_model_weights.hdf5') print("Result on validation data: ", self.evaluate(X_val, y_val)) def guess(self, features): features = self.preprocessing(features) result = self.model.predict(features).flatten() return self._val_for_pred(result) |
(3)训练模型
|
1 2 3 4 5 |
models = [] print("Fitting NN_with_EntityEmbedding...") for i in range(5): models.append(NN_with_EntityEmbedding(X_train, y_train, X_val, y_val)) |
运行部分结果
Fitting NN_with_EntityEmbedding...
Train on 200000 samples, validate on 84434 samples
Epoch 1/10
200000/200000 [==============================] - 37s 185us/sample - loss: 0.0140 - val_loss: 0.0113
Epoch 2/10
200000/200000 [==============================] - 33s 165us/sample - loss: 0.0093 - val_loss: 0.0110
Epoch 3/10
200000/200000 [==============================] - 34s 168us/sample - loss: 0.0085 - val_loss: 0.0104
Epoch 4/10
200000/200000 [==============================] - 35s 173us/sample - loss: 0.0079 - val_loss: 0.0107
Epoch 5/10
200000/200000 [==============================] - 37s 184us/sample - loss: 0.0076 - val_loss: 0.0100
Epoch 6/10
200000/200000 [==============================] - 38s 191us/sample - loss: 0.0074 - val_loss: 0.0095
Epoch 7/10
200000/200000 [==============================] - 31s 154us/sample - loss: 0.0072 - val_loss: 0.0097
Epoch 8/10
200000/200000 [==============================] - 33s 167us/sample - loss: 0.0071 - val_loss: 0.0091
Epoch 9/10
200000/200000 [==============================] - 36s 181us/sample - loss: 0.0069 - val_loss: 0.0090
Epoch 10/10
200000/200000 [==============================] - 40s 201us/sample - loss: 0.0068 - val_loss: 0.0089
Result on validation data: 0.09481584162850512
Train on 200000 samples, validate on 84434 samples
Epoch 1/10
200000/200000 [==============================] - 38s 191us/sample - loss: 0.0143 - val_loss: 0.0125
Epoch 2/10
200000/200000 [==============================] - 41s 206us/sample - loss: 0.0096 - val_loss: 0.0107
Epoch 3/10
200000/200000 [==============================] - 46s 232us/sample - loss: 0.0089 - val_loss: 0.0105
Epoch 4/10
200000/200000 [==============================] - 39s 197us/sample - loss: 0.0082 - val_loss: 0.0099
Epoch 5/10
200000/200000 [==============================] - 39s 197us/sample - loss: 0.0077 - val_loss: 0.0095
Epoch 6/10
200000/200000 [==============================] - 41s 207us/sample - loss: 0.0075 - val_loss: 0.0111
Epoch 7/10
200000/200000 [==============================] - 39s 193us/sample - loss: 0.0073 - val_loss: 0.0092
Epoch 8/10
200000/200000 [==============================] - 50s 248us/sample - loss: 0.0071 - val_loss: 0.0092
Epoch 9/10
200000/200000 [==============================] - 46s 228us/sample - loss: 0.0070 - val_loss: 0.0094
Epoch 10/10
200000/200000 [==============================] - 44s 221us/sample - loss: 0.0069 - val_loss: 0.0091
Result on validation data: 0.09585602861091462
3.3.3 验证模型
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
#求多个模型的集成精度 def evaluate_models(models, X, y): assert(min(y) > 0) guessed_sales = numpy.array([model.guess(X) for model in models]) mean_sales = guessed_sales.mean(axis=0) relative_err = numpy.absolute((y - mean_sales) / y) result = numpy.sum(relative_err) / len(y) return result print("Evaluate combined models...") print("Training error...") r_train = evaluate_models(models, X_train, y_train) print(r_train) print("Validation error...") r_val = evaluate_models(models, X_val, y_val) print(r_val) |
运行结果如下:
Evaluate combined models...
Training error...
0.06760082089742254
Validation error...
0.09348419043167332
3.4 可视化Entity Embedding
把特征转换为Entity Embedding之后,可以利用t-SNE进行可视化,如对store特征的Embedding降维后进行可视化,从可视化结果揭示出一些重要信息,彼此相似的类别比较接近。
3.4.1 保存Embedding
|
1 2 3 4 5 6 7 8 9 10 11 12 |
#保存各特征的embedding值 if save_embeddings: model = models[3].model store_embedding = model.get_layer('store_embedding').get_weights()[0] dow_embedding = model.get_layer('dow_embedding').get_weights()[0] year_embedding = model.get_layer('year_embedding').get_weights()[0] month_embedding = model.get_layer('month_embedding').get_weights()[0] day_embedding = model.get_layer('day_embedding').get_weights()[0] german_states_embedding = model.get_layer('state_embedding').get_weights()[0] with open(saved_embeddings_fname, 'wb') as f: pickle.dump([store_embedding, dow_embedding, year_embedding, month_embedding, day_embedding, german_states_embedding], f, -1) |
3.4.2 可视化Embedding特征
(1)导入模块
|
1 2 3 4 5 6 7 8 9 10 |
import pickle from sklearn import manifold import matplotlib.pyplot as plt import numpy as np %matplotlib inline #屏蔽警告信息 import warnings warnings.filterwarnings('ignore') |
(2)读取保存的embedding文件
|
1 2 3 |
with open("embeddings.pickle", 'rb') as f: [store_embedding, dow_embedding, year_embedding, month_embedding, day_embedding, german_states_embedding] = pickle.load(f) |
(3)定义对应各州的名称
|
1 |
states_names = ["柏林","巴登•符腾堡","拜仁","下萨克森","黑森","汉堡","北莱茵•威斯特法伦州","莱茵兰•普法尔茨州","石勒苏益格荷尔斯泰因州","萨克森州","萨克森安哈尔特州","图林根州"] |
(4)可视化german_states_embedding
|
1 2 3 4 5 6 7 8 9 |
plt.rcParams['font.sans-serif']=['SimHei'] ##显示中文 plt.rcParams['axes.unicode_minus']=False ##防止坐标轴上的-号变为方块 tsne = manifold.TSNE(init='pca', random_state=0, method='exact') Y = tsne.fit_transform(german_states_embedding) plt.figure(figsize=(8,8)) plt.scatter(-Y[:, 0], -Y[:, 1]) for i, txt in enumerate(states_names): plt.annotate(txt, (-Y[i, 0],-Y[i, 1]), xytext = (-20, 8), textcoords = 'offset points') plt.savefig('state_embedding.pdf') |
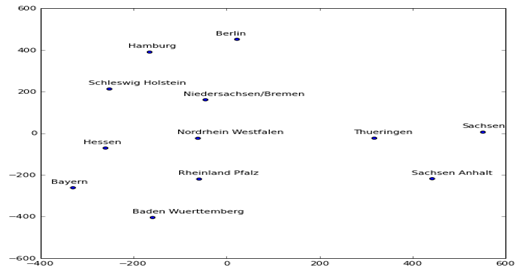
可视化结果如下:

图3-2 可视化german_states_embedding
从图3-2 可知,德国的原属于东德的几个州:萨克森州、萨克森安哈尔特州、图林根州彼此比较接近。其它各州也有类似属性,这就是Embedding通过多次迭代,从数据中学习到一些规则。