循环神经网络语言模型 | Python技术交流与分享

文章目录

3.2 循环神经网络语言模型
3.2.1 RNN结构
3.2.2 RNNCell代码实现
3.2.3 多层RNNCell
3.2.4 多层RNNCell的PyTorch代码实现

3.2 循环神经网络语言模型

神经网络语言模型（NNLM）对统计语言模型而言（如n-gram），前进了一大步。它用词嵌入代替词索引，把词映射到低维向量，用神经网络计算代替词组的统计频率计算，从而有效避免维度灾难、增强了词的表现力和模型的泛化力。不过NNLM除计算效率问题外，主要还是基于n-gram的思想，虽然对n有所扩充，但是本质上仍然是使用神经网络编码的n-gram模型，而且对输入数据要求固定长度(一般取5-10)，这严重影响模型的性能和泛化能力，所以，如何打破n的"桎梏"一直是人们追求的方向。
循环神经网络(RNN)（尤其其改进版本LSTM）序列语言模型的提出，较好的解决了如何学习到长距离的依赖关系的问题，接下来将从多个角度、多个层次详细介绍RNN。

3.2.1 RNN结构

图1-8是循环神经网络的经典结构，从图中可以看到输入x、隐含层、输出层等，这些与传统神经网络类似，不过自循环W却是它的一大特色。这个自循环直观理解就是神经元之间还有关联，这是传统神经网络、卷积神经网络所没有的。

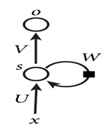
图1-8 循环神经网络的结构
其中U是输入到隐含层的权重矩阵，W是状态到隐含层的权重矩阵，s为状态，V是隐含层到输出层的权重矩阵。图1-8比较抽象，将它展开成图1-9，就更好理解。

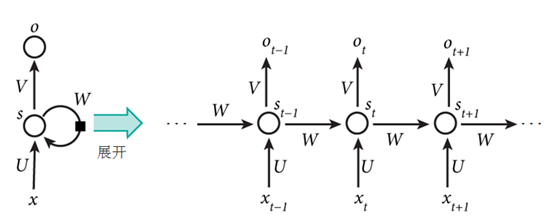
图1-9循环神经网络的展开结构
这是一个典型的Elman循环神经网络，从图7-2不难看出，它的共享参数方式是各个时间节点对应的W、U、V都是不变的，这个机制就像卷积神经网络的过滤器机制一样，通过这种方法实现参数共享，同时大大降低参数量。
图1-9中隐含层不够详细，把隐含层再细化就可得图1-10。

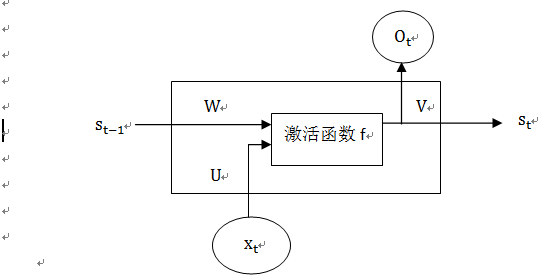
图1-10 循环神经网络Cell的结构图
这个网络在每一时间t有相同的网络结构，假设输入x为n维向量，隐含层的神经元个数为m，输出层的神经元个数为r，则U的大小为n×m维；W是上一次的s_(t-1)作为这一次输入的权重矩阵，大小为m×m维；V是连输出层的权重矩阵，大小为m×r维。而x_t、s_t 和o_t 都是向量，它们各自表示的含义如下：
x_t是时刻t的输入；
s_t是时刻t的隐层状态。它是网络的记忆。s_t基于前一时刻的隐层状态和当前时刻的输入进行计算，
函数f通常是非线性的，如tanh或者ReLU。s_(t-1)为前一个时刻的隐藏状态，其初始化通常为0；
o_t是时刻t的输出。例如，如想预测句子的下一个词，它将会是一个词汇表中的概率向量，o_t=softmax(Vs_t)；
s_t认为是网络的记忆状态，s_t可以捕获之前所有时刻发生的信息。输出o_t的计算仅仅依赖于时刻t的记忆。
图1-10是RNN Cell的结构图，我们可以放大这个图，看看其内部结构，如图1-11所示。

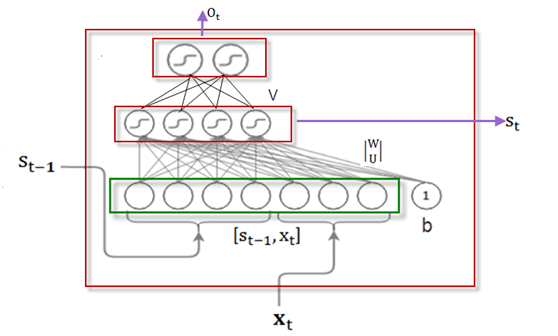
图1-11 RNN 的Cell的内部结构
在图1-11中，把隐含状态s_(t-1) （假设为一个4维向量）
和输入x_t（假设为一个3维向量）拼接成一个7维向量，这个7维向量构成全连接神经网络的输入层，输出为4个节点的向量，激活函数为f，输入与输出间的权重矩阵的维度为[7,4]。这样式（1.6）可写成如下形式：

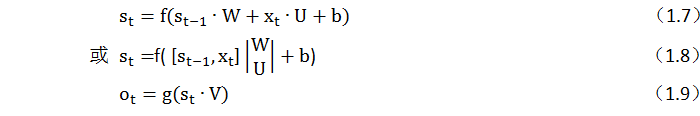
3.2.2 RNNCell代码实现

这里用Python实现（1.8)、（1.9）式，为简便起见，这里不考虑偏移量b。
1、定义激活函数

import numpy as np
#定义sigmoid激活函数
def sigmoid(x):
    return 1/(1+np.exp(-x))

#定义softmax激活函数
def softmax(x):
    # 计算每列的最大值
    column_max = np.max(x)
 
    # 每列元素都需要减去对应的最大值，否则求exp(x)易导致溢出
    exp_x=np.exp(x - column_max)
   
    # 计算softmax
    sum_x = np.sum(exp_x)
    s = exp_x /sum_x
    return s

#创建s及x
x_t,st_1 = np.random.random((1, 3)), np.random.random((1, 4))
#创建权重矩阵
U,W,V = np.random.random((3, 4)), np.random.random((4, 4)),np.random.random((4, 2))

import numpy as np

#定义sigmoid激活函数

def sigmoid(x):

return 1/(1+np.exp(-x))

#定义softmax激活函数

def softmax(x):

# 计算每列的最大值

column_max = np.max(x)

# 每列元素都需要减去对应的最大值，否则求exp(x)易导致溢出

exp_x=np.exp(x - column_max)

# 计算softmax

sum_x = np.sum(exp_x)

s = exp_x /sum_x

return s

#创建s及x

x_t,st_1 = np.random.random((1, 3)), np.random.random((1, 4))

#创建权重矩阵

U,W,V = np.random.random((3, 4)), np.random.random((4, 4)),np.random.random((4, 2))

2、定义状态及输入值，并进行拼接。

#创建s及x
x_t,st_1 = np.random.random((1, 3)), np.random.random((1, 4))
#创建权重矩阵
#创建权重矩阵
U,W,V = np.random.random((3, 4)), np.random.random((4, 4)),np.random.random((4, 2))

#拼接x_t和st_1
xs=np.concatenate((x_t,st_1),axis=1)
#拼接矩阵W和U
WU=np.concatenate((W,U),axis=0)

#创建s及x

x_t,st_1 = np.random.random((1, 3)), np.random.random((1, 4))

#创建权重矩阵

U,W,V = np.random.random((3, 4)), np.random.random((4, 4)),np.random.random((4, 2))

#拼接x_t和st_1

xs=np.concatenate((x_t,st_1),axis=1)

#拼接矩阵W和U

WU=np.concatenate((W,U),axis=0)

3、计算输出值

#计算隐含层的输出值
s_t=sigmoid(np.dot(xs, WU))
#计算输出值
o_t=softmax(np.dot(s_t,V))

#计算隐含层的输出值

s_t=sigmoid(np.dot(xs, WU))

#计算输出值

o_t=softmax(np.dot(s_t,V))

3.2.3 多层RNNCell

上节我们介绍了单个RNN的结构（即RNNCell），有了这个基础之后，我们就可对RNNCell进行拓展。RNN可以横向拓展（增加时间步或序列长度），也可纵向拓展成多层循环神经网络，如图1-12所示。

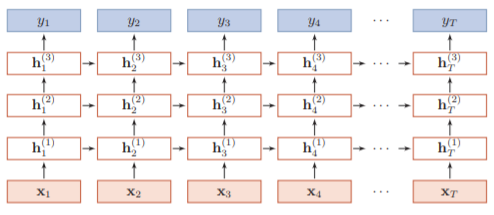
图1-12多层循环神经网络
图1-12中，序列长度为T，网络层数为3。接下来为帮助大家更好的理解，接下来我们用PyTorch实现一个2层RNN。

3.2.4 多层RNNCell的PyTorch代码实现

Pytorch提供了两个版本的循环神经网络接口，单元版的输入是每个时间步，或循环神经网络的一个循环，而封装版的是一个序列。下面我们从简单的封装版torch.nn.RNN开始,其一般格式为：

torch.nn.RNN( args, * kwargs)

1	torch.nn.RNN( args, * kwargs)

由图7-3 可知，RNN状态输出a_t的计算公式为：

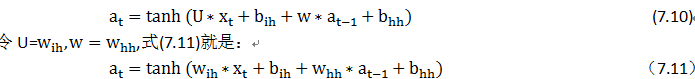
nn.RNN函数中的参数说明如下：
input_size : 输入x的特征数量。
hidden_size : 隐含层的特征数量。
num_layers : RNN的层数。
nonlinearity : 指定非线性函数使用tanh还是relu。默认是tanh。
bias : 如果是False，那么RNN层就不会使用偏置权重 b_i和b_h,默认是True
batch_first : 如果True的话，那么输入Tensor的shape应该是(batch, seq, feature),输出也是这样。默认网络输入是(seq, batch, feature),即序列长度、批次大小、特征维度。
dropout : 如果值非零（该参数取值范围为0~1之间），那么除了最后一层外，其它层的输出都会加上一个dropout层，缺省为零。
bidirectional : 如果True，将会变成一个双向RNN，默认为False。

函数nn.RNN()的输入包括特征及隐含状态，记为(x_t 、h_0),输出包括输出特征及输出隐含状态，记为(output_t 、h_n)。
其中特征值x_t的形状为(seq_len, batch, input_size), h_0的形状为(num_layers * num_directions, batch, hidden_size)，其中num_layers为层数，num_directions方向数，如果取2表示双向(bidirectional,)，取1表示单向。
output_t的形状为(seq_len, batch, num_directions * hidden_size), h_n的形状为(num_layers * num_directions, batch, hidden_size)。
为使大家对循环神经网络有个直观理解，下面先用Pytorch实现简单循环神经网络，然后验证其关键要素。
首先建立一个简单循环神经网络，输入维度为10，隐含状态维度为20，单向两层网络。

rnn = nn.RNN(input_size=10, hidden_size=20,num_layers= 2)

1	rnn = nn.RNN(input_size=10, hidden_size=20,num_layers= 2)

因输入节点与隐含层节点是全连接，根据输入维度、隐含层维度，可以推算出相关权重参数的维度，w_ih应该是20x10，w_hh是20x20, b_ih和b_hh都是hidden_size。以下我们通过查询weight_ih_l0、weight_hh_l0等进行验证。

#第一层相关权重参数形状
print("wih形状{},whh形状{},bih形状{}".format(rnn.weight_ih_l0.shape,rnn.weight_hh_l0.shape,rnn.bias_hh_l0.shape))
#ih形状torch.Size([20, 10]),whh形状torch.Size([20, 20]),bih形状#torch.Size([20])
#第二层相关权重参数形状
print("wih形状{},whh形状{},bih形状{}".format(rnn.weight_ih_l1.shape,rnn.weight_hh_l1.shape,rnn.bias_hh_l1.shape))
# wih形状torch.Size([20, 20]),whh形状torch.Size([20, 20]),bih形状#torch.Size([20])

#第一层相关权重参数形状

print("wih形状{},whh形状{},bih形状{}".format(rnn.weight_ih_l0.shape,rnn.weight_hh_l0.shape,rnn.bias_hh_l0.shape))

#ih形状torch.Size([20, 10]),whh形状torch.Size([20, 20]),bih形状#torch.Size([20])

#第二层相关权重参数形状

print("wih形状{},whh形状{},bih形状{}".format(rnn.weight_ih_l1.shape,rnn.weight_hh_l1.shape,rnn.bias_hh_l1.shape))

# wih形状torch.Size([20, 20]),whh形状torch.Size([20, 20]),bih形状#torch.Size([20])

RNN网络已搭建好，接下来将输入(x_t 、h_0)传入网络，根据网络配置及网络要求，我们生成输入数据。输入特征长度为100，批量大小为32，特征维度为10的张量。隐含状态按网络要求，其形状为(2,32,20)。

#生成输入数据
input=torch.randn(100,32,10)
h_0=torch.randn(2,32,20)

#生成输入数据

input=torch.randn(100,32,10)

h_0=torch.randn(2,32,20)

将输入数据传入RNN网络,将得到输出及更新后隐含状态值。根据以上规则，输出output的形状应该是（100,32,20），隐含状态的输出形状应该与输入的形状一致。

output,h_n=rnn(input,h_0)
print(output.shape,h_n.shape)
#torch.Size([100, 32, 20]) torch.Size([2, 32, 20])

output,h_n=rnn(input,h_0)

print(output.shape,h_n.shape)

#torch.Size([100, 32, 20]) torch.Size([2, 32, 20])

其结果与我们设想的完全一致。