1.自注意力(Self-Attention)
Transformer凭借其自注意力机制,有效解决了字符之间或像素之间的长距离依赖,日益称为NLP和CV领域的通用架构。
自注意力机制是Transformer的核心,如何简洁有效实现Self-Attention?这里介绍一种法,使用einops和PyTorch中einsum。自注意力的计算公式如下
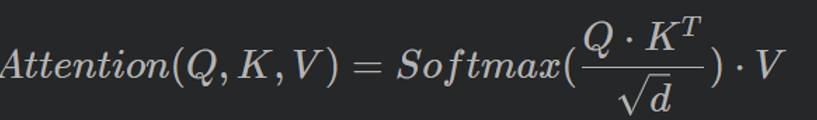
2.自注意力计算的详细过程如下图所示
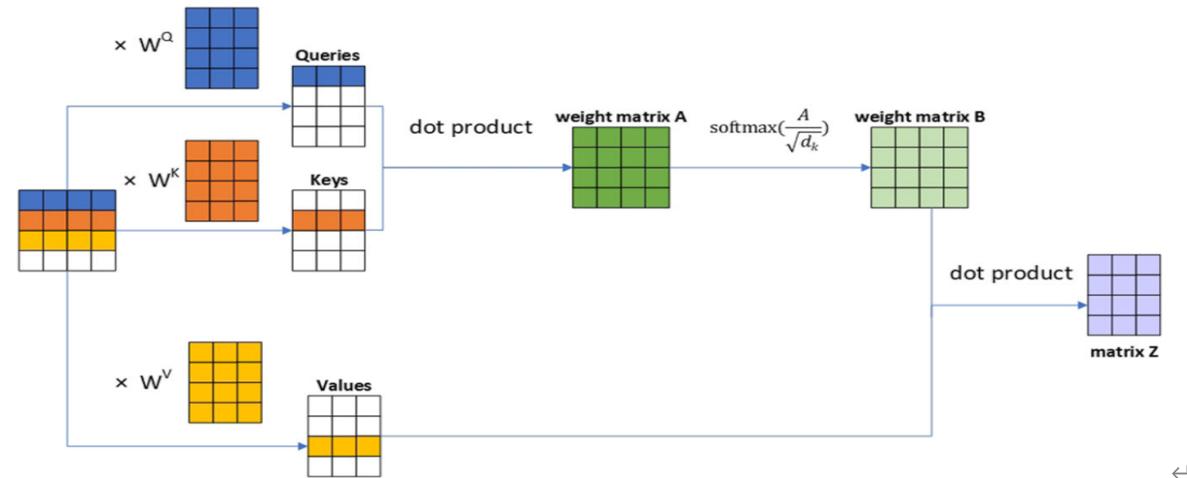
这里假设x的形状(1,4,4),标记(Token)个数为4,每个token转换为长度为4的向量,嵌入(Embedding)的维度为3(dim=3)。
3、详细实现代码
用代码实现上述计算过程
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import numpy as np import torch from einops import rearrange from torch import nn class SelfAttentionAISummer(nn.Module): """ 使用einsum生成自注意力 """ def __init__(self, dim): """ 参数说明: dim: 嵌入向量(embedding vector)维度 输入x假设为3D向量(如b,h,w) """ super().__init__() # 利用全连接层生成Q,K,V这3个4x3矩阵 self.to_qvk = nn.Linear(4, dim * 3, bias=False) # 得到dim(即d)的根号的倒数值 self.scale_factor = dim ** -0.5 # 1/np.sqrt(dim) def forward(self, x, mask=None): assert x.dim() == 3, '3D tensor must be provided' # 生成qkv qkv = self.to_qvk(x) # [batch, tokens, dim*3 ] # 把qkv拆分成q,v,k # rearrange tensor to [3, batch, tokens, dim] and cast to tuple q, k, v = tuple(rearrange(qkv, 'b t (d k) -> k b t d ', k=3)) # 生成结果的形状为: [batch, tokens, tokens] scaled_dot_prod = torch.einsum('b i d , b j d -> b i j', q, k) * self.scale_factor if mask is not None: assert mask.shape == scaled_dot_prod.shape[1:] scaled_dot_prod = scaled_dot_prod.masked_fill(mask, -np.inf) attention = torch.softmax(scaled_dot_prod, dim=-1) #返回查询Q对各关键字的权重(即attention)与V相乘的结果 return torch.einsum('b i j , b j d -> b i d', attention, v) |
4、测试
|
1 2 3 4 5 |
#输入dim=3 attention=SelfAttentionAISummer(3) #假设输入x为1x4x4矩阵(共4个token) x = torch.rand(1,4,4) attention(x) |
运行结果
tensor([[[-0.3127, 0.4551, -0.0695],
[-0.3176, 0.4594, -0.0715],
[-0.3133, 0.4551, -0.0703],
[-0.3116, 0.4531, -0.0702]]], grad_fn=)
einops的使用可参考官网:
https://github.com/arogozhnikov/einops