第2章 TensorFlow张量及其计算
2015年11月,Google首次宣布开源TensorFlow,经过多次迭代,2017年2月,Google发布了更加稳定并且性能更加强劲的TensorFlow 1.0。2019年10月,Google正式发布了TensorFlow 2.0, 在1.0的基础上,2.0版本的TensorFlow有以下的增强。
1)对开发者更加友好,默认为即时执行模式(Eager mode,或称为动态图模式),TensorFlow代码现在可以像正常的Python代码一样运行,这大大提高了人们的开发效率。
2)在需要提高性能的地方可利用@tf.function切换成Autograph模式。
3)Keras已经成为TensorFlow 2.0版本的官方高级API,并推荐使用tf.keras。
4)清理了大量的API,以简化和统一TensorFlow API。
5)改进tf.data功能,基于tf.data API,可使用简单的代码来构建复杂的输入。
6)提供了更加强大的跨平台能力, 通过TensorFlow Lite,我们可以在Andiord,iOS以及各种嵌入式系统里面部署和运行模型。通过TensorFlow.js,我们可以将模型部署在JavaScript环境里面。本章将从以下几个方面介绍TensorFlow基础内容。
♦ 简单说明TensorFlow 2+的安装;
♦ 层次架构;
♦ 张量与变量;
♦ 动态计算图;
♦ 自动图;
♦ 自动微分;
♦ 损失函数、优化器等;
♦ 通过实例把这些内容贯穿起来。
2.1 安装配置
TensorFlow支持多种环境,如Linux、Windows、Mac等,本章主要介绍基于Linux系统的TensorFlow安装。TensorFlow的安装又分为CPU版和GPU版。CPU版相对简单一些,无须安装显卡驱动CUDA和基于CUDA的加速库cuDNN等;GPU版的安装步骤更多一些,需要安装CUDA、cuDNN等。不过,无论选择哪种安装版本,我们推荐使用Anaconda作为Python环境,因为这样可以避免大量的兼容性和依赖性问题,而且使用其中的conda进行后续更新维护也非常方便。接下来我将简单介绍如何安装TensorFow,更详细的安装内容请参考附录A。
2.1.1 安装Anaconda
Anaconda内置了数百个Python经常使用的库。其包含的科学包有:conda、NumPy、Scipy、Pandas、IPython Notebook等,还包括机器学习或数据挖掘的库,如Scikit-learn。Anaconda是目前最好的Python安装环境,它不但便于安装,也便于后续版本升级维护。因此,本书推荐安装Anaconda。
Anaconda有Windows、Linux、MacOS等版本,这里我们以Windows环境为例,包括以下TensorFlow也是基于Windows。基于Linux的安装请参考附A。
1.下载安装包
打开Anaconda的官网(https://www.anaconda.com/products/individual),可看到如图2-1 所示的界面。
图2-1 Aanaconda下载界面
选择Python 3.8,64-Bit Graphical Installer 大小为477 MB。下载后可得类似如下文件:
Anaconda3-2021.05-Windows-x86_64.exe
2.安装
点击文件Anaconda3-2021.05-Windows-x86_64.exe即可,安装基本按默认或推荐选项即可,最后为提示是否“Add Anaconda to my PATH environment variable”,勾选,系统自动把Anaconda的安装目录写入PATH环境变量中。至此,安装结束。
3.验证
打开“Anaconda prompt”输入conda list,安装成功后可以看到已安装的库。
2.1.2 安装TensorFlow CPU版
在Windows安装TensorFlow CPU版比较简单,可以用conda或pip进行安装。
1. 使用conda安装
使用conda安装将自动安装TensorFlow依赖的模块,但因conda能安装的最新版本与TensorFlow最新版本有点滞后,如果要安装最新版本,可使用pip安装。
打开Anaconda prompt界面,先用search命令,查看用conda能安装的版本:
图2-2展示了运行结果的最后几行。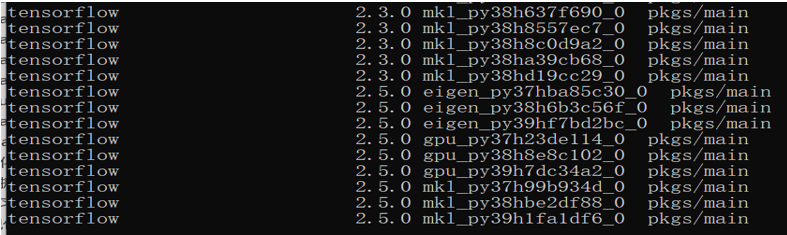
图2-2 查看conda能安装的TensorFlow(CPU版本)各版本
使用conda安装,选择版本号和安装源。如安装2.5.0 版本,使用豆瓣源。
|
|
conda install tensorflow =2.5 -i https://pypi.douban.com/simple |
然后启动Jupyter Notebook 服务,验证安装是否成功。在Jupyter Notebook中输入以下代码,如果没有报错信息,且显示已安装TensorFlow的版本为2.5.0,说明安装成功。
|
|
import tensorflow as tf print(tf.__version__) |
2.1.3 安装TensorFlow GPU版
安装TensorFlow GPU版的步骤相对多一些,这里采用一种比较简洁的方法。目前TensorFlow对CUDA的支持比较好,所以在安装GPU版之前,首先需要安装一块或多块GPU显卡。本节以NVIDIA显卡为例,当然也可以使用其他显卡。
接下来我们需要安装:
• 显卡驱动
• CUDA
• cuDNN
其中CUDA(Compute Unified Device Architecture)是英伟达公司推出的一种基于新的并行编程模型和指令集架构的通用计算架构,它能利用英伟达GPU的并行计算引擎,比CPU更高效地解决许多复杂计算任务。NVIDIA cuDNN是用于深度神经网络的GPU加速库,它强调性能、易用性和低内存开销。NVIDIA cuDNN可以集成到更高级别的机器学习架构中,其插入式设计可以让开发人员专注于设计和实现神经网络模型,而不是调整性能,也可以在GPU上实现高性能并行计算。目前大部分深度学习架构使用cuDNN来驱动GPU计算。
这里假设Windows上的显卡及驱动已安装好,如果你还没有安装显卡及驱动,可参考附录A了解安装方法。
1.查看显卡信息
如果安装好GPU显卡及驱动,在Anaconda prompt端输入nvidia-smi命令可看到如2-3所示的GPU信息。
图2-3 显示GPU及驱动的相关信息
2.安装CUDA和cuDNN
1)进入NVIDIA官网(https://developer.nvidia.com/cuda-toolkit-archive)下载对应版本的CUDA并安装。
2)进入NVIDIA官网下载对应版本的cuDNN并解压缩。解压后的文件如图2-4所示。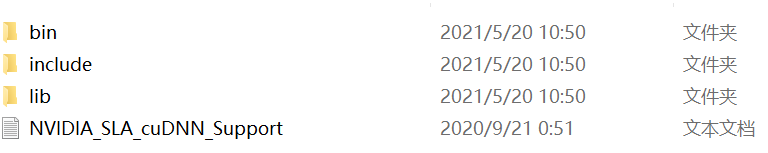
图2-4 下载cuDNN并解压
3.将文件复制到对应目录
将cuDNN中的bin、include和lib文件拷贝到CUDA的安装对应目录,如:C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.1 。
4. 验证
在命令行输入:
如果能看到如下类似信息,说明安装成功!
nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2020 NVIDIA Corporation
Built on Tue_Sep_15_19:12:04_Pacific_Daylight_Time_2020
Cuda compilation tools, release 11.1, V11.1.74
Build cuda_11.1.relgpu_drvr455TC455_06.29069683_0
5.安装tensorflow-gpu
直接使用国内的源进行安装,这样下载速度比较快。
|
|
pip install tensorflow-gpu==2.5 -i https://pypi.douban.com/simple |
安装验证:
|
|
import tensorflow as tf print(tf.__version__) print(tf.config.list_physical_devices('GPU')) |
运行结果如下:
2.5
[PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')]
如果出现类似信息,说明TensorFlow-GPU安装成功!
2.2 层次架构
TensorFlow 2.0从低到高可以分成如下6个层次架构,如图2-5所示。
图2-5 TensorFlow 2.0的层次架构图
• 最底层为硬件层,TensorFlow支持CPU、GPU或TPU。
• 第2层为网络通信层,TensorFlow支持包括gRPC、RDMA(Remote Direct Memroy Access)、GDR(GPU Dirrect)和MPI4种通信协议。
• 第3层为C++实现的内核,如实现矩阵运算、卷积运算等,内核可以跨平台分布运行。
• 第4层为Python实现的各种操作符,TensorFlow提供了封装C++内核的低级API,主要包括各种张量操作算子、计算图、自动微分等,其中大部分继承自基类tf.Module,具体包括tf.Variable,tf.constant,tf.function, tf.GradientTape,tf.nn.softmax等。
• 第5层为Python实现的模型组件,TensorFlow对低级API进行了函数封装,主要包括各种模型层,损失函数,优化器,数据管道,特征列等。如tf.keras.layers,tf.keras.losses,tf.keras.metrics,tf.keras.optimizers,tf.data.DataSet等。
• 第6层为Python实现的各种模型,一般为TensorFlow按照面向对象方式封装的高级API,主要为tf.keras.models提供的模型的类接口。
接下来就各层的主要内容进行说明。
2.3 张量
张量(Tensor)是具有统一类型(通常是整型或者浮点类型)的多维数组,它和NumPy里面的ndarray非常相似。TensorFlow的张量(tf.Tensor)的基本属性与ndarray类似,具有数据类型和形状维度等,同时TensorFlow提供了丰富的操作库(tf.add,tf.matmul,tf.linalg.inv等),它们使用和生成tf.Tensor。 tf.Tensor与NumPy还可以互相转换。除这些相似点之外,tf.Tensor与NumPy也有很多不同之处,最大的不同就是NumPy只能在CPU上计算,没有实现GPU加速计算,而tf.Tensor不但可以在CPU上计算,也可以在GPU加速计算。接下来,我们就张量的基本属性、基本操作进行简单说明,同时总结了tf.Tensor与NumPy的异同点。
2.3.1 张量的基本属性
张量有几个重要的属性。
• 形状(shape):张量的每个维度的长度,与NumPy数组的shape一样。
• 维度/轴(axis):可以理解为数组的维度,例如,二维数组或者三维数组等。
• 秩(rank): 张量的维度数量,可用ndim查看。
• 大小(size): 张量的总的项数,也就是所有元素的数量,与NumPy数组的size一样。
• 数据类型(dtype): 张量元素的数据类型,如果在创建张量时不指定,TensorFlow会自动选择合适的数据类型。
接下来通过一些实例进行说明。用tf.constant生成各种维度的张量:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import tensorflow as tf import numpy as np # 这个张量没有轴(不是数组),被称作0秩张量,也被称为标量 rank_0_tensor = tf.constant(5) print(rank_0_tensor) # tf.Tensor(5, shape=(), dtype=int32) # 这个张量有一个轴,被称作1秩张量,也被称为向量。 rank_1_tensor = tf.constant([5, 4 ,3, 2, 1]) print(rank_1_tensor) # tf.Tensor([5 4 3 2 1], shape=(5,), dtype=int32) # 这个张量有两个轴,被称作2秩张量,也被称为矩阵。 rank_2_tensor = tf.constant([[5, 4 ,3, 2, 1], [1, 2, 3, 4, 5]]) print(rank_2_tensor) # tf.Tensor([[5 4 3 2 1] [1 2 3 4 5]], shape=(2, 5), dtype=int32) |
我们看一个4维的张量及相关属性。
|
|
rank_4_tensor = tf.zeros([3, 2, 4, 5]) |
这是一个秩为4,形状为(3,2,4,5)的张量,各轴的大小与张量形状之间的对应关系,可参考图2-6。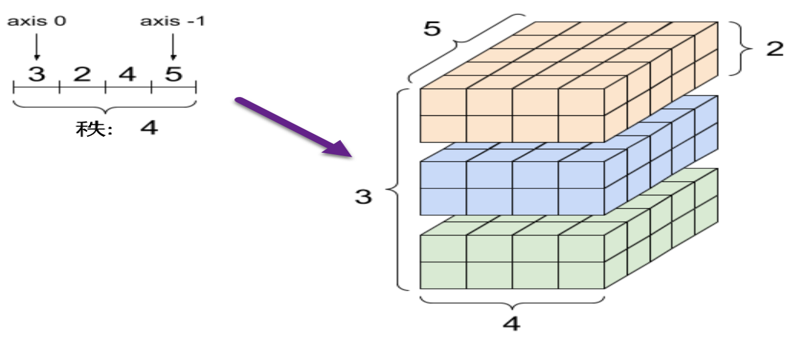
图2-6 张量各轴大小与张量形状之间对应关系
轴一般按照从全局到局部的顺序进行排序:首先是批次轴,随后是空间维度,最后是每个位置的特征。这样,在内存中,特征向量就会位于连续的区域。
2.3.2 张量切片
张量切片与NumPy切片一样,也是基于索引。切片或者索引是Python语言中针对字符串、元祖或者列表进行读写的魔法方法,在第1章介绍NumPy的时候也提到过,针对NumPy数组,我们也可以进行索引或者切片操作。同样的,我们也可以对TensorFlow里面的张量进行索引或者切片操作,并且遵循Python语言或者说NumPy数组的索引规则。
• 索引从下标0开始。
• 负索引按照倒叙进行索引,比如 -1表示倒数第一个元素。
• 切片的规则是start:stop:step。
• 通过制定多个索引,可以对多维度张量进行索引或者切片。
示例如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
# 生成一维张量 tf_tensor = tf.constant([1,2,3,4,5,6,7,8,9,10]) #对1秩张量进行索引和切片 # 取张量的第二个元素 print(tf_tensor[1].numpy()) # 2 # 取张量中的第二个元素以及之后的元素,输出结果为一个数组 print(tf_tensor[1:].numpy()) # [ 2 3 4 5 6 7 8 9 10] # 取张量中的第二个元素以及之后的元素,并且没两个元素取一个,输出结果为一个数组 print(tf_tensor[1::2].numpy()) # [ 2 4 6 8 10] #生成二维张量 tf_tensor = tf.constant([[1,2,3,4,5],[6,7,8,9,10]]) # 对2秩张量进行索引和切片 # 取张量的第二行 print(tf_tensor[1].numpy()) # [ 6 7 8 9 10] # 取张量的第二行 print(tf_tensor[1,:].numpy()) # [ 6 7 8 9 10] # 去第二行的元素,注意,这里不改变张量的维度 print(tf_tensor[1:,1:].numpy()) # [[ 7 8 9 10]] |
2.3.3 操作形状
与NumPy中的reshape、transpose函数一样,TensorFlow也提供reshape、transpose函数帮助我们操作张量形状。
通过重构可以改变张量的形状。重构的速度很快,资源消耗很低,因为不需要复制底层数据,只是形成一个新的视图,原张量并没有改变。
|
|
#生成一个3维张量 rank_3_tensor = tf.constant([[[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]], [[10, 11, 12, 13, 14],[15, 16, 17, 18, 19]], [[20, 21, 22, 23, 24],[25, 26, 27, 28, 29]]]) |
数据在内存中的布局保持不变,同时使用请求的形状创建一个指向同一数据的新张量。TensorFlow 采用 C 样式的“行优先”内存访问顺序,即最右侧的索引值递增对应于内存中的单步位移。
|
|
#把3维张量平铺为向量 print(tf.reshape(rank_3_tensor, -1)) |
运行结果如下:
tf.Tensor(
[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29], shape=(30,), dtype=int32)
一般来说,tf.reshape 唯一合理的用途是用于合并或拆分相邻轴(或添加/移除 1维)。 对于3x2x5 张量,重构为(3x2)x5或者3x(2x5) 都是合理的,因为切片不会混淆。
|
|
print(tf.reshape(rank_3_tensor, [3*2, 5]), "\n") print(tf.reshape(rank_3_tensor, [3, -1])) |
运行结果如下:
tf.Tensor(
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]
[20 21 22 23 24]
[25 26 27 28 29]], shape=(6, 5), dtype=int32)
tf.Tensor(
[[ 0 1 2 3 4 5 6 7 8 9]
[10 11 12 13 14 15 16 17 18 19]
[20 21 22 23 24 25 26 27 28 29]], shape=(3, 10), dtype=int32)
重构可以处理总元素个数相同的任何新形状,但是如果不遵从轴的顺序,则不会发挥任何作用。利用 tf.reshape 无法实现轴的交换,所以要交换轴,需要使用 tf.transpose。
2.4 变量
深度学习在训练模型时,用变量来存储和更新参数。建模时它们需要被明确地初始化,模型训练后它们必须被存储到磁盘。这些变量的值可在之后模型训练和分析时被加载。变量通过tf.Variable类进行创建和跟踪,对变量执行运算可以改变其值。可以利用特定运算读取和修改变量的值,也可以通过使用张量或者数组的形式创建新的变量:
|
|
import tensorflow as tf #用tf.Variable生成变量 var = tf.Variable([[1, 2, 3],[4, 5, 6]]) print(var,'\n') tensor = tf.constant([[1, 2, 3],[4, 5, 6]]) var=tf.Variable(tensor) print(var) |
运行结果如下:
<tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[1, 2, 3], [4, 5, 6]])>
<tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[1, 2, 3], [4, 5, 6]])>
变量与常量的定义方式以及操作行为都十分相似,实际上,它们都是tf.Tensor支持的一种数据结构。与常量类似,变量也有数据类型 dtype 和形状 shape,也可以与NumPy数组相互交换,并且大部分能够作用于常量的运算操作都可以应用于变量,除了进行形状变形(变量的reshape方法会生成一个新的常量)。示例如下:
|
|
import tensorflow as tf var = tf.Variable([[1, 2, 3],[4, 5, 6]]) # 变量类型 print(type(var),"\n") # 变量可以转换成NumPy数组 print(var.numpy(),"\n") # 对变量执行reshape操作不会改变变量,而是生成一个新的常量 print(type(tf.reshape(var, [3,2])),"\n") #原变量属性不变 print(var) |
运行结果如下:
<class 'tensorflow.python.ops.resource_variable_ops.ResourceVariable'>
[[1 2 3]
[4 5 6]]
<class 'tensorflow.python.framework.ops.EagerTensor'>
<tf.Variable 'Variable:0' shape=(2, 3) dtype=int32, numpy= array([[1, 2, 3], [4, 5, 6]])>
2.5 NumPy与tf.tensor比较
前文提到, NumPy数组与TenosrFlow中的张量(即tf.tensor)有很多相似地方,而且可以互相转换。表2-1总结了NumPy与tf.tensor的异同点。
表2-1 NumPy与tf.tensor的异同点
| 操作类别 |
NumPy |
TensorFlow 2+ |
| 数据类型 |
np.ndarray |
tf.Tensor |
| np.float32 |
tf.float32 |
| np.float64 |
tf.double |
| np.int64 |
tf.int64 |
| 从已有数据构建 |
np.array([3.2, 4.3], dtype=np.float16) |
a=tf.constant([3.2, 4.3], dtype=tf.float16)#常量
v=tf.Variable([3.2, 4.3], dtype=tf.float16)#变量 |
| x.copy() |
tf.identity(x);
tf.tile(a,(n,m))# 元组里的每个数值对应该轴复制次数 |
| np.concatenate |
tf.concat((a,b),axis)# 待拼接的轴对应的维度数值可以不等,但其他维度形状需一致
tf.stack((a,b),axis)# 带堆叠张量的所有维度数值必须相等 |
| 线性代数 |
np.dot #内积
np.multiply(*)#逐元素相乘或哈达玛积 |
tf.matmul(x, y, name=None) 或(@)#内积
tf.multiply(x, y, name=None),或(*)#逐元素相乘或哈达玛积 |
| 属性 |
x.ndim |
x.ndim #查看rank |
| x.shape |
x.shape |
| x.size |
tf.size(x) |
| 改变形状 |
x.reshape |
tf.reshape(x,(n,(-1)))#-1表示自动计算其他维度 |
| np.transpose(x, [新的轴顺序] ) |
tf.transpose(x, [新的轴顺序] ) |
| x.flatten() |
tf.reshape(x,[-1]);
tf.keras.layers.Flatten() |
| 维度增减 |
np.expand_dims(arr, axis) |
tf.expend_dims(a,axis) |
| np.squeeze(arr, axis) |
tf.squeeze(a,axis),#如果不声明axis,那么将压缩所有数值为1的维度。 |
| 类型转换 |
np.floor(x) |
x=tf.cast(x,dtype=XX)
x=x.numpy()=>np.array |
| 比较 |
np.less |
tf.less(x,threshold) |
| np.less_equal |
tf.less_equal(x, threshold) |
| np.greater_equal |
tf.greater_equal(x, threshold) |
| 随机种子 |
np.random.seed |
tf.random.set_seed(n) |
它们可以互相转换,具体分析如下:
• 通过使用 np.array 或 tensor.numpy 方法,可以将TensorFlow张量转换为 NumPy 数组;
• tf.convert_to_tensor把Python对象(NumPy,list、tuple等),或使用tf.constant、tf.Variable把Python对象转换为TensorFlow张量。
2.6 动态计算图
TensorFlow有3种计算图:TensorFlow1.0时代的静态计算图,TensorFlow 2.0时代的动态计算图和Autograph。静态计算图,需要先使用TensorFlow的各种算子创建计算图,再开启一个会话(Session)执行计算图。 而在TensorFlow 2.0时代,默认采用的是动态计算图,即每使用一个算子后,该算子会被动态加入隐含的默认计算图中立即执行并获取返回结果,而无须执行Session。
使用动态计算图(即Eager Excution立即执行)的好处是方便调试程序,执行TensorFlow代码犹如执行Python代码一样,而且可以使用Python,非常便捷。不过使用动态计算图的坏处是运行效率相对会低一些,因为在执行动态图期间会有许多次Python进程和TensorFlow的C++进程之间的通信。而静态计算图不通过Python这个中间环节,基本在TensorFlow内核上使用C++代码执行,效率更高。
为了兼顾速度与性能,在TensorFlow 2.0中可以使用@tf.function装饰器将普通Python函数转换成对应的TensorFlow计算图构建代码。与执行静态图方式类似,使用@tf.function构建静态图的方式叫作Autograph(自动图),更多详细内容将在2.7节介绍。
2.6.1 静态计算图
在TensorFlow 1.0中,静态计算图的使用过程一般分两步:第1步是定义计算图,第2步是在会话中执行计算图。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import tensorflow as tf #定义计算图 grap = tf.Graph() with grap.as_default(): #placeholder为占位符,执行会话时候指定填充对象 x = tf.placeholder(tf.float32,shape=[],name='x') y = tf.placeholder(tf.float32,shape=[],name='y') b= tf.Variable(15.0,dtype=tf.float32) z=tf.multiply(x,y,name='c')+b #初始化参数 init_op = tf.global_variables_initializer() #执行计算图 with tf.Session(graph = grap) as sess: sess.run(init_op) print(sess.run(fetches = z,feed_dict = {x:20,y:36,b:2})) |
以上代码在TensorFlow 2.0环境中将报错,因为该环境中已取消了占位符(placeholder)及会话(Session)等内容,不过为考虑对老版本Tensorflow 1.0的兼容性,在tf.compat.v1子模块中保留了对TensorFlow 1.0那种静态计算图构建风格的支持,但是加上tf.compat.v1来对老版本提供支持的这种方式并不是官方推荐使用的方式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import tensorflow as tf #定义计算图 grap = tf.compat.v1.Graph() with grap.as_default(): #placeholder为占位符,执行会话时候指定填充对象 x = tf.compat.v1.placeholder(tf.float32,shape=[],name='x') y = tf.compat.v1.placeholder(tf.float32,shape=[],name='y') b = tf.compat.v1.Variable(15.0,dtype=tf.float32) z=tf.multiply(x,y,name='c')+b #初始化参数 init_op = tf.compat.v1.global_variables_initializer() #执行计算图 with tf.compat.v1.Session(graph = grap) as sess: sess.run(init_op) print(sess.run(fetches = z,feed_dict = {x:20,y:36})) |
运行结果如下:
735.0
2.6.2 动态计算图
以上代码如果采用动态计算图的方式实现,需要做如下处理。
1)把占位符改为其他张量,如tf.constant或tf.Variable。
2)无须显式创建计算图。
3)无须变量的初始化。
4)无须执行Session,把sess.run中的feed_dict改为传入函数的参数,fetches改为执行函数即可。
采用TensorFlow 2.0动态图执行的方式,代码如下:
|
|
import tensorflow as tf #定义常量或变量 x=tf.constant(20,dtype=tf.float32) y=tf.constant(36,dtype=tf.float32) #定义函数 def mul(x,y): #定义常量或变量 b=tf.Variable(15 ,dtype=tf.float32) z=tf.multiply(x,y,name='c')+b return z #执行函数 print(mul(x,y).numpy()) |
运行结果如下:
735.0
2.7 自动图
与静态计算图相比,动态计算图虽然调试编码效率高但是执行效率偏低,TensorFlow 2.0 之后的自动图(AutoGraph)可以将动态计算图转换成静态计算图,兼顾开发效率和执行效率。通过给函数添加@tf.function装饰器就可以实现AutoGraph功能,但是在编写函数时需要遵循一定的编码规范,否则可能达不到预期的效果,这些编码规范主要包括如下几点。
• 避免在函数内部定义变量(tf.Variable)。
• 函数体内应尽可能使用TensorFlow中的函数而不是Python语言自有函数。比如使用tf.print而不是print,使用tf.range而不是range,使用tf.constant(True)而不是True。
• 函数体内不可修改该函数外部的Python列表或字典等数据结构变量。
用@tf.fuction装饰2.6.2节的函数,把动态计算图转换为自动图。
|
|
import tensorflow as tf #定义常量或变量 x=tf.constant(20,dtype=tf.float32) y=tf.constant(36,dtype=tf.float32) #定义函数 @tf.function def mul(x,y): #定义常量或变量 b=tf.Variable(15 ,dtype=tf.float32) z=tf.multiply(x,y,name='c')+b return z #执行函数 print(mul(x,y).numpy()) |
运行代码,出现如下错误信息:
ValueError: tf.function-decorated function tried to create variables on non-first call
这是为什么呢?
报错是因为函数定义中定义了一个tf.Variable变量。实际上,在动态模式中,这个对象就是一个普通的Python对象,在定义范围之外会被自动回收,然后在下次运行时被重新定义,因此不会有错误。但是现在tf.Variable定义了一个持久的对象,如果函数被@tf.function修饰,动态模型被禁止,tf.Variable定义的实际上是图中的一个节点,而这个节点不会被自动回收,且图一旦编译成功,不能再创建变量。故执行函数时会报这个错误。
那么,如何避免这样的错误呢?方法有多种,列举如下。
1)把tf.Variable变量移到被@tf.function装饰的函数外面。
|
|
import tensorflow as tf #定义常量或变量 x=tf.constant(20,dtype=tf.float32) y=tf.constant(36,dtype=tf.float32) #定义常量或变量 b=tf.Variable(15 ,dtype=tf.float32) #定义函数 @tf.function def mul(x,y): z=tf.multiply(x,y,name='c')+b return z #执行函数 print(mul(x,y).numpy()) |
运行结果如下:
735.0
在函数外部定义tf.Variable变量,你可能会感觉这个函数有外部变量依赖,封装不够完美。那么,是否有两全其美的方法呢?利用类的封装性就可以完美解决这个问题,即创建一个包含该函数的类,并将相关的tf.Variable创建放在类的初始化方法中。
2)通过封装成类方法来解决这个问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import tensorflow as tf #定义一个类 class Test_Mul: def __init__(self): super(Test_Mul, self).__init__() self.b=tf.Variable(15 ,dtype=tf.float32) @tf.function def mul(self,x,y): z=tf.multiply(x,y,name='c')+self.b return z #执行函数 x=tf.constant(20,dtype=tf.float32) y=tf.constant(36,dtype=tf.float32) Test=Test_Mul() print(Test.mul(x,y).numpy()) |
运行结果如下:
735.0
其他两个规范比较好理解,后面章节将详细说明。
2.8 自动微分
机器学习,尤其是其中的深度学习,通常依赖反向传播求梯度来更新网络参数,求梯度通常非常复杂且容易出错。 可喜的是TensorFlow深度学习架构帮助我们自动地完成了求梯度运算。 Tensorflow一般使用梯度磁带tf.GradientTape来记录正向运算过程,然后使用反播磁带自动得到梯度值。 这种利用tf.GradientTape求微分的方法叫作Tensorflow的自动微分机制,其基本流程如图2-7所示。
图2-7 TensorFlow自动微分的流程图
以下通过一些示例进行说明:
|
|
import tensorflow as tf import numpy as np # f(x) = a*x**2 + b*x + c的导数 #默认情况,张量tf.constant为常量,只有变量tf.Variable作为参数更新 x = tf.Variable(0.0,name = "x",dtype = tf.float32) a = tf.constant(1.0) b = tf.constant(5.0) c = tf.constant(2.0) #对函数y实现自动求导 with tf.GradientTape() as tape: y = a*tf.pow(x,2) + b*x + c dy_dx = tape.gradient(y,x) print(dy_dx) |
对常量张量也可以求导,需要增加watch。例如:
|
|
with tf.GradientTape() as tape: tape.watch([a,b,c]) y = a*tf.pow(x,2) + b*x + c dy_dx,dy_da,_,dy_dc = tape.gradient(y,[x,a,b,c]) print(dy_da) print(dy_dc) |
利用tape嵌套方法,可以求二阶导数。
|
|
with tf.GradientTape() as tape2: with tf.GradientTape() as tape1: y = a*tf.pow(x,2) + b*x + c dy_dx = tape1.gradient(y,x) dy2_dx2 = tape2.gradient(dy_dx,x) print(dy2_dx2) |
默认情况下,只要调用GradientTape.gradient方法,系统将自动释放 GradientTape保存的资源。要在同一计算图中计算多个梯度,可创建一个 persistent=True 的梯度磁带,这样便可以对 gradient 方法进行多次调用。最后用del显式方式删除梯度磁带,例如:
|
|
x = tf.constant([1, 2.0]) with tf.GradientTape(persistent=True) as tape: tape.watch(x) y = x * x z = y * y print(tape.gradient(y, x).numpy()) print(tape.gradient(z, x).numpy()) del tape #释放内存 |
梯度磁带会自动监视 tf.Variable,但不会监视 tf.Tensor。如果无意中将变量(tf.Variable)变为常量(tf.Tensor)(如tf.Variable 与一个tf.Tensor相加,其和就变成常量了),梯度磁带将不再监控tf.Tensor。 为避免这种情况,可使用 Variable.assign 给tf.Variable赋值,示例如下:
|
|
x = tf.Variable(2.0) for epoch in range(2): with tf.GradientTape() as tape: y = x+1 dy_x=tape.gradient(y, x) #print(type(x).__name__, ":", tape.gradient(y, x)) print(dy_x) #变量变为常量tf.Tensor x = x + 1 # This should be `x.assign_add(1)` |
运行结果如下:
tf.Tensor(1.0, shape=(), dtype=float32)
None
如果在函数的计算中有TensorFlow 之外的计算(如使用NumPy算法),则梯度带将无法记录梯度路径;同时,如果变量的值为整数,则无法求导。例如:
|
|
x = tf.Variable([[1.0, 2.0], [3.0, 4.0]], dtype=tf.float32) with tf.GradientTape() as tape: x2 = x**2 # 使用TensorFlow之外的算子np.mean,它将把结果变为常量,梯度带将无法记录梯度路径 y = np.mean(x2, axis=0) y1 = tf.reduce_mean(y, axis=0) print(tape.gradient(y1, x)) #None |
2.9 损失函数
TensorFlow内置很多损失函数(又称为目标函数),在tf.keras模块中有很多,这里仅列出一些常用的模块及功能说明,且有些还容易搞混,所以这里就此做进一步说明。
用于分类的损失函数如下所示。
• binary_crossentropy(二元交叉熵):用于二分类,参数from_logits说明预测值是否是logits(logits没有使用sigmoid激活函数全连接的输出),类实现形式为 BinaryCrossentropy
• categorical_crossentropy(类别交叉熵):用于多分类,要求标签(label)为独热(One-Hot)编码(如:[0,1,0]),类实现形式为CategoricalCrossentropy
• sparse_categorical_crossentropy(稀疏类别交叉熵):用于多分类,要求label为序号编码形式(一般取整数),类实现形式为 SparseCategoricalCrossentropy
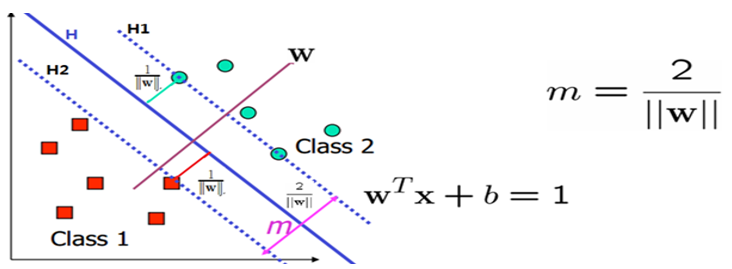
• hinge(合页损失函数): 用于二分类,最著名的应用是作为支持向量机SVM的损失函数,类实现形式为 Hinge。
用于回归的损失函数如下所示。
• mean_squared_error(平方差误差损失):用于回归,简写为 mse, 类实现形式为 MeanSquaredError 和 MSE。
• mean_absolute_error (绝对值误差损失):用于回归,简写为 mae, 类实现形式为 MeanAbsoluteError 和 MAE。
• mean_absolute_percentage_error (平均百分比误差损失):用于回归,简写为 mape, 类实现形式为 MeanAbsolutePercentageError 和 MAPE。
• Huber(Huber损失):只有类实现形式,用于回归,介于mse和mae之间,对异常值进行比较。鲁棒,相对mse有一定的优势。
2.10优化器
优化器(optimizer)在机器学习中占有重要地位,它是优化目标函数的核心算法。在进行低阶编程时,我们通常使用apply_gradients方法把优化器传入变量和对应梯度,从而对给定变量进行迭代,或者直接使用minimize方法对目标函数进行迭代优化。
在实现中高级阶API编程时,我们往往会在编译时将优化器传入Keras的Model,通过调用model.fit实现对Loss的的迭代优化。优化器与tf.Variable一样,一般需要在@tf.function外创建。
tf.keras.optimizers和tf.optimizers 完全相同,tf.optimizers.SGD即tf.keras.optimizers.SGD。最常用的优化器列举如下。
1.随机梯度下降法(Stochastic Gradient Descent,SGD)
tf.keras.optimizers.SGD默认参数为纯SGD, 其语法格式为:
|
|
tf.keras.optimizers.SGD(learning_rate=0.01, momentum=0.0, nesterov=False, name='SGD', **kwargs) |
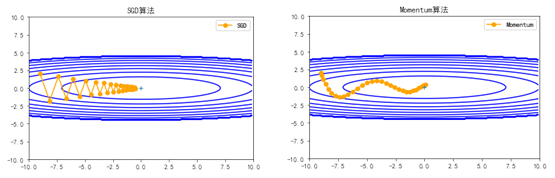
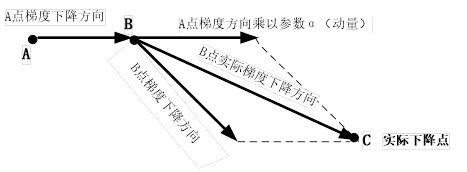
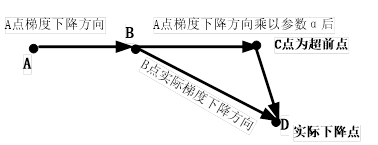
设置momentum参数不为0,SGD实际上变成SGDM, 如果仅考虑一阶动量, 设置 nesterov为True后SGDM变成NAG,即 Nesterov Accelerated Gradient,在计算梯度时计算的是向前走一步所在位置的梯度。
2.自适应矩估计 (Adaptive Moment Estimation,Adam)
tf.keras.optimizers.Adam, 其语法格式为:
|
|
tf.keras.optimizers.Adam( learning_rate=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-07, amsgrad=False,name='Adam', **kwargs) |
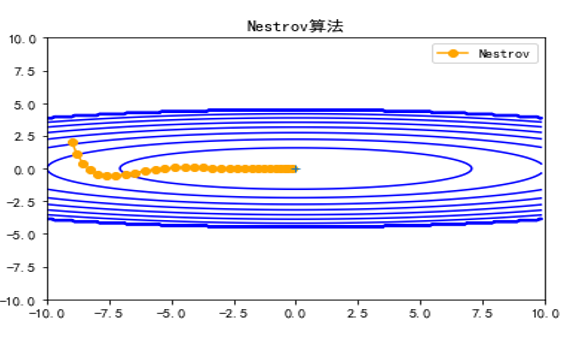
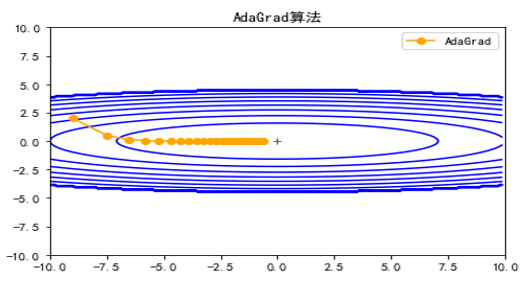
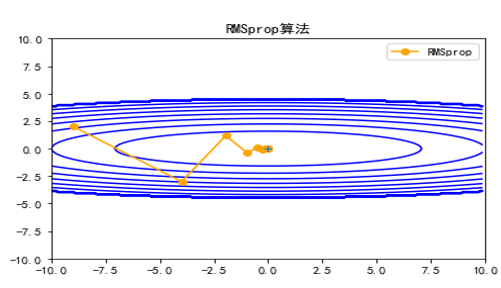
它是自适应(所谓自适应主要是自适应学习率)优化器的典型代表,同时考虑了一阶动量和二阶动量,可以看成是在RMSprop的基础上进一步考虑了一阶动量。自适应类的优化器还有Adagrad、RMSprop、Adadelta等。
2.11 TensorFlow 2.0实现回归实例
在1.7节,我们用纯NumPy实现一个回归实例,这里我们使用TensorFlow 2.0中的自动微分来实现。数据一样,目标一样,但实现方法不一样,大家可以进行比较。
1. 生成数据
这些内容与1.7节的内容一样,只是需要把NumPy数据转换TensorFlow格式的张量或变量。
|
|
import tensorflow as tf import numpy as np from matplotlib import pyplot as plt np.random.seed(100) x0 = np.linspace(-1, 1, 100).reshape(100,1) y0 = 3*np.power(x0, 2) +2+ 0.2*np.random.rand(x0.size).reshape(100,1) # 画图 plt.scatter(x, y) plt.show() |
运行结果如图2-8所示。
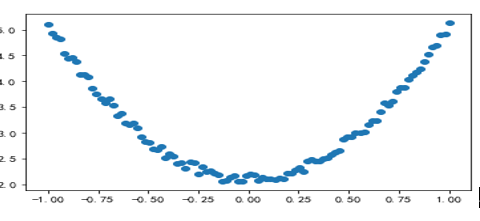
图2-8 回归使用的数据图形
2. 把numpy转换为TensorFlow 2.0格式的张量或变量
|
|
x=tf.constant(x0) y=tf.constant(y0) # 随机初始化参数 w0= np.random.rand(1,1) b0 = np.random.rand(1,1) |
3.定义回归模型
|
|
class LinearRegression: #定义构建函数,初始化权重参数 def __init__(self,**args): super().__init__(*args) self.w=tf.Variable(w0) self.b=tf.Variable(b0) #定义__call__函数,该模型为单层神经网络,其正向传播操作 def __call__(self,x): y1= tf.square(x)*self.w + self.b return y1 mymodel=LinearRegression() |
4.自定义损失函数
|
|
#自定义损失函数 def myloss(x,y): mse=tf.reduce_mean(tf.square(y - mymodel(x))) return mse |
5.使用自动微分及自定义梯度更新方法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
lr=0.001 @tf.function def train_step(x,y,model,epoch): for i in range(epoch): with tf.GradientTape() as tape: loss=myloss(x,y) # 反向传播求梯度 w=model.w b=model.b dw,db=tape.gradient(loss,[w,b]) # 梯度下降法更新参数 w.assign(w - lr*dw) b.assign(b - lr*db) if i%50==0: tf.print(w) tf.print(loss) tf.print() return w,b |
对模型进行训练。
|
|
train_step(x,y,mymodel,1000) |
比较拟合程度。
|
|
plt.scatter(x, y, c="b") plt.scatter(x, mymodel(x), c="r") plt.show() |
使用TensorFlow实现回归问题的拟合结果如图2-9所示。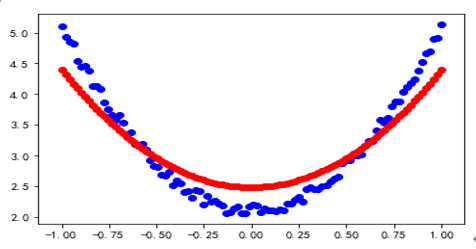
图2-9 使用TensorFlow实现回归问题的拟合结果
6.使用自动微分及优化器
虽然上述梯度计算采用自动微分的方法,但梯度更新采用自定义方式,如果损失函数比较复杂,自定义梯度难度会徒增,是否有更好的方法呢?使用优化器可以轻松实现自动微分、自动梯度更新,而这正是方向传播的核心内容。
使用优化器(optimizer)的常见方法有3种,介绍如下。
1)使用apply_gradients方法:先计算损失函数关于模型变量的导数,然后将求出的导数值传入优化器,使用优化器的 apply_gradients 方法迭代更新模型参数以最小化损失函数。
2)用minimize方法:minimize(loss, var_list) 计算loss所涉及的变量(tf.Varialble)组成的列表或者元组,即tf.trainable_variables(),它是compute_gradients()和apply_gradients()这两个方法的简单组合。用代码可表示如下:
|
|
#计算变量列表的梯度 grads_and_vars = opt.compute_gradients(loss, ) # grads_and_vars是元组(gradient, variable).构成的列表 # 使用优化器optimizer更新梯度. opt.apply_gradients(grads_and_vars) |
3)在编译时将优化器传入Keras的Model,通过调用model.fit实现对loss的的迭代优化。具体实例可参考本书3.3节。
下面,我们先来了解如何使用优化器的apply_gradients方法。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
lr=0.001 optimizer = tf.keras.optimizers.SGD(learning_rate=0.01) @tf.function def train_step01(x,y,model,epoch): for i in range(epoch): with tf.GradientTape() as tape: loss=myloss(x,y) # 说明权重参数 w=model.w b=model.b #自动计算损失函数,并返回自变量(模型参数)的梯度 dw,db=tape.gradient(loss,[w,b]) #根据梯度自动更新参数,这就实现了梯度反向传播 optimizer.apply_gradients(grads_and_vars=zip([dw,db],[w,b])) # 以下更新梯度步骤就不需要了! #w.assign(w - lr*dw) #b.assign(b - lr*db) if i%50==0: tf.print(w) tf.print(loss) tf.print() return w,b |
训练模型。
|
|
train_step01(x,y,mymodel,1000) |
使用自动微分的拟合结果如图2-10所示。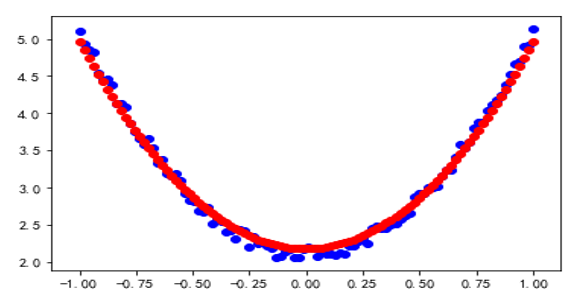
图2-10 使用自动微分的拟合结果
由此可见,使用优化器不但可以使程序更简洁,也可以使模型更高效!
接下来,我们使用优化器的minimize(loss, var_list) 方法更新参数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
lr=0.001 #自定义损失函数 w=tf.Variable(w0,name = "w") b=tf.Variable(b0,name = "b") def myloss02(): y1= tf.square(x)*w + b mse=tf.reduce_mean(tf.square(y - y1)) return mse optimizer = tf.keras.optimizers.SGD(learning_rate=0.01) @tf.function def train_step02(epoch): for i in range(epoch): optimizer.minimize(myloss02,var_list=[w,b]) if i%100==0: tf.print(w) tf.print(b) tf.print() return w,b |
训练模型。
使用优化器的拟合结果如图2-11所示。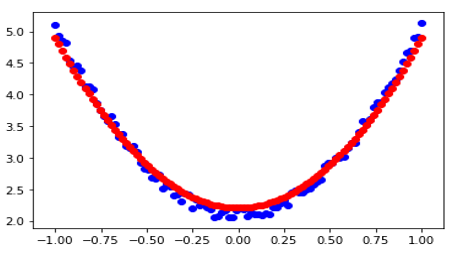
图2-11 使用优化器的拟合结果
综上,使用优化器的minimize方法更简洁。
2.12 GPU加速
深度学习的训练过程一般会非常耗时,多则通常需要几个小时或者几天来训练一个模型。如果数据量巨大、模型复杂,甚至需要几十天来训练一个模型。一般情况下,训练模型的时间主要耗费在准备数据和参数迭代上。当准备数据成为训练模型的主要瓶颈时,我们可以使用多线程来加速。当参数迭代成为训练模型的主要瓶颈时,我们可以使用系统的GPU(或TPU)资源来加速。
如果没有额外的标注,TensorFlow将自动决定是使用CPU还是GPU。 如果有必要,TensorFlow也可以在CPU和GPU内存之间复制张量。
查看系统的GPU资源以及张量的存放位置(系统内存还是GPU):
|
|
import tensorflow as tf x = tf.random.normal((5, 5)) print("设备类型: "), print(tf.config.list_physical_devices()) # 设备类型: # [PhysicalDevice(name='/physical_device:CPU:0', device_type='CPU'), PhysicalDevice(name='/physical_device:GPU:0', device_type='GPU')] print("X的存储信息: "), print(x.device) # X的存储信息: # /job:localhost/replica:0/task:0/device:GPU:0 |
在必要时,我们可以显式地指定希望的常量的存储位置以及是使用CPU还是GPU进行科学计算。如果没有显式地指定,TensorFlow将自动决定在哪个设备上执行,并且把需要的张量复制到对应的设备上。但是,在需要的时候,我们也可以用tf.device这个上下文管理器来指定设备。下面通过一个列子来说明。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import tensorflow as tf import time cpu_times = [] sizes = [1, 10, 100, 500, 1000, 2000, 3000, 4000, 5000, 8000, 10000] for size in sizes: start = time.time() with tf.device('cpu:0'): v1 = tf.Variable(tf.random.normal((size, size))) v2 = tf.Variable(tf.random.normal((size, size))) op = tf.matmul(v1, v2) cpu_times.append(time.time() - start) print('cpu 运算耗时: {0:.4f}'.format(time.time() - start)) gpu_times = [] for size in sizes: start = time.time() with tf.device('gpu:0'): v1 = tf.Variable(tf.random.normal((size, size))) v2 = tf.Variable(tf.random.normal((size, size))) op = tf.matmul(v1, v2) gpu_times.append(time.time() - start) if size % 100==0: print('gpu 运算耗时: {0:.4f}'.format(time.time() - start)) |
从上面的日志中我们可以发现,在数据量不是很大的情况下(比如矩阵大小在100100以内),使用GPU运算并没有太多的优势,这是因为前期的张量准备以及复制耗费了太多时间。但是随着数据量的逐步增加,GPU的运算速度的优势逐步体现出来,在我们的数据是一个10000 * 10000 的矩阵的时候,CPU和GPU的运算速度会有1000倍的差距。我们把数据罗列在图表上会更加直观:
|
|
import tensorflow as tf import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['font.sans-serif']=['SimHei'] plt.rcParams['axes.unicode_minus'] = False plt.title('CPU and GPU 耗时比较') plt.xlabel('矩阵大小') plt.ylabel('耗时(秒)') plt.plot(sizes,cpu_times, color=(1, 0, 0), label='CPU') plt.plot(sizes,gpu_times, color=(0, 0, 1), label='GPU') plt.legend(loc='best') plt.show() |
CPU与GPU耗时比较图如图2-12所示。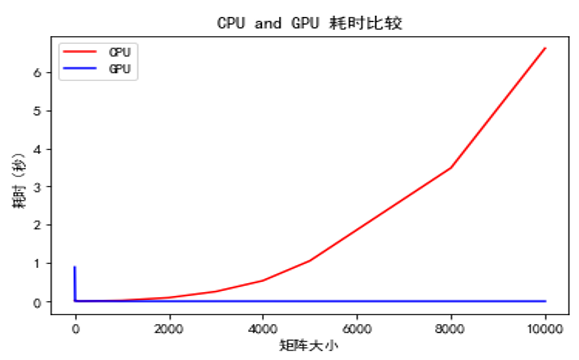
图2-12 CPU与GPU耗时比较图
2.13小结
首先简单介绍TensorFlow 2+版本的安装,然后介绍了TensorFlow的一些基本概念,如张量、变量以及计算图的几种方式等,同时与TensorFlow 1+版本的对应概念进行了比较。随后,对TensorFlow几个核心内容,如自动微分、损失函数、优化器等进行说明。为帮助大家更好地理解这些概念和方法,最后通过几个相关实例进行详细说明。








![loss(x,class)=-log(\frac {exp(x[class])}{(\sum_j exp(x[j]))})=-x[class]+log(\sum_j exp (x[j])) \tag{5.10}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b3f471c587c26fa52254b4dd62909b7b.gif)
))\tag{5.11}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_3cc131b0fe37043f12ba6216f18f5f90.gif)

















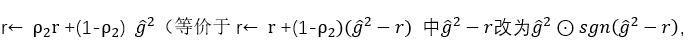








































![W=[w1,w2],X=[x1,x2] or [x,y]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b88572d7864ded7e56c46782e8dc4822.gif)