6.2奇异值分解

有关奇异值分解的几个问题
（1）可分解任何形状的矩阵？
（2）如何分解？分解步骤如何？
（3）特征值的信息量如何度量？
（4）如何利用特征值实现矩阵的近似表示？
（5）奇异值分解还存在哪些不足？如何克服这些不足？
下面就这些问题逐一进行说明

6.2.1 分解矩阵的形状

特征值分解的矩阵都是方阵，有些还需要是对称方阵。奇异值分解，没有这个限制，非方阵也可以。所以奇异值分解的应用非常广泛。

6.2.2 矩阵奇异值分解推导详细过程

根据上节特征值分解可知，对称矩阵A可以分解为：
A=Q\wedge Q^T=Q\wedge Q^{-1}\tag{6.3}
其中矩阵Q是矩阵A的正交化的特征向量，\wedge为对角矩阵，其值为A的特征值。
由式（6.3）可得：
AQ=Q\wedge\tag{6.4}
正交矩阵Q由A的一组特征向量构成，即;
Q=[x_1,x_2,\cdots,x_n]
不妨把[x_1,x_2,\cdots,x_n]作为一组正交基，因此特征向量x可用这组正交基表示：
x=[x_1,x_2,\cdots,x_n][a_1,a_2,\cdots,a_n ]^T

由式（6.3）可得：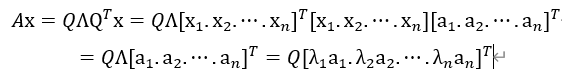

我们可以以2x2矩阵为例，把这个过程用几何图形表示如下：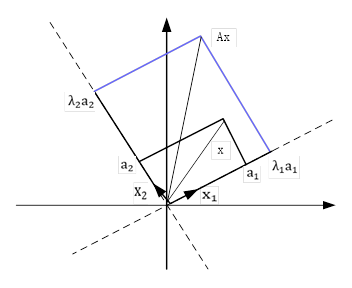

整个变换过程中，矩阵A特征值分解的本质是把向量x由一组正交基映射到另一组正交基上。
由此我们得到启发，对于一般矩阵A，其形状为mxn，如果能实现这个过程，是否也可以进
行类似于特征值分解？为此，我们假设n为空间已找到一组正交交基:
[v_1,v_2,\cdots,v_n]
矩阵A把这组正交基映射为：
[Av_1,Av_2,\cdots,Av_n]
如果要使映射后的这组向量成为一组正交向量，则需要满足如下条件，当i≠j时
由此可得：

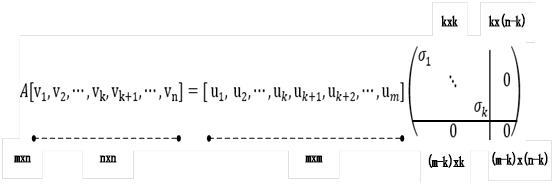
6.2.3 SVD的简单实例

例1: 设A=\left(\begin{matrix}0&1 \\ 1&1\\ 1&0\end{matrix}\right),对矩阵A进行奇异值分
解：
对角矩阵\sum=\left(\begin{matrix}\sqrt{3}&0 \\ 0&1\\ 0&0\end{matrix}\right)
可以验证
U\sum V^T=A
SVD分解矩阵A的步骤
(1) 求AA^T的特征值和特征向量，用单位化的特征向量构成 U。
(2) 求A^TA的特征值和特征向量，用单位化的特征向量构成 V。
(3) 将AA^T或者A^TA的特征值求平方根，然后构成 Σ。
3）用python实现这个实例

打印结果：
A: [[0 1]
[1 1]
[1 0]]
U: [[-4.08248290e-01 7.07106781e-01 5.77350269e-01]
[-8.16496581e-01 7.45552182e-17 -5.77350269e-01]
[-4.08248290e-01 -7.07106781e-01 5.77350269e-01]]
V: [[-0.70710678 -0.70710678]
[-0.70710678 0.70710678]]
d: [1.73205081 1. ]
进行还原

运行结果
P*D*Q: [[ 1.02120423e-16 1.00000000e+00]
[ 1.00000000e+00 1.00000000e+00]
[ 1.00000000e+00 -2.11898069e-16]]

奇异值分解函数：
np.linalg.svd(a, full_matrices=True, compute_uv=True, hermitian=False)
参数说明：
a : 是一个形如(M,N)矩阵
full_matrices：的取值是为False或者True，默认值为True，这时u的大小为(M,M)，vh的大小为(N,N) 。否则u的大小为(M,K)，vh的大小为(K,N) ，K=min(M,N)。
compute_uv：取值是为False或者True，默认值为True，表示计算u,s,vh。为0的时候只计算s
hermitian：如果为 True，则假定 a 为 Hermitian(如果为实值，则为对称)，从而可以更有效地找到奇异值。默认为False
返回值：
u： { (…, M, M), (…, M, K) } 数组
s： (…, K) 数组
vh： { (…, N, N), (…, K, N) } 数组
其中s是对矩阵a的奇异值分解。s除了对角元素不为0，其他元素都为0，并且对角元素从大到小排列。
s中有n个奇异值，一般排在后面的比较接近0，所以仅保留比较大的r个奇异值。

6.2.4 特征值的信息量如何度量？

在奇异值分解中，较大的奇异值会决定原矩阵的“主要特征”，如何根据A的奇异值分解来度量特征值的信息量。可以用矩阵A的F-范数的平方来
\left(||A||_F^2\right)衡量。
假设矩阵A的秩为k，矩阵U的前k个正交向量为[u_1,u_2,\cdots,u_k] ，矩阵V的前k个正交向量为[v_1,v_2,\cdots,v_k]，内积\left(\delta_i u_i v_i^T,\delta_j u_j v_j^T \right)=0,i\neq j
A=\sum_{i=1}^k \delta_i u_i v_i^T
||F||_F^2=\sum_{i=1}^k \delta_i^2
具体计算时一般选择前r\left(r\leq k\right)\delta_i^2之和与\left(||A||_F^2\right)的比是否达到一个值（如90%）。

6.2.5矩阵的近似表示

奇异值与特征值得意义类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。
A_{m\times n}=U_{m\times m}\sum_{m\times n} V_{n\times n}^T\approx U_{m\times k}\sum_{k\times k} V_{k\times n}^T
这个压缩或还原过程，用下图可表示更直观：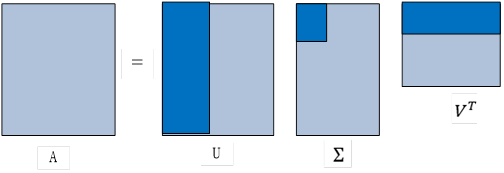
由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引。

6.2.6 SVD的改进算法

 数据方面的改进：
对数据进行规范化
 算法方面的改进：
SVD针对的矩阵A，很多是稀疏矩阵，其中有很多0，尤其在推荐需求的场景中。SVD通过过分依赖已有数据，这容易造成过拟合。为改进这个不足，人们开发出SVD的改进算法，
如RSVD、SVD++等等，大家有兴趣可参考相关论文。