第5 章机器学习基础(2/3) | Python技术交流与分享

文章目录

5.4 选择合适激活函数
5.5 选择合适的损失函数
5.6 使用合适的优化器
5.6.1传统梯度优化的不足
5.6.2 批量随机梯度下降法
5.6.3 动量算法
5.6.4 Nesterov动量算法
5.6.5 AdaGrad算法
5.6.6 RMSProp算法
5.6.7 Adam算法
5.6.8 Yogi算法
5.6.9 使用优化算法实例

5.4 选择合适激活函数

激活函数在神经网络中作用有很多，主要作用是给神经网络提供非线性建模能力。如果没有激活函数，那么再多层的神经网络也只能处理线性可分问题。作为神经网络的激活函数，一般需要如下3个条件。
1）非线性：为提高模型的学习能力，如果是线性，那么再多层都相当于只有两层效果。
2）可微性：有时可以弱化，在一些点存在偏导即可。
3）单调性：保证模型简单。
常用的激活函数有sigmoid、tanh、relu、softmax等。它们的图形、表达式、导数等信息如表5-2所示。
在搭建神经网络时，如何选择激活函数？如果搭建的神经网络层数不多，选择sigmoid、tanh、relu、softmax都可以；如果搭建的网络层次比较多，那就需要小心，选择不当就可导致梯度消失问题。此时一般不宜选择sigmoid、tanh激活函数，因它们的导数都小于1，尤其是sigmoid的导数在[0,1/4]之间，多层叠加后，根据微积分链式法则，随着层数增多，导数或偏导将指数级变小。所以层数较多的激活函数需要考虑其导数不宜小于1当然也不能大于1，大于1将导致梯度爆炸，导数为1最好，激活函数relu正好满足这个条件。所以，搭建比较深的神经网络时，一般使用relu激活函数，当然一般神经网络也可使用。此外，激活函数softmax由于 $\sum_i \delta_i(z)=1$ ,常用于多分类神经网络输出层。
激活函数在PyTorch中使用示例：

m = nn.Sigmoid()
input = torch.randn(2)
output = m(input)

m = nn.Sigmoid()

input = torch.randn(2)

output = m(input)

激活函数输入维度与输出维度是一样的。激活函数的输入维度一般包括批量数N,即输入数据的维度一般是4维，如(N,C,W,H)。

5.5 选择合适的损失函数

损失函数（Loss Function）在机器学习中非常重要，因为训练模型的过程实际就是优化损失函数的过程。损失函数对每个参数的偏导数就是梯度下降中提到的梯度，防止过拟合时添加的正则化项也是加在损失函数后面。损失函数用来衡量模型的好坏，损失函数越小说明模型和参数越符合训练样本。任何能够衡量模型预测值与真实值之间的差异的函数都可以叫做损失函数。在机器学习中常用的损失函数有两种，即交叉熵（Cross Entropy）和均方误差（Mean Squared Error，MSE），分别对应机器学习中的分类问题和回归问题。
对分类问题的损失函数一般采用交叉熵，交叉熵反应的两个概率分布的距离（不是欧氏距离）。分类问题进一步又可分为多目标分类，如一次要判断100张图是否包含10种动物，或单目标分类。
回归问题预测的不是类别，而是一个任意实数。在神经网络中一般只有一个输出节点，该输出值就是预测值。反应的预测值与实际值之间距离可以用欧氏距离来表示，所以对这类问题我们通常使用均方差作为损失函数，均方差的定义如下：
$MSE=\frac{\sum_{i=1}^n (y_i - y_{i}')^2}{n} \tag{5.8}$
PyTorch中已集成多种损失函数，这里介绍两个经典的损失函数，其他损失函数基本上是在它们的基础上的变种或延伸。
1.torch.nn.MSELoss
具体格式：

torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

1	torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')

计算公式：
$L(x,y)=(l_1,l_2,\cdots,l_N)^T,l_n=(x_n-y_n)^2$
其中，N是批量大小。
如果参数reduction为非None（默认值为'mean'），则：
$L(x,y)=\begin{cases} mean(L),if reduction='mean'\\ sum(L),if reduction='sum')\end{cases} \tag{5.9}$
x和y是任意形状的张量，每个张量都有n个元素，如果reduction取'none', L(x,y)将不是标量；如果取'sum', L(x,y)只是差平方的和，但不会除以n。
参数说明：
size_average，reduce在PyTorch官方的后续版本中将移除，主要看参数reduction，reduction可以取'none','mean','sum',默认值为'mean'。如果size_average，reduce取了值，将覆盖reduction的值。
代码示例：

import torch
import torch.nn as nn
import torch.nn.functional as F

torch.manual_seed(10)

loss = nn.MSELoss(reduction='mean')
input = torch.randn(1, 2, requires_grad=True)
print(input)
target = torch.randn(1, 2)
print(target)
output = loss(input, target)
print(output)
output.backward()

import torch

import torch.nn as nn

import torch.nn.functional as F

torch.manual_seed(10)

loss = nn.MSELoss(reduction='mean')

input = torch.randn(1, 2, requires_grad=True)

print(input)

target = torch.randn(1, 2)

print(target)

output = loss(input, target)

print(output)

output.backward()

2.torch.nn.CrossEntropyLoss
交叉熵损失（Cross-Entropy Loss）又称为对数似然损失（Log-likelihood Loss）、对数损失；二分类时还可称为逻辑斯谛回归损失（Logistic Loss）。在Pytroch里，它不是严格意义上的交叉熵损失函数，而是先将input经过softmax激活函数，将向量“归一化”成概率形式，然后再与target计算严格意义上的交叉熵损失。在多分类任务中，经常采用softmax激活函数+交叉熵损失函数，因为交叉熵描述了两个概率分布的差异，然而神经网络输出的是向量，并不是概率分布的形式。所以需要softmax激活函数将一个向量进行“归一化”成概率分布的形式，再采用交叉熵损失函数计算损失值。
一般格式：

torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

1	torch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

计算公式：
$loss(x,class)=-log(\frac {exp(x[class])}{(\sum_j exp(x[j]))})=-x[class]+log(\sum_j exp (x[j])) \tag{5.10}$
如果带上权重参数weight，则：
$loss(x,class)=weight[class](-x[class]+log(\sum_j exp(x[j])))\tag{5.11}$
weight(Tensor)- 为每个类别的loss设置权值，常用于类别不均衡问题。weight必须是float类型的tensor，其长度要于类别C一致，即每一个类别都要设置有weight。
代码示例：

import torch
import torch.nn as nn

torch.manual_seed(10)

loss = nn.CrossEntropyLoss()
#假设类别数为5
input = torch.randn(3, 5, requires_grad=True)
#每个样本对应的类别索引,其值范围为[0,4]
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()

import torch

import torch.nn as nn

torch.manual_seed(10)

loss = nn.CrossEntropyLoss()

#假设类别数为5

input = torch.randn(3, 5, requires_grad=True)

#每个样本对应的类别索引,其值范围为[0,4]

target = torch.empty(3, dtype=torch.long).random_(5)

output = loss(input, target)

output.backward()

5.6 使用合适的优化器

优化器在机器学习、深度学习中往往起着举足轻重的作用，同一个模型，因选择不同的优化器，性能有可能相差很大，甚至导致一些模型无法训练。所以，了解各种优化器的基本原理非常必要。本节重点介绍各种优化器或算法的主要原理，及各自的优点或不足。

5.6.1传统梯度优化的不足

传统梯度更新算法为最常见、最简单的一种参数更新策略。其基本思想是：先设定一个学习率 $\lambda$ ，参数沿梯度的反方向移动。假设基于损失函数 $L(f(x,\theta),y)$ ，其中 $\theta$ 需更新的参数，梯度为g，则其更新策略的伪代码如下所示：

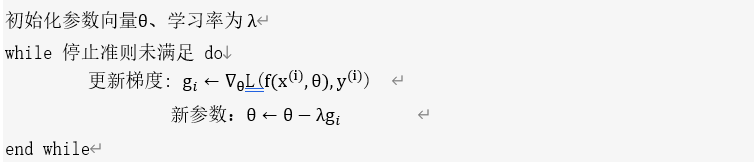
这种梯度更新算法简洁，当学习率取值恰当时，可以收敛到全面最优点（凸函数）或局部最优点（非凸函数）。
但其不足也很明显，对超参数学习率比较敏感（过小导致收敛速度过慢，过大又越过极值点），如图5-12的右图所示。在比较平坦的区域，因梯度接近于0，易导致提前终止训练，如图5-12的左图所示，要选中一个恰当的学习速率往往要花费不少时间。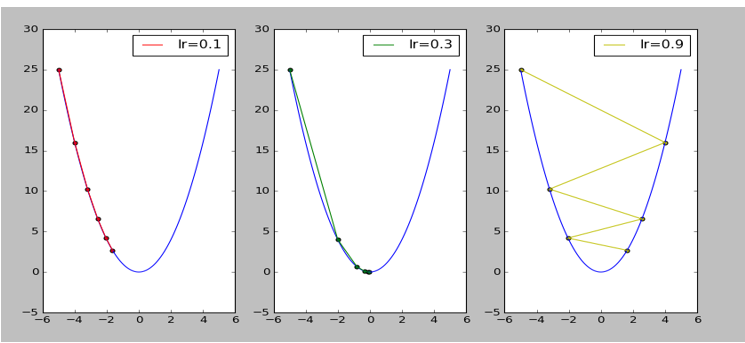
图5-12学习速率对梯度的影响
学习率除了敏感，有时还会因其在迭代过程中保持不变，很容易造成算法被卡在鞍点的位置，如图5-13所示。

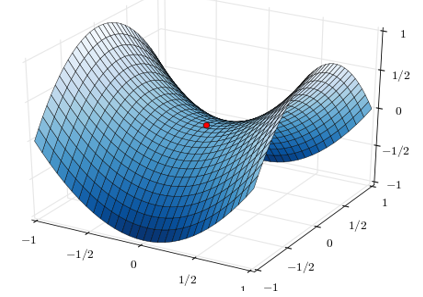
图5-13算法卡在鞍点示意图
另外，在较平坦的区域，因梯度接近于0，优化算法往往因误判，还未到达极值点，就提前结束迭代，如图5-14所示。

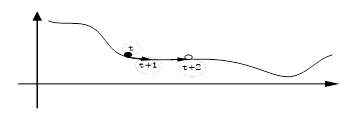
图5-14在较平坦区域，梯度接近于0，优化算法因误判而提前终止迭代
传统梯度优化方面的这些不足，在深度学习中会更加明显。为此，人们自然想到如何克服这些不足的问题。从本小节前文更新策略的伪代码可知，影响优化的主要因素有：
• 优化训练数据集的大小
• 优化梯度方向
• 优化学习率
所以很多优化方法大多从这些方面入手，数据集优化方面采用批量随机梯度下降方法，从梯度方向优化方面有动量更新策略；有些从学习率入手，这涉及自适应问题；还有从两方面同时入手等方法，接下来将介绍这些方法。

5.6.2 批量随机梯度下降法

梯度下降法是非常经典的算法，训练时，如果使用全训练集，虽然可获得较稳定的值，但比较耗费资源，尤其当训练数据比较大时；另一个极端时，每次训练时用一个样本（又称为随机梯度下降法），这种训练方法振幅较大，也比较耗时，如图5-15所示。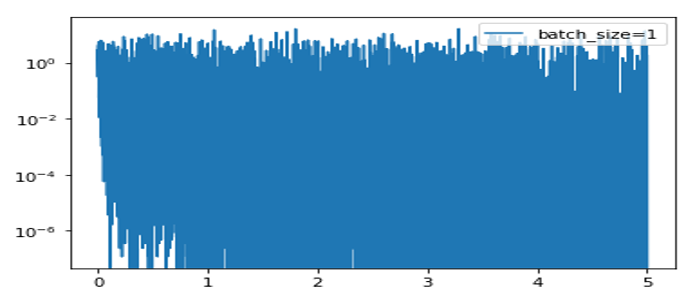
图5-15 随机梯度下降法的损失值变化示意图
这种方法虽然资源消耗较少，但很耗时时间，因这种方法无法充分发挥深度学习程序库中高度优化的矩阵运算的优势。为更有效训练模型，我们采用一种折中方法，即批量随机下降法。这种梯度下降方法有两个特点：一是批量，另一个是随机性。如何实现批量随机下降呢？其伪代码如下：
其中 $x^{(i)}$ 和小批量数据集的所有元素都是从训练集中随机抽出的，这样梯度的预期将保持不变，相对于随机梯度下降，批量随机梯度下降降低了收敛波动性，即降低了参数更新的方差，使得更新更加稳定，这些因素都有利于提升其收敛效果，如图5-16所示。
图5-16 批量随机梯度下降法的损失值变化示意图

5.6.3 动量算法

梯度下降法在遇到平坦或高曲率区域时，学习过程有时很慢。利用动量算法能比较好解决这个问题。动量算法与传统梯度下降优化的效果，我们以求解函数 $f(x_1,x_2)=0.05x_1^2+2x_1^2$ 极值为例，使用梯度下降法和动量算法分别进行迭代求解，具体迭代过程如图5-17、图5-18所示（图实现代码请参考本书第5章代码部分）。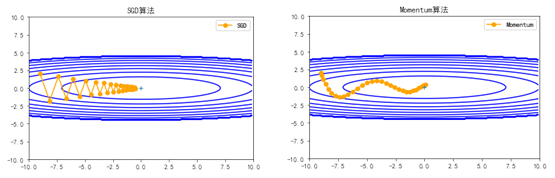
图5-17 梯度下降法的迭代轨迹图5-18 使用动量项的迭代轨迹
从图5-17 可以看出，不使用动量算法的SGD学习速度比较慢，振幅比较大；图5-18 可以看出，使用动量算法的SGD,振幅较小，而且较快到达极值点。动量算法是如何做到这点的呢？
动量（momentum）是模拟物理里动量的概念，具有物理上惯性的含义，一个物体在运动时具有惯性，把这个思想运用到梯度下降计算中，可以增加算法的收敛速度和稳定性，具体实现如图5-19所示。

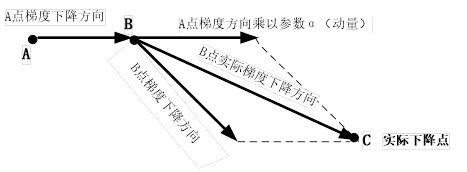
图5-19动量算法示意图
由图5-19所示，可知动量算法每下降一步都是由前面下降方向的一个累积和当前点的梯度方向组合而成。含动量的随机梯度下降法，其算法伪代码如下：
批量随机梯度下降法PyTorch代码实现：

def sgd_momentum(parameters, vs, lr, gamma):
    for param, v in zip(parameters, vs):
        v[:] = gamma * v + lr * param.grad
        param.data -= v
        param.grad.data.zero_()

def sgd_momentum(parameters, vs, lr, gamma):

for param, v in zip(parameters, vs):

v[:] = gamma * v + lr * param.grad

param.data -= v

param.grad.data.zero_()

其中parameters是模型参数，假设模型为model，则parameters指model. parameters()。
具体使用动量算法时，动量项的计算公式如下：
$v_k=\alpha v_{k-1}+(-\lambda \hat g(\theta_k)\tag{5.12}$
如果按时间展开，则第k次迭代使用了从1到k次迭代的所有负梯度值，且负梯度按动量系数α指数级衰减，相当于使用了移动指数加权平均，具体展开过程如下：
由此可知，当在比较平缓处，但α=0.5、0.9时，将是分别是梯度下降法的2倍、10倍。
使用动量算法，不但可加速迭代速度，还可能跨过局部最优找到全局最优，如图5-20所示。
图5-20 使用动量算法的潜在优势

5.6.4 Nesterov动量算法

既然每一步都要将两个梯度方向（历史梯度、当前梯度）做一个合并再下降，那为什么不先按照历史梯度往前走那么一小步，按照前面一小步位置的“超前梯度”来做梯度合并呢？如此一来，可以先往前走一步，在靠前一点的位置（如图5-21中的C点）看到梯度，然后按照那个位置再来修正这一步的梯度方向，如图5-21所示。

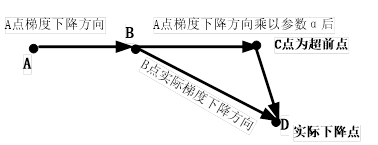
图5-21 Nesterov下降法示意图
这就得到动量算法的一种改进算法，称为NAG（Nesterov Accelerated Gradient）算法，也称Nesterov动量算法。这种预更新方法能防止大幅振荡，不会错过最小值，并对参数更新更加敏感。如图5-22所示。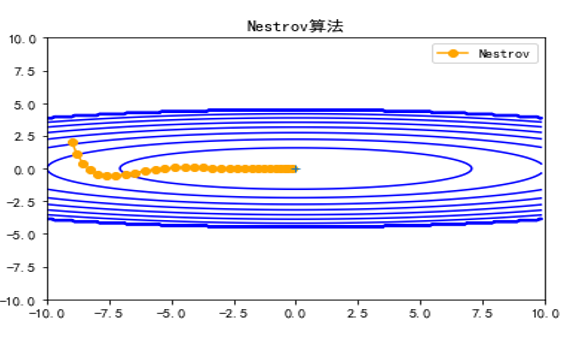
图5-22 Nesterov加速梯度下降法
NAG下降法的算法伪代码如下：

NAG算法的PyTorch实现如下：

def sgd_nag(parameters, vs, lr, gamma):
    for param, v in zip(parameters, vs):
        v[:]*= gamma
        v[:]-= lr * param.grad
        param.data += gamma * gamma * v
        param.data -= (1 + gamma) * lr * param.grad
        param.grad.data.zero_()

def sgd_nag(parameters, vs, lr, gamma):

for param, v in zip(parameters, vs):

v[:]*= gamma

v[:]-= lr * param.grad

param.data += gamma * gamma * v

param.data -= (1 + gamma) * lr * param.grad

param.grad.data.zero_()

NAG动量法和经典动量法的差别就在B点和C点梯度的不同。动量法，更多关注梯度下降方法的优化，如果能从方向和学习率同时优化，效果或许更理想。事实也确实如此，而且这些优化在深度学习中显得尤为重要。接下来我们介绍几种自适应优化算法，这些算法同时从梯度方向及学习率进行优化，效果非常好。

5.6.5 AdaGrad算法

传统梯度下降算法对学习率这个超参数非常敏感，难以驾驭；对参数空间的某些方向也没有很好的方法。这些不足在深度学习中，因高维空间、多层神经网络等因素，常会出现平坦、鞍点、悬崖等问题，因此，传统梯度下降法在深度学习中显得力不从心。还好现在已有很多解决这些问题的有效方法。上节介绍的动量算法在一定程度缓解对参数空间某些方向的问题，但需要新增一个参数，而且对学习率的控制还不很理想。为了更好驾驭这个超参数，人们想出来多种自适应优化算法，使用自适应优化算法，学习率不再是一个固定不变值，它会根据不同情况自动调整来适用情况。这些算法使深度学习向前迈出一大步！这节我们将介绍几种自适应优化算法。
AdaGrad算法是通过参数来调整合适的学习率λ，能独立地自动调整模型参数的学习率，对稀疏参数进行大幅更新和对频繁参数进行小幅更新，如图5-23所示。因此，Adagrad方法非常适合处理稀疏数据。AdaGrad算法在某些深度学习模型上效果不错。但还有些不足，可能因其累积梯度平方导致学习率过早或过量的减少所致。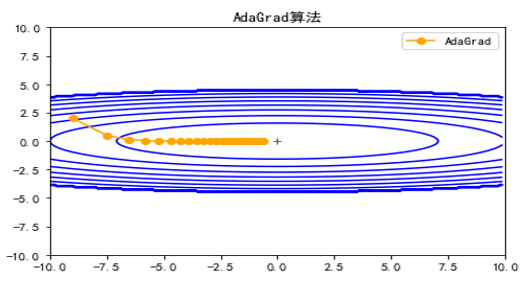
图5-23 AdaGrad 算法迭代过程示意图
AdaGrad算法伪代码如下：
由上面算法的伪代码可知：
•随着迭代时间越长，累积梯度r越大，从而学习速率 $\frac{\lambda}{\delta+\sqrt{r}}$ 随着时间就减小，在接近目标值时，不会因为学习速率过大而越过极值点。
•不同参数之间学习速率不同，因此，与前面固定学习速率相比，不容易在鞍点卡住。
•如果梯度累积参数r比较小，则学习速率会比较大，所以参数迭代的步长就会比较大。相反，如果梯度累积参数比较大，则学习速率会比较小，所以迭代的步长会比较小。
AdaGrad算法的PyTorch实现代码：

def sgd_adagrad(parameters, s, lr):
    eps = 1e-10
    for param, s in zip(parameters, s):
        s[:] = s + (param.grad) ** 2
        div = lr / torch.sqrt(s + eps) * param.grad
        param.data = param.data - div
        param.grad.data.zero_()

def sgd_adagrad(parameters, s, lr):

eps = 1e-10

for param, s in zip(parameters, s):

s[:] = s + (param.grad) ** 2

div = lr / torch.sqrt(s + eps) * param.grad

param.data = param.data - div

param.grad.data.zero_()

5.6.6 RMSProp算法

RMSProp算法修改AdaGrad，为的是在非凸背景下的效果更好，在凸函数可能振幅较大，如图5-24所示。对梯度平方和累计越来越大的问题，RMSProp指数加权的移动平均代替梯度平方和。RMSProp为使用移动平均，引入了一个新的超参数ρ，用来控制移动平均的长度范围。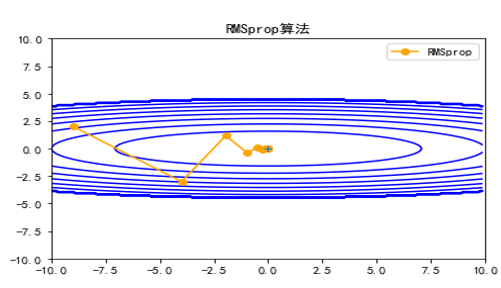
图5-24 RMSProp迭代过程示意图
RMSProp算法伪代码如下：
RMSProp算法在实践中已被证明是一种有效且实用的深度神经网络优化算法，在深度学习中得到广泛应用。
RMSProp算法PyTorch实现代码如下：

def rmsprop(parameters, s, lr, alpha):
    eps = 1e-10
    for param, sqr in zip(parameters, s):
        sqr[:] = alpha * sqr + (1 - alpha) * param.grad ** 2
        div = lr / torch.sqrt(sqr + eps) * param.grad
        param.data = param.data - div
        param.grad.data.zero_()

def rmsprop(parameters, s, lr, alpha):

eps = 1e-10

for param, sqr in zip(parameters, s):

sqr[:] = alpha * sqr + (1 - alpha) * param.grad ** 2

div = lr / torch.sqrt(sqr + eps) * param.grad

param.data = param.data - div

param.grad.data.zero_()

5.6.7 Adam算法

Adam（Adaptive Moment Estimation，自适应矩估计）算法本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳，如图5-25所示。
图5-25 Adam算法迭代过程示意图
Adam算法是另一种学习速率自适应的深度神经网络方法，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习速率。Adam算法伪代码如下：
Adam算法的PyTorch实现如下。

def adam(parameters, vs, s, lr, t, beta1=0.9, beta2=0.999):
    eps = 1e-8
    for param, v, sqr in zip(parameters, vs, s):
        v[:] = beta1 * v + (1 - beta1) * param.grad
        sqr[:] = beta2 * sqr + (1 - beta2) * param.grad ** 2
        v_hat = v / (1 - beta1 ** t)
        s_hat = sqr / (1 - beta2 ** t)
        param.data = param.data - lr * v_hat / (torch.sqrt(s_hat) + eps)
        param.grad.data.zero_()

def adam(parameters, vs, s, lr, t, beta1=0.9, beta2=0.999):

eps = 1e-8

for param, v, sqr in zip(parameters, vs, s):

v[:] = beta1 * v + (1 - beta1) * param.grad

sqr[:] = beta2 * sqr + (1 - beta2) * param.grad ** 2

v_hat = v / (1 - beta1 ** t)

s_hat = sqr / (1 - beta2 ** t)

param.data = param.data - lr * v_hat / (torch.sqrt(s_hat) + eps)

param.grad.data.zero_()

5.6.8 Yogi算法

Adam算法综合了动量算法及自适应算法的优点，是深度学习常用的算法，但也存在一些问题：即使在凸环境下，当 r的第二力矩估计值爆炸时，它可能无法收敛。为此可通过改进r和优化参数初始化等方法来解决。其中通过改进r是一种有效方法，即把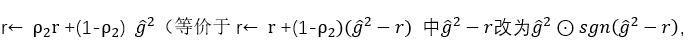
这就是Yogi更新。
Yogi算法的PyTorch代码如下：

def yogi(parameters, vs, s, lr, t, beta1=0.9, beta2=0.999):
    eps = 1e-8
    for param, v, sqr in zip(parameters, vs, s):
        v[:] = beta1 * v + (1 - beta1) * param.grad
        #sqr[:] = beta2 * sqr + (1 - beta2) * param.grad ** 2
        sqr[:] = sqr + (1 - beta2) * torch.sign(torch.square(param.grad) - sqr) * torch.square(param.grad)
        v_hat = v / (1 - beta1 ** t)
        s_hat = sqr / (1 - beta2 ** t)
        param.data = param.data - lr * v_hat / (torch.sqrt(s_hat) + eps)
        param.grad.data.zero_()

def yogi(parameters, vs, s, lr, t, beta1=0.9, beta2=0.999):

eps = 1e-8

for param, v, sqr in zip(parameters, vs, s):

v[:] = beta1 * v + (1 - beta1) * param.grad

#sqr[:] = beta2 * sqr + (1 - beta2) * param.grad ** 2

sqr[:] = sqr + (1 - beta2) * torch.sign(torch.square(param.grad) - sqr) * torch.square(param.grad)

v_hat = v / (1 - beta1 ** t)

s_hat = sqr / (1 - beta2 ** t)

param.data = param.data - lr * v_hat / (torch.sqrt(s_hat) + eps)

param.grad.data.zero_()

前文介绍了深度学习的正则化方法，它是深度学习核心之一；优化算法也是深度学习的核心之一。优化算法很多，如随机梯度下降法、自适应优化算法等，那么具体使用时该如何选择呢？
RMSprop、Nesterov、Adadelta和Adam被认为是自适应优化算法，因为它们会自动更新学习率。而使用SGD时，必须手动选择学习率和动量参数，通常会随着时间的推移而降低学习率。
有时可以考虑综合使用这些优化算法，如采用先用Adam，然后用SGD优化方法，这个想法，实际上由于在训练的早期阶段SGD对参数调整和初始化非常敏感。因此，我们可以通过先使用Adam优化算法进行训练，这将大大节省训练时间，且不必担心初始化和参数调整，一旦用Adam训练获得较好的参数后，我们可以切换到SGD +动量优化，以达到最佳性能。采用这种方法有时能达到很好效果，如图5-26所示，迭代次数超过150后，用SGD效果好于Adam。
图5-26 迭代次数与测试误差间的对应关系

5.6.9 使用优化算法实例

这里使用MNIST数据集，使用自定义的优化算法实现图像的分类任务。为便于比较这里使用梯度下降法及动量算法两种优化算法。数据集的导入及预处理可参考本书的3.5节或参考本书第5章对应代码。
1）算法定义。可参考本书第5.6.2和5.6.3节中PyTorch实现算法部分。
2）定义模型。

net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

net = nn.Sequential(

nn.Linear(784, 200),

nn.ReLU(),

nn.Linear(200, 10),

)

3）定义损失函数。

loss_sgd = nn.CrossEntropyLoss()

1	loss_sgd = nn.CrossEntropyLoss()

4）加载数据。这里使用批量大小为128的训练数据集。

train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)

1	train_loader = DataLoader(train_dataset, batch_size=128, shuffle=True)

5）训练模型。

# 初始化梯度平方项
s = []
for param in net.parameters():
    s.append(torch.zeros_like(param.data))

# 开始训练
losses0 = []
idx = 0

start = time.time() # 记时开始
for e in range(5):
    train_loss = 0
    for img, label in train_loader:
        #展平img
        img=img.view(img.size(0),-1)
        # 正向传播
        out = net(img)
        loss = loss_sgd(out, label)
        # 反向传播
        net.zero_grad()
        loss.backward()
        sgd(net.parameters(),1e-2)
        # 记录误差
        train_loss += loss.item()
        if idx % 30 == 0:
            losses0.append(loss.item())
        idx += 1
    print('epoch: {}, Train Loss: {:.6f}'.format(e, train_loss / len(train_loader)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

# 初始化梯度平方项

s = []

for param in net.parameters():

s.append(torch.zeros_like(param.data))

# 开始训练

losses0 = []

idx = 0

start = time.time() # 记时开始

for e in range(5):

train_loss = 0

for img, label in train_loader:

#展平img

img=img.view(img.size(0),-1)

# 正向传播

out = net(img)

loss = loss_sgd(out, label)

# 反向传播

net.zero_grad()

loss.backward()

sgd(net.parameters(),1e-2)

# 记录误差

train_loss += loss.item()

if idx % 30 == 0:

losses0.append(loss.item())

idx += 1

print('epoch: {}, Train Loss: {:.6f}'.format(e, train_loss / len(train_loader)))

end = time.time() # 计时结束

print('使用时间: {:.5f} s'.format(end - start))

如果使用动量算法，只要把sgd(net.parameters(),1e-2)改为sgd_momentum(net.parameters(), vs, 1e-2, 0.9)即可。
6）可视化两种优化算法的运行结果。

x_axis = np.linspace(0, 5, len(losses0), endpoint=True)
plt.semilogy(x_axis, losses0, label='sgd')
plt.semilogy(x_axis, losses1, label='momentum')
plt.legend(loc='best')

x_axis = np.linspace(0, 5, len(losses0), endpoint=True)

plt.semilogy(x_axis, losses0, label='sgd')

plt.semilogy(x_axis, losses1, label='momentum')

plt.legend(loc='best')

运行结果如图5-27所示。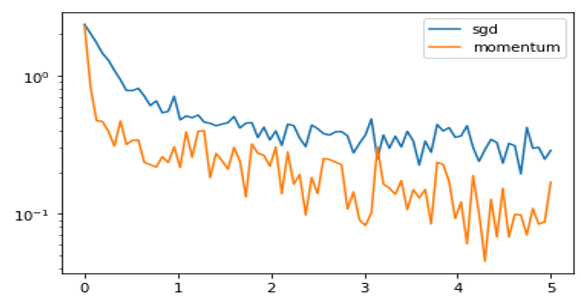
图5-27 梯度下降法与动量算法的比较
从图5-27可知，动量算法的优势还是非常明显的。完整代码及其他优化算法的实现请参考本书第5章的代码及数据部分。