1.10泰勒公式

如果一个复杂函数在某点处存在各阶导数，在这点附近，就可以用一个多项式函数，近似地替代这个复杂函数。这种化繁为简的功能就是泰勒公式的本质和意义所在。
如何用多项式函数近似表示这个复杂函数呢？根据微分的定义，如果函数f(x)在点a处可得，可用一次函数近似代替函数f(x)，误差是x-a的高阶无穷小。
f(x)=f(a)+f'(a)(x-a)+o(x-a)
由此，我们可以推广到更高次阶的情况。假设函数f(x)n阶可导，函数f(x)可表示为：
f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!} (x-a)^n+o(x-a)^n \tag{5.5}
这就是泰勒多项式，其中o(x-a)^n称为皮亚诺余项。
如果令\Delta x=x-a，式（5.5）可写成：
f(x)=f(a)+f'(a)\Delta x+\frac{f''(a)}{2!}\Delta x^2+\cdots+\frac{f^{(n)}(a)}{n!} \Delta x^n+o(\Delta x)^n
函数在x=0点处的泰勒公式称为麦克劳林公式，具体形式为：
f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!} x^n+o(x^n) \tag{5.6}
把余项o(x^n)记为R_n (x),式（5.6）可写为：
f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!} x^n+R_n (x) \tag{5.7}
基本函数的麦克劳林公式：

用泰勒公式近似sinx函数，分别取k=3,5的情况

 
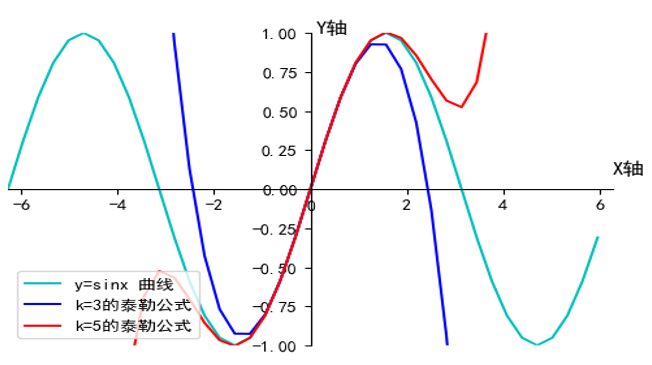
从上图可以看出，泰勒公式精度随着k增大而精度越高。
实现上图的python代码：

利用泰勒公式可以将非线性问题化为线性问题，且具有很高的精确度，因此其在微积分的各个方面都有重要的应用，如用于梯度下降法、牛顿法、拟牛顿法等的推导。