1.9 导数与函数极值

费马定理给出了极值的必要条件，如何给出充分条件？这节将介绍导数与极值的关系，从而给出函数极值的几个充分条件。当然，讲到极值就离不开最大和最小值，极值一般指函数的局部属性，而最大值与最小值反映了函数一种整体属性．本节主要讨论极值与最大值、最小值的判定和求法。
极值定义:设函数y=f(x)在点 $x_0$ 的 $\delta$ 领域内有定义，如果对去心领域内任何一点x都有 $f(x_0 )\le f(x)$ (或 $f(x_0 )\ge f(x))$ ，则称 $f(x_0)$ 是函数f(x)的极小值，或为极大值。
函数的极大值与极小值统称为函数的极值，使函数取得极值的点称为极值点。
如何判断一点是否为函数的极值点？费马定理只给出了极值点的必要条件，极值点的充分条件如何呢？这里介绍一种使用导数来判断是否极值的方法。
1）利用一阶导数
设函数f(x)在点 $x_0$ 连续，在点 $x_0$ 的某去心领域可导。
如 $x\in(x_0-\delta,x_0),f'(x)<0; x\in(x_0,x_0+\delta),f'(x)>0,$ 则函数f(x)在点 $x_0$ 处取得极小值；
如 $x\in(x_0-\delta,x_0),f'(x)>0; x\in(x_0,x_0+\delta),f'(x)<0,$ 则函数f(x)在点 $x_0$ 处取得极大值；
如 $x\in(x_0-\delta,x_0),or x\in(x_0,x_0+\delta),f'(x)$ 符合保持不变,则函数f(x)在点 $x_0$ 处没有极值。
2）利用二阶导数
设函数f(x)在点 $x_0$ 处二阶可导，且 $x_0$ 为驻点（即 $f'(x_0 )=0)$ 。
如 $f''(x_0 )<0,$ 则函数f(x)在点 $x_0$ 处取得极大值；如 $f''(x_0 )>0,$ 则函数f(x)在点 $x_0$ 处取得极小值；
如 $f''(x_0 )=0,$ 则函数f(x)在点 $x_0$ 不一定取得极值，需进一步分析。
驻点、拐点、极值点、鞍点的异同（这里的函数为一元函数）

例1：判断下列函数在x=0处的情况
$y=10x^2,y=10x^3$
解：
这两个函数的图像为：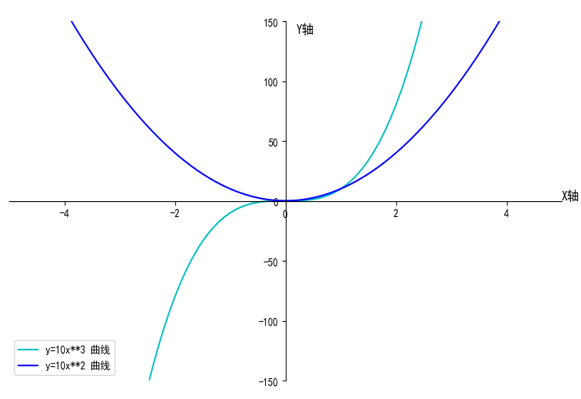
从图可知：