第3章 偏导数与矩阵
3.1.黑塞矩阵
费马定理给出了多元函数极值的必要条件,黑塞矩阵的正定性是极值的充分条件。此外,黑塞矩阵与多元函数的极值、凹凸性有密切的关系。
黑塞矩阵是由多元函数的二阶偏导数组成的矩阵,假设函数 二阶可导,黑塞矩阵由所有二阶偏导数构成,函数
二阶可导,黑塞矩阵由所有二阶偏导数构成,函数 的黑塞矩阵定义为:
的黑塞矩阵定义为:

这是一个n阶矩阵,一般情况下,多元函数的混合二阶偏导数与次序无关,即:

因此,黑塞矩阵是一个对称矩阵。
费马引理给出了多元函数极值的必要条件,极值的充分条件由黑塞矩阵的正定性决定。
例1:求函数 的黑塞矩阵。
的黑塞矩阵。
函数f的黑塞矩阵为:

练习:
求函数 对应的黑塞矩阵。
对应的黑塞矩阵。
3.2 凹凸性判别法则
一元函数的凹凸性定义可以推广到多元函数,即:对于函数f(x),在其定义域内的任意两点x和y,及任意实数 ,都有:
,都有:

则函数f(x)为凸函数,反之,为凹函数。
函数 是凸函数,
是凸函数, 为凹函数。它们对应图像如下:
为凹函数。它们对应图像如下:
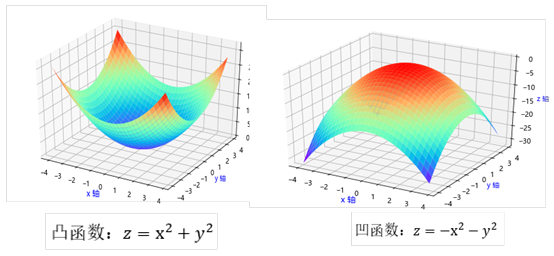
一元函数的凹凸性可根据二阶导数判断,多元函数可根据对应的黑塞矩阵的判断:
即:假设多元函数f(x)二阶可导,如果对应的黑塞矩阵半正定,则函数f(x)是凸函数;
如果对应的黑塞矩阵负正定,则函数f(x)是凹函数。
3.3 极值判别法则
一元函数的极值点的必要条件是该点为驻点,充分条件通过二阶导数来判断。这些规则可以推广到多元函数。多元函数的极值点的必要条件是该点为驻点,充分条件通过对应黑塞矩阵
来判断。具体规则如下:
(1)黑塞矩阵正定,函数在该点有极小值;
(2)黑塞矩阵负定,函数在该点有极大值;
(3)黑塞矩阵不定,则该点不是极值点,或是鞍点。
3.4雅可比矩阵
雅可比矩阵是由多个多元函数的所有偏导数构成的矩阵。假设:

由这些函数构成的雅可比矩阵为:

这是一个 的矩阵,每一行为一个多元函数的梯度(或所有偏导数)。
的矩阵,每一行为一个多元函数的梯度(或所有偏导数)。
例2:求下列函数的雅可比矩阵:


这些函数的雅可比矩阵为:

神经网络中通常包括多个多元函数的情况,如下图所示:
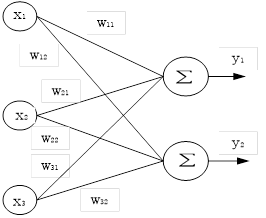
设
上图可用如下表达式表示:

由此可得:

【延伸思考】对 加上激活函数(如sigmoid函数),此时
加上激活函数(如sigmoid函数),此时
3.5 链式法则的矩阵形式
前面我们介绍了雅可比矩阵,它是涉及多元复合函数求导,这里雅可比矩阵可以简化链式法则的表达形式。
假设
根据链式法则,z对x的偏导可以通过z对 求导,
求导, 对x求导来实现。具体计算过程如下:
对x求导来实现。具体计算过程如下:

写成矩阵的形式就是: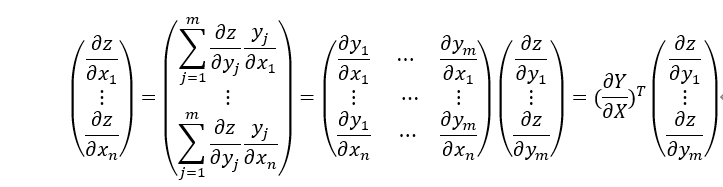
其中 矩阵就是雅可比矩阵。
矩阵就是雅可比矩阵。
3.6 对向量和矩阵求导
在神经网络中我们常见如下表达式:
y=Wx
其中W为mxn矩阵,x是n维向量,y是m维向量。假设f为一个激活函数,y通过激活函数后为f(y)函数,现在对f(y)求导,激活函数不改变y的维度,所以f(y)也是m维向量。
根据链式法则,有:

用矩阵和向量表示,上式可简写为:

3.7 应用:最小二乘法
最小二乘法(二乘”就是平方,所以又称最小平方法)是一种数学优化技术。 它通过最小化误差的平方(即通常我们称之为损失函数)和寻找数据的最佳函数匹配。 利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。为解决过拟合问题可以在损失函数后加上正则项。
对多元函数的最小二乘法,可以用矩阵或向量表示,如对线性回归的函数 ,其中w和b为参数。如果用向量或矩阵来表示,可先作如下处理:
,其中w和b为参数。如果用向量或矩阵来表示,可先作如下处理:
W=[w,b],X=[x,1]
则wx+b可表示为: ,目标函数可表示为:
,目标函数可表示为:

其中N表示样本总数, 表示第i个样本对应的标签值(或实际值)。L(w)
表示第i个样本对应的标签值(或实际值)。L(w)
是一个凸函数,可用最小二乘法求其最小值:
(1)对函数L(w)求一阶偏导

其中 表示第k个样本的第i个分量。
表示第k个样本的第i个分量。
(2)求二阶偏导,得到黑塞矩阵

由此可得,目标函数的黑塞矩阵为:
其中n表示向量W的维度(或长度)。
(3)证明黑塞矩阵的正定性
对任意非0向量x有:

故目标函数的黑塞矩阵为正定矩阵,由此可知,目标函数为凸函数,故存在极小值。驻点就是极值点。
(4)求解参数w
目标函数对参数w求导,并令导数为0,解得极值点。
由式(3.1)可得:

把 展开为:
展开为: ,从而有:
,从而有:

对上式进行整理可得:

写成矩阵的形式可得:

如果W的系数矩阵 可逆,则可解得方程组的解w为:
可逆,则可解得方程组的解w为:

如果w的维度和样本数较大,这种计算非常好资源,尤其当 不可逆,该如何求呢?
不可逆,该如何求呢?
对这些情况,我们可以采用梯度下降,通过不断迭代,最后收敛于极值点来实现。