文章目录
第4章 梯度
偏导数是对一个变量求导,它只反应函数与一个自变量之间的关系,无法反应所有自变量与函数的关系。梯度则连接函数所有自变量的导数,综合了对所有自变量的关系,对单变量而言,梯度就是微分;对多变量函数而言,它是多元函数对多个自变量偏导数形成的向量。
4.1 单变量函数的梯度
对单变量函数(如 ),其微分就是梯度,梯度通常用倒三角(
),其微分就是梯度,梯度通常用倒三角( )表示:
)表示:
如函数f(x)在点x处的梯度,可表示为

函数f(x)在点x的梯度就是函数在该点的切线斜率。
4.2 多变量函数的梯度
多变量函数(如 )的梯度
)的梯度
对多变量函数,如 ,则函数y的梯度是对所有自变量的偏导数构成的向量,表示如下:
,则函数y的梯度是对所有自变量的偏导数构成的向量,表示如下:
![\nabla f(x)=[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f3c73e2ee602059c209f5ea00ecb2a0c.gif)
梯度的方向就是函数给定点上升最快的方向,梯度的反方向是函数在给定点下降最快的方向。
梯度有什么作用呢?它是寻找函数极值的重要依据,下节将详细介绍。
4.3梯度与梯度直方图(HOG)
图像的梯度(x和y导数)非常有用,因为边缘和拐角(强度突变的区域)周围的梯度幅度很大,并且边缘和拐角比平坦区域包含更多关于物体形状的信息。
方向梯度直方图(Histogram of Oriented Gradient,HOG)
4.3.1图像梯度
梯度的方向是函数 f(x,y) 变化最快的方向,当图像中存在边缘时,有一些相邻像素的灰度值变化比较大,即一定有较大的梯度值。所以可以求图像的梯度来确定图像的边缘。
图像梯度是指图像某像素在x和y两个方向上的变化率(与相邻像素比较),是一个二维向量,由2个分量组成,X轴的变化、Y轴的变化 。
其中X轴的变化是指当前像素右侧(X加1)的像素值减去当前像素左侧(X减1)的像素值,如下图所示:

同理,Y轴的变化是当前像素下方(Y加1)的像素值减去当前像素上方(Y减1)的像素值。
计算出来这2个分量,形成一个二维向量,就得到了该像素的图像梯度。
分别对图像按照x方向和y方向进行求偏导,得到x梯度图和y梯度图。
导数的含义就是计算像素灰度值的变化率,对于离散图像而言,在图像上使用一阶差分来计算相邻像素之间的差值,从而得到图像的梯度。
下面这个公式表示了图像的梯度:

梯度是矢量,存在幅值和方向。
梯度的幅值(magnitude)为:

如果g大于某阈值,则认为该点(x,y)为边缘点。
梯度的方向(direction)为:

也可以使用二阶差分求梯度:


下面为一个有关边缘求导的示意图:

图片中的大部分边缘都不是突变的而是渐变的,对于斜坡区域,一阶导数将斜坡变成了平坦区域即变成了粗线,二阶导数将斜坡变成了两条中间存在平台区域的细线。
4.3.2边缘提取
在图像上除使用一阶差分来计算相邻像素之间的变化率外,我们还可以利用卷积和特定的算子来计算相邻像素的变化率。prewitt算子和sobel算子可以计算相邻三个点之间的变化率。它们用于一阶算子的边缘检测,利用像素点上下、左右相邻点的灰度差求取边缘。
求梯度有三种卷积核(robert,prewitt,sobel算子),每种卷积核有两个,对图像分别做两次卷积,一个代表水平梯度,一个代表垂直梯度。
1、Prewitt算子
Prewitt的两个算子
计算水平梯度,检测垂直边缘。

计算垂直梯度,检测水平边缘。

2.sobel算子
Sobel算子是典型的基于一阶导数的边缘检测算子,由于该算子中引入了类似局部平均的运算,因此对噪声具有平滑作用,能很好的消除噪声的影响。Sobel算子在Prewitt算子的基础上进行了改进,增强了中间位置的权重。与Prewitt算子、Roberts算子相比效果更好。
计算水平梯度,检测垂直边缘。

计算垂直梯度,检测水平边缘。

Sobel更强调了和边缘相邻的像素点对边缘的影响。相比较Prewitt算子,Sobel算子能够较好的抑制噪声效果。
假设原图像矩阵为A
则有:


4.3.3 sobel算子实例
|
1 2 3 4 5 6 7 8 9 10 11 |
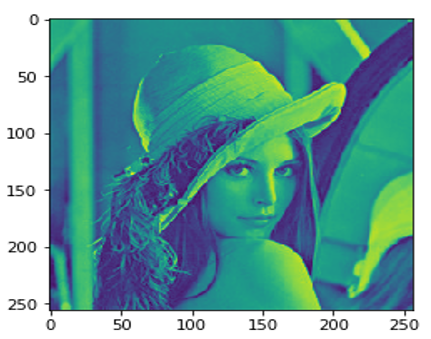
import numpy as np #使用OpenCV开源库读取图片数据 import cv2 from matplotlib import pyplot as plt %matplotlib inline # 把原来彩色图像转换成灰色图像 img = cv2.imread('./data/lena.jpg',cv2.IMREAD_GRAYSCALE) plt.imshow(img) |
运行结果:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def sobel_suanzi(img): r, c = img.shape new_image = np.zeros((r, c)) new_imageX = np.zeros(img.shape) new_imageY = np.zeros(img.shape) s_suanziX = np.array([[-1,0,1],[-2,0,2],[-1,0,1]]) # X方向 s_suanziY = np.array([[-1,-2,-1],[0,0,0],[1,2,1]]) # Y方向 for i in range(r-2): for j in range(c-2): new_imageX[i+1, j+1] = abs(np.sum(img[i:i+3, j:j+3] * s_suanziX)) new_imageY[i+1, j+1] = abs(np.sum(img[i:i+3, j:j+3] * s_suanziY)) new_image[i+1, j+1] = (new_imageX[i+1, j+1]*new_imageX[i+1,j+1] + new_imageY[i+1, j+1]*new_imageY[i+1,j+1])**0.5 #return np.uint8(new_imageX) # return np.uint8(new_imageY) return np.uint8(new_image) # 无方向算子处理的图像 |
执行sobel算子
|
1 2 |
out_sobel = sobel_suanzi(img) plt.imshow(out_sobel) |
运行结果

4.3.4 sobel算子与卷积核
sobel算子与卷积神经网络中的卷积核功能类似。这是卷积核有一个不足:就是提取概要信息,随着层数的增加将不可避免丢失很多信息,为避免这个问题,人们提出残差网络等方法弥补其不足。
【延伸思考】算子不同方向的偏导与卷积核的不同通道的作用有何异同?