Python技术交流与分享

第5章 梯度下降法

机器学习中一项重要任务就是求目标函数（或称为损失函数）的极小值或极大值。通过求目标函数的极值来确定相关权重参数，从而确定模型。如何求目标函数（注，这里的目标函数如果没有特别说明，一般指凸函数）的极值？最常用的一种方法就是梯度下降法。接下来我们将介绍梯度下降法及几种变种方法。

5.1.梯度下降法

梯度不仅是走向极值的方向，而且是下降最快的方向。
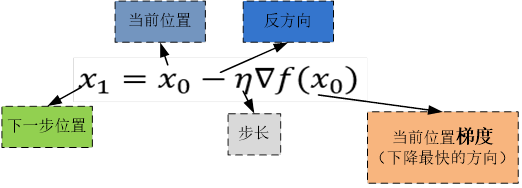
假设函数f(x)的有最小值，如图5-4所示。梯度下降法的数学表达式为：
$x_1=x_0-\lambda\nabla f(x_0)$
其中
1、参数λ称为步长或学习率，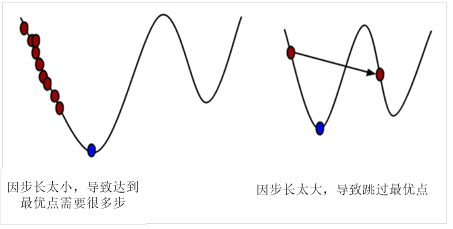
图5-1 学习率对寻找最优点过程的影响
2、这里为何取梯度的负值？
从图5-2可知，无论从左到右还是从右到左，沿梯度的负方向都是指向极小值（如果梯度正方向将指向函数的极大值）。

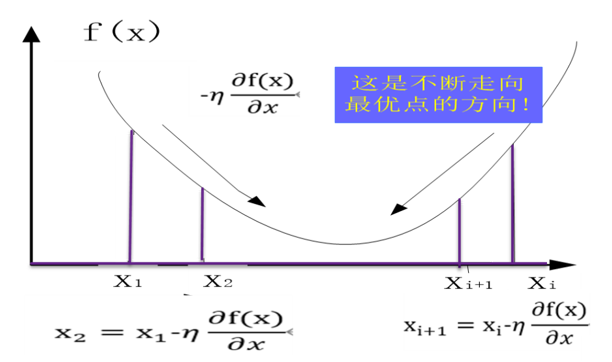
图5-2 梯度下降法示意图
如何理解沿梯度是函数值下降最快的方向呢？下面进行简单说明。
根据导数的定义及泰勒公式，可得函数梯度与函数增量、自变量增量之间的关系。
$f(x+\nabla x)-f(x)=(\nabla f(x))^T \nabla x+o(||\nabla x||)$
如果$\nabla x$足够小，则可以忽略高阶无穷小项，从而得到：
$f(x+\nabla x)-f(x)\approx(\nabla f(x))^T \nabla x$
由于$(\nabla f(x))^T \nabla x=||\nabla f(x)||?||\nabla x||cos\theta$。
其中$\theta$为$\nabla f(x)$与$\nabla x$之间的夹角，由于$-1\leq cos\theta\leq 1$，因此，
如果$\nabla x=-\nabla f(x),cos\theta=-1$，此时，当$||\nabla f(x)||$与$||\nabla x||$一定时，沿梯度的反方向下降最快。
【说明】为何取负梯度？
求极小值，梯度的方向实际就是函数在此点下降最快的方向！而我们需要朝着下降最快的方向走，自然就是负的梯度的方向，所以此处需要加上负号。
如果求极大值，则取梯度的正方向即可。

5.2 单变量函数的梯度下降法

假设函数$f(x)=x^2+3$,
使用梯度下降法，得到极值点。具体采用迭代法，沿梯度方向（或梯度负方向）逐步靠近极值点，如下图所示：

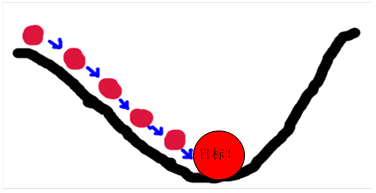
具体实现方法：

用迭代法求函数$f(x)=x^2+3$的最优点。

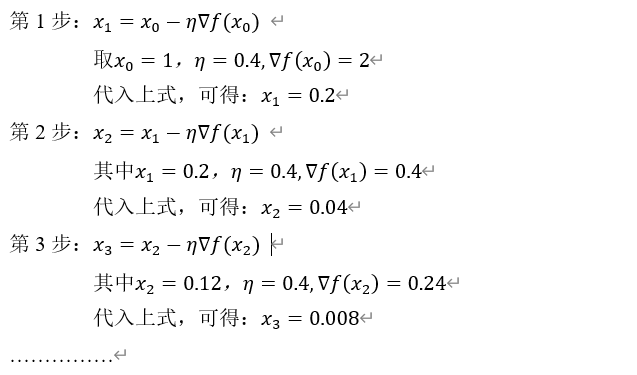
用python代码实现：

运行结果：
x1:0.4000
x2:0.0800
x3:0.0160
x4:0.0032
x5:0.0006
x6:0.0001
x7:0.0000
练习：用梯度下降法求函数$f(x)=(x-1)^2+2$的极值点（迭代3次或以上），并用python实现这个过程。

5.3 多变量函数的梯度下降法

如何用梯度下降方法求极值？以下通过一个简单示例来说明。
假设$f(X)=x_1^2+x_2^2$,该函数的最小值点为(0,0),用梯度下降法来一步步逼近这个最小值点。
假设从点（1,3）开始，学习率设为$\eta=0.1$,函数f(X)的梯度为：
$\nabla f(X)=(2x_1,2x_2)$
梯度方向是下降最快的方向，如下图所示：

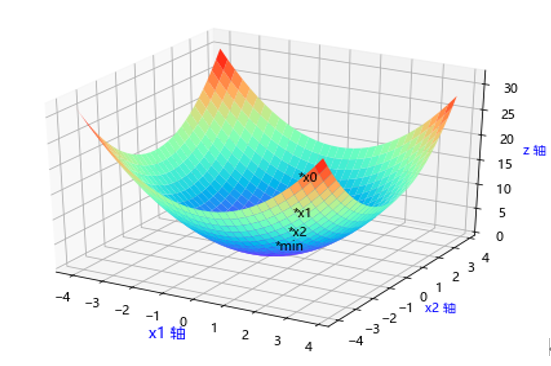
实现上图的python代码：

用Python实现代码以上过程：

运行结果
x1:0.1074,x2:0.3221
x1:0.0115,x2:0.0346
x1:0.0012,x2:0.0037
x1:0.0001,x2:0.0004
x1:0.0000,x2:0.0000
练习：
用梯度下降法求函数$f(x_1,x_2)=(x_1-1)^2+(x_2-1)^2$的最优点，并用python实现并可视化。

5.4 梯度下降法的应用

梯度可以通过迭代的方法来求极值点，但更重要的作用是通过这个过程，来求梯度中的权重参数，从而确定模型。
例如,
求梯度时，往往涉及很多样本，根据这些样本更新参数。每次更新时，如何选择样本是有讲究的。
如果样本总数不大，我们每次更新梯度时，可以使用所有样本。但如果样本比较大，如果每次都用所有样本更新，在性能上不是一个好的方法，这时我们可以采用其它方案，这样既保证效果，又不影响性能。训练时根据样本选择方案不同，大致可分为：
（1）随机梯度下降法
每次求梯度时，不是使用所有样本的数据，而是每次随机选取一个样本来求梯度。这种方法每次更新梯度较快，但这种方法更新梯度振幅较大，如果样本较大，这样方法也非常耗时，效果也不很理想。
（2）批量梯度下降法
针对随机梯度下降法的不足，人们又想到一个两全其美的方法，即批量随机梯度下降法，这种方法每次更新梯度时，随机选择一个批量来更新梯度。这种方法有更好稳定性，同时性能方面也不错，尤其适合与样本比较大时，优势更加明显。
用梯度下降法拟合一条直线：
$h_{\theta} (x)={\theta}_1 x+{\theta}_0$
其中：$\theta_0 ,\theta_1$为参数。
假设y为真实值，根据不同的样本x，代入$h_{\theta}(x)$便可得到预测值。
我们的目标是尽量使真实值y与预测值$h_{\theta}(x)$尽可能接近，换句话，就是使它们之间的距离，通过不断学习样本，不断更新参数$\theta=[\theta_0,{\theta}_1]$，使以下目标函数的值最小。
$L(\theta_0,\theta_1)=\frac{2}{m}\sum_{i=1}^m(y^i-h_{\theta}(x^i))^2$
即：$\underset{\theta_0,\theta_1}{lim}L(\theta_0,\theta_1)$
使用批量梯度下降法处理以上这个回归问题，具体算法如下：
$\theta_i=\theta_i-\lambda\frac{\partial}{\partial\theta_i}L(\theta_0,\theta_1),i=0,1$
写成矩阵的形式：
$h_{\theta}(x)=\theta_0+\theta_1 x_1+\cdots+\theta_n x_n$
用X表示m个样本：$X=\left(\begin{matrix}1&x_1^1&\cdots&x_n^1 \\ \vdots&\vdots&\ddots&\vdots \\ 1&x_1^m&\cdots&x_n^m\end{matrix}\right)$,这是一个$m\times(n+1)$矩阵
$\theta=\left(\begin{matrix}\theta_0 \\ \theta_1\\ \vdots \\ \theta_n\end{matrix}\right)$ 这是一个$(n+1)\times1$矩阵
$X\theta$内积的形状为：$m\times1$
$Y=\left(\begin{matrix}y_1 \\ y_2\\ \vdots \\ y_m\end{matrix}\right)$这是一贯mx1向量，
使用矩阵向量方式定义损失值：

5.5 用Python实现批量梯度下降法

批量梯度下降法用Python实现：

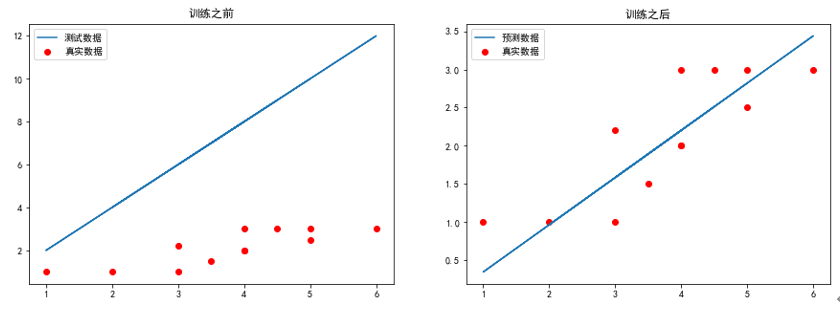
训练模型并可视化运行结果

运行结果如下：
最终j_history值：
[0.10784944]
最终theta值：
[[-0.27223179]
[ 0.6187312 ]]
可视化结果如下：

【说明】

5.6np.array与np.mat的区别

1.生成数组所需数据格式不同
np.mat可以从string或list中生成；而np.array只能从list中生成。
2.生成的数组计算方式不同
np.array生成数组，用np.dot()表示内积，（*）号或np.multiply()表示对应元素相乘。
np.mat生成数组，（*）和np.dot()相同,都表示内积，对应元素相乘只能用np.multiply()。
3.生成维度不同
np.mat只生成2维，np.array可生成n维。
建议使用array格式，因很多numpy函数返回值都是array格式。

5.7 用Python实现随机梯度下降法

1.定义损失函数、梯度函数

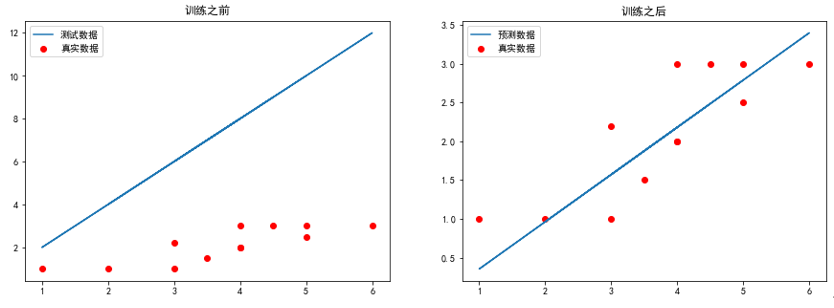
2.运行梯度函数及可视化运行结果

3.运行结果
最终j_history值：
[0.07909981]
最终theta值：
[-0.25281579 0.60842649]

【练习】
把数据集改为：
m = 100000
x1 = np.random.normal(size = m)
X = x1.reshape(-1,1)
y = 4. * x1 + 3. +np.random.normal(0,3,size = m)
x= np.hstack([np.ones((len(x1),1)), X])