第2章 随机事件与概率
2.1 随机事件
随机事件是在随机试验中,可能出现也可能不出现,而在大量重复试验中具有某种规律性的事件叫作随机事件(简称事件)。
随机事件通常用大写英文字母A、B、C等表示。随机试验中的每一个可能出现的试验结果称为这个试验的一个样本点,记作 。全体样本点组成的集合称为这个试验的样本空间,记作
。全体样本点组成的集合称为这个试验的样本空间,记作 .即
.即 。仅含一个样本点的随机事件称为基本事件,某些样本点组成的集合称为随机事件(random event),简称为事件。
。仅含一个样本点的随机事件称为基本事件,某些样本点组成的集合称为随机事件(random event),简称为事件。
整个样本空间 也是个事件,它一定会发生,称为必然事件。空集
也是个事件,它一定会发生,称为必然事件。空集 也是个事件,它不可能发生,称为不可能事件。
也是个事件,它不可能发生,称为不可能事件。
例如,投骰子,记整数i表示“投掷结果为i”这个样本点,那么样本空间 ={1,2,3,4,5,6},事件A={1,3,5} 表示“投掷的结果为奇数”
={1,2,3,4,5,6},事件A={1,3,5} 表示“投掷的结果为奇数”
2.2 事件与集合
随机事件是用集合定义的,这里我们不区分事件和集合,对事件可以做集合的各种运算。
事件A和B的交集,表示事件A和B同时发生,由事件A与事件B的公共样本点组成记,记为 或AB,如图2-2(a)所示。
或AB,如图2-2(a)所示。
事件A和B的并集,由事件A与事件B所有样本点组成,记为 或A+B,如图2-2(b)所示。
或A+B,如图2-2(b)所示。
差事件,即事件A发生且事件B不发生,是由属于事件A但不属于事件B的样本点组成,记作A-B,如图2-2(c)所示。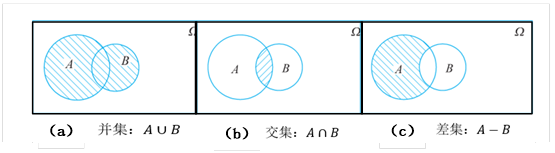
图2-2 随机事件之间的关系
互斥事件(互不相容事件)事件A与事件B,事件A与事件B不能同时发生,事件A与事件B没有公共的样本点,记为 。
。
事件A的对立事件,事件A不发生,事件A的对立事件是由不属于事件A的样本点组成,记作 。
。
事件满足如下运算:
在随机事件中,有许多事件,而这些事件之中又有联系,分析事件之间的关系,可以帮助我们更加深刻地认识随机事件;给出的事件的运算及运算规律,有助于我们分析更复杂事件。
(1)交换律

(2)结合律

(3)分配律
 如图2-3(a)
如图2-3(a)
 如图2-3(b)
如图2-3(b)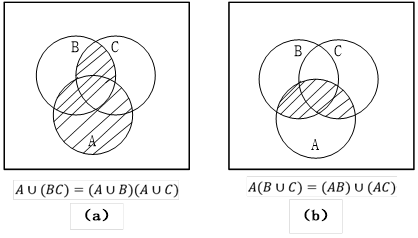
图2-3 随机事件的分配律
(4)摩根律


可推广到n个事件。
2.3 随机事件的概率
既然事件可用集合来表示,那么事件的关系和运算自然应当按照集合论中集合之间的关系和集合的运算来处理。接下来给出这些关系和运算在概率论中的提法,并根据“事件发生”的含义,用概率来度量随机事件发生的可能性。
随机事件A的概率记为p(A),表示此事件发生的可能性,其值满足:

概率值越大则事件越可能发生。概率为0意味着这个事件不可能发生(不可能事件),概率为1意味着这个事件必然发生(必然事件)。
一般情况下,假设样本空间Ω为有限集,其中每个样本点发生的概率是相等的(这也是古典概型的重要假设),因此事件A发生的概率是该集合的基本事件数(或简称为基数)与整个样本空间基数的比值:

例2:在掷骰子试验中,看朝上面的点数,则有样本空间为 ={1, 2, 3, 4, 5, 6}
={1, 2, 3, 4, 5, 6}
求事件A={点数为奇数},B={点数为小于4的奇数},事件C={点数为偶数}的概率、
解:事件A包括的基本样本点为{1,3,5},B事件包括的基本样本点为{1,3},C事件包括的基本样本点为{2,4,6}
所以|A|=3,|B|=2, |C|=3而
从而的:
事件A的概率
事件B的概率
事件C的概率
对应集合的交运算就是两个事件同时发生的概率,记为 或p(A,B),其概率为:
或p(A,B),其概率为:

对应集合的并运算就是两个事件至少有一个发生的概率,其概率为:

因为
所以
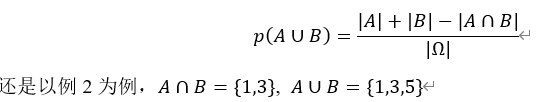
所以
前面介绍的概率均针对有限或无限可数的样本空间,与之相对的还有无限不可数样本空间,这类概率称为几何型概率。几何型概率定义在无限不可数数据集上,根据测度值(如长度、面积、体积等)的定义。事件A发生的概率为A所在区域的测度值与样本空间 测度值的比值,即
测度值的比值,即
几何概型与古典概型类似,也要求样本空间有一种均匀性。
例3:在区间[-1,1]上随机取一个数x,求使 的值基于0和
的值基于0和 之间A事件的概率。
之间A事件的概率。
解:由图2-4可知,
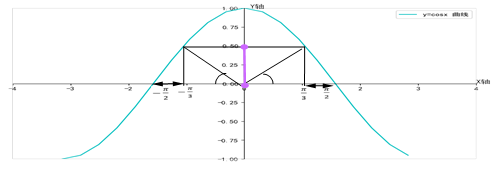
图2-4 y=cosx函数曲线
满足条件的x需在以下范围即可:
2.4 条件概率
生活中很多事件是有因果关系或前后关系,这节介绍的条件概率就是研究随机事件间的前后依赖关系。条件概率是指事件A在另外一个事件B已经发生条件下发生概率。条件概率表示为:P(A|B),读作“在B发生的条件下A发生的概率”。如果P(B)>0,条件概率可按下列公式计算:

在古典概型中,在已知B发生时,认为B集合中的那些样本点数为|B| ,而其中同时也在A集合中的样本点有 个,故
个,故
在几何概型中,条件概率的解释则更为直观,如图2-5所示
题图2-5 条件概率模型
已知B发生时,样本空间中只剩下了B中的那些样本点(图中有色区域),此时A发生的概率就是(A,B)的面积(阴影部分)比上B的面积,即

例3:投掷一次骰子,该骰子一共有6个面,分别为1,2,3,4,5,6。
问:已知向上的点数是偶数,那么该点数大于4的概率是多少?
解:这是一个条件概率问题,设B={向上的点数为偶数}={2,4,6}、A={点数大于4}={5,6}
根据式(2.2)可得:
2.5 事件的独立性
事件的独立性指的就是互不影响事件,或一个事件的发生不影响另一个事件的发生。利用独立性可以简化概率的计算。
如果p(A|B)=p(A),或p(B|A)=p(B),则称随机事件A和B独立。
如果随机事件A和B独立,根据式(2.3)可得:
p(A,B)=p(A)P(B) (2.5)
对式(2.5)推广到n个随机事件,如果 互相独立,则对所有可能组合
互相独立,则对所有可能组合
 ,都有
,都有




【说明】
(1)互相独立非两两独立,相互独立的条件强于两两独立。
(2)两个随机事件独立与两个随机事件不相容的区别,后者是两个事件不可能同时发生,即p(A,B)=0。
2.6 全概率公式
式(2.6)称为全概率公式,图2-6能更直观说明全概率公式的含义。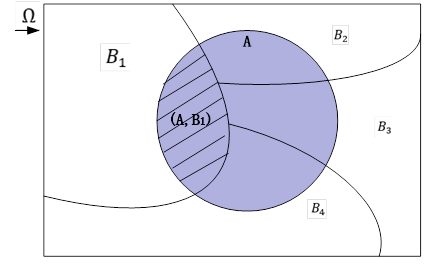
图2-6 全概率模型示意图
因 是图2-6阴影部分的概率,对所有的i求和,就得到A的概率。全概率公式的应用之一,如果事件A的概率很难算,可以试着构造完备事件组,如果每个
是图2-6阴影部分的概率,对所有的i求和,就得到A的概率。全概率公式的应用之一,如果事件A的概率很难算,可以试着构造完备事件组,如果每个 的概率容易算,并且在
的概率容易算,并且在 发生的条件下
发生的条件下 也容易算,那么就可以通过全概率公式计算出A的概率。
也容易算,那么就可以通过全概率公式计算出A的概率。
例5:假设有10人抽签,其中有且仅有1个人会中签,每个人依次抽签,则事件A={第2个人中签}的概率是多少?
解:直接求第2人中签的概率不是很好求,此时可以使用全概率公式来简化这个问题,很明显,第2人是否中签,与第1人是否中签有一定关系。考虑第1人的中签情况,问题就简单了,思路也更清晰了。
设B={第1个人中签},则 ={第1人没中签},事件B和
={第1人没中签},事件B和 构成一个完备事件组。根据全概率公式可得:
构成一个完备事件组。根据全概率公式可得:


代入上式可得:

用类似的方法可推出:所有人的中签概率都是 ,所以从数学上来说,抽签顺序并不会影响中签概率,大家机会均等。
,所以从数学上来说,抽签顺序并不会影响中签概率,大家机会均等。
2.7 贝叶斯定理
贝叶斯定理是概率论中的一个定理,它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解释中,贝叶斯定理(贝叶斯公式)能够告知我们如何利用新证据修改已有的看法。这个名称来自于托马斯·贝叶斯。
通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的;然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式的一个用途在于通过已知的三个概率函数推出第四个。
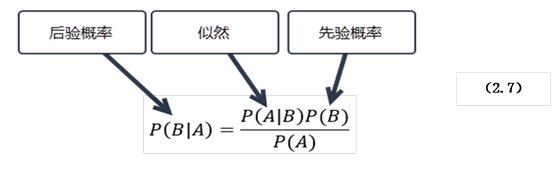
贝叶斯公式为:
在贝叶斯定理中,每项都有约定俗成的名称:
P(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
P(B)是B的先验概率(或边缘概率)。之所以称为"先验"是因为它不考虑任何A方面的因素。
P(A|B)是已知B发生后A的条件概率,也称为似然(likelihood)函数,也由于得自B的取值而被称作A的后验概率。
P(A)是A的先验概率或边缘概率。
其中P(A)的计算,通常使用全概率公式,设 (其中
(其中 两两互斥),则
两两互斥),则

从而有:

对任意B_j,贝叶斯公式又可表示为:

例6:利用贝叶斯定理进行分类--简单实例
假设某医院早上收了六个门诊病人,如下表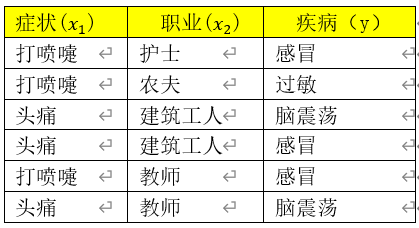
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上脑震荡的概率有多大?
4、简单入手
根据式(贝叶斯公式)可得:
P(感冒|(打喷嚏,建筑工人))
= P((打喷嚏,建筑工人)|感冒) x P(感冒)
/ P(打喷嚏,建筑工人)
假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了:
P(感冒|(打喷嚏,建筑工人))
= P((打喷嚏|感冒)xP(建筑工人)|感冒) x P(感冒)
/ P(打喷嚏) xP(建筑工人)
由此可得:
P(感冒|(打喷嚏,建筑工人))
= 
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
5、Python实现
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
# -*- coding: utf-8-*- from pandas import DataFrame import numpy as np import pandas as pd #inputfile = r'C:\Users\lenovo\bys_class1.csv' #data = pd.read_csv(inputfile,header=0,encoding='utf-8') #生成数据 data = [ {"f1":"打喷嚏", "f2":"护士", "c1":"感冒"}, {"f1":"打喷嚏", "f2":"农夫", "c1":"过敏"}, {"f1":"头痛", "f2":"建筑工人", "c1":"脑震荡"}, {"f1":"头痛", "f2":"建筑工人", "c1":"感冒"}, {"f1":"打喷嚏", "f2":"教师", "c1":"感冒"}, {"f1":"头痛", "f2":"教师", "c1":"脑震荡"}] #第七个病人,是一个打喷嚏的建筑工人。他患上感冒、过敏或脑震荡的概率 def P1(c_type): #c_type 为感冒或过敏或脑震荡 df=DataFrame(data) count=df.shape[0] gm=df.loc[df['c1'].isin([c_type])].shape[0] dpt=df.loc[df['f1'].isin(["打喷嚏"])].shape[0] jzgr=df.loc[df['f2'].isin(["建筑工人"])].shape[0] dpt_gm=df.loc[df['c1'].isin([c_type])].loc[df['f1'].isin(["打喷嚏"])].shape[0] jzgr_gm=df.loc[df['c1'].isin([c_type])].loc[df['f2'].isin(["建筑工人"])].shape[0] p_gm=gm/count p_dpt=dpt/count p_jzgr=jzgr/count #计算条件概率 p_dpt_gm=dpt_gm/gm p_jzgr_gm=jzgr_gm/gm p=(p_dpt_gm*p_jzgr_gm*p_gm)/(p_dpt*p_jzgr) return p print("第7个人患感冒的概率%.3f"%P1("感冒")) print("第7个人患过敏的概率%.3f"%P1("过敏")) print("第7个人患脑震荡的概率%.3f"%P1("脑震荡")) |
打印结果
第7个人患感冒的概率0.667
第7个人患过敏的概率0.000
第7个人患脑震荡的概率0.000
2.8 条件独立
前面我们介绍了条件概率和事件的独立性,两者结合可以给出条件独立的概念。给定三个随机事件A,B,C,如果满足:
p(A|B,C)=p(A|C)
则称A和B关于C条件独立。与之等价的一个判断条件是:
p(A,B|C)=p(A|C)p(B|C)
该定义可以推广到n个事件的情况:

A和B关于C条件独立,可记为: 这里垂直符表示独立。条件独立的概念在朴素贝叶斯分类器、概率图模型中经常使用。
这里垂直符表示独立。条件独立的概念在朴素贝叶斯分类器、概率图模型中经常使用。