第3章 随机变量及其分布
3.1 从随机事件到随机变量
随机试验中，每一个可能的结果，在试验中发生与否，都带有随机性，所以称为随机事件。而所有可能结果构成的全体，称为样本空间。为了更好分析处理这些随机事件，人们就想到了把随机事件数量化，数量化的载体就是随机变量，随机变量一般用大写字母表示，如X,Y,Z,W等，随机变量的取值一般用小写字母表示，如x,y,x_i等，图3-1说明随机事件与随机变量的对应关系示意图。
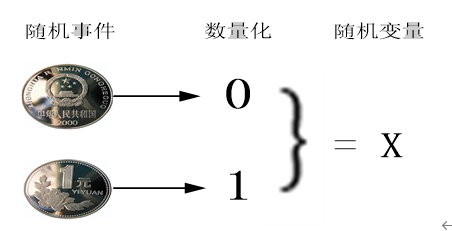
图3-1 随机事件
数量化随机变量过程示意图
随机变量（random variable）表示随机试验各种结果的实值单值函数。随机事件不论与数量是否直接有关，都可以数量化，即都能用数量化的方式表达。 例如投掷硬币的正反面，掷骰子的点数，某一时间内公共汽车站等车乘客人数，灯泡的寿命等等，都可用随机变量表示。
例1：将一枚硬币抛掷三次，观察出现正面和方面的情况，样本空间是
={正正正,正正反,正反正,反正正,正反反,反正反,反反正,反反反}
以X记三次投掷得到正面的总数，那么，对于样本空间Ω中的每一个样本点
，如式（3.1）所示，X都有一个数与之对应，X就是把随机事件数量化的随机变量，X与随机事件的关系为：
随机变量的取值随试验的结果而定，而试验的各个结果出现有一定概率，因而随机变量的取值有一定概率，例如，本例中的X取值为2，记成X=2,对应样本点的集合A={正正反,正反正,反正正},这是一个事件，当且仅当A发生时有X=2。我们称概率p(A)=p{正正反,正反正,反正正}为X=2的概率，记为
。类似地有
对于一个随机变量，不仅要说明它能够取什么值，更需要关心取这些值的概率(分布函数)，这也是随机变量与一般变量的本质区别。
引入随机变量，就可利用数学分析的方法对随机试验的结果进行分析研究了。