3.7随机变量函数的分布

3.7.1 随机变量函数的分布

随机变量函数是以随机变量为自变量的函数，它将一个随机变量映射成另一个随机变量，二者一般有不同的分布。
定理：设随机变量X具有概率密度f_X(x),-\infty<x<\infty,关于X的函数 Y=g(X) 且函数g(x)处处可导，g'(x)>0或g'(x)<0 ,反函数存在，g(x)的反函数g^{-1}(x)=h(x)，则Y是连续型随机变量，其概率密度为
f_Y(y)=f(x)=\begin{cases}f_X(x)(h(y))|h'(y)|,&\alpha<y<\beta\\0,&other\end{cases}
其中 \alpha=min\{g(-\infty),g(\infty)\},\beta=max\{g(-\infty),g(\infty)\} 证明：先证g'(x)>0 (即函数g(x)为单调递增的情况)
设随机变量X,Y的分布函数分别为F_X(x),F_Y(y),先求随机变量Y的分布函数F_Y(y)。
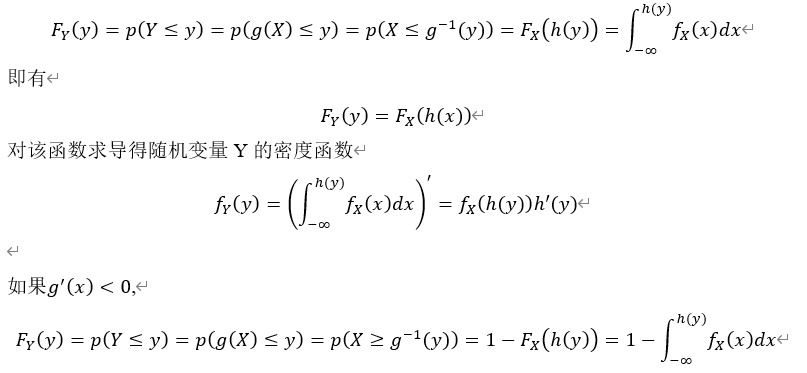
对该函数求导得随机变量Y的密度函数
这个结论可以推广到n个互相独立的随机变量的情况。

3.7.2 多维随机变量函数的分布

其中|J|为雅可比行列式的绝对值。

3.7.3 高斯混合模型

高斯混合模型（Gaussian Mixed Model，缩写为GMM）指的是多个高斯分布函数的线性组合，其概率密度函数定义为
p(x)=\sum_{i=1}^K\omega_i N(x|\mu_i,\Sigma_i)
其中x为随机向量，K为高斯分布的数量，\omega_i为选择第i个高斯分布的概率（或权重），\mu_i,\Sigma_i分别为第i个高斯分布的均值向量、方差矩阵。选择第i个高斯分布的\omega_i满足概率的规范：
\omega_i\ge 0,\Sigma_{i=1}^K\omega_i =1
理论上GMM可以拟合出任意类型的分布，图3-7为一维高斯混合模型的概率密度函数图像，该概率密度函数为3个高斯分布线性组合，具体表达式为
p(x)=0.2*N(X|1.0,{0.5}^2 )+0.3*N(X|2.0,{1.0}^2 )+0.5*N(X|3.0,{1.5}^2 )

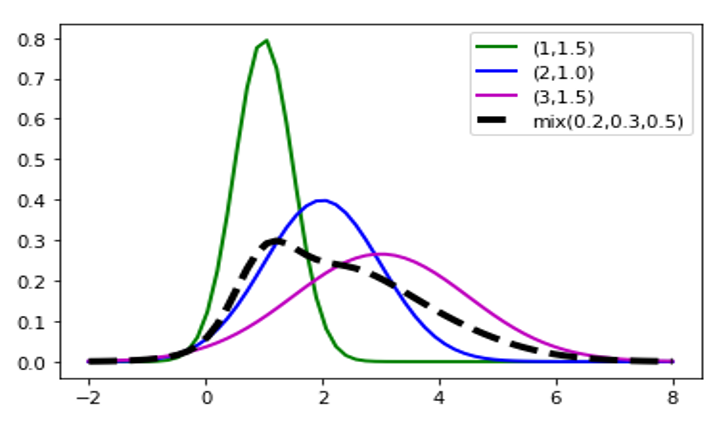
图3-7 一维高斯混合模型的概率密度函数图像
通常用于解决同一集合下的数据包含多个不同的分布的情况（或者是同一类分布但参数不一样，或者是不同类型的分布等情况）。如图3-8所示，由2个高斯分布得到二维高斯混合模型生成的2类样本。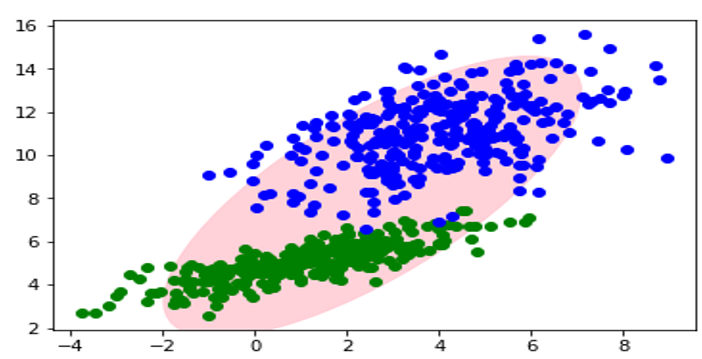
图3-8二维高斯混合模型生成的样本
从图3-8可知，很多数据集可以看成是GMM生成的样本数据，为此，我们可以反过来，根据已知样本数据，推导出产生样本数据背后的GMM。这方面的应用非常广泛，如基于GMM的聚类算法就是典型案例之一。
K均值算法（k-means）是聚类算法的代表，其主要思路是：
（1）选择k个类族中心；
（2计算各点到各族中心距离，将样本点划分到最近的类簇中心；
（3）重新计算k个类族中心；
（4）不断迭代直至收敛。
不难发现这个过程和EM迭代的方法极其相似，事实上，若将样本的类族数看做为“隐变量”Z，类族中心看作样本的分布参数θ，k-means就是通过EM算法来进行迭代的，
与我们这里不同的是，k-means的目标是最小化样本点到其对应类中心的距离和，基于GMM的聚类方法将采用极大化似然函数的方法估计模型参数。
如何计算高斯混合模型的参数呢？这里我们像单个高斯模型那样使用最大似然法来，因为对于每个观测数据点来说，事先并不知道它是属于哪个子分布的（属于哪个分布属于隐变量），因此似然函数中的对数里面还有求和，对于每个子模型都有未知的参数\omega_i,\mu_i,\Sigma_i，这就是GMM参数估计的问题。要解决这个问题，直接求导无法计算,可以通过迭代的EM算法求解。具体的EM算法，参数估计部分将详细介绍。