5.2 极大后验概率估计

极大似然估计将参数θ看作是确定值，但其值未知，即是一个普通变量，是属于频率派，与频率派相对应的就是贝叶斯派，极大后验概率、EM算法等属于贝叶斯派。

5.2.1频率派与贝叶斯派的区别

关于参数估计，统计学界的两个学派分别提供了两种不同的解决方案。
频率派认为参数虽然未知，但是客观存在的固定值，通过优化似然函数等准则来确定其值。
贝叶斯派认为参数是未观察到的随机变量，其本身也可有分布，因此，可假定参数服从一个先验分布，然后基于观测到的数据来计算参数的后验分布，比如极大后验概率。

5.2.2经验风险最小化与结构风险最小化

经验风险最小化与结构风险最小化是对于损失函数而言的。可以说经验风险最小化只侧重训练数据集上的损失降到最低；而结构风险最小化是在经验风险最小化的基础上约束模型的复杂度，使其在训练数据集的损失降到最低的同时，模型不至于过于复杂，相当于在损失函数上增加了正则项，防止模型出现过拟合状态。这一点也符合奥卡姆剃刀原则-简单就是美。
经验风险最小化可以看作是采用了极大似然的参数评估方法，更侧重从数据中学习模型的潜在参数，而且是只看重数据样本本身。这样在数据样本缺失的情况下，模型容易发生过拟合的状态。
而结构风险最小化为了防止过拟合而提出来的策略。过拟合问题往往是由于训练数据少和噪声以及模型能力强等原因造成的。为了解决过拟合问题，一般在经验风险最小化的基础上再引入参数的正则化，来限制模型能力，使其不要过度地最小化经验风险。
在参数估计中，结构风险最小化采用了最大后验概率估计的思想来推测模型参数，不仅仅是依赖数据，还依靠模型参数的先验分布。这样在数据样本不是很充分的情况下，我们可以通过模型参数的先验分布，辅助以数据样本，做到尽可能的还原真实模型分布。
根据大数定律，当样本容量较大时，先验分布退化为均匀分布，称为无信息先验，最大后验估计退化为最大似然估计。

5.2.3 极大大后验概率估计

极大后验概率估计将参数θ视为随机变量，并假设它服从某种概率分布。通过最大化后验概率p(\theta|x)来确定其值。即在样本出现的情况条件下，最大化参数的后验概率。求解时需要假设参数\theta服从某种分布，这个分布需要预先知道，故又称为先验概率。
假设参数\theta服从分布的概率函数为p(\theta|x)根据贝叶斯公式，参数\theta对已知样本的后验概率为：
p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)} \tag{5.4}
考虑到其中概率p(x)与参数\theta无关，所以，最大化后验概率p(\theta|x)等价于最大化p(x|\theta)p(\theta)，即：
\underset{\theta}{argmax} p(\theta|x)= \underset{\theta}{argmax} p(x|\theta)p(\theta)\tag{5.5}
由此可得极大后验概率的对数似然估计为：
\hat{\theta}=\underset{\theta}{argmax}log L(\theta)=\underset{\theta}{argmax}(\sum_{i=1}^n logp(x_i|\theta)+logp(\theta) )\tag{5.6}
式（5.5）比式（5.2）多了logp(\theta)这项，如果参数\theta服从均匀分布，即其概率函数为一个常数，则最大化后验概率估计与最大化参数估计一致。或者，也可以反过来，认为MLE是把先验概率p(\theta)认为等于1，即认为\theta是均匀分布。
例1：假设n个样本，它们属于伯努利分布B(p),其中取值为1的样本有m个，取值为0的样本有n-m个，假设参数p服从正态分布N(0.3,0.01),样本集的极大后验概率函数为：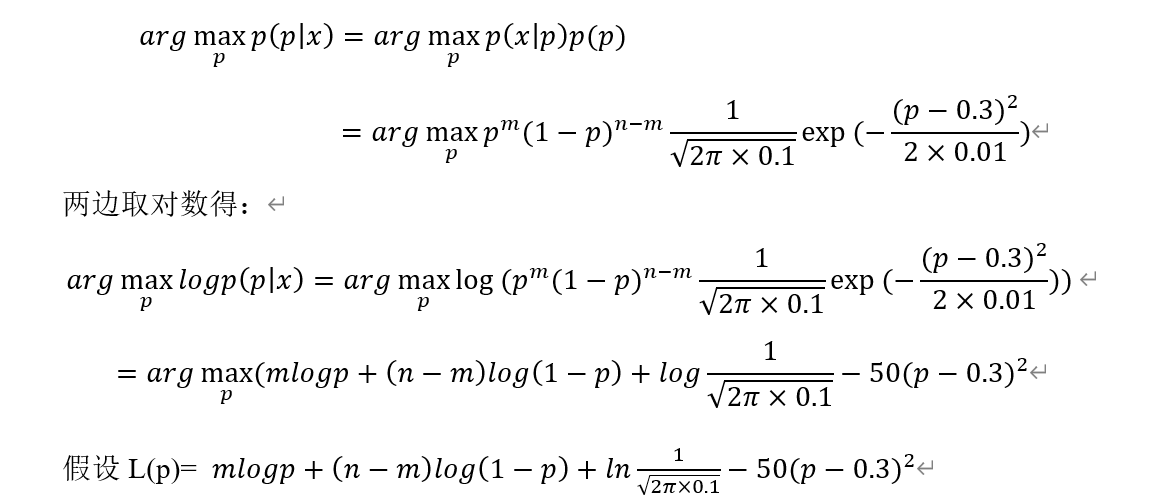
为求L(p)的最大值，对其求导，并令导数为0，可得：
\frac{m}{p}-\frac{n-m}{1-p}-100(p-0.3)=0
其中0<p<1,当n=100，m=30时，可解得：
p=0.3
这个值与极大似然估计的计算的值一样。

5.2.4 极大后验概率估计的应用

极大后验概率估计与极大似然估计相比，多了一个先验概率p(\theta),通过这个先验概率可以给模型增加一些正则约束。假设模型的参数\theta服从正太分布。
p(\theta)=\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(\theta-\mu)^2}{2\sigma^2})
其中正态分布的参数\mu,\sigma为已知。由式（5.6）可知，随机变量\theta的极大后验概率估计为
\hat{\theta}=\underset{\theta}{argmax}(\sum_{i=1}^n logp(x_i|\theta)+logp(\theta) )
其中
在极大似然估计的基础上加了正态分布的先验，这等同于在已有的损失函数上加了L2正则。
可以看出，最大后验概率等价于平方损失的结构风险最小化。