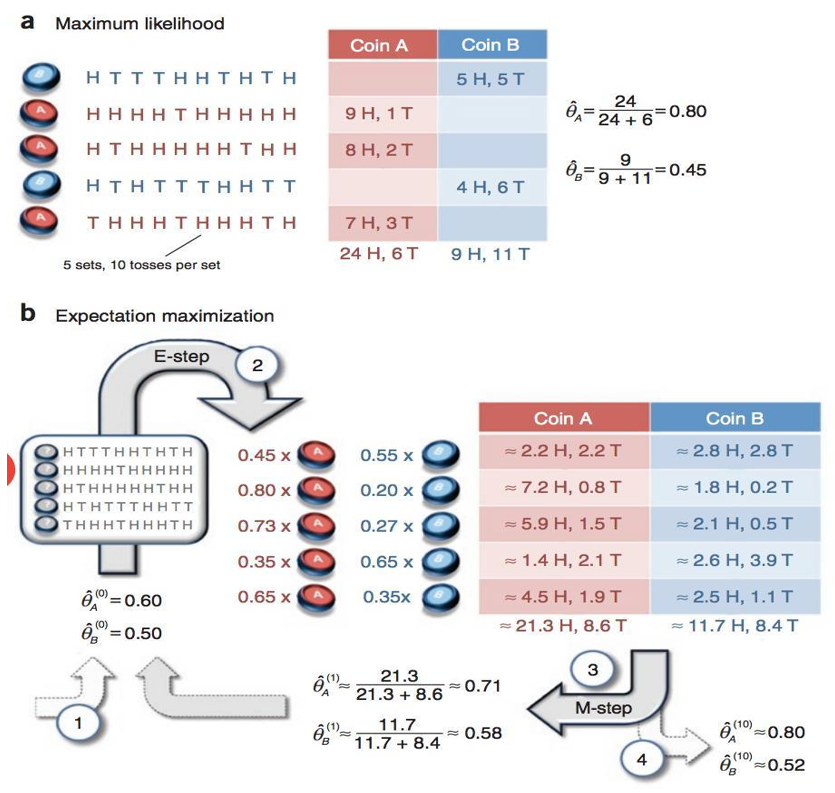
5.3.3 EM算法简单实例
根据表2的情况可知,只要知道Z,就能求出参数 。但要知道Z,又必须通过参数
。但要知道Z,又必须通过参数 推导出来,否则无法推出z的具体情况。为此,我们可以把Z看成一个隐变量,这样完整的数据就是(X,Z),通过极大似然估计对参数
推导出来,否则无法推出z的具体情况。为此,我们可以把Z看成一个隐变量,这样完整的数据就是(X,Z),通过极大似然估计对参数 进行估计,因存在隐变量z,一般无法直接用解析式表达参数,故采用迭代的方法进行优化,具体步骤如下:
进行估计,因存在隐变量z,一般无法直接用解析式表达参数,故采用迭代的方法进行优化,具体步骤如下:
输出:模型参数
EM算法具体步骤
(1)先初始化参数
(2)假设第t次循环时参数为 ,求Q函数
,求Q函数

(3)对Q函数中的参数 实现极大似然估计,得到
实现极大似然估计,得到

(4)重复第(2)和(3)步,直到收敛或指定循环步数。
其中第(2)步需要求 ,我们定义为:
,我们定义为: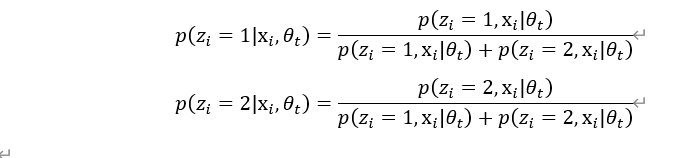
根据这个迭代步骤,第1次迭代过程如下:
(1)初始化参数
(2)E步,计算Q函数
先计算隐含变量的后验概率:

按同样方法,完成剩下4轮投掷,最后得到投掷统计信息如下表所示: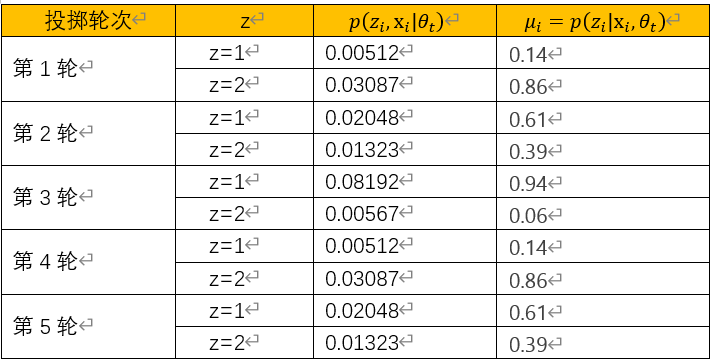
 的实现过程可用二项分布的实现,具体过程如下:
的实现过程可用二项分布的实现,具体过程如下:
计算Q函数,设 表示第i轮投掷出现正面的次数。
表示第i轮投掷出现正面的次数。
(3)对Q函数中的参数 实现极大似然估计,得到
实现极大似然估计,得到

对Q函数求导,并令导数为0。
所以
进行第2轮迭代:
基于第1轮获取的参数 ,进行第2轮EM计算:
,进行第2轮EM计算:
计算每个实验中选择的硬币是1和2的概率,计算Q函数(E步),然后在计算M步,得
继续迭代,直到收敛到指定阈值或循环次数。
以上计算过程可用Python实现
具体代入如下:
把硬币1用A表示,硬币1用B表示。H(或1)表示正面朝上,T(或0)表示反面朝上。
1、导入需要的库
|
1 2 |
import numpy as np from scipy import stats |
2、把观察数据写成矩阵
|
1 2 3 4 5 6 |
# 硬币投掷结果观测序列 observations = np.array([[1, 1, 0, 1, 0], [0, 0, 1, 1, 0], [1, 0, 0, 0, 0], [1, 0, 0, 1, 1], [0, 1, 1, 0, 0]]) |
3、单步EM算法,迭代一次算法实现步骤
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
def EM_Single(priors, observations): """ EM算法单次迭代 参数初始化 : [theta_A, theta_B] 输入样本矩阵: [m x n matrix] 返回值 -------- 新参数值: [new_theta_A, new_theta_B] """ counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}} theta_A = priors[0] theta_B = priors[1] u_A=[] u_B=[] # E step for observation in observations: len_observation = len(observation) num_heads = observation.sum() num_tails = len_observation - num_heads # 投掷硬币A(或B)五次,这是一个二项分布问题 contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A) contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B) #求权重时,把二项分布中的组合数约去了 weight_A = contribution_A / (contribution_A + contribution_B) #取2位小数 weight_A=round(weight_A,2) weight_B = contribution_B / (contribution_A + contribution_B) #取2位小数 weight_B=round(weight_B,2) # 更新在当前参数下A、B硬币产生的正反面次数 counts['A']['H'] += weight_A * num_heads u_A.append(weight_A) counts['B']['H'] += weight_B * num_heads u_B.append(weight_B) # M step new_theta_A = counts['A']['H'] / (len_observation*np.sum(u_A)) new_theta_B = counts['B']['H'] / (len_observation*np.sum(u_B)) new_theta_A=round(new_theta_A,2) new_theta_B=round(new_theta_B,2) return [new_theta_A, new_theta_B] |
4、执行
|
1 |
EM_Single([0.2,0.7],observations) |
[0.35, 0.53]
与手工计算的结果一致。
5、EM算法主循环
EM算法的主循环,给定循环的两个终止条件:模型参数变化小于阈值;循环达到最大次数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
def EM(observations, prior, tol=1e-6, iterations=10): """ EM算法 :param observations: 观测数据 :param prior: 模型初值 :param tol: 迭代结束阈值 :param iterations: 最大迭代次数 :return: 局部最优的模型参数 """ iteration = 0 while iteration < iterations: new_prior = EM_Single(prior, observations) delta_change = np.abs(prior[0] - new_prior[0]) if delta_change < tol: break else: prior = new_prior iteration += 1 return [new_prior, iteration] |
6、测试
|
1 |
EM(observations, [0.20, 0.70],iterations=1) |
运行结果
[[0.35, 0.53], 1]
|
1 |
EM(observations, [0.20, 0.70],iterations=2) |
运行结果
[0.4, 0.48], 2]
|
1 |
EM(observations, [0.20, 0.70],iterations=10) |
运行结果
[[0.44, 0.44], 5]
练习
用python实现以下这个简单实例: