5.3.5 EM算法的收敛性
要证明通过迭代法求得的参数 收敛于极值点,如果能证明对应的似然函数
收敛于极值点,如果能证明对应的似然函数 收敛即可。要证明似然函数收敛,因似然函数
收敛即可。要证明似然函数收敛,因似然函数 有上界,如果能证明通过迭代,似然函数递增,则
有上界,如果能证明通过迭代,似然函数递增,则 收敛于极值点。
收敛于极值点。
假设第t次迭代时的参数为 ,通过t+1次迭代后参数为
,通过t+1次迭代后参数为 ,接下来证明
,接下来证明 。
。
由式(5.13)可得: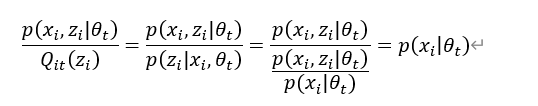
运算结果与隐变量 无关,是一个常数,根据Jensen不等式可知,式(5.12)中作为第t次迭代的结果,即把
无关,是一个常数,根据Jensen不等式可知,式(5.12)中作为第t次迭代的结果,即把 视为
视为 ,
, 改为
改为 ,则其中不等式可以取等号,即有:
,则其中不等式可以取等号,即有: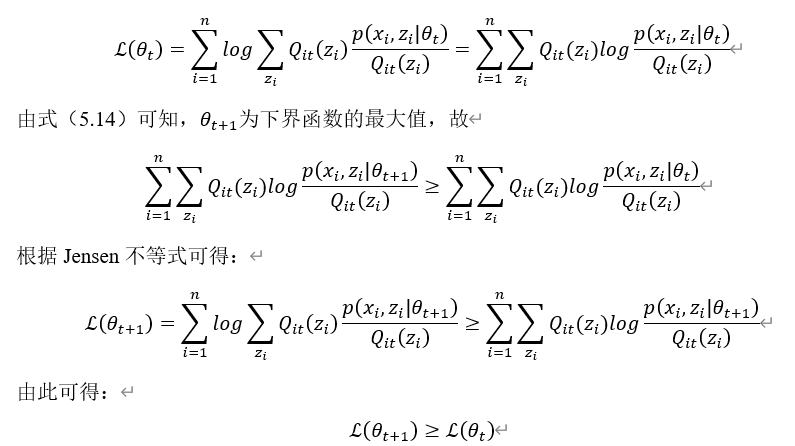
似然函数与其下界函数之间的关系,可以通过图5-10直观表示。
图5-10 EM算法中目标函数与下界函数的之间的关系