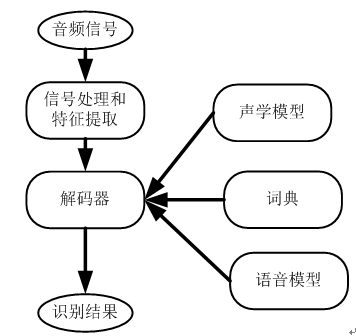
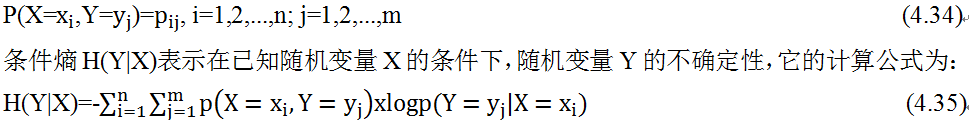本章利用Scrapy架构,实现一个爬虫任务,从一个网站爬取一些教师信息(如教师姓名、职称、简介),然后把爬取的信息分别存放到cvs文件、MySQL。
环境为python3.6
4.1 Scrapy 框架入门简介
4.1.1 Scrapy 框架
Scrapy是用纯Python实现一个为了爬取网站数据、提取结构性数据而编写的应用框架,用途非常广泛。框架的力量,用户只需要定制开发几个模块就可以轻松的实现一个爬虫,用来抓取网页内容以及各种图片,非常之方便。Scrapy 使用了 Twisted'twɪstɪd异步网络框架来处理网络通讯,可以加快我们的下载速度,不用自己去实现异步框架,并且包含了各种中间件接口,可以灵活的完成各种需求。
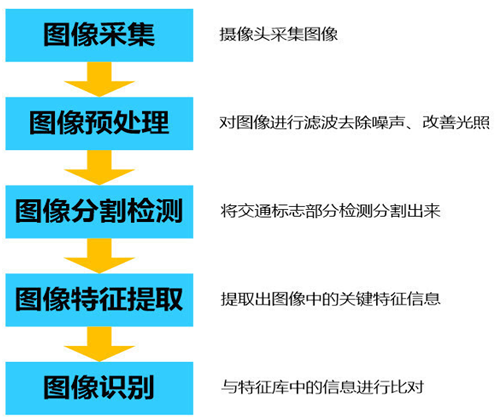
Scrapy架构图(其中绿线是数据流向)

Scrapy Engine(引擎):
负责Spider、ItemPipeline、Downloader、Scheduler中间的通讯,信号、数据传递等。
Scheduler(调度器):
它负责接受引擎发送过来的Request请求,并按照一定的方式进行整理排列,入队,当引擎需要时,交还给引擎。
Downloader(下载器):
负责下载Scrapy Engine(引擎)发送的所有Requests请求,并将其获取到的Responses交还给Scrapy Engine(引擎),由引擎交给Spider来处理,
Spider(爬虫):
它负责处理所有Responses,从中分析提取数据,获取Item字段需要的数据,并将需要跟进的URL提交给引擎,再次进入Scheduler(调度器),
Item Pipeline(管道):
它负责处理Spider中获取到的Item,并进行进行后期处理(详细分析、过滤、存储等)的地方.
Downloader Middlewares(下载中间件):
你可以当作是一个可以自定义扩展下载功能的组件。
Spider Middlewares(Spider中间件):
你可以理解为是一个可以自定扩展和操作引擎和Spider中间通信的功能组件(比如进入Spider的Responses;和从Spider出去的Requests)
4.1.2 Scrapy 流程
Scrapy运行流程大概如下:
引擎从调度器中取出一个链接(URL)用于接下来的抓取
引擎把URL封装成一个请求(Request)传给下载器
下载器把资源下载下来,并封装成应答包(Response)
爬虫解析Response
解析出实体(Item),则交给实体管道进行进一步的处理
解析出的是链接(URL),则把URL交给调度器等待抓取
详细流程如下:
1 引擎:Hi!Spider, 你要处理哪一个网站?
2 Spider:老大要我处理xxxx.com。
3 引擎:你把第一个需要处理的URL给我吧。
4 Spider:给你,第一个URL是xxxxxxx.com。
5 引擎:Hi!调度器,我这有request请求你帮我排序入队一下。
6 调度器:好的,正在处理你等一下。
7 引擎:Hi!调度器,把你处理好的request请求给我。
8 调度器:给你,这是我处理好的request
9 引擎:Hi!下载器,你按照老大的下载中间件的设置帮我下载一下这个request请求
10 下载器:好的!给你,这是下载好的东西。(如果失败:sorry,这个request下载失败了。然后引擎告诉调度器,这个request下载失败了,你记录一下,我们待会儿再下载)
11 引擎:Hi!Spider,这是下载好的东西,并且已经按照老大的下载中间件处理过了,你自己处理一下(注意!这儿responses默认是交给def parse()这个函数处理的)
12 Spider:(处理完毕数据之后对于需要跟进的URL),Hi!引擎,我这里有两个结果,这个是我需要跟进的URL,还有这个是我获取到的Item数据。
13 引擎:Hi !管道 我这儿有个item你帮我处理一下!调度器!这是需要跟进URL你帮我处理下。然后从第四步开始循环,直到获取完老大需要全部信息。
14 管道 调度器:好的,现在就做!
4.1.3 Scrapy 开发一般步骤
1、新建项目 (scrapy startproject xxx):新建一个新的爬虫项目
2、明确目标 (编写items.py):明确你想要抓取的目标
3、制作爬虫 (spiders/xxspider.py):制作爬虫开始爬取网页
4、存储内容 (pipelines.py):设计管道存储爬取内容
本实例的流程如下图

4.1.4.Scrapy安装
|
1 |
conda install scrapy |
验证安装是否成功
4.2入门案例
主要步骤:
1、创建一个Scrapy项目
2、定义提取的结构化数据(Item)
3、编写爬取网站的 Spider 并提取出结构化数据(Item)
4、编写 Item Pipelines 来存储提取到的Item(即结构化数据)
4.2.1 创建项目
新建项目(scrapy my_project)
在开始爬取之前,必须创建一个新的Scrapy项目。进入自定义的项目目录中,运行下列命令:
|
1 |
scrapy startproject my_project |
其中, my_project 为项目名称,可以看到将会创建一个 my_project 文件夹,目录结构大致如下:
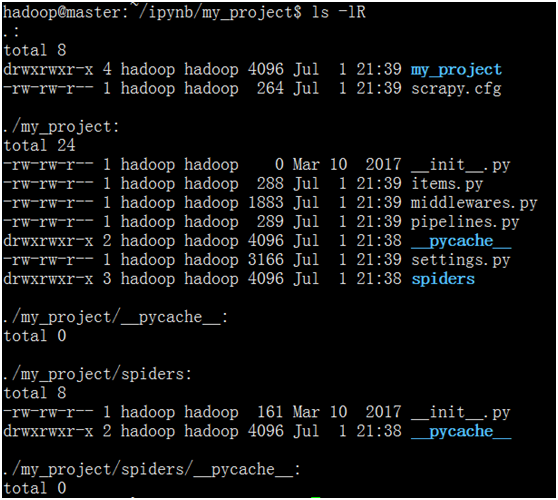
下面来简单介绍一下各个主要文件的作用:
scrapy.cfg 是爬虫执行的入口文件。当输入“scrapy crawl”命令让爬虫开始工作时,首先会读取该文件中的配置项内容。
my_project/items.py 文件定义了爬虫抓取下来的数据,是以何种组织方式存储信息的。比如爬虫抓取的结果可以是标题字符串,也可以是结构化的JSON对象,或者是一张图片对应的字节流,items.py就是用来定义结构化对象中的属性名。
my_project/pipelines.py文件定义了信息的保存方式。爬虫抓取的内容,存放在内存对象中,如何保存这些信息,用户可以定义多种方式,比如写入文件、存入DB或者直接在控制台输出。Scrapy会采用管道(pipeline)方式,把内存中的信息依次交给每个管道文件。
my_project/settings.py 文件保存了爬虫运行时所依赖的配置信息。比如用户定义了两个pipelines.py文件,希望把抓取的内容先写入DB,再输出到控制台,那么就可以在setttings.py文件中定义ITEM_PIPELINES属性,其值分别给出了两个管道文件的文件名。比如:
|
1 |
ITEM_PIPELINES={'page.FilePipelines.PagePipeline':1, 'page.DBPipelines.DBPipeline':2} |
my_project/spiders/ 是用来存放具体爬虫文件的目录。爬虫文件需要用户手动创建,在该目录下可以同时存在多个爬虫文件。
【备注】为保证输出格式为json文件也支持中文,在settings.py添加如下语句:
|
1 |
FEED_EXPORT_ENCODING = 'utf-8' |
4.2.2 明确目标
我们打算抓取:http://www.itcast.cn/channel/teacher.shtml 网站里的所有讲师的姓名、职称和个人信息。打开my_project目录下的items.py
Item 定义结构化数据字段,用来保存爬取到的数据,有点像Python中的dict,但是提供了一些额外的保护减少错误。
可以通过创建一个 scrapy.Item 类, 并且定义类型为
scrapy.Field的类属性来定义一个Item。接下来,创建一个ItcastItem 类,和构建item模型(model)。
|
1 2 3 4 5 |
import scrapy class ItcastItem(scrapy.Item): name = scrapy.Field() title = scrapy.Field() info = scrapy.Field() |
4.2.3 制作爬虫
主要编辑spiders/itcastSpider.py
爬虫功能要分两步:
1. 爬数据
在当前目录下输入命令,将在my_project /spider目录下创建一个名为itcast的爬虫,并指定爬取域的范围:
|
1 |
scrapy genspider itcast "itcast.cn" |
打开 my_project /spider目录里的 itcast.py,默认增加了下列代码:
|
1 2 3 4 5 6 7 8 |
import scrapy class ItcastSpider(scrapy.Spider): name = "itcast" allowed_domains = ["itcast.cn"] start_urls = ('http://www.itcast.cn/') def parse(self, response): pass |
其实也可以由我们自行创建itcast.py并编写上面的代码,只不过使用命令可以免去编写固定代码的麻烦要建立一个Spider, 你必须用scrapy.Spider类创建一个子类,并确定了三个强制的属性 和 一个方法。
name = "" :这个爬虫的识别名称,必须是唯一的,在不同的爬虫必须定义不同的名字。
allow_domains = [] 是搜索的域名范围,也就是爬虫的约束区域,规定爬虫只爬取这个域名下的网页,不存在的URL会被忽略。
start_urls = () :爬取的URL元祖/列表。爬虫从这里开始抓取数据,所以,第一次下载的数据将会从这些urls开始。其他子URL将会从这些起始URL中继承性生成。
parse(self, response) :解析的方法,每个初始URL完成下载后将被调用,调用的时候传入从每一个URL传回的Response对象来作为唯一参数,主要作用如下:
负责解析返回的网页数据(response.body),提取结构化数据(生成item)
生成需要下一页的URL请求。
将start_urls的值修改为需要爬取的第一个url
|
1 |
start_urls = ("http://www.itcast.cn/channel/teacher.shtml",) |
修改parse()方法
|
1 2 3 |
def parse(self, response): filename = "teacher.html" open(filename, 'wb').write(response.body) |
然后运行一下看看,在my_project目录下(含文件scrapy.cfg所在的目录)执行:
|
1 |
scrapy crawl itcast -o teacher.html |
2. 取数据
爬取整个网页完毕,接下来的就是的取过程了,首先观察页面源码:

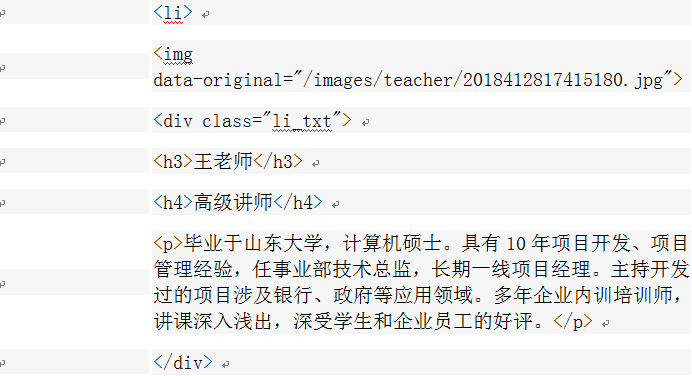
是不是一目了然?直接上XPath开始提取数据吧。
我们之前在my_project /items.py 里定义了一个ItcastItem类。 这里引入进来
|
1 |
from my_project.items import ItcastItem |
然后将我们得到的数据封装到一个 ItcastItem 对象中,可以保存每个老师的属性,修改itcast.py文件如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import scrapy from my_project.items import ItcastItem class ItcastSpider(scrapy.Spider): name = "itcast" allowed_domains = ["itcast.cn"] start_urls = ("http://www.itcast.cn/channel/teacher.shtml",) def parse(self, response): #filename = "teacher.html" #open(filename, 'wb').write(response.body) # 存放老师信息的集合 items = [] for each in response.xpath("//div[@class='li_txt']"): # 将我们得到的数据封装到一个 `ItcastItem` 对象 item = ItcastItem() #extract()方法返回的都是unicode字符串 name = each.xpath("h3/text()").extract() title = each.xpath("h4/text()").extract() info = each.xpath("p/text()").extract() #xpath返回的是包含一个元素的列表 item['name'] = name[0].encode('utf-8') item['title'] = title[0].encode('utf-8') item['info'] = info[0].encode('utf-8') items.append(item) # 直接返回最后数据 return items |
【备注】这里补充一点xpath有关内容,更多内容大家可以通过google或百度查询
XPath 使用路径表达式在 XML 文档中选取节点。节点是通过沿着路径或者 step 来选取的。
下面列出了最有用的路径表达式:

3. 运行
在scrapy.cfg 所在文件的目录下,运行如下命令
|
1 |
scrapy crawl itcast -o teachers.csv |
运行完成后,在当前目录下,将生成一个文件:teachers.csv
查看该文件:

4、修改settles.py文件
一些变量可存放在settles.py文件中,把数据库的连接信息存放在该文件,便于以后维护管理
|
1 2 3 4 5 6 7 8 9 10 11 |
###########connect to mysql info######### MYSQL_HOST = 'slave02' MYSQL_USER = 'feigu' #数据库用户feigu的密码 MYSQL_PASSWORD = 'feigu' MYSQL_PORT = 3306 #你自己数据库的名称 MYSQL_DB = 'testdb' CHARSET = 'utf8' |
5、利用pipeline,把数据导入mysql数据库
pipeline.py文件定义数据存储的方式,此处定义数据存储的逻辑,可以将数据存储加载到MySQL数据库,MongoDB数据库,文件,CSV,Excel等存储介质中,如下以存储载CSV为例。
编辑pipeline.py文件
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# -*- coding: utf-8 -*- # Define your item pipelines here # # Don't forget to add your pipeline to the ITEM_PIPELINES setting # See: http://doc.scrapy.org/en/latest/topics/item-pipeline.html import pymysql import csv from scrapy.utils.project import get_project_settings #下面把抓取数据导出为csv文件 class MyProjectPipeline_csv(object): def process_item(self, item, spider): csvFile = open('/home/hadoop/ipynb/my_project/td_list.csv',mode='a') files = csv.writer(csvFile,delimiter=',') files.writerow([str(item['name'],encoding="utf-8"),str(item['title'],encoding="utf-8"),str(item['info'],encoding="utf-8")]) #files.writerow('\n') return item #下面是将爬取到的信息插入到MySQL数据库中 class MyProjectPipeline_mysql(object): def __init__(self): self.settings = get_project_settings() self.host=self.settings.get('MYSQL_HOST') self.user=self.settings.get('MYSQL_USER') self.pwd=self.settings.get('MYSQL_PASSWORD') self.db=self.settings.get('MYSQL_DB') def process_item(self, item, spider): #数据库连接 con=pymysql.connect(host=self.host,user=self.user,passwd=self.pwd,db=self.db) #数据库游标 cue=con.cursor() print("mysql connect succes")#测试语句,这在程序执行时非常有效的理解程序是否执行到这一步 #sql="insert into tdlist (name,title,info) values(%s,%s,%s)" % (item['name'],item['title'],item['info']) try: cue.execute("insert into teacherlist (name,title,info) values(%s,%s,%s)",[ item['name'],item['title'],item['info']]) print("insert success") except Exception as e: print('Insert error:',e) con.rollback() else: con.commit() con.close() return item |
6、修改settles.py文件
为说明通过pipeline导入数据程序,在文件settings.py后,添加如下一行:
|
1 |
ITEM_PIPELINES = {'my_project.pipelines.MyProjectPipeline_csv': 100,'my_project.pipelines.MyProjectPipeline_mysql': 200} |
7、运行以下命令
|
1 |
scrapy crawl itcast |
8、查询结果
csv文件内容:

查看数据库对应表部分记录:
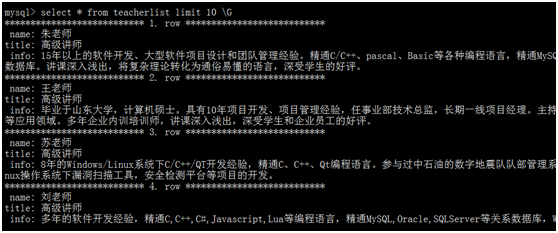


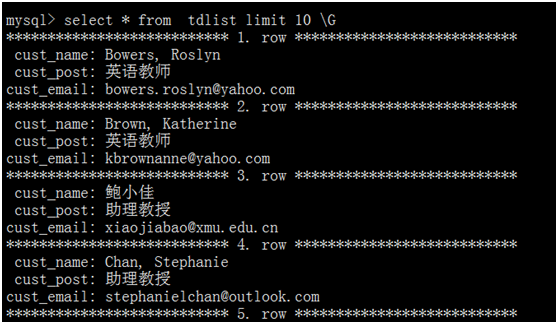













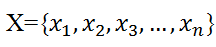
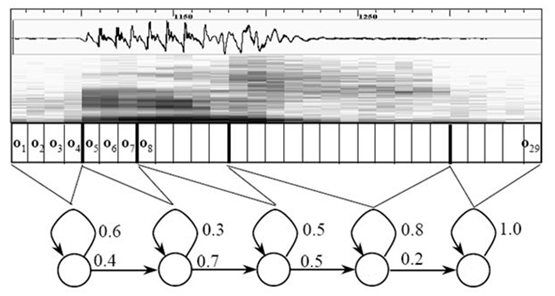
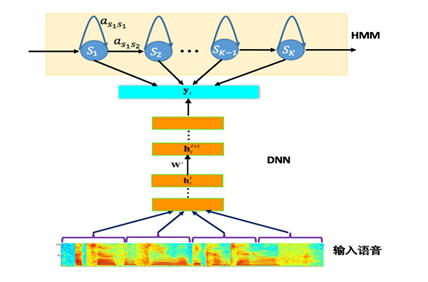
 含义依次类推。
含义依次类推。
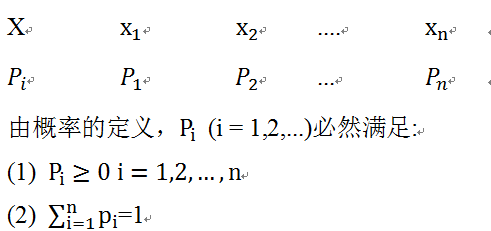

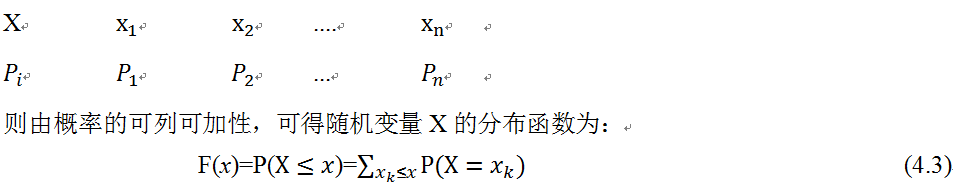
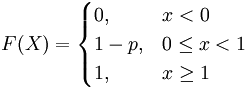


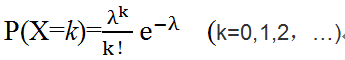




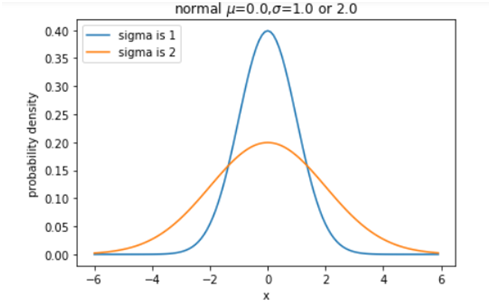
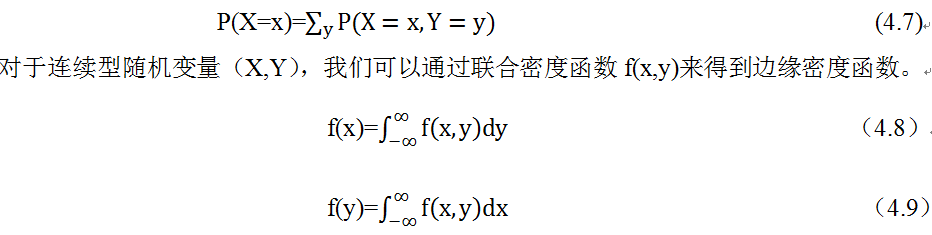
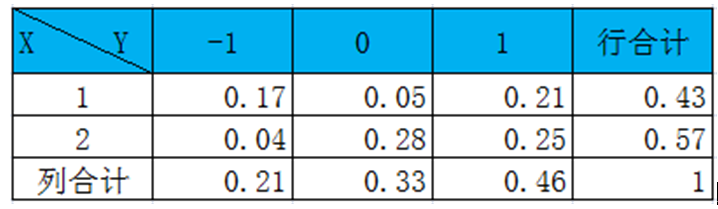


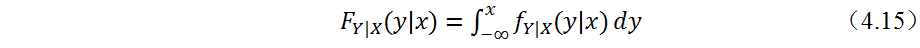
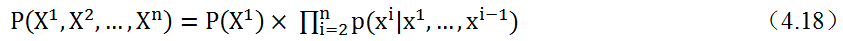


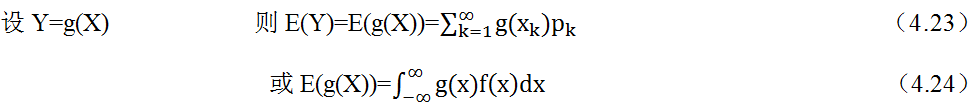
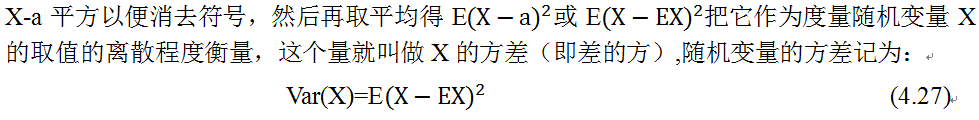

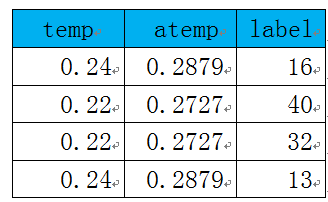
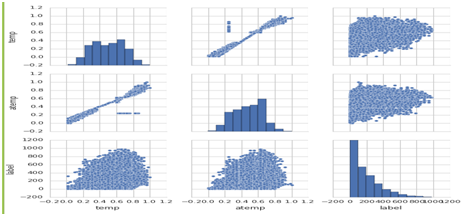

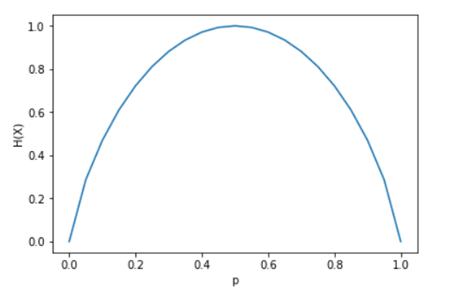
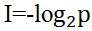 。为此,可能有人会问,为何要用对数,前面还要带上负号?
。为此,可能有人会问,为何要用对数,前面还要带上负号?