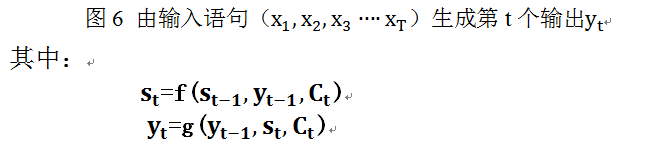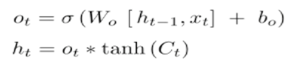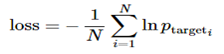第17章 自己动手做一个聊天机器人
【环境说明】
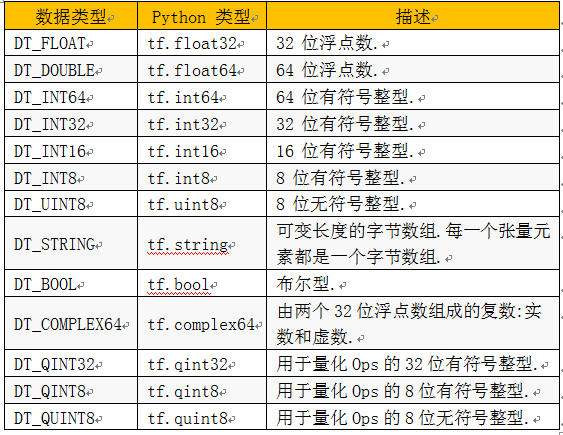
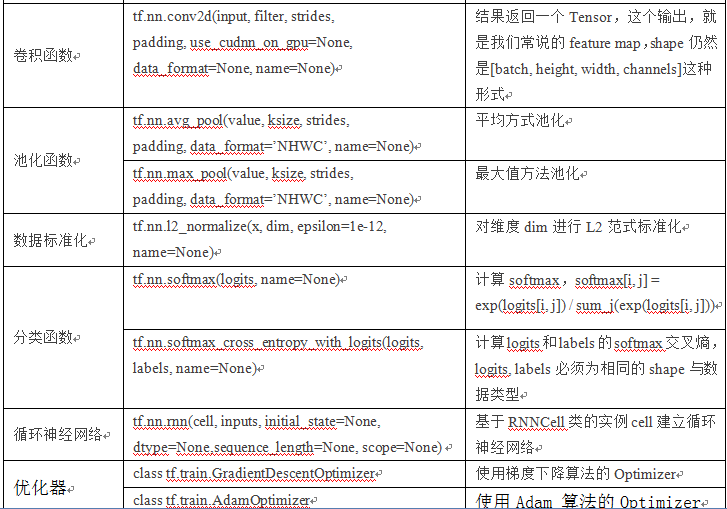
使用Python3.6的Jupyter,TensorFlow1.3+, tensorflow的embedding_attention_seq2seq,使用LSTM神经网络,采用AdamOptimizer优化器、jieba分词等。
17.1 聊天机器人简介
现在很多公司把技术重点放在人机对话上,通过人机对话,控制各种家用电器、控制机器人、控制汽车等等。如,苹果的Siri、微软的小冰、百度的度秘、亚马逊的蓝色音箱等等。这种智能聊天机器人将给企业带来强大的竞争优势。
智能聊天机器人的发展经历了3代不同的技术:
1)第一代,基于逻辑判断,如if then;else then等;
2)第二代,基于检索库,如给定一个问题,然后从检索库中找到与之匹配度最高的答案;
3)第三代,基于深度学习,采用seq2seq+Attention模型,经过大量数据的训练和学习,得到一个模型,通过这个模型,输入数据产生相应的输出。接下来我们通过一个简单实例来介绍seq2seq+Attention模型的架构及原理。
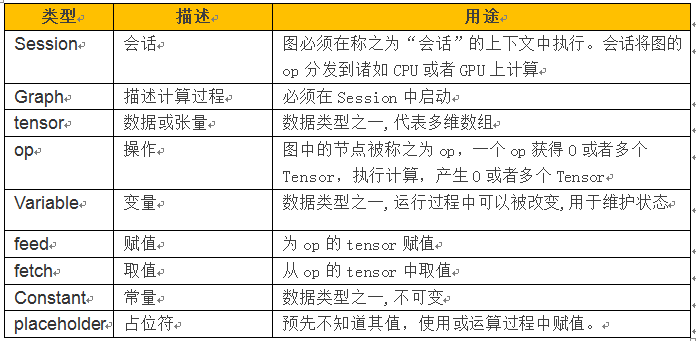
17.2 聊天机器人的原理
目前聊天机器人一般采用带注意力(Attention)的模型,但之前一般采用Seq2Seq模型,这种模型有哪些不足?需要引入Attention Model(简称为 AM)呢?我们先来看一下Seq2Seq模型的架构,如下图:
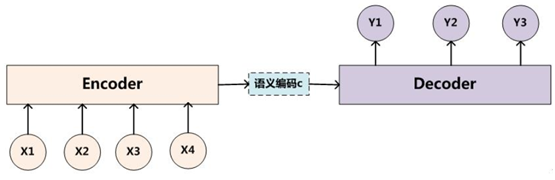
图1 ncoder-Decoder 架构
这是一个典型的编码器-解码器(Encoder-Decoder)框架。我们该如何理解这个框架呢?
从左到右,我们可以这么直观地去理解:从左到右,看作适合处理由一个句子(或篇章)生成另外一个句子(或篇章)的通用处理模型。假设这句子对为<X,Y>,我们的目标是给定输入句子X,期待通过Encoder-Decoder框架来生成目标句子Y。X和Y可以是同一种语言,也可以是两种不同的语言。而X和Y分别由各自的单词序列构成:
 每个
每个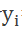 都依次这么产生,那么看起来就是整个系统根据输入句子X生成了目标句子Y。
都依次这么产生,那么看起来就是整个系统根据输入句子X生成了目标句子Y。
Encoder-Decoder是个非常通用的计算框架,至于Encoder和Decoder具体使用什么模型是由我们自己定的,常见的比如CNN/RNN/BiRNN/GRU/LSTM/Deep LSTM等,而且变化组合非常多。
Encoder-Decoder模型应用非常广泛,其应用场景非常多,比如对于机器翻译来说,<X,Y>就是对应不同语言的句子,比如X是英语句子,Y是对应的中文句子翻译。再比如对于文本摘要来说,X就是一篇文章,Y就是对应的摘要;再比如对于对话机器人来说,X就是某人的一句话,Y就是对话机器人的应答;再比如……总之,太多了。
这个框架有一个缺点,就是生成的句子中每个词采用的中间语言编码是相同的,都是C,具体看如下表达式。这种框架,在句子表较短时,性能还可以,但句子稍长一些,生成的句子就不尽如人意了。如何解决这一不足呢?
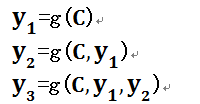
解铃还须系铃人,既然问题出在C上,所以我们需要在C上做文章。我们引入一个Attention机制,可以有效解决这个问题。
17.3 带注意力的框架

这就是为何说这个模型没有体现出注意力的缘由。这类似于你看到眼前的画面,但是没有注意焦点一样。
如果拿机器翻译(输入英文输出中文)来解释这个分心模型的Encoder-Decoder框架更好理解,比如:
输入英文句子:Tom chase Jerry,Encoder-Decoder框架逐步生成中文单词:“汤姆”,“追逐”,“杰瑞”
在翻译“杰瑞”这个中文单词的时候,分心模型里面的每个英文单词对于翻译目标单词“杰瑞”贡献是相同的,很明显这里不太合理,显然“Jerry”对于翻译成“杰瑞”更重要,但是分心模型是无法体现这一点的,这就是为何说它没有引入注意力的原因。
没有引入注意力的模型在输入句子比较短的时候估计问题不大,但是如果输入句子比较长,此时所有语义完全通过一个中间语义向量来表示,单词自身的信息已经消失,可想而知会丢失很多细节信息,这也是为何要引入注意力模型的重要原因。
上面的例子中,如果引入AM(Attention Model)模型的话,应该在翻译“杰瑞”的时候,体现出英文单词对于翻译当前中文单词不同的影响程度,比如给出类似下面一个概率分布值:
(Tom,0.3)(Chase,0.2)(Jerry,0.5)
每个英文单词的概率代表了翻译当前单词“杰瑞”时,注意力分配模型分配给不同英文单词的注意力大小。这对于正确翻译目标语单词肯定是有帮助的,因为引入了新的信息。同理,目标句子中的每个单词都应该学会其对应的源语句子中单词的注意力分配概率信息。这意味着在生成每个单词Yi的时候,原先都是相同的中间语义表示C会替换成根据当前生成单词而不断变化的Ci。理解AM模型的关键就是这里,即由固定的中间语义表示C换成了根据当前输出单词来调整成加入注意力模型的变化的Ci。增加了AM模型的Encoder-Decoder框架理解起来如图2所示。
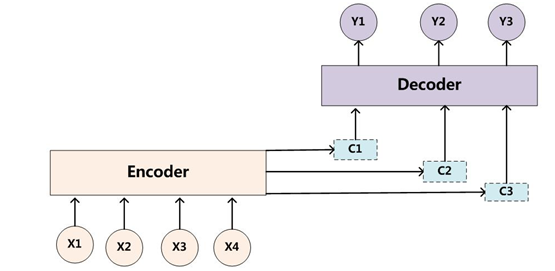
图2 引入AM(Attention Model)模型的Encoder-Decoder框架
即生成目标句子单词的过程成了下面的形式:
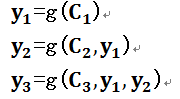
而每个Ci可能对应着不同的源语句子单词的注意力分配概率分布,比如对于上面的英汉翻译来说,其对应的信息可能如下:

其中,f2函数代表Encoder对输入英文单词的某种变换函数,比如如果Encoder是用的RNN模型的话,这个f2函数的结果往往是某个时刻输入xi后隐层节点的状态值;g代表Encoder根据单词的中间表示合成整个句子中间语义表示的变换函数,一般的做法中,g函数就是对构成元素加权求和,也就是常常在论文里看到的下列公式:
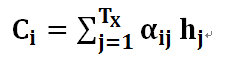

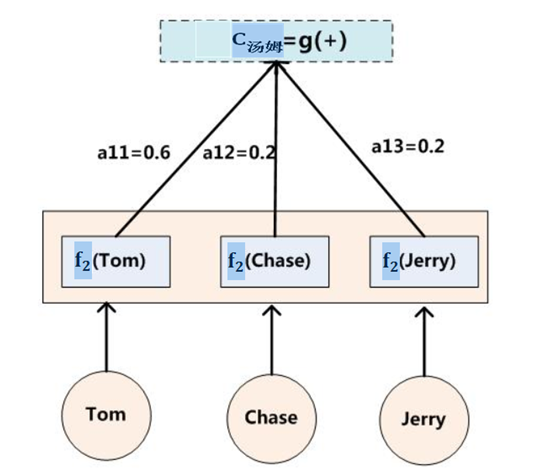
图3 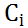 的生成过程
的生成过程
这里还有一个问题:生成目标句子某个单词,比如“汤姆”的时候,你怎么知道AM模型所需要的输入句子单词注意力分配概率分布值呢?就是说“汤姆”对应的概率分布:
(Tom,0.6)(Chase,0.2)(Jerry,0.2)
如何得到的呢?
为了便于说明,我们假设对图1的非AM模型的Encoder-Decoder框架进行细化,Encoder采用RNN模型,Decoder也采用RNN模型,这是比较常见的一种模型配置,则图1的图转换为下图:
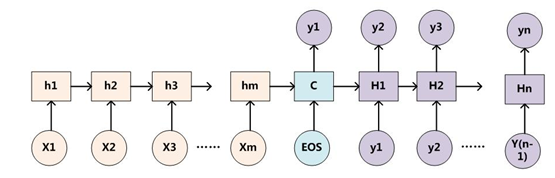
图4 RNN作为具体模型的Encoder-Decoder框架
那么用下图可以较为便捷地说明注意力分配概率分布值的通用计算过程:
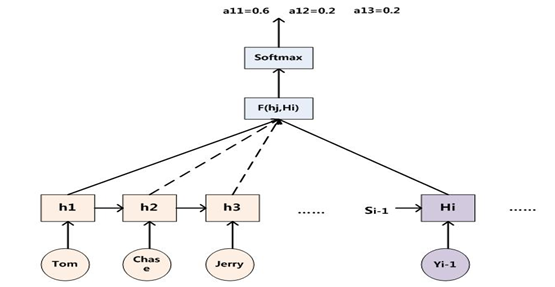
图5 AM注意力分配概率计算
相当于在原来的模型上,又加了一个单层DNN(特指全连接)网络,当前输出词Yi针对某一个输入词j的注意力权重由当前的隐层Hi,以及输入词j的隐层状态(hj)共同决定;函数F(hj,Hi)在不同论文里可能会采取不同的方法,然后函数F的输出经过Softmax进行归一化就得到得到一个0-1的注意力分配概率分布数值。
如图5所示:当输出单词为“汤姆”时刻对应的输入句子单词的对齐概率。绝大多数AM模型都是采取上述的计算框架来计算注意力分配概率分布信息,区别只是在F的定义上可能有所不同。yi值的生成可参考下图6:

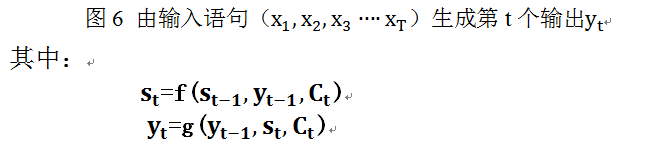
上述内容就是论文里面常常提到的Soft Attention Model的基本思想,你能在文献里面看到的大多数AM模型基本就是这个模型,区别很可能只是把这个模型用来解决不同的应用问题。那么怎么理解AM模型的物理含义呢?一般文献里会把AM模型看作是单词对齐模型,这是非常有道理的。目标句子生成的每个单词对应输入句子单词的概率分布可以理解为输入句子单词和这个目标生成单词的对齐概率,这在机器翻译语境下是非常直观的:传统的统计机器翻译一般在做的过程中会专门有一个短语对齐的步骤,而注意力模型其实起的是相同的作用。在其他应用里面把AM模型理解成输入句子和目标句子单词之间的对齐概率也是很顺畅的想法。
当然,从概念上理解的话,把AM模型理解成影响力模型也是合理的,就是说生成目标单词的时候,输入句子每个单词对于生成这个单词有多大的影响程度。这种想法也是比较好理解AM模型物理意义的一种思维方式。
图7是论文“A Neural Attention Model for Sentence Summarization”中,Rush用AM模型来做生成式摘要给出的一个AM的一个非常直观的例子。

图7 句子生成式摘要例子
这个例子中,Encoder-Decoder框架的输入句子是:“russian defense minister ivanov called sunday for the creation of a joint front for combating global terrorism”。对应图中纵坐标的句子。系统生成的摘要句子是:“russia calls for joint front against terrorism”,对应图中横坐标的句子。可以看出模型已经把句子主体部分正确地抽出来了。矩阵中每一列代表生成的目标单词对应输入句子每个单词的AM分配概率,颜色越深代表分配到的概率越大。这个例子对于直观理解AM是很有帮助作用的。
17.4 用TensorFlow的seq2seq+Attention制作你自己的聊天机器人
上节我们介绍了带AM的seq2seq模型的框架及原理,这一节我们将利用tensorflow实行一个非常简单的功能,两个奇数序列样本,输出也是奇数序列,以此建立一个简单encode-decode模型,这里我们将使用TensorFlow提供的强大API,不过要真正利用好tensorflow必须理解好它的重要接口及其所有参数,所以第一步我们找到这次要使用的最关键的接口embedding_attention_seq2seq。
embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs,
cell,
num_encoder_symbols,
num_decoder_symbols,
embedding_size,
num_heads=1,
output_projection=None,
feed_previous=False,
dtype=None,
scope=None,
initial_state_attention=False
)
在这个接口函数中有很多参数,这些参数的具体含义是啥?如何使用这些参数?这些问题我们在下节将详细说明。
17.4.1 接口参数说明
为了更好理解这个接口,我们参考上节的图6,以下我们就上节这个接口函数各参数进行详细说明:
1)encoder_inputs
参数encoder_inputs是一个list,list中每一项是1D(1维)的Tensor,这个Tensor的shape是[batch_size],Tensor中每一项是一个整数,类似这样:
[array([0, 0, 0, 0], dtype=int32),
array([0, 0, 0, 0], dtype=int32),
array([8, 3, 5, 3], dtype=int32),
array([7, 8, 2, 1], dtype=int32),
array([6, 2, 10, 9], dtype=int32)]
其中5个array,表示一句话的长度是5个词,每个array里有4个数,表示batch是4,也就是一共4个样本。那么可以看出第一个样本是[[0],[0],[8],[7],[6]],第二个样本是[[0],[0],[3],[8],[2]],以此类推。这里的数字是用来区分不同词的一个id,一般通过统计得出,一个id表示一个词
2)decoder_inputs
同理,参数decoder_inputs也是和encoder_inputs一样结构,不赘述。
3)cell
参数cell是tf.nn.rnn_cell.RNNCell类型的循环神经网络单元,可以用tf.contrib.rnn.BasicLSTMCell、tf.contrib.rnn.GRUCell等。
4)num_encoder_symbols
参数num_encoder_symbols是一个整数,表示encoder_inputs中的整数词id的数目。
5)num_decoder_symbols
同理num_decoder_symbols表示decoder_inputs中整数词id的数目。
6)embedding_size
参数embedding_size表示在内部做word embedding(如通过word2vec把各单词转换为向量)时转成几维向量,需要和RNNCell的size大小相等。
7)num_heads
参数num_heads表示在attention_states中的抽头数量,一般取1。
8)output_projection
参数output_projection是一个(W, B)结构的元组(tuple),W是shape为[output_size x num_decoder_symbols]的权重(weight)矩阵,B是shape为[num_decoder_symbols]的偏置向量,那么每个RNNCell的输出经过WX+B就可以映射成num_decoder_symbols维的向量,这个向量里的值表示的是任意一个decoder_symbol的可能性,也就是softmax的输出值。
9)feed_previous
参数feed_previous表示decoder_inputs是我们直接提供训练数据的输入,还是用前一个RNNCell的输出映射出来的,如果feed_previous为True,那么就是用前一个RNNCell的输出,并经过WX+B映射而成。
10)dtype
参数dtype是RNN状态数据的类型,默认是tf.float32。
11)scope
scope是子图的命名,默认是“embedding_attention_seq2seq”
12)initial_state_attention
initial_state_attention表示是否初始化attentions,默认为否,表示全都初始化为0
函数的返回值是一个(outputs, state)结构的tuple,其中outputs是一个长度为句子长度(词数,与上面encoder_inputs的list长度一样)的list,list中每一项是一个2D(二维)的tf.float32类型的Tensor,第一维度是样本数,比如4个样本则有四组Tensor,每个Tensor长度是embedding_size,像下面的样子:
[
array([
[-0.02027004, -0.017872 , -0.00233014, -0.0437047 , 0.00083584,
0.01339234, 0.02355197, 0.02923143],
[-0.02027004, -0.017872 , -0.00233014, -0.0437047 , 0.00083584,
0.01339234, 0.02355197, 0.02923143],
[-0.02027004, -0.017872 , -0.00233014, -0.0437047 , 0.00083584,
0.01339234, 0.02355197, 0.02923143],
[-0.02027004, -0.017872 , -0.00233014, -0.0437047 , 0.00083584,
0.01339234, 0.02355197, 0.02923143]
],dtype=float32),
array([
......
],dtype=float32),
array([
......
],dtype=float32),
array([
......
],dtype=float32),
array([
......
],dtype=float32),
]
其实这个outputs可以描述为5*4*8个浮点数,5是句子长度,4是样本数,8是词向量维数。
下面再看返回的state,它是num_layers个LSTMStateTuple组成的大tuple,这里num_layers是初始化cell时的参数,表示神经网络单元有几层,一个由2层LSTM神经元组成的encoder-decoder多层循环神经网络是像下面这样的网络结构:
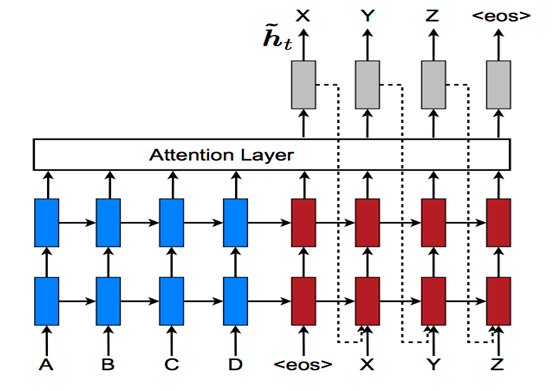
图8 由2层LSTM神经元组成的encoder-decoder多层循环神经网络
encoder_inputs输入encoder的第一层LSTM神经元,这个神经元的output传给第二层LSTM神经元,第二层的output再传给Attention层,而encoder的第一层输出的state则传给decoder第一层的LSTM神经元,依次类推,如图8所示。
回过头来再看LSTM State Tuple这个结构,它是由两个Tensor组成的tuple,第一个tensor命名为c,由4个8维向量组成(4是batch, 8是state_size也就是词向量维度), 第二个tensor命名为h,同样由4个8维向量组成。
这里的c和h如下所示:
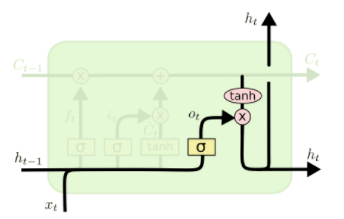
c是传给下一个时序的存储数据,h是隐藏层的输出,这里的计算公式是:
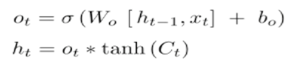
在tensorflow代码里也有对应的实现:
concat = _linear([inputs, h], 4 * self._num_units, True)
i, j, f, o = array_ops.split(value=concat, num_or_size_splits=4, axis=1)
new_c = (c * sigmoid(f + self._forget_bias) + sigmoid(i) * self._activation(j))
new_h = self._activation(new_c) * sigmoid(o)
事实上,如果我们直接使用embedding_attention_seq2seq来做训练,返回的state一般是用不到的。
17.4.2 用数字样本训练seq2seq模型
17.4.2.1预定义seq2seq模型
我们以1、3、5、7、9……奇数序列为例来构造样本,比如两个样本是[[1,3,5],[7,9,11]]和[[3,5,7],[9,11,13]],相当于两个<X,Y>对:
train_set = [[[1, 3, 5], [7, 9, 11]], [[3, 5, 7], [9, 11, 13]]]
输入:[1, 3, 5],输出为:[7, 9, 11]
输入:[3, 5, 7],输出为:[9, 11, 13]
从这两个样本可以看出,输出的每个数据是对应输入加6得到。
为了我们能够满足不同长度的序列,需要让我们训练的序列比样本的序列长度要长一些,比如我们设置为5,即
input_seq_len = 5
output_seq_len = 5
因为样本长度小于训练序列的长度,所以我们用0来填充,即:
那么我们的第一个样本的encoder_input就是:
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0])) + train_set[0][0]
结果为:[0, 0, 1, 3, 5]
那么我们的第二个样本的encoder_input就是:
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0])) + train_set[1][0]
结果为:[0, 0, 3, 5, 7]
ecoder_input我们需要用一个GO_ID来作为起始,再输入样本序列,最后再用PAD_ID来填充,即:
GO_ID = 1
decoder_input_0 = [GO_ID] + train_set[0][1]+[PAD_ID] * (output_seq_len - len(train_set[0][1]) - 1)
decoder_input_1 = [GO_ID] + train_set[1][1]+[PAD_ID] * (output_seq_len - len(train_set[1][1]) - 1)
print(decoder_input_0,decoder_input_1)
输出结果为:[1, 7, 9, 11, 0] [1, 9, 11, 13, 0]
为了把输入转成上面讲到的embedding_attention_seq2seq中的输入参数encoder_inputs和decoder_inputs的格式,我们进行如下转换即可:
import numpy as np
encoder_inputs = []
decoder_inputs = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
运算结果如下:
encoder_inputs为:
[array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs为:
[array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
太好了,第一步大功告成,我们把这部分独立出一个函数,整理代码如下:
import numpy as np
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
def get_samples():
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
"""
train_set = [[[1, 3, 5], [7, 9, 11]], [[3, 5, 7], [9, 11, 13]]]
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0]))+ train_set[0][0]
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0]))+ train_set[1][0]
decoder_input_0 = [GO_ID] + train_set[0][1]+ [PAD_ID] * (output_seq_len - len(train_set[0][1]) - 1)
decoder_input_1 = [GO_ID] + train_set[1][1]+ [PAD_ID] * (output_seq_len - len(train_set[1][1]) - 1)
encoder_inputs = []
decoder_inputs = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
return encoder_inputs, decoder_inputs
完成上面这部分之后,我们开始构造模型,我们了解了tensorflow的运行过程是先构造图,再加入数据计算的,所以我们构建模型的过程实际上就是构建一张图。具体步骤如下:
1)创建encoder_inputs和decoder_inputs的placeholder(占位符):
import tensorflow as tf
encoder_inputs = []
decoder_inputs = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
2)创建一个记忆单元数目为size=8的LSTM神经元结构:
size = 8
cell = tf.contrib.rnn.BasicLSTMCell(size)
我们假设我们要训练的奇数序列最大数值是输入最大为10,输出最大为16,那么
num_encoder_symbols = 10
num_decoder_symbols = 16
3)把参数传入embedding_attention_seq2seq获取output
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=False,
dtype=tf.float32)
4)为了说明之后的操作,我们先把这部分运行一下,看看输出的output是个什么样的数据,我们先把上面的构建模型部分放到一个单独的函数里,如下:
def get_model():
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs,
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=False,
dtype=tf.float32)
return encoder_inputs, decoder_inputs, outputs
5)构造运行时的session,并填入样本数据:
tf.reset_default_graph()
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs = get_samples()
encoder_inputs, decoder_inputs, outputs = get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
sess.run(tf.global_variables_initializer())
outputs = sess.run(outputs, input_feed)
print(outputs)
输出结果为:
[array([[ 0.02211747, 0.02335669, 0.20193386, 0.13999327, -0.08593997,
0.22940636, -0.01699461, -0.13609734, 0.0205682 , 0.04478336,
-0.06487859, 0.12278311, 0.25824267, -0.11856561, 0.00924652,
-0.05683991],
[-0.07845577, -0.02809871, 0.18017495, 0.0934044 , 0.03219789,
0.07012151, 0.03865771, 0.00123758, 0.07511085, 0.01999556,
-0.02662061, 0.10624584, 0.20883667, -0.02273149, 0.00469023,
-0.05817863]], dtype=float32),
array([[ 0.0059285 , 0.01392498, 0.14229313, 0.07545042, 0.00946952,
0.18953349, 0.00642931, -0.15386952, 0.01010698, 0.01384872,
-0.00726009, 0.13510276, 0.16494165, -0.08263297, 0.01707343,
-0.03762008],
[-0.07017908, -0.04930218, 0.14285906, 0.05723355, 0.06988001,
0.04076997, 0.05316475, -0.0261047 , 0.06291211, 0.01883025,
0.0061325 , 0.12620246, 0.16149819, -0.01529151, 0.050455 ,
-0.03946743]], dtype=float32),
array([[-0.00194316, -0.01631381, 0.1203991 , 0.06203739, 0.03219883,
0.14352044, 0.03928373, -0.14056513, 0.00291529, 0.01727359,
0.01229408, 0.15131217, 0.14297011, -0.0548197 , 0.05326709,
-0.02463808],
[-0.04386059, -0.05562492, 0.10245109, 0.0426993 , 0.09483594,
0.03656092, 0.0556438 , -0.07965589, 0.04327345, 0.01180707,
0.01022344, 0.14290853, 0.1213765 , -0.02787331, 0.10306676,
0.00820766]], dtype=float32),
array([[ 0.01521008, -0.03012705, 0.09070239, 0.05803963, 0.05991809,
0.12920979, 0.06138738, -0.17233956, -0.01331626, 0.01376779,
0.01249342, 0.1820184 , 0.11310001, -0.04977838, 0.10077294,
0.0205139 ],
[-0.04125331, -0.06516436, 0.11274034, 0.04927413, 0.07295317,
0.03652341, 0.03664432, -0.05592719, 0.06112453, 0.02948697,
0.02171964, 0.13186185, 0.1393885 , -0.00982405, 0.09507501,
-0.03440713]], dtype=float32),
array([[-0.0036198 , -0.03023063, 0.08077027, 0.01246183, 0.09018619,
0.10092171, 0.06540067, -0.13675798, -0.0074318 , 0.00661841,
0.0476986 , 0.1658352 , 0.08331098, -0.02784023, 0.07896069,
0.00924372],
[-0.05942168, -0.05818485, 0.09542555, -0.00622959, 0.10408131,
0.01689048, 0.03596107, -0.03097581, 0.06668746, 0.01272842,
0.05121479, 0.11581403, 0.10105841, 0.00028773, 0.07818841,
-0.03244215]], dtype=float32)]
我们看到这里输出的outputs是由5个array组成的list(5是序列长度),每个array由两个size是16的list组成(2表示2个样本,16表示输出符号有16个)
这里的outputs实际上应该对应seq2seq的输出,也就是下图中的W、X、Y、Z、EOS,也就是decoder_inputs[1:],也就是我们样本里的[7,9,11]和[9,11,13]
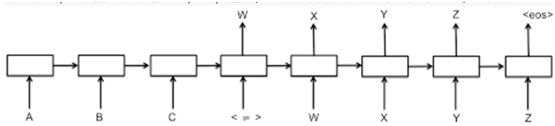
但是我们的decoder_inputs的结构是这样的:
[array([1, 1], dtype=int32), array([ 7, 29], dtype=int32), array([ 9, 31], dtype=int32), array([11, 33], dtype=int32), array([0, 0], dtype=int32)]
与这里的outputs稍有不同,所以不是直接的对应关系,那么到底是什么关系呢?我们先来看一个损失函数的说明:
sequence_loss(
logits,
targets,
weights,
average_across_timesteps=True,
average_across_batch=True,
softmax_loss_function=None,
name=None
)
这个函数的原理可以看成为如下公式(损失函数,目标词语的平均负对数概率最小):
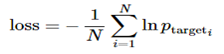
其中logits是一个由多个2D的shape为[batch * num_decoder_symbols]的Tensor组成的list,我们这里batch就是2,num_decoder_symbols就是16,这里组成list的Tensor的个数是output_seq_len,所以我们刚才得到的outputs刚好符合。
其中targets是一个和logits一样长度(output_seq_len)的list,list里每一项是一个整数组成的1D的Tensor,每个Tensor的shape是[batch],数据类型是tf.int32,这刚好和我们的decoder_inputs[1:]也就是刚才说的W、X、Y、Z、EOS结构一样。
其中weights是一个和targets结构一样,只是数据类型是tf.float32。
所以这个函数就是用来计算加权交叉熵损失的,这里面的weights我们需要初始化他的占位符,如下:
target_weights = []
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
那么我们计算得出的损失值就是:
targets = [decoder_inputs[i + 1] for i in range(len(decoder_inputs) - 1)]
print(len(targets))
#loss = seq2seq.sequence_loss(outputs, targets, target_weights)
看到这里,其实我们遇到一个问题,这里的targets长度(为4)比decoder_inputs少了一个,为了让长度保持一致,需要我们对前面decoder_inputs的初始化做个调整,把长度加1。
那么问题来了,这里我们多了一个target_weights这个placeholder,那么我们用什么数据来填充这个占位符呢?因为我们要计算的是加权交叉熵损失,也就是对于有意义的数权重大,无意义的权重小,所以我们把targets中有值的赋值为1,没值的赋值为0,所有代码整理后如下:
# coding:utf-8
import numpy as np
import tensorflow as tf
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
# LSTM神经元size
size = 8
# 最大输入符号数
num_encoder_symbols = 10
# 最大输出符号数
num_decoder_symbols = 16
def get_samples():
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
"""
train_set = [[[1, 3, 5], [7, 9, 11]], [[3, 5, 7], [9, 11, 13]]]
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0]))+ train_set[0][0]
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0]))+ train_set[1][0]
decoder_input_0 = [GO_ID] + train_set[0][1]+ [PAD_ID] * (output_seq_len - len(train_set[0][1]) - 1)
decoder_input_1 = [GO_ID] + train_set[1][1]+ [PAD_ID] * (output_seq_len - len(train_set[1][1]) - 1)
encoder_inputs = []
decoder_inputs = []
target_weights = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
target_weights.append(np.array([
0.0 if length_idx == output_seq_len - 1
or decoder_input_0[length_idx] == PAD_ID else 1.0,
0.0 if length_idx == output_seq_len - 1
or decoder_input_1[length_idx] == PAD_ID else 1.0,
], dtype=np.float32))
return encoder_inputs, decoder_inputs, target_weights
def get_model():
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=False,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
return encoder_inputs, decoder_inputs, target_weights, outputs, loss
def main():
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss = get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
sess.run(tf.global_variables_initializer())
loss = sess.run(loss, input_feed)
print(loss)
if __name__ == "__main__":
tf.reset_default_graph() ##清除默认图的堆栈,并设置全局图为默认图。
main()
运行结果为:2.81352
到这里远远没有结束,我们的旅程才刚刚开始,下面是怎么训练这个模型,
17.4.2.2训练模型
1)首先我们需要经过多轮计算让这里的loss变得很小,这就需要运用梯度下降来更新参数,我们先来看一下tensorflow提供给我们的梯度下降的类:
Class GradientDescentOptimizer的构造方法如下:
__init__(
learning_rate,
use_locking=False,
name='GradientDescent'
)
其中关键就是第一个参数:学习率learning_rate
他的另外一个方法是计算梯度
compute_gradients(
loss,
var_list=None,
gate_gradients=GATE_OP
aggregation_method=None,
colocate_gradients_with_ops=False,
grad_loss=None
)
其中关键参数loss就是传入的误差值,他的返回值是(gradient, variable)组成的list。
再看另外一个方法是更新参数:
apply_gradients(
grads_and_vars,
global_step=None,
name=None
)
其中grads_and_vars就是compute_gradients的返回值。
那么根据loss计算梯度并更新参数的方法如下:
learning_rate = 0.1
opt = tf.train.GradientDescentOptimizer(learning_rate)
update = opt.apply_gradients(opt.compute_gradients(loss))
所以,我们把get_model()增加以上三行,具体如下:
def get_model():
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=False,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
learning_rate = 0.1
opt = tf.train.GradientDescentOptimizer(learning_rate)
update = opt.apply_gradients(opt.compute_gradients(loss))
return encoder_inputs, decoder_inputs, target_weights, outputs, loss,update
我们对main函数增加个循环迭代,具体如下:
def main():
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update= get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
sess.run(tf.global_variables_initializer())
while True:
[loss_ret, _] = sess.run([loss, update], input_feed)
print(loss_ret)
修改后,完整程序如下:
import numpy as np
import tensorflow as tf
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
# LSTM神经元size
size = 8
# 最大输入符号数
num_encoder_symbols = 10
# 最大输出符号数
num_decoder_symbols = 16
def get_samples():
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
"""
train_set = [[[1, 3, 5], [7, 9, 11]], [[3, 5, 7], [9, 11, 13]]]
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0]))+ train_set[0][0]
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0]))+ train_set[1][0]
decoder_input_0 = [GO_ID] + train_set[0][1]+ [PAD_ID] * (output_seq_len - len(train_set[0][1]) - 1)
decoder_input_1 = [GO_ID] + train_set[1][1]+ [PAD_ID] * (output_seq_len - len(train_set[1][1]) - 1)
encoder_inputs = []
decoder_inputs = []
target_weights = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
target_weights.append(np.array([
0.0 if length_idx == output_seq_len - 1
or decoder_input_0[length_idx] == PAD_ID else 1.0,
0.0 if length_idx == output_seq_len - 1
or decoder_input_1[length_idx] == PAD_ID else 1.0,
], dtype=np.float32))
return encoder_inputs, decoder_inputs, target_weights
def get_model():
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=False,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
learning_rate = 0.1
opt = tf.train.GradientDescentOptimizer(learning_rate)
update = opt.apply_gradients(opt.compute_gradients(loss))
return encoder_inputs, decoder_inputs, target_weights, outputs, loss,update
def main():
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update= get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
sess.run(tf.global_variables_initializer())
#循环2000次
for step in range(2000):
[loss_ret, _] = sess.run([loss, update], input_feed)
if step%100 ==0:
print(loss_ret)
if __name__ == "__main__":
tf.reset_default_graph()
main()
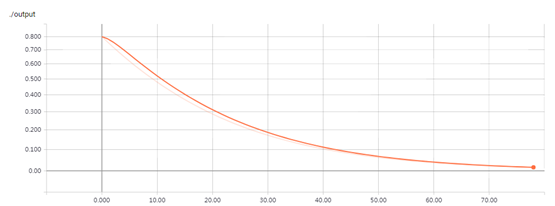
再次运行代码后,我们看到loss_ret唰唰的收敛,如下:
2.84531
0.870862
0.297892
0.0739714
0.0334021
0.0200548
0.0137981
0.0102763
0.0080602
0.0065568
0.00548026
0.00467716
0.00405862
0.00356976
0.00317507
0.00285076
0.00258015
0.00235146
0.00215595
0.0019872
看来我们的训练结果还不错,接下来就是实现预测的逻辑了,就是我们只输入样本的encoder_input,看能不能自动预测出decoder_input。
17.4.2.3测试模型
1)在对新数据进行预测之前,我们需要把训练好的模型保存起来,以便重新启动做预测时能够加载:
def get_model():
...
saver = tf.train.Saver(tf.global_variables())
return ..., saver
在训练结束后执行
saver.save(sess, './model/chatbot/demo')
这样模型会存储到./model目录下以demo开头的一些文件中,之后我们要加载时就先调用:
saver.restore(sess, './model/chatbot/demo')
2)因为我们在做预测的时候,原则上不能有decoder_inputs输入了,所以在执行时的decoder_inputs就要取前一个时序的输出,这时候embedding_attention_seq2seq的feed_previous参数就派上用场了,这个参数的含义就是:若为True则decoder里每一步输入都用前一步的输出来填充,如下图:

所以,我们的get_model需要传递参数来区分训练和预测可通过不同的feed_previous配置,另外,考虑到预测时main函数也是不同的,索性我们分开两个函数来分别做train和predict,整理好的一份完整代码如下(为了更好理解,完整代码和上面稍有出入,请以这份代码为准):
import numpy as np
import tensorflow as tf
import os
import sys
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
output_dir='./model/chatbot/demo'
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
# 结尾标记
EOS_ID = 2
# LSTM神经元size
size = 8
# 最大输入符号数
num_encoder_symbols = 10
# 最大输出符号数
num_decoder_symbols = 16
# 学习率
learning_rate = 0.1
def get_samples():
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
"""
train_set = [[[1, 3, 5], [7, 9, 11]], [[3, 5, 7], [9, 11, 13]]]
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0]))+ train_set[0][0]
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0]))+ train_set[1][0]
decoder_input_0 = [GO_ID] + train_set[0][1]+ [EOS_ID] * (output_seq_len - len(train_set[0][1]) - 1)
decoder_input_1 = [GO_ID] + train_set[1][1]+ [EOS_ID] * (output_seq_len - len(train_set[1][1]) - 1)
encoder_inputs = []
decoder_inputs = []
target_weights = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
target_weights.append(np.array([
0.0 if length_idx == output_seq_len - 1
or decoder_input_0[length_idx] == PAD_ID else 1.0,
0.0 if length_idx == output_seq_len - 1
or decoder_input_1[length_idx] == PAD_ID else 1.0,
], dtype=np.float32))
return encoder_inputs, decoder_inputs, target_weights
def get_model(feed_previous=False):
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=feed_previous,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
# 梯度下降优化器
opt = tf.train.GradientDescentOptimizer(learning_rate)
# 优化目标:让loss最小化
update = opt.apply_gradients(opt.compute_gradients(loss))
# 模型持久化
saver = tf.train.Saver(tf.global_variables())
return encoder_inputs, decoder_inputs, target_weights,outputs, loss, update, saver, targets
#return encoder_inputs, decoder_inputs, target_weights, outputs, loss,update
def train():
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update,saver, targets= get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
sess.run(tf.global_variables_initializer())
for i in range(2000):
[loss_ret, _] = sess.run([loss, update], input_feed)
if i %100 == 0:
print( 'step=', i, 'loss=', loss_ret)
# 模型持久化
saver.save(sess, output_dir)
def predict():
"""
预测过程
"""
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver, targets= get_model(feed_previous=True)
# 从文件恢复模型
saver.restore(sess, output_dir)
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
# 预测输出
outputs = sess.run(outputs, input_feed)
# 一共试验样本有2个,所以分别遍历
for sample_index in range(2):
# 因为输出数据每一个是num_decoder_symbols维的
# 因此找到数值最大的那个就是预测的id,就是这里的argmax函数的功能
outputs_seq = [int(np.argmax(logit[sample_index], axis=0)) for logit in outputs]
# 如果是结尾符,那么后面的语句就不输出了
if EOS_ID in outputs_seq:
outputs_seq = outputs_seq[:outputs_seq.index(EOS_ID)]
outputs_seq = [str(v) for v in outputs_seq]
print(" ".join(outputs_seq))
if __name__ == "__main__":
tf.reset_default_graph()
train()
tf.reset_default_graph()
predict()
运行结果:
step= 0 loss= 2.81223
step= 100 loss= 1.31877
step= 200 loss= 0.459723
step= 300 loss= 0.144857
step= 400 loss= 0.0428859
step= 500 loss= 0.0206691
step= 600 loss= 0.0127222
step= 700 loss= 0.00889739
step= 800 loss= 0.00671659
step= 900 loss= 0.00533214
step= 1000 loss= 0.0043858
step= 1100 loss= 0.00370342
step= 1200 loss= 0.00319082
step= 1300 loss= 0.00279343
step= 1400 loss= 0.00247735
step= 1500 loss= 0.00222061
step= 1600 loss= 0.00200841
step= 1700 loss= 0.00183036
step= 1800 loss= 0.00167907
step= 1900 loss= 0.00154906
INFO:tensorflow:Restoring parameters from ./model/chatbot/demo
7 9 11
9 11 13
至此,我们算有了小小的成就了。
比较仔细的人会发现,在做预测的时候依然是按照完整的encoder_inputs和decoder_inputs计算的,那么怎么能证明模型不是直接使用了decoder_inputs来预测出的输出呢?那么我们来继续改进predict,让我们可以手工输入一串数字(只有encoder部分),看看模型能不能预测出输出
17.4.2.4优化模型
首先我们实现一个从输入空格分隔的数字id串,转成预测用的encoder、decoder、target_weight的函数。
def seq_to_encoder(input_seq):
"""从输入空格分隔的数字id串,转成预测用的encoder、decoder、target_weight等
"""
input_seq_array = [int(v) for v in input_seq.split()]
encoder_input = [PAD_ID] * (input_seq_len - len(input_seq_array)) + input_seq_array
decoder_input = [GO_ID] + [PAD_ID] * (output_seq_len - 1)
encoder_inputs = [np.array([v], dtype=np.int32) for v in encoder_input]
decoder_inputs = [np.array([v], dtype=np.int32) for v in decoder_input]
target_weights = [np.array([1.0], dtype=np.float32)] * output_seq_len
return encoder_inputs, decoder_inputs, target_weights
然后我们改写predict函数如下:
def predict():
"""
预测过程
"""
with tf.Session() as sess:
encoder_inputs, decoder_inputs, target_weights,outputs, loss, update, saver, targets=get_model(feed_previous=True)
#encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver= get_model(feed_previous=True)
saver.restore(sess, output_dir)
sys.stdout.write("> ")
#sys.stdout.flush()
#input_seq = sys.stdin.readline()
input_seq="5 7 9"
while input_seq:
input_seq = input_seq.strip()
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= seq_to_encoder(input_seq)
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
# 预测输出
outputs_seq = sess.run(outputs, input_feed)
# 因为输出数据每一个是num_decoder_symbols维的
# 因此找到数值最大的那个就是预测的id,就是这里的argmax函数的功能
outputs_seq = [int(np.argmax(logit[0], axis=0)) for logit in outputs_seq]
# 如果是结尾符,那么后面的语句就不输出了
if EOS_ID in outputs_seq:
outputs_seq = outputs_seq[:outputs_seq.index(EOS_ID)]
outputs_seq = [str(v) for v in outputs_seq]
print( " ".join(outputs_seq))
sys.stdout.write(">")
sys.stdout.flush()
input_seq = sys.stdin.readline()
#input_seq="1 3 5"
重新执行predict如下:
tf.reset_default_graph()
predict()
运行结果:
INFO:tensorflow:Restoring parameters from ./model/chatbot/demo
> 9 11 13
>
这个结果不错,输入5 7 9 预测为9 11 13。
那么我们如果输入一个新的测试样本会怎么样呢?他能不能预测出我们是在推导奇数序列呢?
当我们输入7 9 11的时候发现他报错了,原因是我们设置了num_encoder_symbols = 10,而11无法表达了,所以我们为了训练一个强大的模型,我们修改参数并增加样本,如下:
# 最大输入符号数
num_encoder_symbols = 32
# 最大输出符号数
num_decoder_symbols = 32
……
train_set = [
[[5, 7, 9], [11, 13, 15, EOS_ID]],
[[7, 9, 11], [13, 15, 17, EOS_ID]],
[[15, 17, 19], [21, 23, 25, EOS_ID]]
]
我们把迭代次数扩大到2000次
修改参数,添加函数,修改predict函数,最后综合在一起,如下:
import numpy as np
import tensorflow as tf
import os
import sys
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
output_dir='./model/chatbot/demo'
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
# 结尾标记
EOS_ID = 2
# LSTM神经元size
size = 8
# 最大输入符号数
#num_encoder_symbols = 10
num_encoder_symbols = 32
# 最大输出符号数
#num_decoder_symbols = 16
num_decoder_symbols = 32
# 学习率
learning_rate = 0.1
def seq_to_encoder(input_seq):
"""从输入空格分隔的数字id串,转成预测用的encoder、decoder、target_weight等
"""
input_seq_array = [int(v) for v in input_seq.split()]
encoder_input = [PAD_ID] * (input_seq_len - len(input_seq_array)) + input_seq_array
decoder_input = [GO_ID] + [PAD_ID] * (output_seq_len - 1)
encoder_inputs = [np.array([v], dtype=np.int32) for v in encoder_input]
decoder_inputs = [np.array([v], dtype=np.int32) for v in decoder_input]
target_weights = [np.array([1.0], dtype=np.float32)] * output_seq_len
return encoder_inputs, decoder_inputs, target_weights
def get_samples():
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32),
array([0, 0], dtype=int32),
array([1, 3], dtype=int32),
array([3, 5], dtype=int32),
array([5, 7], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32),
array([7, 9], dtype=int32),
array([ 9, 11], dtype=int32),
array([11, 13], dtype=int32),
array([0, 0], dtype=int32)]
"""
#train_set = [[[1, 3, 5], [7, 9, 11, EOS_ID]], [[3, 5, 7], [9, 11, 13, EOS_ID]]]
train_set = [[[5, 7, 9], [11, 13, 15, EOS_ID]],
[[7, 9, 11], [13, 15, 17, EOS_ID]],
[[15, 17, 19], [21, 23, 25, EOS_ID]]]
encoder_input_0 = [PAD_ID] * (input_seq_len - len(train_set[0][0]))+ train_set[0][0]
encoder_input_1 = [PAD_ID] * (input_seq_len - len(train_set[1][0]))+ train_set[1][0]
decoder_input_0 = [GO_ID] + train_set[0][1]+ [EOS_ID] * (output_seq_len - len(train_set[0][1]) - 2)
decoder_input_1 = [GO_ID] + train_set[1][1]+ [EOS_ID] * (output_seq_len - len(train_set[1][1]) - 2)
encoder_inputs = []
decoder_inputs = []
target_weights = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input_0[length_idx],
encoder_input_1[length_idx]], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input_0[length_idx],
decoder_input_1[length_idx]], dtype=np.int32))
target_weights.append(np.array([
0.0 if length_idx == output_seq_len - 1
or decoder_input_0[length_idx] == PAD_ID else 1.0,
0.0 if length_idx == output_seq_len - 1
or decoder_input_1[length_idx] == PAD_ID else 1.0,
], dtype=np.float32))
return encoder_inputs, decoder_inputs, target_weights
def get_model(feed_previous=False):
"""构造模型
"""
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None],
name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None],
name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=feed_previous,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
# 梯度下降优化器
opt = tf.train.GradientDescentOptimizer(learning_rate)
# 优化目标:让loss最小化
update = opt.apply_gradients(opt.compute_gradients(loss))
# 模型持久化
saver = tf.train.Saver(tf.global_variables())
return encoder_inputs, decoder_inputs, target_weights,outputs, loss, update, saver, targets
#return encoder_inputs, decoder_inputs, target_weights, outputs, loss,update
def train():
with tf.Session() as sess:
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= get_samples()
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update,saver, targets= get_model()
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
sess.run(tf.global_variables_initializer())
for i in range(2000):
[loss_ret, _] = sess.run([loss, update], input_feed)
if i %100 == 0:
print( 'step=', i, 'loss=', loss_ret)
# 模型持久化
saver.save(sess, output_dir)
def predict():
"""
预测过程
"""
with tf.Session() as sess:
encoder_inputs, decoder_inputs, target_weights,outputs, loss, update, saver, targets=get_model(feed_previous=True)
#encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver= get_model(feed_previous=True)
saver.restore(sess, output_dir)
sys.stdout.write("> ")
#sys.stdout.flush()
#input_seq = sys.stdin.readline()
input_seq="9 11 13"
while input_seq:
input_seq = input_seq.strip()
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= seq_to_encoder(input_seq)
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
# 预测输出
outputs_seq = sess.run(outputs, input_feed)
# 因为输出数据每一个是num_decoder_symbols维的
# 因此找到数值最大的那个就是预测的id,就是这里的argmax函数的功能
outputs_seq = [int(np.argmax(logit[0], axis=0)) for logit in outputs_seq]
# 如果是结尾符,那么后面的语句就不输出了
if EOS_ID in outputs_seq:
outputs_seq = outputs_seq[:outputs_seq.index(EOS_ID)]
outputs_seq = [str(v) for v in outputs_seq]
print( " ".join(outputs_seq))
sys.stdout.write(">")
sys.stdout.flush()
input_seq = sys.stdin.readline()
#input_seq="1 3 5"
if __name__ == "__main__":
tf.reset_default_graph()
train()
tf.reset_default_graph()
predict()
运行结果为:
step= 0 loss= 3.47917
step= 100 loss= 1.15968
step= 200 loss= 0.280037
step= 300 loss= 0.0783488
step= 400 loss= 0.0339385
step= 500 loss= 0.0198116
step= 600 loss= 0.0133718
step= 700 loss= 0.00981527
step= 800 loss= 0.00761077
step= 900 loss= 0.00613428
step= 1000 loss= 0.00508853
step= 1100 loss= 0.00431588
step= 1200 loss= 0.00372594
step= 1300 loss= 0.00326322
step= 1400 loss= 0.00289231
step= 1500 loss= 0.00258943
step= 1600 loss= 0.00233817
step= 1700 loss= 0.00212704
step= 1800 loss= 0.00194738
step= 1900 loss= 0.00179307
INFO:tensorflow:Restoring parameters from ./model/chatbot/demo
> 13 15
输入:9 11 13 预测为:13 15
说明修改参数后,可以输入大于10的数,而且预测结果为13 15 效果还不错。
17.4.3 用文本数据训练seq2seq模型
到现在,我们依然在玩的只是数字的游戏,怎么样才能和中文对话扯上关系呢?很简单,在训练时把中文词汇转成id号,在预测时,把预测到的id转成中文就可以了
1)首先我们需要对中文分词,为此创建建一个WordToken类,其中load函数负责加载样本,并生成word2id_dict和id2word_dict词典,word2id函数负责将词汇转成id,id2word负责将id转成词汇:
import sys
import jieba
class WordToken(object):
def __init__(self):
# 最小起始id号, 保留的用于表示特殊标记
self.START_ID = 4
self.word2id_dict = {}
self.id2word_dict = {}
def load_file_list(self, file_list, min_freq):
"""
加载样本文件列表,全部切词后统计词频,按词频由高到低排序后顺次编号
并存到self.word2id_dict和self.id2word_dict中
"""
words_count = {}
for file in file_list:
with open(file, 'r') as file_object:
for line in file_object.readlines():
line = line.strip()
seg_list = jieba.cut(line)
for str in seg_list:
if str in words_count:
words_count[str] = words_count[str] + 1
else:
words_count[str] = 1
sorted_list = [[v[1], v[0]] for v in words_count.items()]
sorted_list.sort(reverse=True)
for index, item in enumerate(sorted_list):
word = item[1]
if item[0] < min_freq: break self.word2id_dict[word] = self.START_ID + index self.id2word_dict[self.START_ID + index] = word return index def word2id(self, word): if not isinstance(word, unicode): print("Exception: error word not unicode") sys.exit(1) if word in self.word2id_dict: return self.word2id_dict[word] else: return None def id2word(self, id): id = int(id) if id in self.id2word_dict: return self.id2word_dict[id] else: return None 2)定义获取训练集的函数get_train_set,如下: def get_train_set(): global num_encoder_symbols, num_decoder_symbols train_set = [] with open('./data/chatbot/question.txt', 'r') as question_file: with open('./data/chatbot/answer.txt', 'r') as answer_file: while True: question = question_file.readline() answer = answer_file.readline() if question and answer: question = question.strip() answer = answer.strip() question_id_list = get_id_list_from(question) answer_id_list = get_id_list_from(answer) answer_id_list.append(EOS_ID) train_set.append([question_id_list, answer_id_list]) else: break return train_set
3)定义获取句子id的函数 get_id_list_from
def get_id_list_from(sentence): sentence_id_list = [] seg_list = jieba.cut(sentence) for str in seg_list: id = wordToken.word2id(str) if id: sentence_id_list.append(wordToken.word2id(str)) return sentence_id_list
4)导入文件,并自动获取num_encoder_symbols、num_decoder_symbols
#import word_token import jieba wordToken = WordToken() # 放在全局的位置,为了动态算出num_encoder_symbols和num_decoder_symbols max_token_id = wordToken.load_file_list(['./data/chatbot/question.txt', './data/chatbot/answer.txt'],10) num_encoder_symbols = max_token_id + 5 num_decoder_symbols = max_token_id + 5
结果显示num_encoder_symbols、num_decoder_symbols均为90 5)重新修改预测编码
def predict(): """ 预测过程 """ with tf.Session() as sess: encoder_inputs, decoder_inputs, target_weights,outputs, loss, update, saver, targets= get_model(feed_previous=True) saver.restore(sess, output_dir) sys.stdout.write("> ")
sys.stdout.flush()
input_seq = sys.stdin.readline()
while input_seq:
input_seq = input_seq.strip()
input_id_list = get_id_list_from(input_seq)
if (len(input_id_list)):
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights= seq_to_encoder(' '.join([str(v) for v in input_id_list]))
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name]= np.zeros([2], dtype=np.int32)
# 预测输出
outputs_seq = sess.run(outputs, input_feed)
# 因为输出数据每一个是num_decoder_symbols维的
# 因此找到数值最大的那个就是预测的id,就是这里的argmax函数的功能
outputs_seq = [int(np.argmax(logit[0], axis=0)) for logit in outputs_seq]
# 如果是结尾符,那么后面的语句就不输出了
if EOS_ID in outputs_seq:
outputs_seq = outputs_seq[:outputs_seq.index(EOS_ID)]
outputs_seq = [wordToken.id2word(v) for v in outputs_seq]
print( " ".join(outputs_seq))
else:
print("WARN:词汇不在服务区")
sys.stdout.write("> ")
sys.stdout.flush()
input_seq = sys.stdin.readline()
6)优化学习率参数
我们发现模型收敛的非常慢,因为我们设置的学习率是0.1,我们希望首先学习率大一些,每当下一步的loss和上一步相比反弹(反而增大)的时候我们再尝试降低学习率,方法如下,首先我们不再直接用learning_rate,而是初始化一个学习率:
然后在get_model中创建一个变量,并用init_learning_rate初始化:
learning_rate = tf.Variable(float(init_learning_rate), trainable=False, dtype=tf.float32)
之后再创建一个操作,目的是再适当的时候把学习率打9折:
learning_rate_decay_op = learning_rate.assign(learning_rate * 0.9)
7)整合后的程序
其中对学习率、优化算法等进行调整,调整后的loss循环10000次后,loss= 0.758005 。
import sys
import numpy as np
import tensorflow as tf
from tensorflow.contrib.legacy_seq2seq.python.ops import seq2seq
import jieba
import random
# 输入序列长度
input_seq_len = 5
# 输出序列长度
output_seq_len = 5
# 空值填充0
PAD_ID = 0
# 输出序列起始标记
GO_ID = 1
# 结尾标记
EOS_ID = 2
# LSTM神经元size
size = 8
# 初始学习率
init_learning_rate = 0.001
# 在样本中出现频率超过这个值才会进入词表
min_freq = 10
wordToken = WordToken()
output_dir='./model/chatbot/demo'
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# 放在全局的位置,为了动态算出num_encoder_symbols和num_decoder_symbols
max_token_id = wordToken.load_file_list(['./data/chatbot/question.txt', './data/chatbot/answer.txt'], min_freq)
num_encoder_symbols = max_token_id + 5
num_decoder_symbols = max_token_id + 5
def get_id_list_from(sentence):
sentence_id_list = []
seg_list = jieba.cut(sentence)
for str in seg_list:
id = wordToken.word2id(str)
if id:
sentence_id_list.append(wordToken.word2id(str))
return sentence_id_list
def get_train_set():
global num_encoder_symbols, num_decoder_symbols
train_set = []
with open('./data/chatbot/question.txt', 'r') as question_file:
with open('./data/chatbot/answer.txt', 'r') as answer_file:
while True:
question = question_file.readline()
answer = answer_file.readline()
if question and answer:
question = question.strip()
answer = answer.strip()
question_id_list = get_id_list_from(question)
answer_id_list = get_id_list_from(answer)
if len(question_id_list) > 0 and len(answer_id_list) > 0:
answer_id_list.append(EOS_ID)
train_set.append([question_id_list, answer_id_list])
else:
break
return train_set
def get_samples(train_set, batch_num):
"""构造样本数据
:return:
encoder_inputs: [array([0, 0], dtype=int32), array([0, 0], dtype=int32), array([5, 5], dtype=int32),
array([7, 7], dtype=int32), array([9, 9], dtype=int32)]
decoder_inputs: [array([1, 1], dtype=int32), array([11, 11], dtype=int32), array([13, 13], dtype=int32),
array([15, 15], dtype=int32), array([2, 2], dtype=int32)]
"""
# train_set = [[[5, 7, 9], [11, 13, 15, EOS_ID]], [[7, 9, 11], [13, 15, 17, EOS_ID]], [[15, 17, 19], [21, 23, 25, EOS_ID]]]
raw_encoder_input = []
raw_decoder_input = []
if batch_num >= len(train_set):
batch_train_set = train_set
else:
random_start = random.randint(0, len(train_set)-batch_num)
batch_train_set = train_set[random_start:random_start+batch_num]
for sample in batch_train_set:
raw_encoder_input.append([PAD_ID] * (input_seq_len - len(sample[0])) + sample[0])
raw_decoder_input.append([GO_ID] + sample[1] + [PAD_ID] * (output_seq_len - len(sample[1]) - 1))
encoder_inputs = []
decoder_inputs = []
target_weights = []
for length_idx in range(input_seq_len):
encoder_inputs.append(np.array([encoder_input[length_idx] for encoder_input in raw_encoder_input], dtype=np.int32))
for length_idx in range(output_seq_len):
decoder_inputs.append(np.array([decoder_input[length_idx] for decoder_input in raw_decoder_input], dtype=np.int32))
target_weights.append(np.array([
0.0 if length_idx == output_seq_len - 1 or decoder_input[length_idx] == PAD_ID else 1.0 for decoder_input in raw_decoder_input
], dtype=np.float32))
return encoder_inputs, decoder_inputs, target_weights
def seq_to_encoder(input_seq):
"""从输入空格分隔的数字id串,转成预测用的encoder、decoder、target_weight等
"""
input_seq_array = [int(v) for v in input_seq.split()]
encoder_input = [PAD_ID] * (input_seq_len - len(input_seq_array)) + input_seq_array
decoder_input = [GO_ID] + [PAD_ID] * (output_seq_len - 1)
encoder_inputs = [np.array([v], dtype=np.int32) for v in encoder_input]
decoder_inputs = [np.array([v], dtype=np.int32) for v in decoder_input]
target_weights = [np.array([1.0], dtype=np.float32)] * output_seq_len
return encoder_inputs, decoder_inputs, target_weights
def get_model(feed_previous=False):
"""构造模型
"""
learning_rate = tf.Variable(float(init_learning_rate), trainable=False, dtype=tf.float32)
learning_rate_decay_op = learning_rate.assign(learning_rate * 0.9)
encoder_inputs = []
decoder_inputs = []
target_weights = []
for i in range(input_seq_len):
encoder_inputs.append(tf.placeholder(tf.int32, shape=[None], name="encoder{0}".format(i)))
for i in range(output_seq_len + 1):
decoder_inputs.append(tf.placeholder(tf.int32, shape=[None], name="decoder{0}".format(i)))
for i in range(output_seq_len):
target_weights.append(tf.placeholder(tf.float32, shape=[None], name="weight{0}".format(i)))
# decoder_inputs左移一个时序作为targets
targets = [decoder_inputs[i + 1] for i in range(output_seq_len)]
cell = tf.contrib.rnn.BasicLSTMCell(size)
# 这里输出的状态我们不需要
outputs, _ = seq2seq.embedding_attention_seq2seq(
encoder_inputs,
decoder_inputs[:output_seq_len],
cell,
num_encoder_symbols=num_encoder_symbols,
num_decoder_symbols=num_decoder_symbols,
embedding_size=size,
output_projection=None,
feed_previous=feed_previous,
dtype=tf.float32)
# 计算加权交叉熵损失
loss = seq2seq.sequence_loss(outputs, targets, target_weights)
# 梯度下降优化器
#opt = tf.train.GradientDescentOptimizer(learning_rate)
opt = tf.train.AdamOptimizer(learning_rate=learning_rate)
# 优化目标:让loss最小化
update = opt.apply_gradients(opt.compute_gradients(loss))
# 模型持久化
saver = tf.train.Saver(tf.global_variables())
return encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver, learning_rate_decay_op, learning_rate
def train():
"""
训练过程
"""
# train_set = [[[5, 7, 9], [11, 13, 15, EOS_ID]], [[7, 9, 11], [13, 15, 17, EOS_ID]],
# [[15, 17, 19], [21, 23, 25, EOS_ID]]]
train_set = get_train_set()
with tf.Session() as sess:
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver, learning_rate_decay_op, learning_rate = get_model()
# 全部变量初始化
sess.run(tf.global_variables_initializer())
# 训练很多次迭代,每隔10次打印一次loss,可以看情况直接ctrl+c停止
previous_losses = []
for step in range(10000):
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights = get_samples(train_set, 1000)
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([len(sample_decoder_inputs[0])], dtype=np.int32)
[loss_ret, _] = sess.run([loss, update], input_feed)
if step % 100 == 0:
print( 'step=', step, 'loss=', loss_ret, 'learning_rate=', learning_rate.eval())
if len(previous_losses) > 5 and loss_ret > max(previous_losses[-5:]):
sess.run(learning_rate_decay_op)
previous_losses.append(loss_ret)
# 模型持久化
saver.save(sess, output_dir)
def predict():
"""
预测过程
"""
with tf.Session() as sess:
encoder_inputs, decoder_inputs, target_weights, outputs, loss, update, saver, learning_rate_decay_op, learning_rate = get_model(feed_previous=True)
saver.restore(sess, output_dir)
sys.stdout.write("> ")
sys.stdout.flush()
#input_seq = sys.stdin.readline()
input_seq=input()
while input_seq:
input_seq = input_seq.strip()
input_id_list = get_id_list_from(input_seq)
if (len(input_id_list)):
sample_encoder_inputs, sample_decoder_inputs, sample_target_weights = seq_to_encoder(' '.join([str(v) for v in input_id_list]))
input_feed = {}
for l in range(input_seq_len):
input_feed[encoder_inputs[l].name] = sample_encoder_inputs[l]
for l in range(output_seq_len):
input_feed[decoder_inputs[l].name] = sample_decoder_inputs[l]
input_feed[target_weights[l].name] = sample_target_weights[l]
input_feed[decoder_inputs[output_seq_len].name] = np.zeros([2], dtype=np.int32)
# 预测输出
outputs_seq = sess.run(outputs, input_feed)
# 因为输出数据每一个是num_decoder_symbols维的,因此找到数值最大的那个就是预测的id,就是这里的argmax函数的功能
outputs_seq = [int(np.argmax(logit[0], axis=0)) for logit in outputs_seq]
# 如果是结尾符,那么后面的语句就不输出了
if EOS_ID in outputs_seq:
outputs_seq = outputs_seq[:outputs_seq.index(EOS_ID)]
outputs_seq = [wordToken.id2word(v) for v in outputs_seq]
print(" ".join(outputs_seq))
else:
print("WARN:词汇不在服务区")
sys.stdout.write("> ")
sys.stdout.flush()
input_seq = input()
if __name__ == "__main__":
tf.reset_default_graph()
train()
tf.reset_default_graph()
predict()
迭代次数、loss与学习率间的运行结果如下:
step= 0 loss= 4.48504 learning_rate= 0.001
step= 100 loss= 3.33924 learning_rate= 0.001
step= 200 loss= 2.90026 learning_rate= 0.001
step= 300 loss= 2.65296 learning_rate= 0.001
step= 400 loss= 2.48741 learning_rate= 0.001
step= 500 loss= 2.32334 learning_rate= 0.001
.............................................
step= 9000 loss= 0.765676 learning_rate= 0.000729
step= 9100 loss= 0.758894 learning_rate= 0.000729
step= 9200 loss= 0.75713 learning_rate= 0.000729
step= 9300 loss= 0.758076 learning_rate= 0.000729
step= 9400 loss= 0.752497 learning_rate= 0.000729
step= 9500 loss= 0.770046 learning_rate= 0.000729
step= 9600 loss= 0.749504 learning_rate= 0.0006561
step= 9700 loss= 0.747211 learning_rate= 0.0006561
step= 9800 loss= 0.747742 learning_rate= 0.0006561
step= 9900 loss= 0.758005 learning_rate= 0.0006561
测试部分结果如下:
> 你说
我 想 你
> 哈哈
什么
> 爱你
= 。 =
> 你吃了吗
吃 了
> 喜欢你
我 喜欢 !
> 工作
WARN:词汇不在服务区
> 去上海
你 啊 !
> 再见
WARN:词汇不在服务区
>
17.4.4 小结
本文从理论到实践讲解了怎么一步一步实现一个自动聊天机器人模型,并基于1000条样本,用了20分钟左右训练了一个聊天模型,试验效果比较好,核心逻辑是调用了tensorflow的embedding_attention_seq2seq,也就是带注意力的seq2seq模型,其中神经网络单元是LSTM。
由于语料有限,设备有限,只验证了小规模样本,如果大家想做一个更好的聊天系统,可以下载更多对话内容。
参考:
http://blog.csdn.net/malefactor/article/details/50550211
http://www.shareditor.com/blogshow?blogId=136【内含数据文件、及代码等】
https://www.geekhub.cn/a/2214.html
How Does Attention Work in Encoder-Decoder Recurrent Neural Networks
How to Develop an Encoder-Decoder Model with Attention in Keras










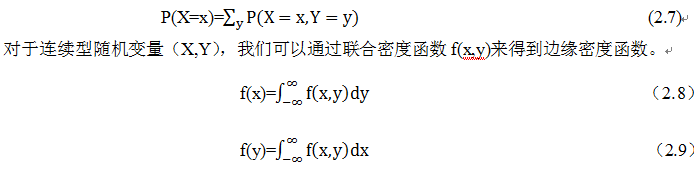








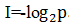 。为此,可能有不少人会问,为何用对数,前面还要带上负号?
。为此,可能有不少人会问,为何用对数,前面还要带上负号?

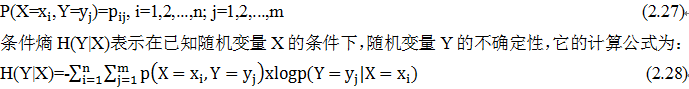





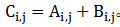 。矩阵也可以和向量相加,只要它们的列数相同,相加的结果是矩阵每行与向量相加,这种隐式地复制向量b到很多位置的方式称为广播(broadcasting),以下我们通过一个代码示例来说明。
。矩阵也可以和向量相加,只要它们的列数相同,相加的结果是矩阵每行与向量相加,这种隐式地复制向量b到很多位置的方式称为广播(broadcasting),以下我们通过一个代码示例来说明。


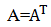 成立, 则称方阵A为对称矩阵。
成立, 则称方阵A为对称矩阵。





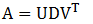 (1.15)
(1.15)











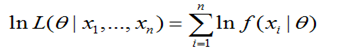


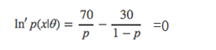
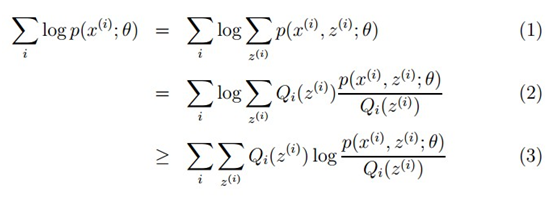
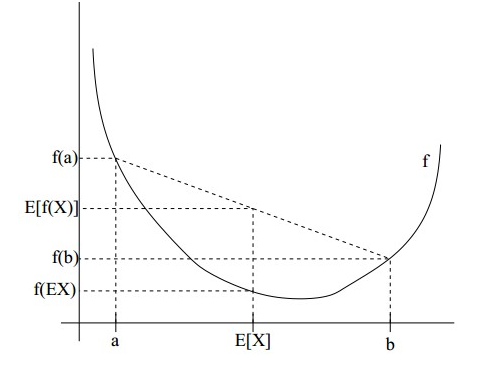
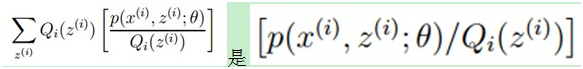
 ,所以就可以得到公式(3)的不等式了。
,所以就可以得到公式(3)的不等式了。 4.6.2.7代码实现
4.6.2.7代码实现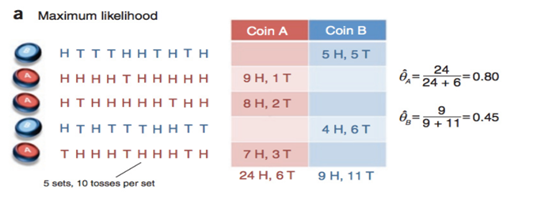


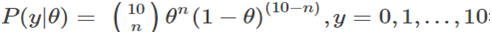









 每个
每个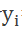 都依次这么产生,那么看起来就是整个系统根据输入句子X生成了目标句子Y。
都依次这么产生,那么看起来就是整个系统根据输入句子X生成了目标句子Y。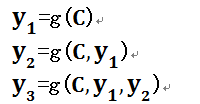


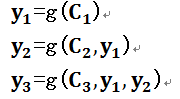

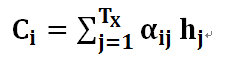


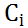 的生成过程
的生成过程