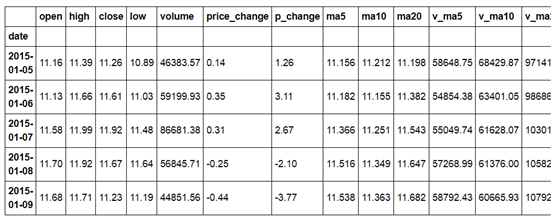
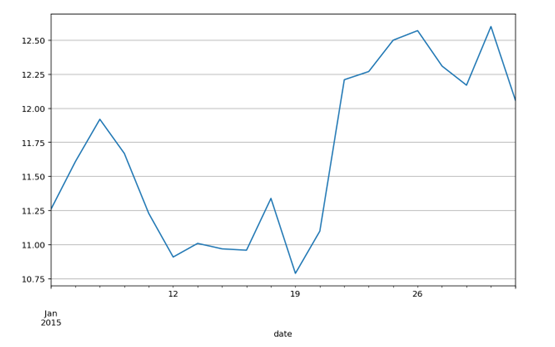
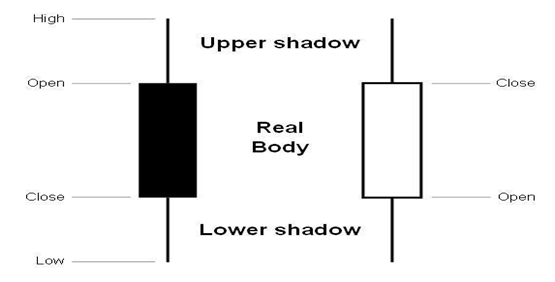
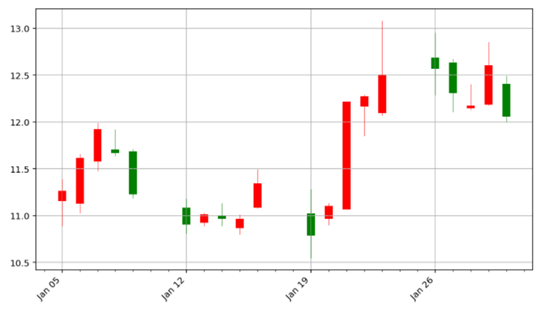
第1章 MySQL简介
1.1 数据库泛述
为什么要学习数据库?
这个问题我觉得还是从反面来回答比较好,数据库出故障了,会发生啥呢?
学数据库与我找工作或找到更好工作有关系吗?有,关系还很大哦。当然,如果你去应聘不用电脑的职业除外。否则,很可能产生“一丑遮百俊”。
学了数据库有哪些好处?
其他好处不好说,但如果你学了熟悉数据库,对学习其他技术有非常大得帮助,尤其对学习大数据相关技术如Hive、HBase、SparkSQL、SparkRDD等等更是如此,数据库很多都是相通或相似的,学好一个学其他的就轻松多了。
有哪些数据库?
数据库种类很多,从大得方面来说,可分为关系型数据库和非关系型数据库,如MySQL、SQL Server、Oracle、DB2、Sybase等属于关系型数据库,近些年比较火的HBase、MongoDB、Redis等属于非关系型数据库,从存储方式方面来说,可分为行存储数据库、列存储数据库、键值数据库、NoSQL数据库等,当然各类关系型数据库或非关系型数据库自身都各有一些特点。这里就不展开说了。
如何学习数据库?
这个问题有点仁者见仁智者见智,一百人可能有一百个答案,不过我个人认为,数据库作为一个基础性非常强、使用非常广泛的系统,多花些时间进行一些有系统的学习是非常必要,好的基础将大大提升你的竞争力、拓展你的职业发展空间。
1.2 MySQL特点
为何选择MySQL? 它有哪些特点?
MySQL是由原MySQL AB公司自主研发的,现在已经被Sun公司收购,是目前IT行业最流行的开放源代码的数据库管理系统,同时它也是一个支持多线程高并发多用户的关系型数据库管理系统。支持Linux、Windows、MAC等多种操作系统,虽然功能上没有其他的大型数据库Oracle、DB2等那么齐全,但好用、易用、开源、可靠性等特点受到成千上万企业和用户的青睐重要原因。
向大家推荐几个学习MySQL的网站:
MySQL社区: http://www.mysqlpub.com/
MySQL菜鸟教程: http://www.runoob.com/mysql/mysql-tutorial.html
MySQL官网: http://www.mysql.com/
《深入浅出MySQL》唐汉名等著
1.3 数据库基础
数据库是一个长期存储在计算机内的、有组织、共享、统一的数据集合。作为关系型数据其关系可理解为数据库表,表是一系列二维数组的集合。
表定义:表(Table),在关系型数据库中,表是一系列二维数组的集合,由纵向的列和横向的行组成,列又称为字段,行又称为记录。
表样例:stud_info(学生基本信息表)
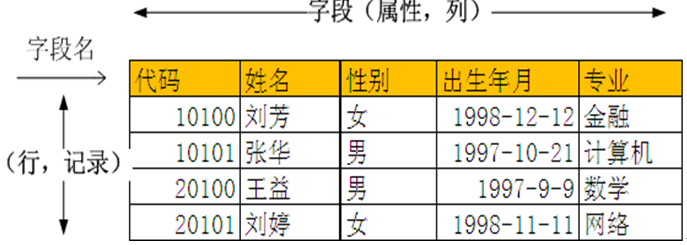
表要素有:
关系或表、列,字段行,记录
数据类型:
字符串数据类型、整数型、日期/时间类型、浮点数据型等
关键字,主键:
主键(Primary key),唯一标志表的每一条记录,可以定义表中一列或多列为主键, 主键列上不能有重复的值,也不能为空,如stud_info表中代码字段为该表的主键。
关系模式或表结构,格式为:表名称(属性1,属性2,…属性n)
1.4 数据库语言
我们一般通过数据库语言与数据库打交道,其中SQL是我们常用的,SQL的含义是结构化查询语言(Structured Query Language)。
SQL语言分类
数据定义语言(DDL)
如:DROP,CREATE,ALTER等
数据操作语言(DML)
如:INSERT,UPDATE,DELETE等
数据查询语言(DQL)
SELECT等
数据控制语言(DCL)
GRANT,REVOKE,COMMIT,ROLLBAK等。
为进一步理解SQL语句含义,下面以创建一张表的SQL语句为例,表名为t_student,具体SQL语句如下:
CREATE TABLE t_student
(
stud_id INT NOT NULL,
stud_name VARCHAR(40) NOT NULL,
stud_sex CHAR(1),
stud_birthday DATE,
PRIMARY KEY (stud_id)
);
这是一个典型的数据定义语言(DDL),该表共有4个字段,分别为stud_id,stud_name,stud_sex,stud_birthday,其中stud_id为主键。
目前这个表是空表,只有结构没有数据,我们可以用数据操作语句(DML)往表插入记录或数据。
INSERT INTO t_student(stud_id,stud_name,stud_sex,stud_birthday)
VALUES(1001001,'刘芳','F','1995-06-19');
以上记录是否成功插入到表中呢?我们可以通过数据查询语言(DQL)来验证一下:
select * from t_student;
+---------+-----------+----------+---------------+
| stud_id | stud_name | stud_sex | stud_birthday |
+---------+-----------+----------+---------------+
| 1001001 | 刘芳 | F | 1995-06-19
1.5 数据库系统架构
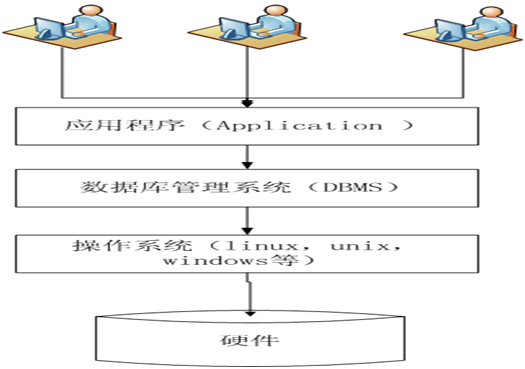
(图1-1 数据库系统架构)
第2章 安装与配置
2.1 Windows平台下安装配置
MySQL支持多平台,如常见的windows,linux等,这里我们以Windows下安装为主,然后简单说明在Linux平台上的安装。
这里介绍一个针对初学者的Windows版的MySQL安装程序(mysqlSetup.exe,文件下载链接:http://pan.baidu.com/s/1kVHK3eZ),文件大小为35M左右,版本为V5.0,依赖较少,安装方便,但基础功能都有。
以下为详细的安装步骤:
第1步:点击“mysqlSetup.exe”文件,弹出如下界面
第2步:选择安装类型,选择typical(典型安装)。

第3步:是否注册,选择skip sign-up(不注册)
第4步:开始配置服务器
第5步:在配置类型界面中,选择Detailed configuration(详细配置)

第6步:在服务器类型中,作为初学者,可以选择Developer Machine(作为开发机),占用系统资源较少,但基本功能都有。
第7步:字符集选择界面,第一个为西文编码,第二个是多字节的通用utf8编码,都不是我们通用的编码,这里选择第三个,然后在Character Set那里选择或填入“gbk”,当然也可以用“gb2312”,区别就是gbk的字库容量大,包括了gb2312的所有汉字。
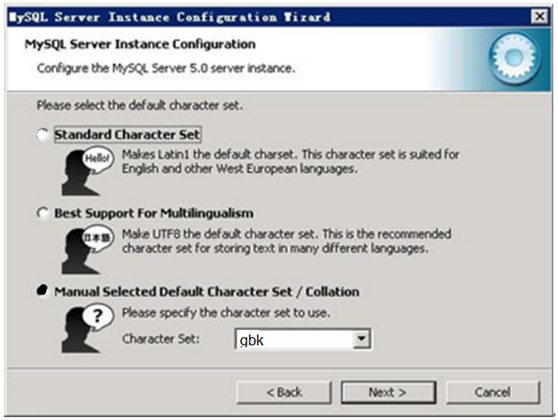
第8步:在数据库用途界面,选择Mutifunctional Database(多功能数据库)。
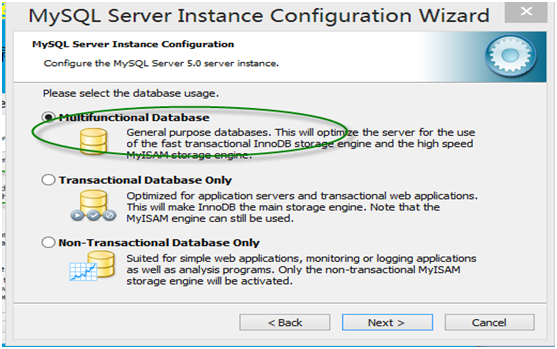
第9步:进入服务器最多并发连接数界面,作为初学者,不涉及很复杂的业务逻辑,而且并发数也需要很多,可选择第一项OLAP或OLTP,并发连接数(concurrent connection)缺省为15,当然你也可以根据需要进行修改。

第10步:配置网络,使用缺省配置即可。

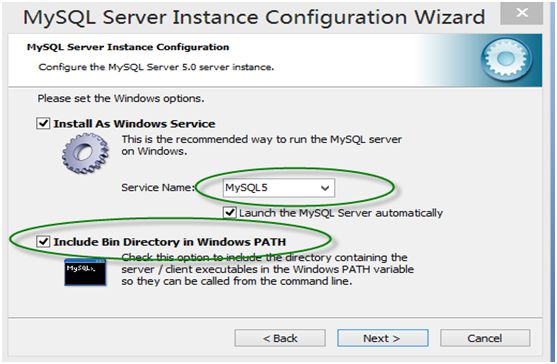
第11步:在Windows设置界面,记得在勾上“Inclode bin Directory in windows PATH”,这样自动把mysql命令所在目录放在Windows的环境变量Path中,接下来你便可在任何目录下启动mysql。
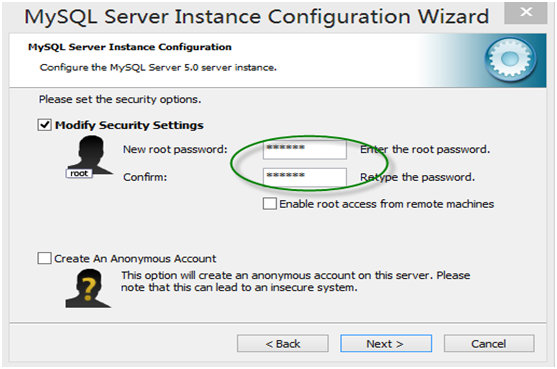
第12步,确认root用户密码
第13步,显示将执行的内容(无需选择),点击“Execute”
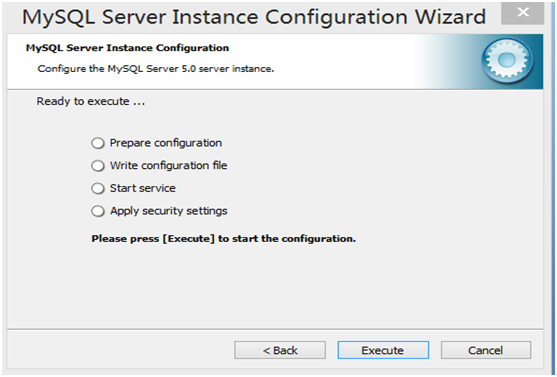
第14步 安装结束
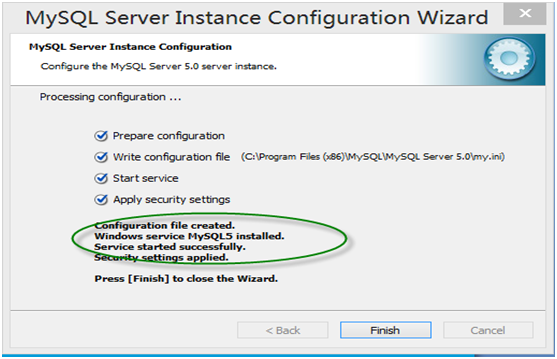
第15步 登录MyQL系统。
通过Windows命令行登录
第1步,从开始菜单选择“运行”,打开运行对话框,输入‘cmd’
第2步,按确定,打开DOS窗口。
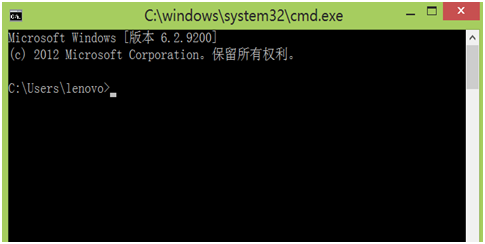
第3步,在DOS窗口中,可以通过输入命令登录MySQL系统,命令格式为:
mysql -h hostname -u username -p
其中mysql为登录命令,
-h 后的参数为服务器名称或IP地址,如果为本地服务器,可为localhost 或127.0.0.1, -u后的参数为用户名称,还没有创建其他用户时,只有root用户。
-p 后的参数为用户密码。
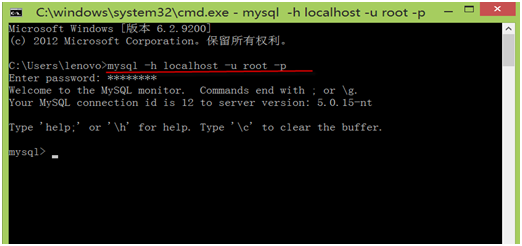
第4步,退出mysql系统,只要在mysql>后,输入quit 然后回车即可。
通过MySQL命令行登录
选择“开始”菜单,点击含“MySQL Command Line Client”字样的图标,进入登录界面,然后输入root用户密码即可登录。
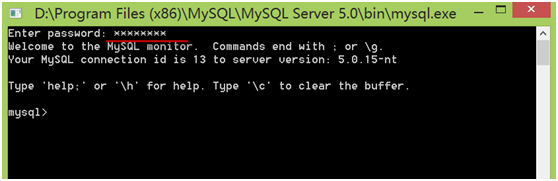
这是在登录windows下MySQL系统的几种方式,下章我们将介绍如何登录远程服务器上的MySQL系统。
第3章 操作数据库
3.1 登录Linux服务器的MySQL
在第2章我们介绍了如何在Windows下安装和配置MySQL、通过“运行”或MySQL的命令行等界面登录Windows下的MySQL系统。
如果要连接Linux下的MySQL系统,该如何配置或操作呢?这个比较简单,首先,先通过Xshell或Putty等客户端连接Linux服务器,然后在Linux命令行输入连接MySQL的信息即可。如何连接Linux系统请参考第1章的1.6节。现在我们以用户feigu(密码也是feigu)连接MySQL。

3.2 创建数据库
登录MySQL系统后,我们可查看已创建的数据库,当然,我们也可自己创建数据。MySQL中命令一般以分号(;)或\g结束。
mysql> show databases; ###查看已有数据库
+--------------------+
| Database |
+--------------------+
| information_schema | ###系统自建数据库
| mysql | ###系统自建数据库
| performance_schema | ###系统自建数据库
| testdb |
+--------------------+
4 rows in set (0.00 sec)
其中information_schema、mysql、performance_schema为系统自建数据库,用户不宜修改这些库。
创建数据库,其语法格式为:
CREATE DATABASE database_name;
创建一个数据库test_db,然后,验证创建是否成功。
mysql> CREATE DATABASE test_db; ###创建数据库test_db
Query OK, 1 row affected (0.00 sec)
mysql> show databases;
+--------------------+
| Database |
+--------------------+
| information_schema |
| mysql |
| performance_schema |
| test_db | ###创建数据库成功
| testdb |
+--------------------+
3.3 删除数据库
创建了数据库,如果不用时,我们可以删除,当然测试关系不大,平时删除数据库要非常谨慎,如果有实际数据建议先备份,然后再删除,有备无患哦。
删除数据库的命令格式为:
DROP DATABASE dabase_name;
mysql> drop database test_db; ###删除数据库test_db
Query OK, 0 rows affected (0.09 sec)
mysql> show databases;
+--------------------+
| Database |
+--------------------+
| information_schema |
| mysql |
| performance_schema |
| testdb |
+--------------------+
3.4 获取帮助信息
MySQL有很多命令,各种命令的格式一般不同,忘记一些命令的使用方法是大概率事件,万一忘记了咋办?百度、google当然不失为方法之一,实际上MySQL自身就带有很强大的帮助功能,如查看MySQL一般可用help,如果要查询具体某个命令的使用方法,用help 命令名称,非常方便而且详细。
mysql> help; ###查看帮助信息
For information about MySQL products and services, visit:
http://www.mysql.com/
For developer information, including the MySQL Reference Manual, visit:
http://dev.mysql.com/
To buy MySQL Enterprise support, training, or other products, visit:
https://shop.mysql.com/
List of all MySQL commands:
Note that all text commands must be first on line and end with ';'
? (\?) Synonym for <code>help'.
clear (\c) Clear the current input statement.
connect (\r) Reconnect to the server. Optional arguments are db and host.
delimiter (\d) Set statement delimiter.
edit (\e) Edit command with $EDITOR.
ego (\G) Send command to mysql server, display result vertically.
exit (\q) Exit mysql. Same as quit.
go (\g) Send command to mysql server.
help (\h) Display this help.
nopager (\n) Disable pager, print to stdout.
notee (\t) Don't write into outfile.
pager (\P) Set PAGER [to_pager]. Print the query results via PAGER.
print (\p) Print current command.
prompt (\R) Change your mysql prompt.
quit (\q) Quit mysql.
rehash (\#) Rebuild completion hash.
source (\.) Execute an SQL script file. Takes a file name as an argument.
status (\s) Get status information from the server.
system (\!) Execute a system shell command.
tee (\T) Set outfile [to_outfile]. Append everything into given outfile.
use (\u) Use another database. Takes database name as argument.
charset (\C) Switch to another charset. Might be needed for processing binlog with multi-byte charsets.
warnings (\W) Show warnings after every statement.
nowarning (\w) Don't show warnings after every statement.
For server side help, type 'help contents'
如何查看具体命令的使用方法?可用help 命令关键字,或? 命令关键字。如查看create database的具体使用方法。
mysql> help create dabase;
Nothing found
Please try to run 'help contents' for a list of all accessible topics
mysql> help create database;
Name: 'CREATE DATABASE'
Description:
Syntax:
CREATE {DATABASE | SCHEMA} [IF NOT EXISTS] db_name
[create_specification] ...
create_specification:
[DEFAULT] CHARACTER SET [=] charset_name
| [DEFAULT] COLLATE [=] collation_name
CREATE DATABASE creates a database with the given name. To use this
statement, you need the CREATE privilege for the database. CREATE
SCHEMA is a synonym for CREATE DATABASE.
URL: http://dev.mysql.com/doc/refman/5.5/en/create-database.html
3.5 数据库存储引擎
MySQL有个独特、强大而灵活的功能,可以根据表的用途选择存储引擎。
它提供了很多种类型的存储引擎,我们可以根据对数据处理的需求,选择不同的存储引擎,从而最大限度的利用MySQL强大的功能。MySQL支持的存储引擎有:InnoDB、MyISAM、Memory、Merge、Archive等,可以使用SHOW ENGINES语句查看目前系统支持的存储引擎的类型:
mysql> SHOW ENGINES \G
*************************** 1. row ***************************
Engine: MyISAM
Support: YES
Comment: MyISAM storage engine
Transactions: NO
XA: NO
Savepoints: NO
*************************** 2. row ***************************
Engine: MRG_MYISAM
Support: YES
Comment: Collection of identical MyISAM tables
Transactions: NO
XA: NO
Savepoints: NO
*************************** 3. row ***************************
Engine: CSV
Support: YES
Comment: CSV storage engine
Transactions: NO
XA: NO
Savepoints: NO
*************************** 4. row ***************************
Engine: BLACKHOLE
Support: YES
Comment: /dev/null storage engine (anything you write to it disappears)
Transactions: NO
XA: NO
Savepoints: NO
*************************** 5. row ***************************
Engine: MEMORY
Support: YES
Comment: Hash based, stored in memory, useful for temporary tables
Transactions: NO
XA: NO
Savepoints: NO
*************************** 6. row ***************************
Engine: FEDERATED
Support: NO
Comment: Federated MySQL storage engine
Transactions: NULL
XA: NULL
Savepoints: NULL
*************************** 7. row ***************************
Engine: ARCHIVE
Support: YES
Comment: Archive storage engine
Transactions: NO
XA: NO
Savepoints: NO
*************************** 8. row ***************************
Engine: InnoDB
Support: DEFAULT
Comment: Supports transactions, row-level locking, and foreign keys
Transactions: YES
XA: YES
Savepoints: YES
*************************** 9. row ***************************
Engine: PERFORMANCE_SCHEMA
Support: YES
Comment: Performance Schema
Transactions: NO
XA: NO
Savepoints: NO
9 rows in set (0.00 sec)
以下我们列举几种常用存储引擎。
InnoDB
InnoDB是一个健壮的事务型存储引擎,这种存储引擎已经被很多互联网公司使用,为用户操作非常大的数据存储提供了一个强大的解决方案。作为默认的存储引擎,InnoDB还引入了行级锁定和外键约束,在以下场合下,使用InnoDB是最理想的选择:
1.更新密集的表。InnoDB存储引擎特别适合处理多重并发的更新请求。
2.事务。InnoDB存储引擎是支持事务的标准MySQL存储引擎。
3.自动灾难恢复。与其它存储引擎不同,InnoDB表能够自动从灾难中恢复。
4.外键约束。MySQL支持外键的存储引擎只有InnoDB。
5.支持自动增加列AUTO_INCREMENT属性。
一般来说,如果需要事务支持,并且有较高的并发读取频率,InnoDB是不错的选择。
MyISAM
MyISAM表是独立于操作系统的,这说明可以轻松地将其从Windows服务器移植到Linux服务器;每当我们建立一个MyISAM引擎的表时,就会在本地磁盘上建立三个文件,文件名就是表明。例如,我建立了一个MyISAM引擎的tb_Demo表,那么就会生成以下三个文件:
1.tb_demo.frm,存储表定义;
2.tb_demo.MYD,存储数据;
3.tb_demo.MYI,存储索引。
MyISAM表无法处理事务,这就意味着有事务处理需求的表,不能使用MyISAM存储引擎。MyISAM存储引擎特别适合在以下几种情况下使用:
1.查询密集型的表。MyISAM存储引擎在筛选大量数据时非常迅速,这是它最突出的优点。
2.插入密集型的表。MyISAM的并发插入特性允许同时选择和插入数据。例如:MyISAM存储引擎很适合管理邮件或Web服务器日志数据等。
MEMORY
使用MySQL Memory存储引擎的出发点是速度。为得到最快的响应时间,采用的逻辑存储介质是系统内存。虽然在内存中存储表数据确实会提供很高的性能,但当mysqld守护进程崩溃时,所有的Memory数据都会丢失。获得速度的同时也带来了一些缺陷。它要求存储在Memory数据表里的数据使用的是长度不变的格式,这意味着不能使用BLOB和TEXT这样的长度可变的数据类型,VARCHAR是一种长度可变的类型,但因为它在MySQL内部当做长度固定不变的CHAR类型,所以可以使用。
一般在以下几种情况下使用Memory存储引擎:
1.目标数据较小,而且被非常频繁地访问。在内存中存放数据,所以会造成内存的使用,可以通过参数max_heap_table_size控制Memory表的大小,设置此参数,就可以限制Memory表的最大大小。
2.如果数据是临时的,而且要求必须立即可用,那么就可以存放在内存表中。
3.存储在Memory表中的数据如果突然丢失,不会对应用服务产生实质的负面影响。
Memory同时支持散列索引和B树索引。B树索引的优于散列索引的是,可以使用部分查询和通配查询,也可以使用<、>和>=等操作符方便数据挖掘。散列索引进行“相等比较”非常快,但是对“范围比较”的速度就慢多了,因此散列索引值适合使用在=和<>的操作符中,不适合在<或>操作符中,也同样不适合用在order by子句中。
表存储引擎可以在创建表时利用USING子句指定。
第4章 操作表
在关系型数据库中,表是是数据库中最重要、最基本的操作对象,是数据存储的基本单位,数据是按行存储的(非关系型数据库有些是按列存储的),同时通过表中的主键、外键、索引、非空等约束来保证数据的一致性和完整性。这一章主要介绍数据表的基本操作:如何创建表、查看表的结构、修改数据表、删除数据表等。
创建表的方式,可以命令行的方式,也可以通过客户端(navicat for mysql)或通过该客户端的建模方式创建,然后,把模型同步到数据库即可。
4.1 创建表
创建表的过程就是确定数据列的属性、制定数据完整性、一致性等约束的过程。而这些约束主要通过主键、外键、是否可空、索引等约束来实现的。
创建表的语法形式:
CREATE TABLE 表名称
(
字段名称1 数据类型 [列级的约束] [默认值],
字段名称2 数据类型 [列级的约束] [默认值],
--------
[表级的约束]
);
注:
(1)、表的名称不区分大小写,不能以SQL中的一些关键字为表名,如CREATE、ALTER、INSERT等;
(2)、列名间用逗号隔开。
下面以创建一个学生的基本信息表为例,说明如何创建一张表。
表的定义或结构如下:
学生信息(t_stud_info)表结构
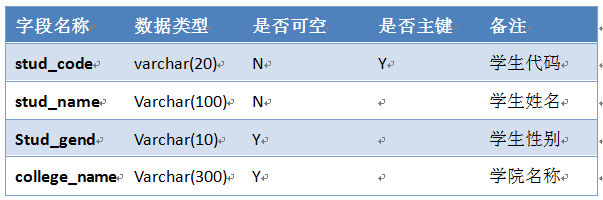
注:
(1)、stud_code这个字段为主键,作为主键(PRIMARY KEY)的字段不能为空,为空的字段不能为主键,主键可以建的一个字段上,也可建的两个或两个以上的字段上,称为组合主键;
(2)、非空字段,是指这些字段的值,不能为空(即为null)。
创建表的SQL语句:
CREATE TABLE t_stud_info
(
stud_code varchar(20) NOT NULL,
stud_name varchar(100) NOT NULL,
stud_gend varchar(10) , #没有说明NULL,说明是NULL
college_name varchar(300) NULL,
PRIMARY KEY (stud_code) #指明构成主键的字段
); #最后是分号
创建表的SQL以写好,如何执行,如何查看表结构?通过实例来说明:
直接把创建表的SQL语句放在mysql命令行执行:
mysql> use testdb; ###把表创建在该数据库上
Reading table information for completion of table and column names
You can turn off this feature to get a quicker startup with -A
Database changed
mysql> CREATE TABLE t_stud_info
-> (
-> stud_code varchar(20) NOT NULL,
-> stud_name varchar(100) NOT NULL,
-> stud_gend varchar(10) ,
-> college_name varchar(300) NULL,
-> PRIMARY KEY (stud_code)
-> );
Query OK, 0 rows affected (0.31 sec)
mysql> show tables; ###查看已创建的表
+------------------+
| Tables_in_testdb |
+------------------+
| stud_info |
| stud_info_copy |
| stud_score |
| stud_score_view |
| t_stud_info | ###表创建成功
+------------------+
5 rows in set (0.00 sec)
mysql> desc t_stud_info; ###查看表结构
+--------------+--------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+--------------+--------------+------+-----+---------+-------+
| stud_code | varchar(20) | NO | PRI | NULL | |
| stud_name | varchar(100) | NO | | NULL | |
| stud_gend | varchar(10) | YES | | NULL | |
| college_name | varchar(300) | YES | | NULL | |
+--------------+--------------+------+-----+---------+-------+
4 rows in set (0.17 sec)
mysql> show create table t_stud_info \G ###查看表的详细信息
*************************** 1. row ***************************
Table: t_stud_info
Create Table: CREATE TABLE </code>t_stud_info<code> (
</code>stud_code<code> varchar(20) NOT NULL,
</code>stud_name<code> varchar(100) NOT NULL,
</code>stud_gend<code> varchar(10) DEFAULT NULL,
</code>college_name<code> varchar(300) DEFAULT NULL,
PRIMARY KEY (</code>stud_code<code>)
) ENGINE=InnoDB DEFAULT CHARSET=utf8 ###表的存储引擎、字符集。
通过执行脚本创建表
如果一次要创建几十张表,把创建表的语句直接放在mysql命令行运行就不方便了,此时我们可以把创建这些表的SQL语句保存本地当前目录下,名为t_stud_info.sql的文件中,,具体内容请参看以下system cat t_stud_info.sql部分,然后用source命令在mysql命令下执行这个文件即可。这个source命令有点像shell命令。
mysql> system cat t_stud_info.sql; ###查看sql文件内容
DROP TABLE IF EXISTS t_stud_info;
CREATE TABLE t_stud_info
(
stud_code varchar(20) NOT NULL,
stud_name varchar(100) NOT NULL,
stud_gend varchar(10) ,
college_name varchar(300) NULL,
PRIMARY KEY (stud_code)
);
mysql> source t_stud_info.sql;
Query OK, 0 rows affected (0.03 sec)
mysql> show tables;
+------------------+
| Tables_in_testdb |
+------------------+
| stud_info |
| stud_score |
| t_stud_info | ###表创建成功
+------------------+
除了以上两种方法外,还有其他方法,如通过客户端创建、通过模型来创建等等,这里就不展开来说了。
4.2 修改表结构
表创建好以后,有时间我们可能根据新的需求,需要修改字段类型、字段名称、添加字段、新建其它约束如索引、是否可空等。当表中无数据时做这些修改比较方便,如果表已有数据可能就需要慎重,否则可能导致修改失败,此时建议备份原表数据,然后清空数据,再做修改,修改后根据新的规则把数据导入新表中。但添加字段、放大自动长度等与是否有数据无关。
4.2.1 修改字段类型
如果发现创建的表的某个字段长度太小,需要放大其长度,该如何修改呢?我们可以使用ALTER TABLE 语句来修改。
【注意】如果是正式环境的数据,记得先备份,后修改,有备无患。
修改表字段类型的语法格式:
ALTER TABLE <表名> MODIFY <字段名> <字符类型>;
我们创建一张表test01 (a1 varchar(20),a2 int,a3 date),然后,修改a1字段的数据类型,由varchar(20)改为varchar(60)。具体操作如下:
mysql> CREATE TABLE test01 ###创建表test01
-> (
-> a1 varchar(20),
-> a2 int,
-> a3 date
-> );
Query OK, 0 rows affected (0.07 sec)
mysql> DESC test01; ###查看表结构
+-------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------+-------------+------+-----+---------+-------+
| a1 | varchar(20) | YES | | NULL | |
| a2 | int(11) | YES | | NULL | |
| a3 | date | YES | | NULL | |
+-------+-------------+------+-----+---------+-------+
3 rows in set (0.01 sec)
mysql> ALTER TABLE test01 MODIFY a1 varchar(60); ###修改字段a1类型
Query OK, 0 rows affected (0.24 sec)
Records: 0 Duplicates: 0 Warnings: 0
mysql> DESC test01;
+-------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------+-------------+------+-----+---------+-------+
| a1 | varchar(60) | YES | | NULL | | ###修改成功
| a2 | int(11) | YES | | NULL | |
| a3 | date | YES | | NULL | |
+-------+-------------+------+-----+---------+-------+
大家考虑一下,是否可以把INT修改为字符型,或把字符型修改整数型?如果要修改需要满足哪些条件?
除了可以修改字段类型,我们还可以修改表名称、字段名称、字段属性等。
4.2.2 修改字段名称
修改字段名称的语句与修改字段类型的不一样,其语法格式为:
ALTER TABLE <表名> CHANGE <旧字段名> <新字段名> <数据类型>;
现在我们把test01表中a1字段名称改为name,数据类型不变。
mysql> desc test01; ###查看表结构
+-------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------+-------------+------+-----+---------+-------+
| a1 | varchar(60) | YES | | NULL | |
| a2 | int(11) | YES | | NULL | |
| a3 | date | YES | | NULL | |
+-------+-------------+------+-----+---------+-------+
mysql> ALTER TABLE test01 CHANGE a1 name varchar(60); ###把字段a1改为name
Query OK, 0 rows affected (0.38 sec)
Records: 0 Duplicates: 0 Warnings: 0
mysql> desc test01;
+-------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------+-------------+------+-----+---------+-------+
| name | varchar(60) | YES | | NULL | | ###修改成功
| a2 | int(11) | YES | | NULL | |
| a3 | date | YES | | NULL | |
+-------+-------------+------+-----+---------+-------+
4.2.3 新增字段
表创建后,根据需要我们可以修改表名、修改表中字段名称、字段类型,当然也可添加字段,而且可以更加指定位置的添加,如果没有指定,缺省是添加到最后。添加字段的语法格式为:
ALTER TABLE <表名> ADD <新增字段名> <字段类型> [字段约束条件][FIRST|AFTER 已有字段名];
我们还是以test01表为例,在name字段后,添加一个名为code的字段,数据类型为varchar(20),并且不能为空或not null。
mysql> ALTER TABLE test01 ADD code varchar(20) not null AFTER name;
Query OK, 0 rows affected (0.17 sec)
Records: 0 Duplicates: 0 Warnings: 0
mysql> desc test01;
+-------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-------+-------------+------+-----+---------+-------+
| name | varchar(60) | YES | | NULL | |
| code | varchar(20) | NO | | NULL | |
| a2 | int(11) | YES | | NULL | |
| a3 | date | YES | | NULL | |
+-------+-------------+------+-----+---------+-------+
4.2.4 修改表的字符集
表的字符集或缺省字符集也能修改?能,这应该也是MySQL特色之一吧,一般数据库系统字符集与数据库绑定在一起,但MySQL把字符集粒度精确到了表甚至字段。虽然这个功能很强大,但也存在很大风险,特别是表中有数据时,可能导致字符类型不兼容问题,为降低风险,还是这句老话,先备份,后修改。
这里的修改一般指修改表的缺省字符集,常用的字符集有:UTF8、GBK、GB2312、latin1等,其中UTF-8用以解决国际上字符的一种多字节编码,它对英文使用8位(即一个字节),中文使用24为(三个字节)来编码。UTF-8包含全世界所有国家需要用到的字符,是国际编码,通用性强。GBK是国家标准GB2312基础上扩容后兼容GB2312的标准。GBK的文字编码是用双字节来表示的,即不论中、英文字符均使用双字节来表示,为了区分中文,将其最高位都设定成1。GBK包含全部中文字符,是国家编码,通用性比UTF8差,不过UTF8占用的数据库比GBK大。
GBK、GB2312等与UTF8不兼容,需要通过Unicode编码才能相互转换:
GBK、GB2312--Unicode--UTF8
UTF8--Unicode--GBK、GB2312 。
字符集涉及面比较广,如服务器或数据库或表字符集、应用字符集(如连接字符集、文件字符集等)、客户端字符,一般这些环节的字符集需要一致或兼容,尤其对中文而言,否则可能导致乱码。如何解决乱码问题,后面我们也有介绍。
以下是修改表的字符集的一个简单实例:
mysql> show create table test01 ; ###查看表存储引擎、字符集等信息
+--------+---------------------------------------------------------------------| Table | Create Table
+--------+---------------------------------------------------------------------| test01 | CREATE TABLE </code>test01<code> (
</code>name<code> varchar(60) DEFAULT NULL,
</code>code<code> varchar(20) NOT NULL,
</code>a2<code> int(11) DEFAULT NULL,
</code>a3<code> date DEFAULT NULL
) ENGINE=InnoDB DEFAULT CHARSET=utf8 | ###缺省字符集为utf8
----------------------------------+
mysql> ALTER TABLE test01 CONVERT TO CHARACTER SET gbk; ###修改缺省字符集为gbk
Query OK, 0 rows affected (0.12 sec)
Records: 0 Duplicates: 0 Warnings: 0
mysql> show create table test01 ; ###检查修改是否成功
+--------+---------------------------------------------------------------------| Table | Create Table
+--------+---------------------------------------------------------------------| test01 | CREATE TABLE </code>test01<code> (
</code>name<code> varchar(60) DEFAULT NULL,
</code>code<code> varchar(20) NOT NULL,
</code>a2<code> int(11) DEFAULT NULL,
</code>a3<code> date DEFAULT NULL
) ENGINE=InnoDB DEFAULT CHARSET=gbk | ###修改成功
修改方式或命令还有很多,大家可以借助其强大的help进一步获取其他命令的使用方法,如可以通过help ALTER TABLE 查询其他使用方法,这里就不在一一例举了。
4.3 插入数据
往表中插入数据,有多种方法,如通过SQL语句、客户端、数据备份工具等。
1)、通过SQL命令:insert into table_name (列1,列2,..) Values(‘’,’’,’’,….);
用这种方法需要注意列与值的对应关系;如果不指定列名,则指所有列:
如insert into table_name values(‘’,’’,’’,…),values(),
2)、通过客户端导入;
3)、利用工具(load data file或mysqlimport等)借助数据文件来导入数据。
这里我们介绍第1种方法,其它2种后面讲数据备份时将介绍。
往表test01插入一条记录。
mysql> select * from test01; ###查看表记录信息
Empty set (0.01 sec)
mysql> INSERT INTO test01(name,code,a2,a3)
-> VALUES('mysql','001',10,'2016-10-30'); ###插入1条记录
Query OK, 1 row affected (0.07 sec)
mysql> select * from test01;
+-------+------+------+------------+
| name | code | a2 | a3 |
+-------+------+------+------------+
| mysql | 001 | 10 | 2016-10-30 | ###插入成功
+-------+------+------+------------+
这是往插入1条记录,如果想一次往表插入多条记录如何实现呢?我们只要在后面添加个values即可,如同时往表中插入2条记录:
insert into table_name values(‘’,’’,’’,…) ,(‘’,’’,’’,…)
注意记录间用逗号。
具体操作请看下例
mysql> INSERT INTO test01(name,code,a2,a3) ###同时插入2条记录
-> VALUES('linux','002',20,'2016-10-30'),
-> ('spark','003',30,'2016-10-30');
Query OK, 2 rows affected (0.06 sec)
Records: 2 Duplicates: 0 Warnings: 0
mysql> select * from test01; ###检查结果,插入成功
+-------+------+------+------------+
| name | code | a2 | a3 |
+-------+------+------+------------+
| mysql | 001 | 10 | 2016-10-30 |
| linux | 002 | 20 | 2016-10-30 |
| spark | 003 | 30 | 2016-10-30 |
+-------+------+------+------------+
第5章 数据类型和运算符
前面介绍创建表结构、往表中插入记录时,涉及数据类型,数据类型对数据质量、性能提升、甚至业务的拓展都有一定关系,在日常使用中经常看到中途修改字段类型的问题,这将带来很大风险,因此,设置合理的数据类型非常重要,我们需要理解各种数据类型及其取值范围,同时也要注意数据类型间的异同。
5.1 数据类型介绍
MySQL支持多种类型,大致可以分为三类:数值、日期/时间和字符串类型。
数值类型
包括整数类型(TINYINT、SMALLINT、MEDIUMINT、INT(或INTEGER)、BIGINT),以及近似数值数据类型,浮点数据类型(FLOAT、DOUBLE)和定位数据类型(DECIMAL或DEC)。
日期时间类型
日期和时间类型有DATETIME、DATE、TIMESTAMP、TIME和YEAR。
字符串类型
字符串类型有CHAR、VARCHAR、BINARY、VARBINARY、BLOB、TEXT等。
5.1.1 数值类型
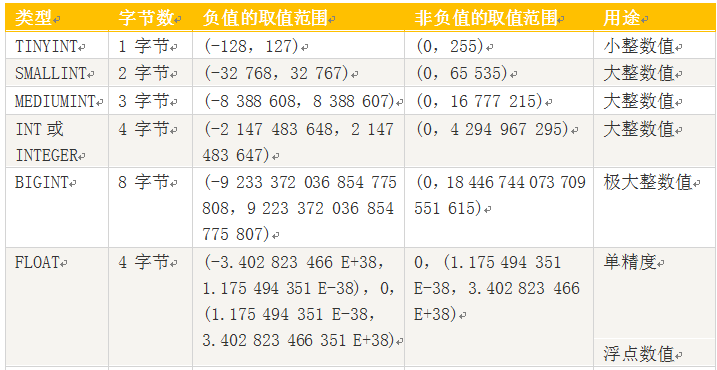
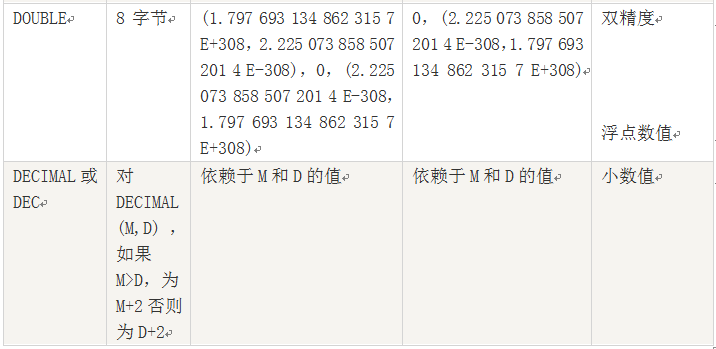
说明:
1、浮点数或定位数,如果实际值超出定义的精度范围,则采用四舍五入进行处理。处理时浮点数不提示,定位数会提示。
2、定位数据以字符串形式存储,如果对精度要求较高的科学计算、货币等,建议使用DECIMAL类型,浮点数进行比较时易出现问题。
3、FLOAT(M,D),其中M参数称为精度,是数据的总长度,即有效数字;D参数成为标度,是指小数点后的长度为D。如FLOAT(5,2)(如213.36)表示数据总长度为2,小数部分长度为2。
5.1.2 日期类型
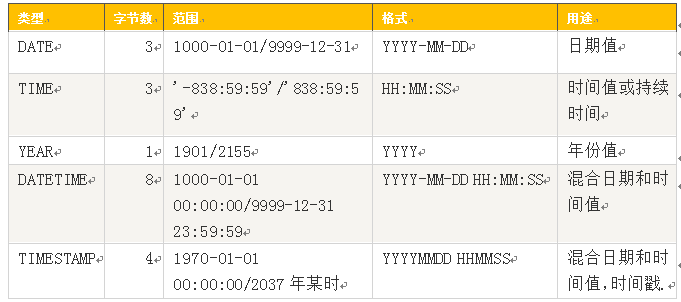
说明:
1、DATETIME和TIMESTAMP虽然都是19位,但前者范围比后者大,具体请看上表。
5.1.3 字符类型
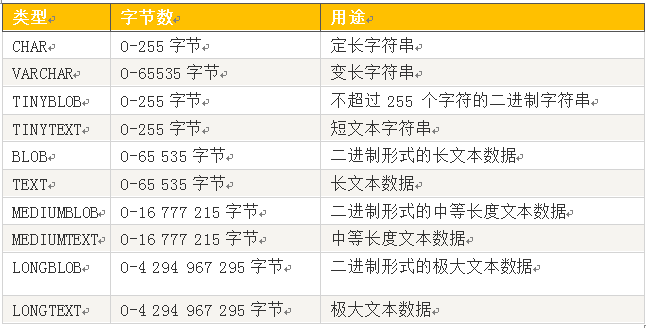
说明:
1、CHAR 把用户定义大小视为值的大小,不长度不足的情况下就用空格补足。而 VARCHAR 类型把它视为最大值并且只使用存储字符串实际需要的长度。
2、因为 VARCHAR 类型可以根据实际内容动态改变存储值的长度,所以在不能确定字段需要多少字符时使用 VARCHAR 类型可以大大地节约磁盘空间、提高存储效率。
5.2 运算符介绍
运算符连接表达式中各个操作数,其作用是用来指明对操作数所进行的运算。常见的运算有数学计算、比较运算、位运算以及逻辑运算。运用运算符可以更加灵活地使用表中的数据,常用的运算符类型有:算术运算符,比较运算符,逻辑运算符等。
算术运算符
包括加(+)、减(-)、乘(*)、除(/)、求于(或称模运算,%)。
比较运算符
包括大于(>)、小于(<)、等于(=)、大于等于(>=)、小于等于(<=)、不等于(!=)、以及IN、 BETWEEN AND、IS NULL、GREATEST、LEAST、LIKE、REGEXP等。 LIKE运算符在进行匹配时,可以使用下面两种通配符: 1.‘%’,匹配任何数目的字符,甚至包括0字符。 2.. ‘_’,只能匹配一个字符。 REGEXP运算符在进行匹配时,常用的有下面几种通配符: 1.‘^’匹配以该字符后面的字符开头的字符串。 2.‘$’匹配以该字符后面的字符结尾的字符串。 3.‘.’匹配任何一个单字符。 4.‘[…]’匹配在方括号内的任何字符。例如,”[abc]”匹配”a”、”b”或”c”。 为了命名字符串的范围,使用一个’-‘。”[a-z]”匹配任何字母,而”[0-9]” 匹配任何数字。 5.‘*’匹配0个或多个在它前面的字符。 逻辑运算符 逻辑非(NOT或者!)、逻辑与(AND或者&&)、逻辑或(OR或者||)、逻辑异或(XOR)。 以下通过一些实例来加深理解:
mysql
> SELECT ISNULL
(NULL
),ISNULL
(12),12 IS NOT NULL
;
+--------------+------------+----------------+
| ISNULL
(NULL
) | ISNULL
(12) |
12 IS NOT NULL |
+--------------+------------+----------------+
|
1 |
0 |
1 |
+--------------+------------+----------------+
1 row
in set (0.06 sec
)
mysql
> SELECT
5 BETWEEN
4 AND
5;
+-------------------+
|
5 BETWEEN
4 AND
5 |
+-------------------+
|
1 |
+-------------------+
1 row
in set (0.04 sec
)
mysql
> SELECT LEAST
(2,3,5),LEAST
('a','b','c'),LEAST
(2,NULL
),GREATEST
(2,NULL
);
+--------------+--------------------+---------------+------------------+
| LEAST
(2,3,5) | LEAST
('a','b','c') | LEAST
(2,NULL
) | GREATEST
(2,NULL
) |
+--------------+--------------------+---------------+------------------+
|
2 | a | NULL | NULL |
+--------------+--------------------+---------------+------------------+
mysql
> SELECT
'ipython'like
'%thon','sql'like
'__l','ok'like NULL
;
+-----------------------+-----------------+---------------+
|
'ipython'like
'%thon' |
'sql'like
'__l' |
'ok'like NULL |
+-----------------------+-----------------+---------------+
|
1 |
1 | NULL |
+-----------------------+-----------------+---------------+
1 row
in set (0.00 sec
)
mysql
> SELECT
'spark'REGEXP
'^s','10$'REGEXP
' ,'spark'REGEXP '[abc]';
,'spark'REGEXP '[abc]';
+--------------------+------------------+-----------------------+
| 'spark'REGEXP '^s' | '10$'REGEXP '" />' |
'spark'REGEXP
'[abc]' |
+--------------------+------------------+-----------------------+
|
1 |
1 |
1 |
+--------------------+------------------+-----------------------+
第6章 查询数据
数据库主要功能是存储数据,但存储数据不是最终目的,存储数据最终目的是为了展示和分析,如何分析展示数据库中数据,数据查询就是重要手段。MySQL提供了功能强大、又非常灵活、非常方便的语句实现这些操作。这一章将介绍使用SELECT语句实现简单查询、子查询、连接查询、分组查询及利用正则表达式查询等。
6.1 一般查询语句
最简单的是SELECT [列名]FROM [表名] WHERE [条件] 。然后你可以在后面加上像[LIMIT][ORDER BY][GROUP BY][HAVING]等。
[列名]: 可以多个字段(列间用逗号分隔),也可所以字段(一般用*表示所有字段)
[表名]: 可以是一个表名或视图名,也可以是多表或多视图(表间用逗号分隔)。
[条件]: 为可选项,如果选择该项,将限制行必须满足的查询条件。
[LIMIT]: 后跟[位置偏移量,] 行数 (第1行的位置偏移量为0,第2行为1,以此类推。)
[ORDER BY]: 后跟字段,可一个或多个,根据这些字段进行分组。
[GROUP BY]: 后跟可一个或多个字段,根据这些字段进行排序,升序(ASC)或降序(DESC)。
其后也可跟WITH ROLLUP,增加一条合计记录。
[HAVING]: 一般与GROUP BY一起使用,用来显示满足条件的分组记录。
6.2 单表查询
单表查询就是从1张表中查询数据,后续将介绍多表查询。为查询表数据我们需要先做些准备工作。
6.2.1 准备工作
准备工作包括:1)、定义表结构,创建表;2)、查看分析数据文件;3).把数据导入到表中。
1).首先我们创建一个存储学生各科成绩的表(stud_score),表的定义如下:
(表6-1 学生成绩表 stud_score)

转换为建表的SQL语句为:
DROP TABLE IF EXISTS stud_score;
CREATE TABLE stud_score (
stud_code varchar(20) NOT NULL,
sub_code varchar(20) NOT NULL,
sub_name varchar(100) default NULL,
sub_tech varchar(20) default NULL COMMENT '教师代码',
sub_score smallint(10) default NULL,
stat_date date default NULL,
PRIMARY KEY (stud_code,sub_code)
);
2)、创建这个表以后,我们需要把一个包含该表数据的文件(在slave02节点的/tmp目录下,名称为stud_score.csv)导入该表,另该文件第1行为字段名称,需过滤掉。我们先操作,具体语法等我们后续会介绍。
查看该数据文件信息
hadoop@master:/tmp$ pwd
/tmp
hadoop@master:/tmp$ ls -l |grep 'stud*'
-rw-rw-r-- 1 feigu feigu 1508 Jul 6 15:47 stud_info.csv
-rw-rw-rw- 1 mysql mysql 7157 Jul 2 11:32 stud_score_0702.txt
-rw-rw-rw- 1 mysql mysql 7157 Jul 2 21:43 stud_score_0703.txt
-rw-rw-r-- 1 feigu feigu 4652 Jul 2 10:26 stud_score.csv
hadoop@master:/tmp$ head -2 stud_score.csv
stud_code,sub_code,sub_nmae,sub_tech,sub_score,stat_date
2015101000,10101,数学分析,,90,
hadoop@master:/tmp$ cat stud_score.csv |wc -l ###查看文件记录总数
122
3)、把数据文件导入表中
mysql> DROP TABLE IF EXISTS stud_score; ###判断是否存在,存在则删除
Query OK, 0 rows affected (0.36 sec)
mysql> CREATE TABLE stud_score ( ###创建表
-> stud_code varchar(20) NOT NULL,
-> sub_code varchar(20) NOT NULL,
-> sub_name varchar(100) default NULL,
-> sub_tech varchar(20) default NULL COMMENT '教师代码',
-> sub_score smallint(10) default NULL,
-> stat_date date default NULL,
-> PRIMARY KEY (stud_code,sub_code)
-> );
Query OK, 0 rows affected (0.07 sec)
mysql> select * from stud_score; ###查看是否有数据
Empty set (0.00 sec)
mysql> load data infile '/tmp/stud_score.csv' into table stud_score fields terminated by "," ignore 1 lines; ###把数据导入到表中
Query OK, 121 rows affected, 121 warnings (0.25 sec)
Records: 121 Deleted: 0 Skipped: 0 Warnings: 121
mysql> select count(*) from stud_score; ###查看验证记录总数
+----------+
| count(*) |
+----------+
| 121 |
+----------+
1 row in set (0.07 sec)
6.2.2 查看指定行数据
mysql> SELECT * FROM stud_score where sub_name='高等代数'; ###查看指定学科
+------------+----------+--------------+----------+-----------+------------+
| stud_code | sub_code | sub_name | sub_tech | sub_score | stat_date |
+------------+----------+--------------+----------+-----------+------------+
| 2015101000 | 10102 | 高等代数 | | 88 | 0000-00-00 |
| 2015101001 | 10102 | 高等代数 | | 78 | 0000-00-00 |
| 2015101002 | 10102 | 高等代数 | | 97 | 0000-00-00 |
| 2015101003 | 10102 | 高等代数 | | 87 | 0000-00-00 |
| 2015101004 | 10102 | 高等代数 | | 77 | 0000-00-00 |
| 2015101005 | 10102 | 高等代数 | | 65 | 0000-00-00 |
| 2015101006 | 10102 | 高等代数 | | 68 | 0000-00-00 |
| 2015101007 | 10102 | 高等代数 | | 80 | 0000-00-00 |
| 2015101008 | 10102 | 高等代数 | | 96 | 0000-00-00 |
| 2015101009 | 10102 | 高等代数 | | 79 | 0000-00-00 |
| 2015101010 | 10102 | 高等代数 | | 52 | 0000-00-00 |
+------------+----------+--------------+----------+-----------+------------+
mysql> SELECT * FROM stud_score LIMIT 3; ###查看前3行
+------------+----------+--------------+----------+-----------+------------+
| stud_code | sub_code | sub_name | sub_tech | sub_score | stat_date |
+------------+----------+--------------+----------+-----------+------------+
| 2015101000 | 10101 | 数学分析 | | 90 | 0000-00-00 |
| 2015101000 | 10102 | 高等代数 | | 88 | 0000-00-00 |
| 2015101000 | 10103 | 大学物理 | | 67 | 0000-00-00 |
+------------+----------+--------------+----------+-----------+------------+
3 rows in set (0.00 sec)
mysql> SELECT * FROM stud_score LIMIT 2, 2; ###查看第3行开始后2行
+------------+----------+-----------------+----------+-----------+------------+
| stud_code | sub_code | sub_name | sub_tech | sub_score | stat_date |
+------------+----------+-----------------+----------+-----------+------------+
| 2015101000 | 10103 | 大学物理 | | 67 | 0000-00-00 |
| 2015101000 | 10104 | 计算机原理 | | 78 | 0000-00-00 |
+------------+----------+-----------------+----------+-----------+------------+
2 rows in set (0.00 sec)
6.2.3 模糊查询
利用LIKE 关键字可以进行模糊查询。下例查询学科代码以101开头的记录总数。
mysql> SELECT count(*) FROM stud_score WHERE sub_code LIKE '101%';
+----------+
| count(*) |
+----------+
| 55 |
+----------+
mysql>select * from stud_info where birthday REGEXP '^1998' ;
mysql> select * from stud_info where birthday REGEXP '10$' ;
6.2.4 分组查询
如果我们希望按学科来统计学生成绩、班级成绩该如何实现呢?这就涉及到分组统计问题,如果需要按学科统计,可以GROUP BY sub_code;然后取前3名学科,具体实现请看下例:
mysql> SELECT sub_code,SUM(sub_score) from stud_score GROUP BY sub_code;
+----------+----------------+
| sub_code | SUM(sub_score) |
+----------+----------------+
| 10101 | 863 |
| 10102 | 867 |
| 10103 | 830 |
| 10104 | 932 |
| 10105 | 857 |
| 20101 | 870 |
| 20102 | 892 |
| 20103 | 866 |
| 20104 | 864 |
| 20105 | 822 |
| 20106 | 843 |
+----------+----------------+
11 rows in set (0.00 sec)
mysql> SELECT sub_code,SUM(sub_score) AS sum_score from stud_score GROUP BY sub_code
-> ORDER BY sum_score DESC LIMIT 3; ###按学科总分排序,取前3。
+----------+-----------+
| sub_code | sum_score |
+----------+-----------+
| 10104 | 932 |
| 20102 | 892 |
| 20101 | 870 |
+----------+-----------+
6.3 多表查询
多表查询,需要连接2张或2张以上的表一起查询,连接有多种方式,如内连接(通常缺省连接)、外链接(又分为左连接,右连接)等。多表连接时,建议不宜一下连接很多表,尤其是数据比较大时,可以采用两两连接等方式。
要实现多表连接,还需创建一个存储学生基本信息的表(stud_info)并导入数据.
6.3.1 准备工作
创建一个学生基本信息的表(表定义如下),并把数据(一个数据文件)导入到表中。
准备步骤,1).定义并创建表,2),查看分析数据文件,3). 导入数据,并验证导入结果。
1).定义并创建表

mysql> CREATE TABLE stud_info (
-> stud_code varchar(20) NOT NULL,
-> stud_name varchar(100) NOT NULL,
-> stud_sex char(1) NOT NULL default 'M' COMMENT '性别',
-> birthday date default NULL,
-> log_date date default NULL,
-> orig_addr varchar(100) default NULL,
-> lev_date date default NULL,
-> college_code varchar(10) default NULL COMMENT '学院编码',
-> college_name varchar(100) default NULL,
-> state varchar(10) default NULL,
-> PRIMARY KEY (stud_code)
-> ) ;
Query OK, 0 rows affected (0.05 sec)
2).查看分析数据文件
hadoop@master:/tmp$ ls -l|grep 'stud_info*'
-rw-rw-r-- 1 feigu feigu 1508 Jul 6 15:47 stud_info.csv
hadoop@master:/tmp$ cat stud_info.csv|wc -l ###查看文件记录总数
23
hadoop@master:/tmp$ head -3 stud_info.csv ###查看前3行
stud_code,stud_name,stud_gend,birthday,log_date,orig_addr,lev_date,college_code,college_name,state
2015101000,王进,M,1997/8/1,2014/9/1,苏州,,10,理学院,1
2015101001,刘海,M,1997/9/29,2014/9/1,上海,,10,理学院,1
3).导入数据并验证结果
mysql> select count(*) from stud_info; ###查看表数据
+----------+
| count(*) |
+----------+
| 0 |
+----------+
1 row in set (0.00 sec)
mysql> load data infile '/tmp/stud_info.csv' into table stud_info fields terminated by "," ignore 1 lines;
Query OK, 22 rows affected, 22 warnings (0.05 sec)
Records: 22 Deleted: 0 Skipped: 0 Warnings: 22
mysql> select count(*) from stud_info; ###成功导入22条记录
+----------+
| count(*) |
+----------+
| 22 |
+----------+
1 row in set (0.00 sec)
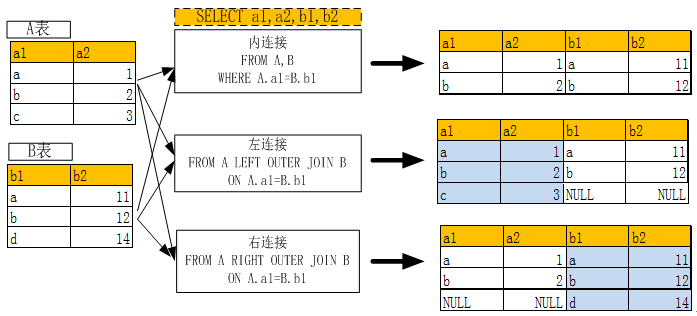
6.3.2 多表连接查询
两表内连接、左连接,右连接的含义及使用关键字请参看下图:
(图6-1 多表连接示意图)
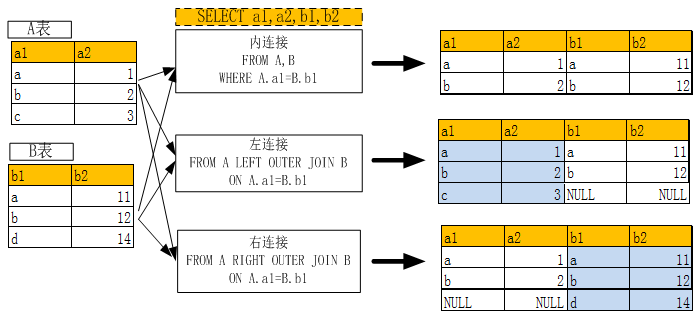
以下通过几个实例进一步说明多表连接的使用方法:
mysql> SELECT a.stud_name,b.sub_name,b.sub_score FROM stud_info a,stud_score b WHERE a.stud_code=b.stud_code LIMIT 3; ###内连接,a定义为stud_info表的别名。
+-----------+--------------+-----------+
| stud_name | sub_name | sub_score |
+-----------+--------------+-----------+
| 王进 | 数学分析 | 90 |
| 王进 | 高等代数 | 88 |
| 王进 | 大学物理 | 67 |
+-----------+--------------+-----------+
mysql> SELECT a.stud_name,b.sub_name,b.sub_score FROM stud_info a LEFT OUTER JOIN stud_score b ON a.stud_code=b.stud_code LIMIT 3; ###左连接
+-----------+--------------+-----------+
| stud_name | sub_name | sub_score |
+-----------+--------------+-----------+
| 王进 | 数学分析 | 90 |
| 王进 | 高等代数 | 88 |
| 王进 | 大学物理 | 67 |
+-----------+--------------+-----------+
3 rows in set (0.00 sec)
mysql> SELECT a.stud_name,b.sub_name,b.sub_score FROM stud_info a RIGHT OUTER JOIN stud_score b ON a.stud_code=b.stud_code LIMIT 3; ###右连接
+-----------+--------------+-----------+
| stud_name | sub_name | sub_score |
+-----------+--------------+-----------+
| 王进 | 数学分析 | 90 |
| 王进 | 高等代数 | 88 |
| 王进 | 大学物理 | 67 |
+-----------+--------------+-----------+
3 rows in set (0.00 sec)
6.3.3 子连接查询
这里介绍以用IN关键字实现子链接,基本格式为:
SELECT * FROM 表名WHERE 字段 IN (SELECT 字段 FROM 表名 WHERE 条件);
使用子查询,比较灵活,且有利于把大表关联转换为小表关联。下例为表stud_info中
stud_code从表stud_score中成绩为大于或等于90分的子查询中获取。
mysql> SELECT stud_name FROM stud_info WHERE stud_code IN(SELECT stud_code FROM stud_score WHERE sub_score>=90 ) LIMIT 3;
+-----------+
| stud_name |
+-----------+
| 王进 |
| 刘海 |
| 张飞 |
+-----------+
3 rows in set (0.02 sec)
6.3.4 视图查询
上面的查询语句,有的比较简单,有的比较复杂,像对那些复杂的查询语句,包含了很多信息量,而且有可能还要经常使用,但命令行是无法保证这些语句的,如果下次还要使用是否又重新写一遍呢?大可不必,我们可以把这个查询语句以视图的形式保存到数据库中,然后直接查询这个视图即可。
如上面内连接的SQL语句:SELECT a.stud_name,b.sub_name,b.sub_score FROM stud_info a,stud_score b WHERE a.stud_code=b.stud_code LIMIT 3;
我们可以把它定义为一个视图V_STUD,然后查询视图即可,非常方便!而且视图会保存到数据库中,但视图本身不保存数据。具体实现请看下例:
mysql> CREATE VIEW V_STUD AS SELECT a.stud_name,b.sub_name,b.sub_score FROM stud_info a,stud_score b WHERE a.stud_code=b.stud_code LIMIT 3; ###创建视图
Query OK, 0 rows affected (0.00 sec)
mysql> SELECT * FROM V_STUD; ###查询视图
+-----------+--------------+-----------+
| stud_name | sub_name | sub_score |
+-----------+--------------+-----------+
| 王进 | 数学分析 | 90 |
| 王进 | 高等代数 | 88 |
| 王进 | 大学物理 | 67 |
+-----------+--------------+-----------+
3 rows in set (0.00 sec)
第7章 增删改数据
存储数据时用来查询分析用的,所以查询分析数据是平时重要任务,但数据库中数据它不会自动生成,需要我们去维护,当然大部分是系统自动维护,不需要手工去操作,不过维护程序还是需要写的,这章我们介绍如何维护数据库数据。这里我们主要介绍如何新增数据、如何修改数据、如何删除数据等。
7.1 插入数据
插入数据语句的语法:
INSERT INTO 表名[(列名1,……列名n)] values(值1,…..值n);
这个SQL语句一次往表中插入1条记录,如果一次要插入多条记录是否可以呢?可以,而且很方便,插入多条语句为:
INSERT INTO 表名[(列名1,……列名n)] VALUES(值1,…..值n), (值1,…..值n),..;
下面我们还是通过一些实例来进步说明如何操作。
mysql> CREATE TABLE test03 (id INT NOT NULL,name VARCHAR(20),birthday DATE);
Query OK, 0 rows affected (0.17 sec)
mysql> DESC TEST03; ###查看表结构
ERROR 1146 (42S02): Table 'testdb.TEST03' doesn't exist
mysql> DESC test03;
+----------+-------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+----------+-------------+------+-----+---------+-------+
| id | int(11) | NO | | NULL | |
| name | varchar(20) | YES | | NULL | |
| birthday | date | YES | | NULL | |
+----------+-------------+------+-----+---------+-------+
3 rows in set (0.04 sec)
mysql> INSERT INTO test03 VALUES(100,'张华', '2000-01-01'); ##对所有字段插值
Query OK, 1 row affected (0.16 sec)
mysql> INSERT INTO test03(id,name) VALUES(200,'刘婷'); ###选择字段插值
Query OK, 1 row affected (0.13 sec)
mysql> SELECT * FROM test03;
+-----+--------+------------+
| id | name | birthday |
+-----+--------+------------+
| 100 | 张华 | 2000-01-01 |
| 200 | 刘婷 | NULL |
+-----+--------+------------+
2 rows in set (0.00 sec)
mysql> INSERT INTO test03(id,name) VALUES(300,'貂蝉'),(400,'吕布'); ##插入多条
Query OK, 2 rows affected (0.03 sec)
Records: 2 Duplicates: 0 Warnings: 0
7.2 修改数据
修改数据也是很常见的,不过修改数据前,记得备份数据。如何备份数据后面将介绍。
修改数据的一般语法:
UPDATE 表名 SET 列名1=值1,….列名n=值n
[WHERE 条件];
以下以修改id为200对应的name为例,假设发现id为200对应的name输错了,不是刘婷,而是刘涛。
mysql> UPDATE test03 SET name='刘涛' WHERE id=200; ###修改id对应name值
Query OK, 1 row affected (0.02 sec)
Rows matched: 1 Changed: 1 Warnings: 0
mysql> SELECT * FROM test03 WHERE id=200; ###查询验证结果
+-----+--------+----------+
| id | name | birthday |
+-----+--------+----------+
| 200 | 刘涛 | NULL | ###修改成功
+-----+--------+----------+
1 row in set (0.00 sec)
7.3 删除数据
删除数据时,我们可以选择删除几条,或满足某些条件的记录,当然也可以删除所有记录。在日常工作中,删除数据需要非常谨慎,务必养成一个良好习惯,先备份,后删除。对生产环境数据、或正式环境的数据,不建议物理删除,最好采用逻辑删除的方式(即修改对应记录的状态或有效时间等)。数据都有价值。
用DELETE删除数据的一般语法:
DELETE FROM 表名 [WHERE 条件];
DELETE 加上条件,就可以有条件删除记录;如果没有条件,将删除所有数据。删除所有数据也可用TRUNCATE命令(这种方式删除数据比较快),其命令格式为:
TRUNCATE [table] 表名;
使用DELETE FROM 表名或TRUNCATE [table] 表名命令删除全部记录时,有一种情况需要注意,如果一个表中有自增字段,这个自增字段将起始值恢复成1.如果你不想这样做的话,可以在DELETE语句中加上永真的WHERE,如WHERE 1或WHERE true。
mysql> SELECT * FROM test03;
+-----+--------+------------+
| id | name | birthday |
+-----+--------+------------+
| 100 | 张华 | 2000-01-01 |
| 200 | 刘涛 | NULL |
| 300 | 貂蝉 | NULL |
| 400 | 吕布 | NULL |
+-----+--------+------------+
4 rows in set (0.00 sec)
mysql> DELETE FROM test03 WHERE (id=300 or id=400);
Query OK, 2 rows affected (0.02 sec)
mysql> SELECT * FROM test03;
+-----+--------+------------+
| id | name | birthday |
+-----+--------+------------+
| 100 | 张华 | 2000-01-01 |
| 200 | 刘涛 | NULL |
+-----+--------+------------+
2 rows in set (0.00 sec)
mysql> DELETE FROM test03;
Query OK, 2 rows affected (0.01 sec)
mysql> SELECT * FROM test03;
Empty set (0.00 sec)
7.4 删除含自增字段的表
CREATE TABLE person
(
id INT UNSIGNED NOT NULL AUTO_INCREMENT,
name CHAR(40) NOT NULL DEFAULT '',
age INT NOT NULL DEFAULT 0,
info CHAR(50) NULL,
PRIMARY KEY (id)
);
【1】在person表中,插入一条新记录,列的顺序与表一致,SQL语句如下:
INSERT INTO person (id ,name, age , info) VALUES (1,'Green', 21, 'Lawyer');
【2】在person表中,插入一条新记录,列顺序与表不一致,SQL语句如下:
INSERT INTO person (age ,name, id , info)
VALUES (22, 'Suse', 2, 'dancer');
【3】在person表中,插入一条新记录,不写列名,SQL语句如下:
INSERT INTO person VALUES (3,'Mary', 24, 'Musician');
【4】在person表中,插入一条新记录,不写自增字段,SQL语句如下:
INSERT INTO person (name, age,info) VALUES('Willam', 20, 'sports man');
【5】在person表中,插入一条新记录,不写id、age,SQL语句如下:
INSERT INTO person (name, info ) VALUES ('Laura', 'teacher');
【6】在person表中,在name、age和info字段指定插入值,同时插入3条新记录,SQL语句如下:
INSERT INTO person(name, age, info)
VALUES ('Evans',27, 'secretary'),
('Dale',22, 'cook'),
('Edison',28, 'singer');
【7】在person表中,不指定插入列表,同时插入2条新记录,SQL语句如下:
INSERT INTO person
VALUES (9,'Harry',21, 'magician'),
(NULL,'Harriet',19, 'pianist');
【8】在person表中,delete 全表然后看自增字段的值,SQL语句如下
show table status like 'person';
delete from person;
truncate table person;
show table status like 'person';
修改自动增长字段起始值
alter table person auto_increment = 100 ;
INSERT INTO person (name, age,info) VALUES('Willam', 20, 'sports man');
select * from person;
7.5 事务控制
在mysql中不同存储引擎对锁的粒度不同,InnoDB可到行级,MyISAM和MEMORY可到表级,BDB可到页级,下面以InnoDB引擎为例,说明MySQL的锁及事务控制。
给表加锁
session1 session2
给表加锁
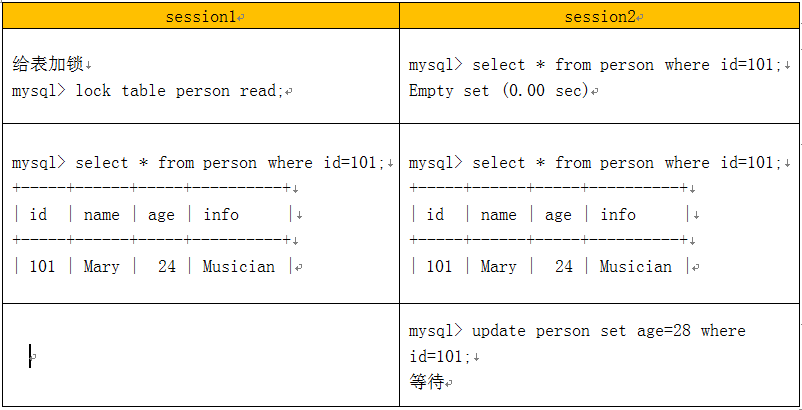

事务控制实例:


事务控制及回滚





第8章 MySQL函数
MySQL数据库自身带有很多函数,合理使用这些函数能有效提高我们的编程效率和编程质量,可以直接使用数据库自带函数(或称为内置函数),当然我们也可以根据自己需要自定义函数。自定义函数(UDF)后面将介绍。
8.1 函数简介
MySQL提供了大量函数,具体可为:数学函数、字符串函数、日期及时间函数、聚合函数、条件判断函数、系统信息函数等等。这些函数极大丰富和增强了对数据的处理和分析能力。下面我们就一些常用的函数进行说明,大家也可通过help或网络查看MySQL函数的一些使用方法。
8.2 数学函数
ABS(x)
返回x的绝对值
MOD(x,y)
返回x/y的模(余数)
RAND()
返回0到1内的随机值,可以通过提供一个参数(种子),如RAND(N)使RAND() 随机数生成器生成一个指定的值。
SQRT(x)
返回一个数的平方根。
ROUND(X)
返回参数X的四舍五入的一个整数。
mysql> SELECT ABS(10),ABS(-20);
+---------+----------+
| ABS(10) | ABS(-20) |
+---------+----------+
| 10 | 20 |
+---------+----------+
1 row in set (0.00 sec)
mysql> SELECT MOD(10,3),RAND(),RAND(),RAND(2),RAND(2);
+-----------+--------------------+---------------------+--------------------+
| MOD(10,3) | RAND() | RAND() | RAND(2) | RAND(2) |
+-----------+--------------------+---------------------+--------------------+
| 1 | 0.8742189052274627 | 0.21504458060026596 | 0.6555866465490187 | 0.6555866465490187 |
+-----------+--------------------+---------------------+--------------------+
1 row in set (0.00 sec)
mysql> SELECT SQRT(4),SQRT(5),ROUND(SQRT(5));
+---------+------------------+----------------+
| SQRT(4) | SQRT(5) | ROUND(SQRT(5)) |
+---------+------------------+----------------+
| 2 | 2.23606797749979 | 2 |
+---------+------------------+----------------+
8.3 字符串函数
CONCAT(str1,str2,...)
返回来自于参数连结的字符串。如果任何参数是NULL,返回NULL。可以 有超过2个的参数。一个数字参数被变换为等价的字符串形式。
LOWER(str)
返回将字符串str中所有字符改变为小写后的结果
LEFT(str,x)
返回字符串str中最左边的x个字符
LENGTH(s)
返回字符串str中的字符数
LTRIM(str)
从字符串str中切掉开头的空格
LOCATE(substr,str)
返回子串substr在字符串str中第一次出现的位置
REVERSE(str)
返回颠倒字符串str的结果
RIGHT(str,x)
返回字符串str中最右边的x个字符
RTRIM(str)
返回字符串str尾部的空格
STRCMP(s1,s2)
比较字符串s1和s2
TRIM(str)
去除字符串首部和尾部的所有空格
SBUSTR(str,pos)
就是从pos开始的位置,一直截取到最后。
SUBSTR(str,pos,len)
就是从pos开始的位置,截取len个字符(空白也算字符)
UPPER(str)
返回将字符串str中所有字符转变为大写后的结果
mysql> SELECT CONCAT('My','SQL');
+--------------------+
| CONCAT('My','SQL') |
+--------------------+
| MySQL |
+--------------------+
mysql> SELECT LOCATE('SQL','Spark SQL');
+---------------------------+
| LOCATE('SQL','Spark SQL') |
+---------------------------+
| 7 |
+---------------------------+
mysql> SELECT TRIM(' Python ');
+--------------------+
| TRIM(' Python ') |
+--------------------+
| Python |
+--------------------+
mysql> SELECT SUBSTR('Hadoop V2.8',8),SUBSTR('Hadoop V2.8',6,4),SUBSTR('Hadoop V2.8',-4,4);
+-------------------------+---------------------------+-----------------------
| SUBSTR('Hadoop V2.8',8) | SUBSTR('Hadoop V2.8',6,4) | SUBSTR('Hadoop V2.8',-4,4)|
+-------------------------+---------------------------+-----------------------
| V2.8 | p V2 | V2.8
+-------------------------+---------------------------+------------------------
mysql> select stud_name,substr(stud_name,2,1),length(stud_name),char_length(stud_name) from stud_info;
+-----------+-----------------------+-------------------+------------------------+
| stud_name | substr(stud_name,2,1) | length(stud_name) | char_length(stud_name) |
+-----------+-----------------------+-------------------+------------------------+
| 王进 | 进 | 6 | 2 |
| 刘海 | 海 | 6 | 2 |
| 张飞 | 飞 | 6 | 2 |
| 刘婷 | 婷 | 6 | 2 |
| 卢家 | 家 | 6 | 2 |
| 韩林 | 林 | 6 | 2 |
| 张景和 | 景 | 9 | 3 |
| 刘芳菲 | 芳 | 9 | 3 |
8.4 日期和时间函数
CURRENT_DATE()
返回当前的日期
CURRENT_TIME()
返回当前的时间
NOW()
返回当前的日期和时间
DATE_ADD(date,INTERVAL int keyword)
返回日期date加上间隔时间int的结果(int必须按 照关键字进行格式化), 如:SELECTDATE_ADD(CURRENT_DATE,INTERVAL 6 MONTH);
DATE_FORMAT(date,fmt)
依照指定的fmt格式格式化日期date值
mysql> SELECT CURRENT_DATE(),CURRENT_TIME(),NOW();
+----------------+----------------+---------------------+
| CURRENT_DATE() | CURRENT_TIME() | NOW() |
+----------------+----------------+---------------------+
| 2016-11-01 | 15:06:57 | 2016-11-01 15:06:57 |
+----------------+----------------+---------------------+
mysql> SELECT CURRENT_DATE,DATE_ADD(CURRENT_DATE,INTERVAL 5 DAY);
+--------------+---------------------------------------+
| CURRENT_DATE | DATE_ADD(CURRENT_DATE,INTERVAL 5 DAY) |
+--------------+---------------------------------------+
| 2016-11-01 | 2016-11-06 |
+--------------+---------------------------------------+
mysql> SELECT DATE_FORMAT(CURRENT_DATE,'%Y %m %d');
+--------------------------------------+
| DATE_FORMAT(CURRENT_DATE,'%Y %m %d') |
+--------------------------------------+
| 2016 11 01 |
+--------------------------------------+
8.5 聚合函数
什么叫聚合计算?举个简单例子大家就明白了,假如要统计一个班男女同学各多少,这个问题就是聚合计算,聚合统计实际上就是分组计算或分组统计。以下通过图形来说明根据课程来分组聚合计算课程成绩的详细过程:
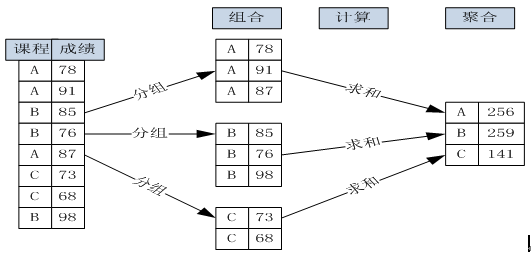
(图 8-1 按课程分组与聚合成绩的计算过程)
数据库如何进行聚合计算?非常方便,MySQL提供了现成的语句,即GROUP BY,具体格式为:
SELECT 聚合函数(如COUNT、SUM等) FROM 表名称 GROUP BY 分组字段(可以1个或多个)。
常用于GROUP BY从句的SELECT查询中。
AVG(col) 返回指定列的平均值
COUNT(col) 返回指定列中非NULL值的个数
MIN(col) 返回指定列的最小值
MAX(col) 返回指定列的最大值
SUM(col) 返回指定列的所有值之和
mysql> SELECT sub_name,AVG(sub_score),SUM(sub_score),COUNT(sub_score) FROM stud_score GROUP BY sub_code;
+--------------------------+----------------+----------------+------------------+
| sub_name | AVG(sub_score) | SUM(sub_score) | COUNT(sub_score) |
+--------------------------+----------------+----------------+------------------+
| 数学分析 | 78.4545 | 863 | 11 |
| 高等代数 | 78.8182 | 867 | 11 |
| 大学物理 | 75.4545 | 830 | 11 |
| 计算机原理 | 84.7273 | 932 | 11 |
+--------------------------+----------------+----------------+------------------+
8.6 条件判断函数
IFNULL(expr1,expr2)
如果expr1不是NULL,IFNULL()返回expr1,否则它返回expr2。
IF(expr1,expr2,expr3)
如果expr1是TRUE(expr1<>0且expr1<>NULL),那么返回expr2,否则它 返回expr3。
CASE value WHEN [compare-value] THEN result [WHEN [compare-value] THEN result ...] [ELSE result] END
CASE WHEN [condition] THEN result [WHEN [condition] THEN result ...] [ELSE result] END
如果第一个条件为真,返回result。如果没有匹配的result值,那么结 果在ELSE后的result被返回。如果没有ELSE部分,那么NULL被返回。
mysql> SELECT IFNULL(1,2),IFNULL(NULL,2);
+-------------+----------------+
| IFNULL(1,2) | IFNULL(NULL,2) |
+-------------+----------------+
| 1 | 2 |
+-------------+----------------+
mysql> SELECT IF(2>1,2,1),IF(2<1,2,1),IF(TRUE,10,100); +-------------+-------------+-----------------+ | IF(2>1,2,1) | IF(2<1,2,1) | IF(TRUE,10,100) | +-------------+-------------+-----------------+ | 2 | 1 | 10 | +-------------+-------------+-----------------+ mysql> SELECT sub_name,
-> CASE
-> WHEN AVG(sub_score)>=90 THEN '优'
-> WHEN AVG(sub_score)>=80 AND AVG(sub_score) ELSE '合格'END as level
-> FROM stud_score GROUP BY sub_code
-> ORDER BY AVG(sub_score) DESC
-> LIMIT 5;
+--------------------------+--------+
| sub_name | level |
+--------------------------+--------+
| 计算机原理 | 良 |
| 计算机系统结构 | 良 |
| 计算机软件与理论 | 合格 |
| 高等代数 | 合格 |
| 操作系统 | 合格 |
+--------------------------+--------+
5 rows in set (0.09 sec)
8.7 系统信息函数
DATABASE() 返回当前数据库名
CONNECTION_ID() 返回当前客户的连接ID
FOUND_ROWS() 返回最后一个SELECT查询进行检索的总行数
USER() 返回当前登陆用户名
VERSION() 返回MySQL服务器的版本
mysql> SELECT FOUND_ROWS(),USER(),VERSION() ;
+--------------+-----------------------+-------------------------+
| FOUND_ROWS() | USER() | VERSION() |
+--------------+-----------------------+-------------------------+
| 5 | feigu@master | 5.5.40-0ubuntu0.14.04.1 |
+--------------+-----------------------+-------------------------+
第9章 存储过程与函数
存储过程或函数,有啥作用?如果我们平时只是使用一些简单SQL,可能不需要用到它们,如果那天你需要编写一个多功能、比较复杂的SQL,它们的作用就不可小看了。特别是一些功能需要提交到生产环境,那就更离不开它们了。这个有点像shell中命令与脚本一样。脚本可以把很多命令写到一个文件中,而且这个脚本可以放到其他服务器,可以定时执行等等,非常方便。
实际上MySQL的存储过程或函数还有些特殊有点。我们常用的操作数据库语言SQL语句在执行的时候需要要先编译,然后执行,而存储过程(Stored Procedure)是一组为了完成特定功能的SQL语句集,经编译后存储在数据库中,用户通过指定存储过程的名字并给定参数(如果该存储过程带有参数)来调用执行它。而且执行都在数据库中,可减少数据在数据库与应用服务间的传输,既可节省网络资源,又可提高运行效率。
存储过程与函数的区别可从以下几个方面来比较:
返回值:存储过程没有,但函数必须有。
参数: 存储过程有IN,OUT,INOUT类型,函数只有IN类型。
调用: CALL 存储过程名(参数),SELECT 函数名(参数)
9.1 创建存储过程或函数
创建或修改存储过程或函数的语法如下:
CREATE PROCEDURE 过程名 ([过程参数[,...]])
[特性 ...] 过程体
CREATE FUNCTION 函数名称([参数列表[,..]])
RETURNS 返回值类型
以下存储过程输入学生代码,统计该学生所选课程总数,并输出。
mysql> DELIMITER // ##定义存储过程结束符为://
mysql> DROP PROCEDURE if EXISTS p_stat_score ;
-> CREATE PROCEDURE p_stat_score(IN i_stud_code VARCHAR(20),OUT o_count INT)
-> BEGIN
-> SELECT count(*) INTO o_count FROM stud_score WHERE stud_code =i_stud_code;
-> END//
Query OK, 0 rows affected, 1 warning (0.00 sec)
mysql> DELIMITER ; ###恢复结束符
mysql> CALL p_stat_score(2015101000,@count); ###执行存储过程
Query OK, 1 row affected (0.00 sec)
mysql> SELECT @count;
+--------+
| @count |
+--------+
| 5 |
+--------+
上面这个存储过程的功能,如何用函数来实现呢?
mysql> DROP FUNCTION if EXISTS f_stat_score ;
-> CREATE FUNCTION f_stat_score(i_stud_code VARCHAR(20))
-> RETURNS INT
-> BEGIN
-> DECLARE o_count INT; ###定义保存返回值变量
-> set @s1=1; ###定义用户变量,用来调试
-> SELECT count(*) INTO o_count FROM stud_score WHERE stud_code =i_stud_code;
-> set @s2=2;
-> RETURN o_count;
-> END//
Query OK, 0 rows affected (0.00 sec)
mysql> DELIMITER ;
mysql> SELECT f_stat_score(2015101000);
+--------------------------+
| f_stat_score(2015101000) |
+--------------------------+
| 5 |
+--------------------------+
1 row in set (0.00 sec)
mysql> SELECT @s1,@s2;
+------+------+
| @s1 | @s2 |
+------+------+
| 1 | 2 | ##说明以上步骤运行正常
+------+------+
9.2 查看存储过程或函数
查看存储过程和函数的状态的语法格式:
SHOW [PROCEDURE][FUNCTION]STATUS [LIKE'pattern' ];
查看存储过程和函数的定义的语法格式:
SHOW CREATE [PROCEDURE][FUNCTION] sp_name;
mysql> SHOW PROCEDURE STATUS LIKE 'p%'\G
*************************** 1. row ***************************
Db: testdb
Name: p_stat_score
Type: PROCEDURE
Definer: feigu@%
Modified: 2016-11-01 22:02:05
Created: 2016-11-01 22:02:05
Security_type: DEFINER
Comment:
character_set_client: utf8
collation_connection: utf8_general_ci
Database Collation: utf8_general_ci
mysql> SHOW CREATE PROCEDURE p_stat_score\G
*************************** 1. row ***************************
Procedure: p_stat_score
sql_mode:
Create Procedure: CREATE DEFINER=</code>feigu<code>@</code>%<code> PROCEDURE </code>p_stat_score`(IN i_stud_code VARCHAR(20),OUT o_count INT)
BEGIN
SELECT count(*) INTO o_count FROM stud_score WHERE stud_code =i_stud_code;
END
character_set_client: utf8
collation_connection: utf8_general_ci
Database Collation: utf8_general_ci
第10章 数据备份和恢复
10.1 备份数据
备份数据是一项非常重要的事情,是保证数据安全、降低系统损坏、断电、失误操作等等所带来的危害的有力措施。任何的侥幸心理,都可能带来严重后果。
MySQL数据库备份的方法很多,这里我们介绍几种常用的方法:
1)、mysqldump工具
使用mysqldump备份单个数据库中的所有表,其语法格式为:
mysqldump -u user -h host -p dbname>filename.sql
使用mysqldump备份数据库中的部分表,其语法格式为:
mysqldump -u user -h host -p dbname [tablename[,tablename,,,]]>filename.sql
导出的结果包括表结构、数据等信息
2)、使用SELECT ... INTO OUTFILE导出到文件,其命令格式为:
SELECT ... INTO OUTFILE 'path/filename' [参数]
这样导出方式,比较简单,导入也简单,但只导出数据,不包含表结构等信息。
下面通过一个实例来进步说明如何操作,实例的目的是把表stud_info的数据导出到/tmp目录下。
mysql> SELECT COUNT(*) FROM stud_info;
+----------+
| COUNT(*) |
+----------+
| 22 |
+----------+
mysql> SELECT * FROM stud_info into outfile '/tmp/stud_info_20161102.txt'
-> fields terminated by "," enclosed by '"';
Query OK, 22 rows affected (0.00 sec)
验证导出结果:
hadoop@master:/tmp$ ls -l|grep 'stud_info*'
-rw-rw-r-- 1 feigu feigu 1508 Jul 6 15:47 stud_info.csv
hadoop@master:/tmp$ ls -l|grep 'stud_info*' ###文件导出成功
-rw-rw-rw- 1 mysql mysql 2127 Nov 2 09:21 stud_info_20161102.txt
-rw-rw-r-- 1 feigu feigu 1508 Jul 6 15:47 stud_info.csv
hadoop@master:/tmp$ head -3 stud_info_20161102.txt ###查看前3条
"2015101000","王进","M","1997-08-01","2014-09-01","苏州","0000-00-00","10","理学院","1
"2015101001","刘海","M","1997-09-29","2014-09-01","上海","0000-00-00","10","理学院","1
"2015101002","张飞","M","1996-10-21","2014-09-02","济南","0000-00-00","10","理学院","1
hadoop@master:/tmp$ wc -l 22
10.2 恢复数据
恢复数据或还原数据也有多种方法,如通过MySQL命令、工具等。如果备份的文件是以SQL语句的格式保存的可采用执行该文件即可,如source filename.sql,利用工具mysqldump备份出的文件就是sql文件,恢复时就可采用执行文件的方式,其语法格式为:
mysql -u user -h host -p dbname DELETE FROM stud_info; ##全删表数据
Query OK, 22 rows affected (0.08 sec)
mysql> SELECT COUNT(*) FROM stud_info;
+----------+
| COUNT(*) |
+----------+
| 0 |
+----------+
mysql> LOAD DATA INFILE '/tmp/stud_info_20161102.txt' INTO TABLE stud_info
-> fields terminated by "," enclosed by '"' ;
Query OK, 22 rows affected (0.02 sec)
Records: 22 Deleted: 0 Skipped: 0 Warnings: 0
mysql> SELECT COUNT(*) FROM stud_info;
+----------+
| COUNT(*) |
+----------+
| 22 |
+----------+
mysql> SELECT * FROM stud_info LIMIT 2\G
*************************** 1. row ***************************
stud_code: 2015101000
stud_name: 王进
stud_sex: M
birthday: 1997-08-01
log_date: 2014-09-01
orig_addr: 苏州
lev_date: 0000-00-00
college_code: 10
college_name: 理学院
state: 1
*************************** 2. row ***************************
stud_code: 2015101001
stud_name: 刘海
stud_sex: M
birthday: 1997-09-29
log_date: 2014-09-01
orig_addr: 上海
lev_date: 0000-00-00
college_code: 10
college_name: 理学院
state: 1
2 rows in set (0.00 sec)
[/cceN_python]
第11章 性能优化
11.1优化概述
优化数据库是数据库管理人员和开发人员需要具备的一项重要技能,在实际项目中,往往遇到运行一个查询或一个存储过程或显示1张报表耗时十几分钟或几个小时,甚至更多,但经优化后,原来需要几个小时的只要不到一分钟,由此,优化对开发和管理的意义就不言自明了。
数据库的优化,方法很多,但总的原则就是减少系统资源(包括I/O,内存、CPU等)的占有、增强系统的健壮性。
优化的一般步骤:先找到性能瓶颈,然后,根据资源使用情况,找到引起瓶颈的语句或应用,调整结构或设计或参数、优化的过程往往迭代式。
优化的方法主要有设计优化、查询优化、参数的优化等。
11.2优化查询
查询是我们用得最多的操作,提高查询速度是一个我们经常遇到的问题。
如果能及时查询使用资源的情况,将有助于我们发现问题所在,幸好,MySQL提供了一个分析语句:EXPLAIN或DES CRIBE,通过这个分析语句我们可以很方便地看到查询语句查询的行数、是否利用了索引等重要信息。
EXPLAIN语句的基本语法如下:
EXPLAIN 查询语句;

下面对查询结果的各项含义进行说明:
(1)id
Select语句的序列号
(2)select_type
表示查询类型,它主要有如下几种情况:
SIMPLE----表示简单查询,其中不包括连接查询、子查询等;
PRIMARY---表示主查询;
UNION-----表示涉及连接查询
(3)table
表示查询的表
(4)type
表示表的连接类型,各种连接类型从优到差大致有如下几种。
system:该表为仅有一行的系统表
const:数据表最多只有一个匹配行,它查询时开始读取,在后续查询中将优化为常量。const表查询很快,因只需读一次。它一般使用常量值比较主键或唯一索引的所有部分。
如下查询属于这类型:
SELECT * FROM TABLE_NAME WHERE PK_KEY1=a;
eq_ref:从关联表中读取一行,常用于主键或唯一索引字段的等式匹配。
ref: 从关联表中匹配所有行,常用于非主键或唯一索引字段的等式或不等式的匹配。
ref_or_null:。类型如同ref,但多了含null的查询条件;
index_merge:说明连接类型使用了索引合并优化方法;
uique_subquery:使用了索引的子查询
index_subquery:使用了非唯一性索引的子查询
range:搜索指定范围的行
index:只扫描索引
ALL: 进行总表扫描
(5)possible_keys
说明能用哪个索引,如果为null,没有使用索引,可考虑使用或创建相关索引来提高查询效率。
(6)key
茶香中使用到的索引,如果为null,说明没有使用索引。
(7)key_len
指选择索引字段的字节长度,如果为null,则长度为null,通过该值可知道实际使用了组合索引的几个字段。
(8)ref
说明使用了哪列或常数与索引一起查询;
(9)rows
说明查询时查询的行数;
(10)Extra
查询附加信息,如是否用了where等。
通过分析我们知道,该查询是单表查询,是全表扫描,共扫描了118行。
以下介绍通过不同字段查询相同记录的性能分析,看索引对查询的影响。
有一张表存储学生信息的表stud_info,分别通过学院代码字段(建立了一个索引)、学院名称字段(没有索引)查询。
11.3索引对性能的影响
索引对提高查询速度或数据库性能关系非常密切,其效果往往是立竿见影的,如果索引设计合理,能大幅提升的查询效率。下面我们以一个简单实例来说明,比较一个字段在没有索引和有索引的查询效能如何改变。
还是以表stud_info为例,对其字段college_code先没索引到创建索引,然后比较查询性能分析结果。
mysql> SHOW INDEX FROM stud_info \G ###只有一个主键索引
*************************** 1. row ***************************
Table: stud_info
Non_unique: 0
Key_name: PRIMARY
Seq_in_index: 1
Column_name: stud_code
Collation: A
Cardinality: 22
Sub_part: NULL
Packed: NULL
Null:
Index_type: BTREE
Comment:
Index_comment:
1 row in set (0.00 sec)
mysql> EXPLAIN SELECT * FROM stud_info WHERE college_code='10'\G
*************************** 1. row ***************************
id: 1
select_type: SIMPLE
table: stud_info
type: ALL ###全表扫描
possible_keys: NULL
key: NULL
key_len: NULL
ref: NULL
rows: 22
Extra: Using where
1 row in set (0.00 sec)
mysql> ALTER TABLE stud_info ADD INDEX collindex(college_code); ##创建索引
Query OK, 0 rows affected (0.25 sec)
mysql> SHOW INDEX FROM stud_info \G
*************************** 1. row ***************************
Table: stud_info
Non_unique: 0
Key_name: PRIMARY
Seq_in_index: 1
Column_name: stud_code
Collation: A
Cardinality: 22
Sub_part: NULL
Packed: NULL
Null:
Index_type: BTREE
Comment:
Index_comment:
*************************** 2. row ***************************
Table: stud_info
Non_unique: 1
Key_name: collindex ###刚创建的索引
Seq_in_index: 1
Column_name: college_code
Collation: A
Cardinality: 22
Sub_part: NULL
Packed: NULL
Null: YES
Index_type: BTREE
Comment:
Index_comment:
2 rows in set (0.00 sec)
mysql> EXPLAIN SELECT * FROM stud_info WHERE college_code='10'\G ##性能分析
*************************** 1. row ***************************
id: 1
select_type: SIMPLE
table: stud_info
type: ref ##非全表扫描
possible_keys: collindex
key: collindex
key_len: 33
ref: const
rows: 11
Extra: Using where
1 row in set (0.02 sec)
如果有个组合索引,是否创建了索引,然后使用其中一个为查询条件,是否一定走索引呢?我们通过一个实例来看一下,假设我们在stud_score表的stud_code,sub_code两个字段上创建一个联合索引或联合主键。
mysql> DESC stud_score;
+-----------+--------------+------+-----+---------+-------+
| Field | Type | Null | Key | Default | Extra |
+-----------+--------------+------+-----+---------+-------+
| stud_code | varchar(20) | NO | PRI | NULL | |
| sub_code | varchar(20) | NO | PRI | NULL | | ##有联合主键
| sub_name | varchar(100) | YES | | NULL | |
| sub_tech | varchar(20) | YES | | NULL | |
| sub_score | smallint(10) | YES | | NULL | |
| stat_date | date | YES | | NULL | |
+-----------+--------------+------+-----+---------+-------+
6 rows in set (0.01 sec)
mysql> SELECT COUNT(*) FROM stud_score;
+----------+
| COUNT(*) |
+----------+
| 121 |
+----------+
1 row in set (0.06 sec)
mysql> EXPLAIN SELECT * FROM stud_score WHERE sub_code='10104'\G
*************************** 1. row ***************************
id: 1
select_type: SIMPLE
table: stud_score
type: ALL ##说明索引没起作用,还是全表扫描
possible_keys: NULL
key: NULL
key_len: NULL
ref: NULL
rows: 121
Extra: Using where
1 row in set (0.00 sec)
以上例子中虽然我们查询时用到了一个索引字段,但查询时却没有走索引,这是为什么呢?这里违背索引的一条重要原则,即最左原则。该原则是:如果使用的字段不含组合索引中的第一个字段(即最左边那个字段),查询时不走索引。以下我们还是通过实例来验证这个原则。
mysql> EXPLAIN SELECT * FROM stud_score WHERE stud_code='2015101001' and sub_code='10104'\G
*************************** 1. row ***************************
id: 1
select_type: SIMPLE
table: stud_score
type: const
possible_keys: PRIMARY
key: PRIMARY
key_len: 124
ref: const,const
rows: 1
Extra:
1 row in set (0.00 sec)
11.4设计优化
优化工作,除了在查询时需要考虑,实际上在数据库设计或建模时,更应考虑,而且意义更大、影响更广,这是把优化工作前移。一个差的设计方案,不但影响后续优化,甚至影响系统的性能、可靠性、可维护性。
在设计层面考虑优化时,一般主要以下原则:
1、表中字段不宜过多,否则,应考虑大表拆分成几个小表;
2、为减少多表关联,可以考虑适当添加一些冗余字段,或中间表;
3、需要经常出现在where条件的字段,需要考虑建立索引。
4、表分区设计
表分区的定义:
通俗地讲表分区是将一大表,根据条件分割成若干个小表。mysql5.1开始支持数据表分区了。 如:某商品的库存表的记录超过了400万条,那么就可以根据入库日期将表分区,也可以根据所在地将表分区。当然也可根据其他的条件分区。
查看目前MySQL版本是否支持表分区。
mysql> SHOW VARIABLES LIKE '%partition%';
+-------------------+-------+
| Variable_name | Value |
+-------------------+-------+
| have_partitioning | YES |
+-------------------+-------+
1 row in set (0.00 sec)
表分区的意义:
与单个磁盘或文件系统分区相比,可以存储更多的数据。
一些查询可以得到极大的优化,这主要是借助于满足一个给定WHERE语句的数据可以只保存在一个或多个分区内,无需查询所有分区。涉及到例如SUM()和COUNT()这样聚合函数的查询,可以很容易地进行并行处理。
通过跨多个磁盘来分散数据查询,来获得更大的查询吞吐量。
表分区类型:

表分区示例:
mysql> SHOW VARIABLES LIKE '%partition%';
mysql>
DROP TABLE IF EXISTS p_range;
CREATE TABLE p_range (
id int(10) NOT NULL AUTO_INCREMENT,
name char(20) NOT NULL,
PRIMARY KEY (id)
)
PARTITION BY RANGE (id)
(PARTITION p1 VALUES LESS THAN (10),
PARTITION p2 VALUES LESS THAN (20),
PARTITION p3 VALUES LESS THAN MAXVALUE
);
mysql>
DROP TABLE IF EXISTS p_partition;
CREATE TABLE p_partition (
id int(10) DEFAULT NULL,
title char(255) NOT NULL,
createtime date NOT NULL
)
PARTITION BY RANGE (YEAR(createtime))
(PARTITION p0 VALUES LESS THAN (2012),
PARTITION p1 VALUES LESS THAN (2013),
PARTITION p2 VALUES LESS THAN MAXVALUE
);
mysql>
DROP TABLE IF EXISTS p_list;
CREATE TABLE p_list (
id int(10) NOT NULL AUTO_INCREMENT,
typeid mediumint(10) NOT NULL DEFAULT '0',
typename char(20) DEFAULT NULL,
PRIMARY KEY (id,typeid)
)
PARTITION BY LIST (typeid)
(PARTITION p0 VALUES IN (1,2,3,4),
PARTITION p1 VALUES IN (5,6,7,8));
mysql>
DROP TABLE IF EXISTS p_hash;
CREATE TABLE p_hash (
id int(10) NOT NULL AUTO_INCREMENT,
storeid mediumint(10) NOT NULL DEFAULT '0',
storename char(255) DEFAULT NULL,
PRIMARY KEY (id,storeid)
) PARTITION BY HASH (storeid)
PARTITIONS 4 ;
mysql>
explain partitions select * from p_hash
11.5系统优化
数据库系统方面的优化,主要涉及系统资源的优化、架构的优化及一些系统参数的优化。
系统资源方面的优化主要有以下方法:
1、配上较大的内存、或使用集群方式,共享内存,可大大增加内存总量;
2、配置高速磁盘系统,或采用集群方式,便于把数据分布到不同节点上。
3、采用多线程的处理器,或采用集群方式,提升并发处理能力。
在系统参数方面,需要关注以下参数:
1、max_connections:表示数据库的最大连接数。
2、query_cache_size:表示查询缓存大小。
3、sort_buffer_size:用来排序的缓冲大小。
4、key_buffer_size:表示索引缓存大小。
(注:参数涉及配置文件my.cnf)
附录1:常见问题
一、连接数据库丢失SOCK
在MySQL服务器上连接数据库时,有时报can't connect to /tmp/mysql.sock类似错误。
这是因为连接中指定的localhost作为一个主机名,而mysqladmin默认使用Unix套接字文件(一命名为mysql.SOCK),而不是TCP/IP。为此,解决此类问题,
1、显式说明指明连接协议,如mysql --protocol=TCP -u user -p -h localhost
2、可以把localhost改为127.0.0.1
3、在连接信息中添加文件mysql.sock所在位置,这个参数(如unix_socket="/var/run/mysqld/mysqld.sock"),
4、修改相关配置参数my.cnf中socket。修改配置文件需要停启服务。
二、中文乱码问题
中文乱码一般是数据库(或表)字符集与客户端字符集、应用字符集不兼容导致的,三者间如果其中两个不兼容就有可能导致乱码。
查看表的字符集:mysql>SHOW CREATE TALE tablename;
查看文件的字符集:vim或vi 文件名,然后输入:set fileencoding 可以查看文件字符集
查看服务、数据库、客户端等字符集:
mysql>show variables like '%char%';
修改客户端字符集:mysql>SET character_set_results=字符集(utf8,gbk等);
三、mysql导入csv报错ERROR 29 (HY000): File not found (Errcode: 13)
解决方法;
1、在mysqld中添加存放数据路径的读写权限
假设存放数据路径为/tmp
#vi /etc/apparmor.d/usr.sbin.mysqld
在最后添加以下两行
/tmp/ r,
/tmp/* rw,
2、然后重新加载这个文件
#/etc/init.d/apparmor reload
附录2:课后练习
一、在windows下安装配置MySQL,并尝试在cmd启动并连接mysql。
二、在testdb库上创建表,表结构如下:
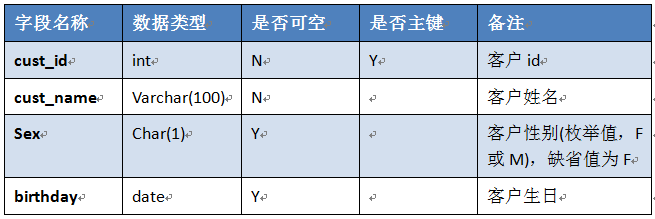
写一个sql文件,功能包括:
1、创建以上表结构,表名为:test_学号;
2、往表test_序号插入至少3条数据;
3、在表最后位置添加一个字段,字段要求如下:

三、创建表并把数据导入表中,然后查询相关数据,把这些操作放到一个SQL文件中,具体要求如下:
1、创建两表,表名分别为,stud_score_学号:stud_info_学号,表结构请参考第6.2.1节和6.3.1节
2、导入数据,把/tmp目录下stud_info.csv,stud_score.csv分别导入到表stud_info_学号,stud_score_学号中
3、查询数据,查询表stud_info_学号中,把姓刘的同学过滤出来。
四、多表查询,在一个SQL语句实现以下功能
1、内连接,实现stud_score_学号:stud_info_学号的内连接,连接字段为stud_code
2、左连接, 实现stud_score_学号:stud_info_学号的左连接,连接字段为stud_code
五、聚合查询
1、把选了大于5门课的同学的名称及各科总成绩打印出来。
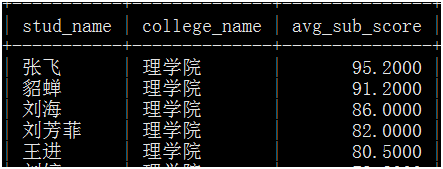
六、写一个存储过程,实现功能,输入学院代码,输出,学生名称、学院名称、各科平均成绩,如下图:
七、备份数据
1、导出表stud_socre_学号的数据,并验证导出数据的总条数、是否有乱码等。
八、性能优化
1、谈谈你对数据库优化方法,可包括数据库设计、SQL编写等方面内容。
此外大家还可参考网站其他数据库经典博客或文章 或My SQL 基础入门 或MySQL入门200句

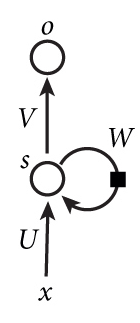


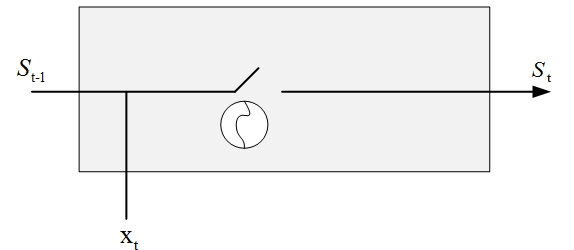



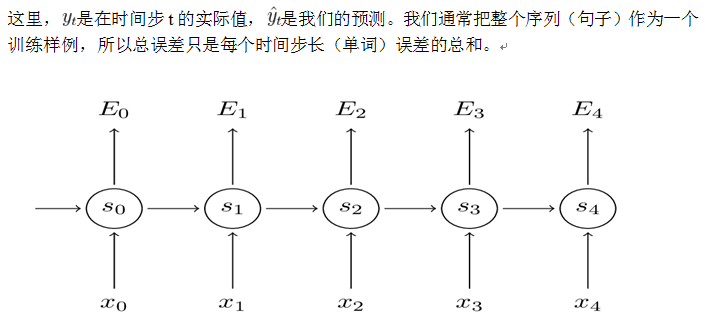
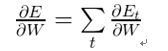


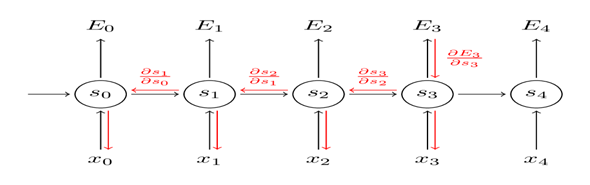
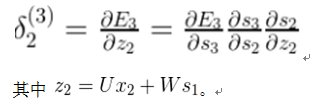

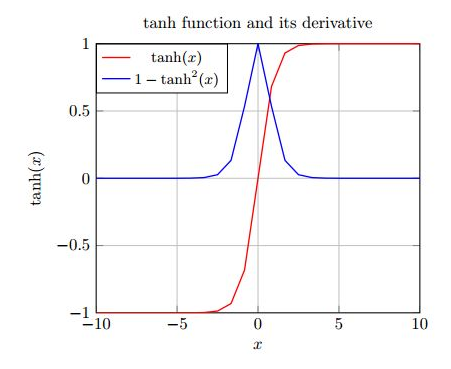
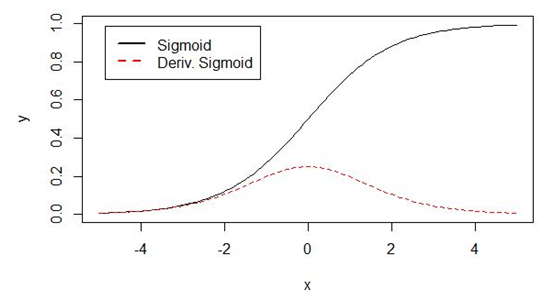



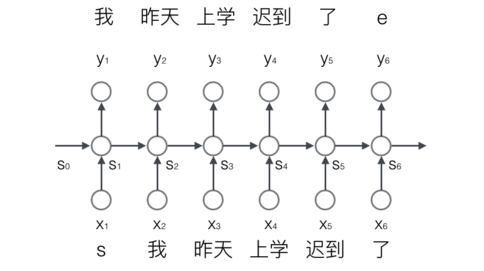


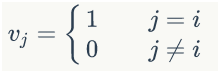
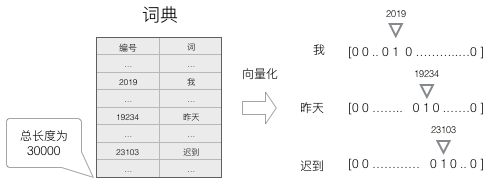
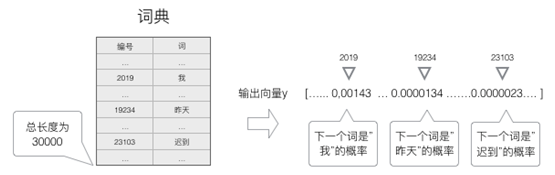
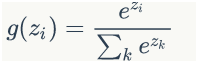


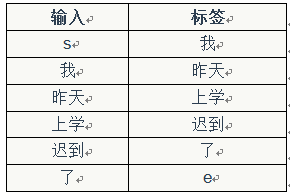
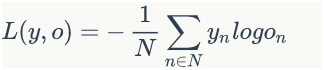


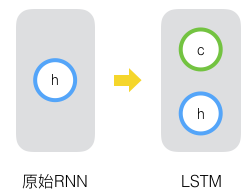


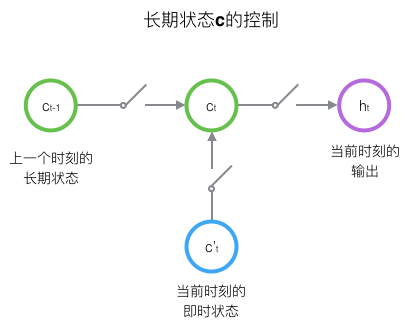
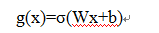
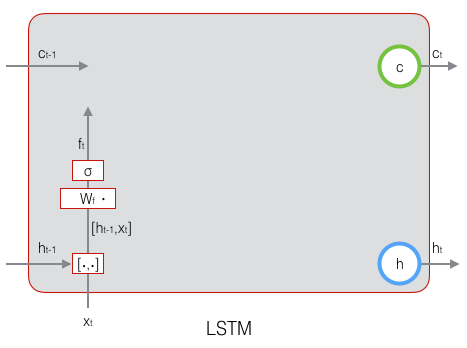
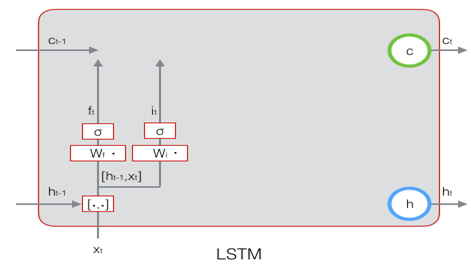
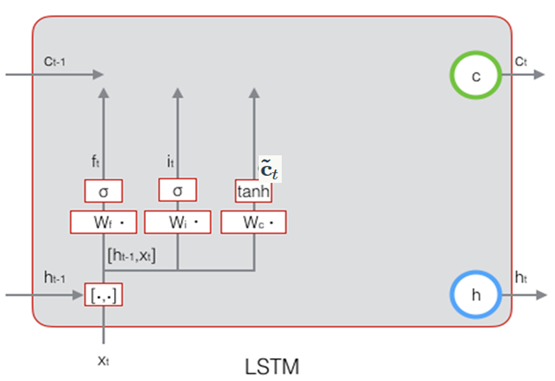
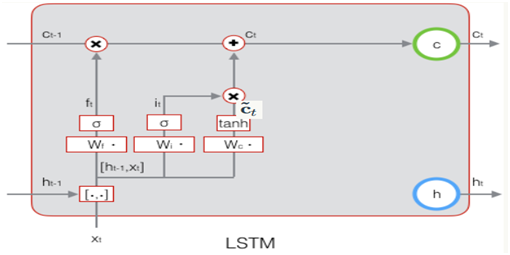
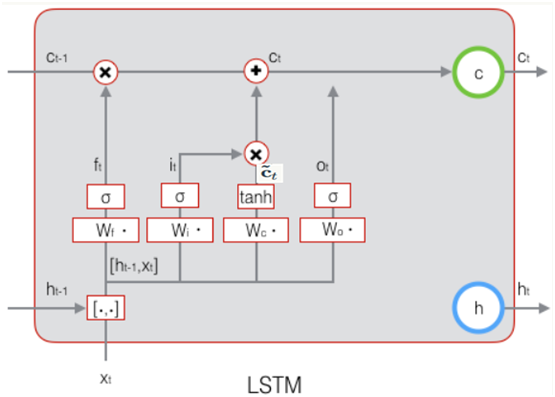
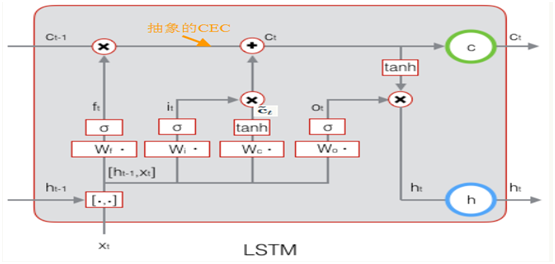
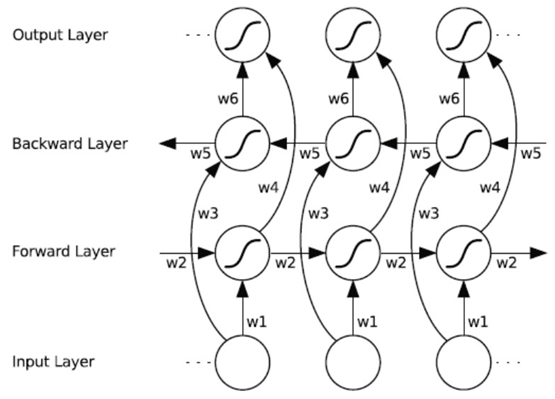
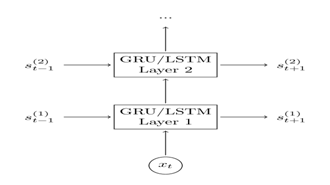
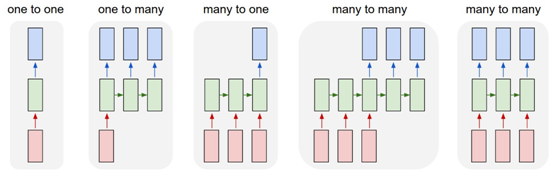
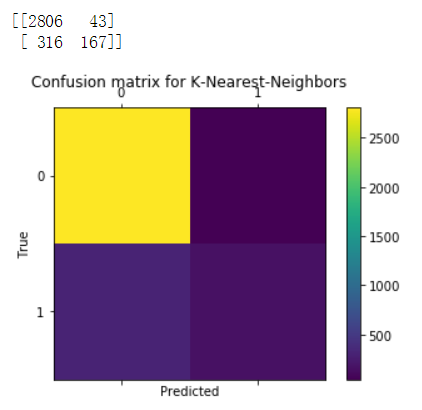
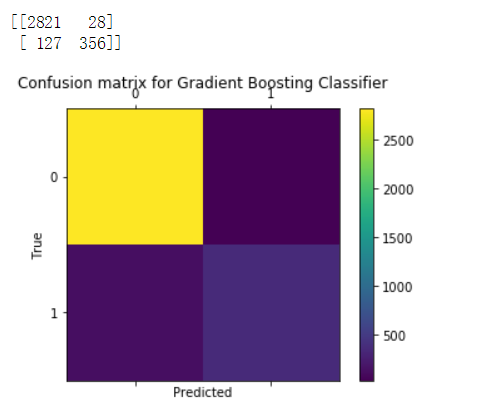
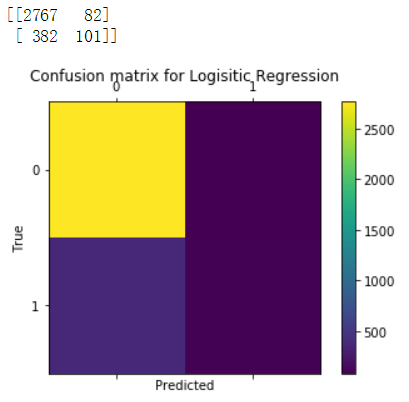
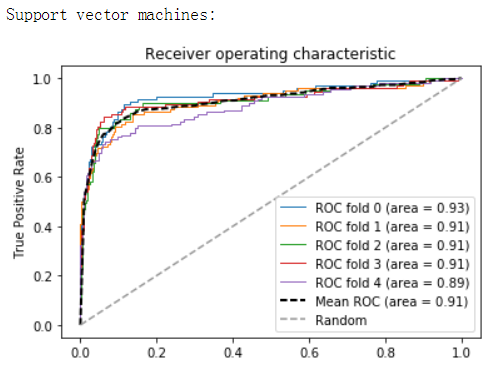
 下图显示了遗忘门的计算过程:
下图显示了遗忘门的计算过程:








































 倍的数据量。如果没有数据增强,仅靠原始的数据量,参数众多的CNN会陷入过拟合中,使用了数据增强后可以大大减轻过拟合,提升泛化能力。进行预测时,则是取图片的四个角加中间共5个位置,并进行左右翻转,一共获得10张图片,对他们进行预测并对10次结果求均值。同时,AlexNet论文中提到了会对图像的RGB数据进行PCA处理,并对主成分做一个标准差为0.1的高斯扰动,增加一些噪声,这个Trick可以让错误率再下降1%。
倍的数据量。如果没有数据增强,仅靠原始的数据量,参数众多的CNN会陷入过拟合中,使用了数据增强后可以大大减轻过拟合,提升泛化能力。进行预测时,则是取图片的四个角加中间共5个位置,并进行左右翻转,一共获得10张图片,对他们进行预测并对10次结果求均值。同时,AlexNet论文中提到了会对图像的RGB数据进行PCA处理,并对主成分做一个标准差为0.1的高斯扰动,增加一些噪声,这个Trick可以让错误率再下降1%。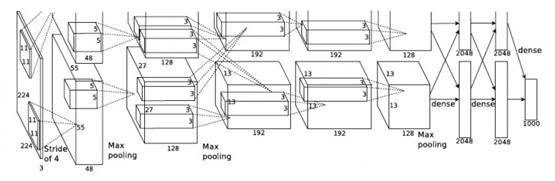















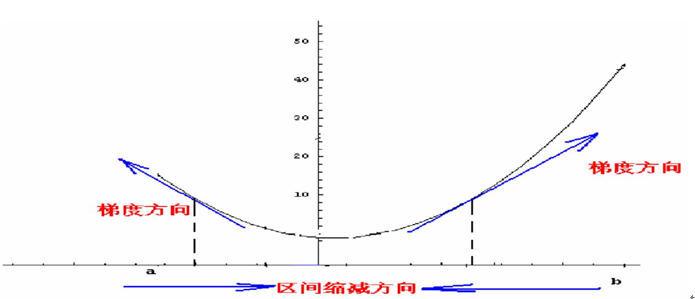

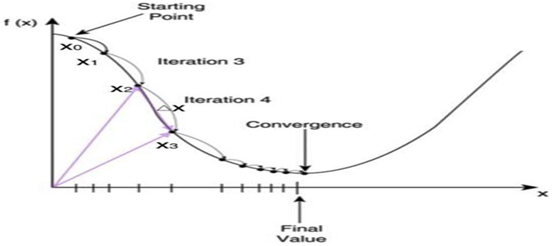

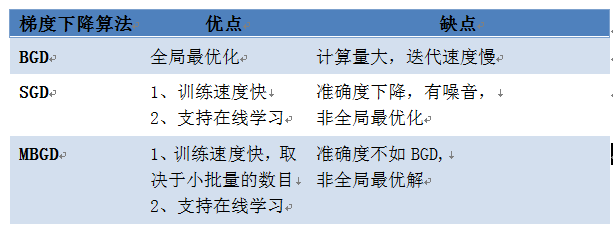
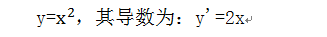


 为例,这次引入衰减因子decay 来改变学习速率。
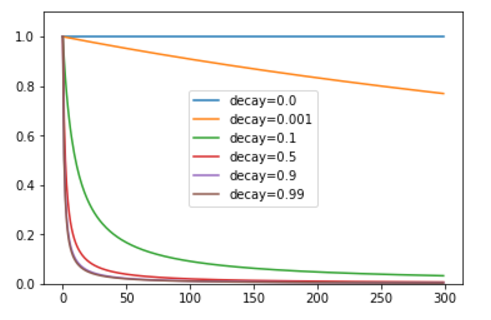
为例,这次引入衰减因子decay 来改变学习速率。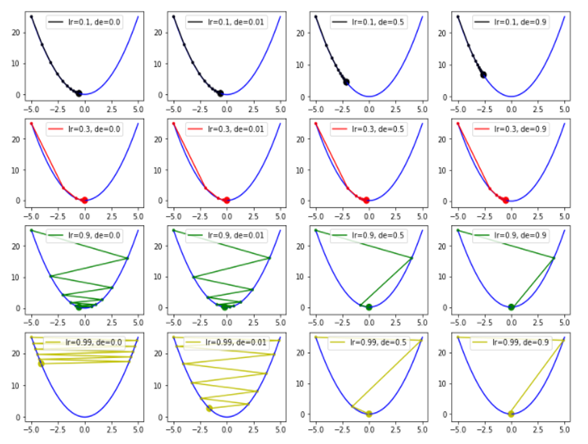

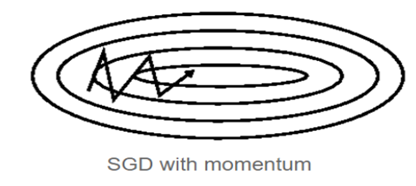

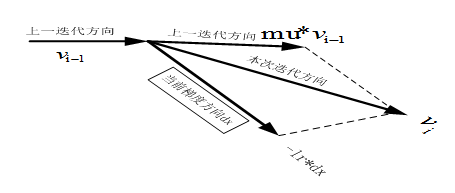
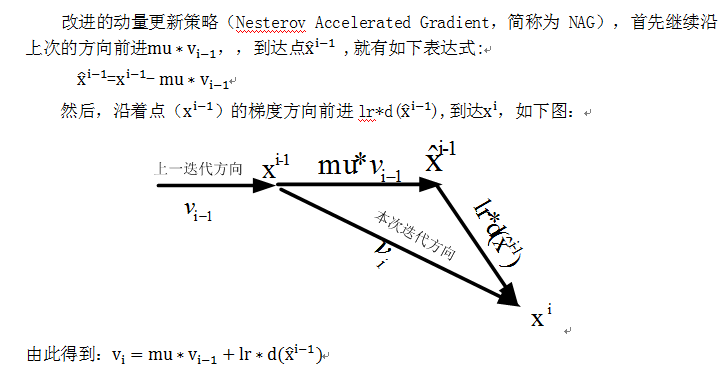
 的方向相同时,上次的更新量能够对本次的搜索起到一个正向加速的作用。
的方向相同时,上次的更新量能够对本次的搜索起到一个正向加速的作用。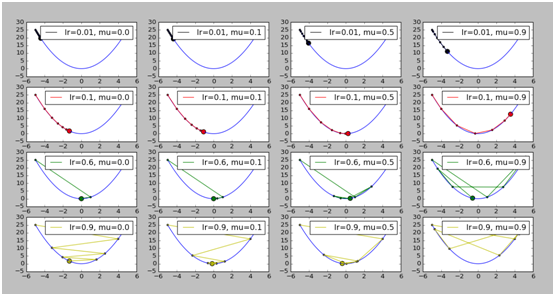
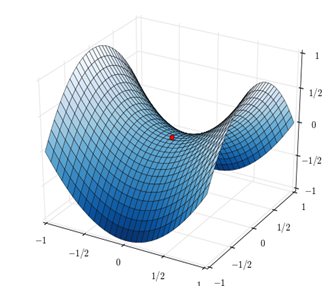
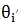 使用相同的学习速率η,而Adagrad在每一个更新步骤中对于每一个模型参数
使用相同的学习速率η,而Adagrad在每一个更新步骤中对于每一个模型参数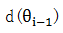 ,
,
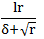 随着时间就减小,在接近目标值时,不会因为学习速率过大而越过极值点;
随着时间就减小,在接近目标值时,不会因为学习速率过大而越过极值点;


































 ,
,
























 。
。























 Vladimir Vapnik
Vladimir Vapnik