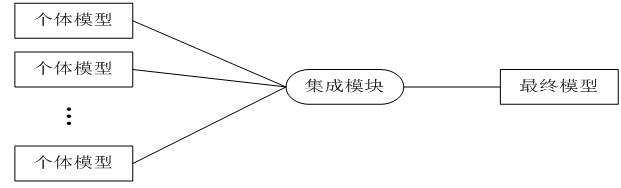
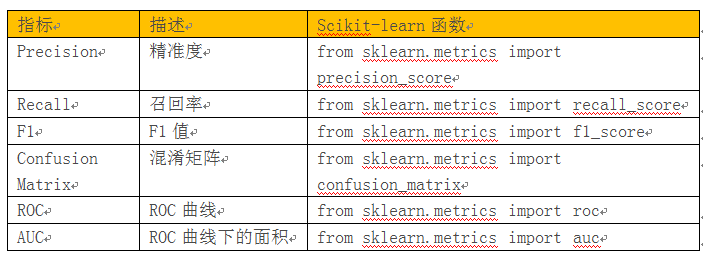
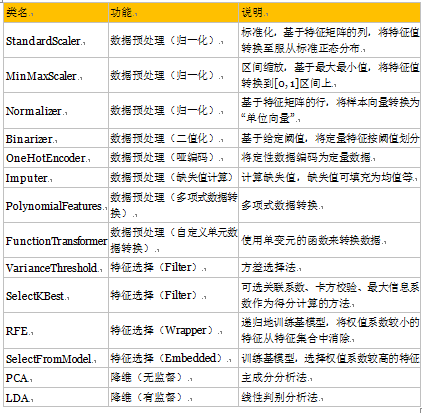
1、整体思路:
理解问题:查看每个变量并且根据他们的意义和对问题的重要性进行哲学分析。
单因素研究:只关注因变量(‘SalePrice’),并且进行更深入的了解。
多因素研究:分析因变量和自变量之间的关系。、
基础清洗:清洗数据集并且对缺失数据,异常值和分类数据进行一些处理。
检验假设:检查数据是否和多元分析方法的假设达到一致。
开始之前,先导入需要的库及文件:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from scipy.stats import norm
from sklearn.preprocessing import StandardScaler
from scipy import stats
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
#bring in the six packs
df_train = pd.read_csv('./data/house_train.csv')
查看特征
df_train.columns
Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street', 'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig','LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType','HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd','RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType','MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual','BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1','BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating','HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF','LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath','HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual','TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType','GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual','GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF','EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC','Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType','SaleCondition', 'SalePrice'], dtype='object')
2、准备工作
为了了解我们的数据,我们可以分析每个变量并且尝试理解他们的意义和与该问题的相关程度。
首先建立一个 Excel 电子表格,有如下目录:
变量 – 变量名。
类型 – 该变量的类型。这一栏只有两个可能值,“数据” 或 “类别”。 “数据” 是指该变量的值是数字,“类别” 指该变量的值是类别标签。
划分 – 指示变量划分. 我们定义了三种划分:建筑,空间,位置。
期望 – 我们希望该变量对房价的影响程度。我们使用类别标签 “高”,“中” 和 “低” 作为可能值。
结论 – 我们得出的该变量的重要性的结论。在大概浏览数据之后,我们认为这一栏和 “期望” 的值基本一致。
评论 – 我们看到的所有一般性评论。
我们首先阅读了每一个变量的描述文件,同时思考这三个问题:
我们买房子的时候会考虑这个因素吗?
如果考虑的话,这个因素的重要程度如何?
这个因素带来的信息在其他因素中出现过吗?
我们根据以上内容填好了电子表格,并且仔细观察了 “高期望” 的变量。然后绘制了这些变量和房价之间的散点图,填在了 “结论” 那一栏,也正巧就是对我们的期望值的校正。
我们总结出了四个对该问题起到至关重要的作用的变量:
OverallQual
YearBuilt.
TotalBsmtSF.
GrLivArea.
最重要的事情——分析 “房价”
df_train['SalePrice'].describe()
count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000
Name: SalePrice, dtype: float64
绘制直方图
sns.distplot(df_train['SalePrice']);

用seaborn绘图,得出结论:
-偏离正态分布
-数据正偏
-有峰值
数据偏度和峰度度量:
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())
Skewness: 1.882876
Kurtosis: 6.536282
偏度(Skewness)是描述某变量取值分布对称性的统计量。如果偏度=0,和正态分布的偏度相同;Skewness>0,长尾巴拖在右边;Skewness<0,长尾巴拖在左边,Skewness越大,分布形态偏移程度越大。 峰度(Kurtosis)是描述某变量所有取值分布形态陡缓程度的统计量。它是和正态分布相比较的:Kurtosis=0,与正态分布的陡缓程度相同;Kurtosis>0,比正态分布的高峰更加陡峭;反之亦然。
3、与数值类型的关系
(1)grlivarea/saleprice的散点图绘制
首先观察一下saleprice和数值型变量grlivarea之间的关系。我们还是可以观察到整体的趋势的,随着grlivarea的增大,saleprice有变高的趋势。存在线性关系!
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
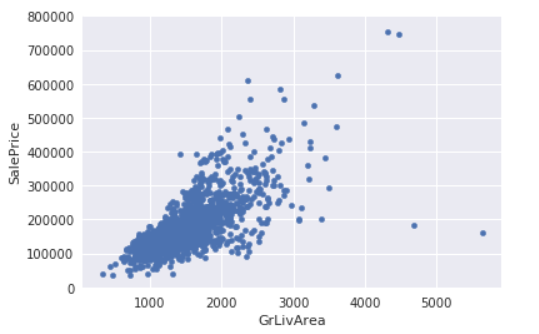
可以看出’’SalePrice’和’'GrLivArea' 关系很密切,并且基本呈线性关系。
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
TotalBsmtSF' 和 'SalePrice'关系也很密切,从图中可以看出基本呈指数分布,但从最左侧的点可以看出特定情况下’TotalBsmtSF' 对'SalePrice' 没有产生影响。
4、与类别类型的关系
(1)overallqual/saleprice的箱形图
这里有一个问题,为什么我们不用散点图了呢?那么先画一个散点图看下效果。如下图:
#box plot overallqual/saleprice
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);

可见也是有相互关系的,如果用箱形图表示的话,会更加清晰:
(2)YearBuilt/saleprice的箱形图
两个变量之间的关系没有很强的趋势性,但是可以看出建筑时间较短的房屋价格更高。
var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y="SalePrice", data=data)
fig.axis(ymin=0, ymax=800000);
plt.xticks(rotation=90);

两个变量之间的关系没有很强的趋势性,但是可以看出建筑时间较短的房屋价格更高。
总结:
'GrLivArea' 和 'TotalBsmtSF' 与 'SalePrice'似乎线性相关,并且都是正相关。 对于 'TotalBsmtSF',线性关系的斜率十分的高。
'OverallQual' 和 'YearBuilt' 与 'SalePrice'也有关系。'OverallQual'的相关性更强, 箱型图显示了随着整体质量的增长,房价的增长趋势。
我们只分析了四个变量,但是还有许多其他变量我们也应该分析,这里的技巧在于选择正确的特征(特征选择)而不是定义他们之间的复杂关系(特征工程)。它们之间的复杂关系可以通过模型学习。
5、客观分析
上面的分析过于主观,我们应该更客观的去分析。
主要有三方面的分析:
-相关矩阵热图
-SalePrice相关矩阵热图
-最相关变量之间的散点图
(1)相关矩阵热图
#correlation matrix
corrmat = df_train.corr()
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
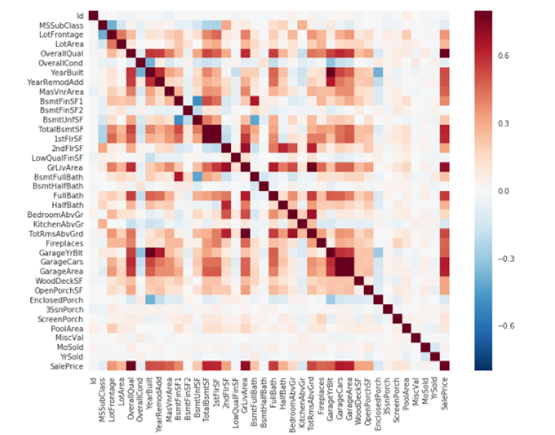
热图是观察特征和特征、特征和label之间关系的一种快速的方式。首先,最吸引注意的是两个红色方块。第一处指向TotalBsmtSF和1stFlrSF这两个变量,第二处指向Garage相关的变量。这两块显示了TotalBsmtSF和1stFlrSF的相关性、GarageCar和GarageArea的相关性很大。事实上,这种关联性很强,暗示它们存在多重共线性。我们能够推断当变量间具有多重共线性,那么它们给出的信息也基本上是一样的。Heatmaps恰恰可以检测多重共线性的情况并决定选择哪些特征,所以是一个非常重要的工具。
另外观察特征和SalePrice之间的关系,可以看到GrLivArea、TotalBsmtSF、OverallQual,也看到了一些其他的变量应该纳入我们考虑。
(2)SalePrice相关矩阵热图
筛选与SalePrice相关性强的特征,重点观察。
#saleprice correlation matrix
k = 10 #number of variables for heatmap
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index
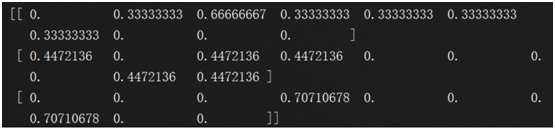
cm = np.corrcoef(df_train[cols].values.T)
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 10}, yticklabels=cols.values, xticklabels=cols.values)
plt.show()
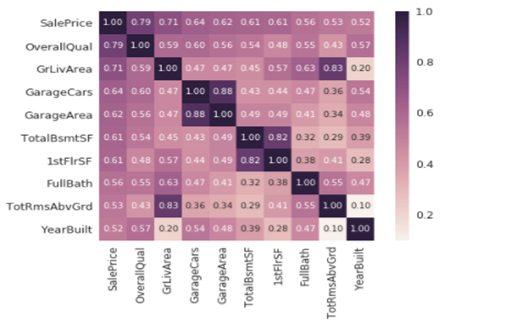
从图中可以看出:
'OverallQual', 'GrLivArea' 以及 'TotalBsmtSF' 与 'SalePrice'有很强的相关性。
'GarageCars' 和 'GarageArea' 也是相关性比较强的变量. 车库中存储的车的数量是由车库的面积决定的,它们就像双胞胎,所以不需要专门区分'GarageCars' 和 'GarageArea' ,所以我们只需要其中的一个变量。这里我们选择了'GarageCars'因为它与'SalePrice' 的相关性更高一些。
'TotalBsmtSF' 和 '1stFloor' 与上述情况相同,我们选择 'TotalBsmtSF' 。
'FullBath'几乎不需要考虑。
'TotRmsAbvGrd' 和 'GrLivArea'也是变量中的双胞胎。
'YearBuilt' 和 'SalePrice'相关性似乎不强。
(3).'SalePrice' 和相关变量之间的散点图
#scatterplot
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF', 'FullBath', 'YearBuilt']
sns.pairplot(df_train[cols], size = 2.5)
plt.show();
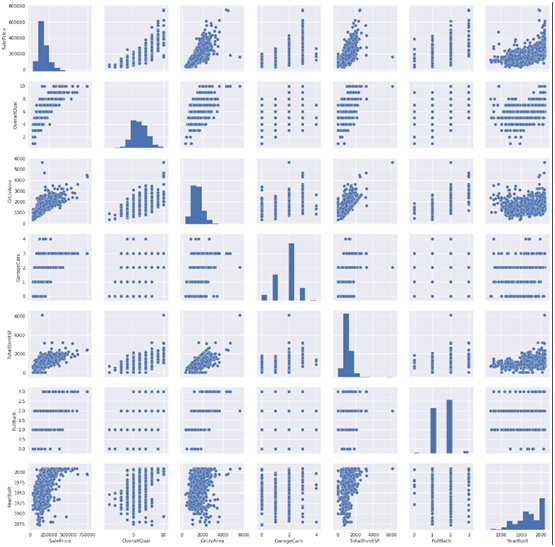
尽管我们已经知道了一些主要特征,这一丰富的散点图给了我们一个关于变量关系的合理想法。其中,'TotalBsmtSF' 和 'GrLiveArea'之间的散点图是很有意思的。我们可以看出这幅图中,一些点组成了线,就像边界一样。大部分点都分布在那条线下面,这也是可以解释的。地下室面积和地上居住面积可以相等,但是一般情况下不会希望有一个比地上居住面积还大的地下室。
'SalePrice' 和'YearBuilt' 之间的散点图也值得我们思考。在“点云”的底部,我们可以观察到一个几乎呈指数函数的分布。我们也可以看到“点云”的上端也基本呈同样的分布趋势。并且可以注意到,近几年的点有超过这个上端的趋势。
6、缺失数据
关于缺失数据需要思考的重要问题:
这一缺失数据的普遍性如何?
缺失数据是随机的还是有律可循?
这些问题的答案是很重要的,因为缺失数据意味着样本大小的缩减,这会阻止我们的分析进程。除此之外,以实质性的角度来说,我们需要保证对缺失数据的处理不会出现偏离或隐藏任何难以忽视的真相。
#missing data
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
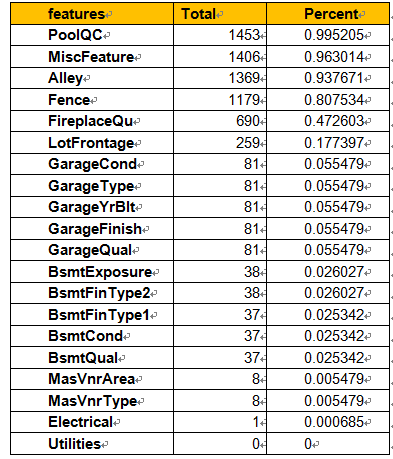
(1)当超过15%的数据都缺失的时候,我们应该删掉相关变量且假设该变量并不存在。根据这一条,一系列变量都应该删掉,例如'PoolQC', 'MiscFeature', 'Alley'等等,这些变量都不是很重要,因为他们基本都不是我们买房子时会考虑的因素。
(2)'GarageX' 变量群的缺失数据量都相同,由于关于车库的最重要的信息都可以由'GarageCars' 表达,并且这些数据只占缺失数据的5%,我们也会删除上述的'GarageX' 变量群。同样的逻辑也适用于 'BsmtX' 变量群。
(3)对于 'MasVnrArea' 和 'MasVnrType',我们可以认为这些因素并不重要。除此之外,他们和'YearBuilt' 以及 'OverallQual'都有很强的关联性,而这两个变量我们已经考虑过了。所以删除 'MasVnrArea'和 'MasVnrType'并不会丢失信息。
(4)最后,由于'Electrical'中只有一个损失的观察值,所以我们删除这个观察值,但是保留这一变量。
#dealing with missing data
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index,1)
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index)
df_train.isnull().sum().max() #just checking that there's no missing data missing...
总结:处理空值,我们删掉所有有较多空值的特征,除了特征Electrical,因为只有一个缺失值,所以删除含该空值的样本即可。
7、异常值处理
异常值也是我们应该注意的东西。因为异常值能明显的影响我们的模型,并且是一个有价值的信息来源,帮助我们对特定行为有更多的见解。异常值是一个复杂的主题,并且值得研究。在这里,我们将用SalePrice的标准差和一系列的散点来进行快速分析。
7.1单因素分析
这里的关键在于如何建立阈值,定义一个观察值为异常值。
我们对数据进行正态化,意味着把数据值转换成均值为0,方差为1的数据。
#standardizing data
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'][:,np.newaxis]);
low_range = saleprice_scaled[saleprice_scaled[:,0].argsort()][:10]
high_range= saleprice_scaled[saleprice_scaled[:,0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)
outer range (low) of the distribution:
[[-1.83820775]
[-1.83303414]
[-1.80044422]
[-1.78282123]
[-1.77400974]
[-1.62295562]
[-1.6166617 ]
[-1.58519209]
[-1.58519209]
[-1.57269236]]
outer range (high) of the distribution:
[[ 3.82758058]
[ 4.0395221 ]
[ 4.49473628]
[ 4.70872962]
[ 4.728631 ]
[ 5.06034585]
[ 5.42191907]
[ 5.58987866]
[ 7.10041987]
[ 7.22629831]]
进行正态化后,可以看出:
低范围的值都比较相似并且在0附近分布。
高范围的值离0很远,并且7点几的值远在正常范围之外。
现在看,我们不把任何值作为异常值,但是我们应该注意这两个大于7的值。
7.2双变量分析
#bivariate analysis saleprice/grlivarea
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
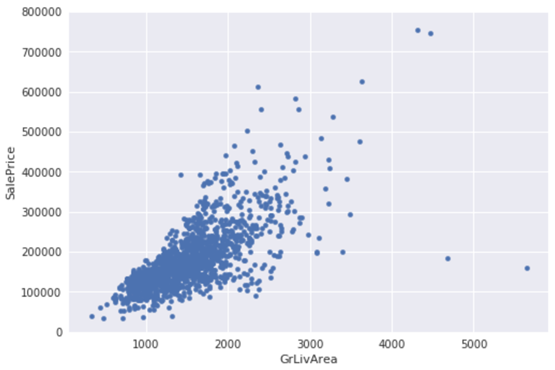
这是之前GrLivArea和SalePrice关系散点图:
(1)有两个离群的'GrLivArea' 值很高的数据,我们可以推测出现这种情况的原因。或许他们代表了农业地区,也就解释了低价。 这两个点很明显不能代表典型样例,所以我们将它们定义为异常值并删除。
(2)图中顶部的两个点是七点几的观测值,他们虽然看起来像特殊情况,但是他们依然符合整体趋势,所以我们将其保留下来。
删除异常点:
df_train.sort_values(by = 'GrLivArea', ascending = False)[:2]
df_train = df_train.drop(df_train[df_train['Id'] == 1299].index)
df_train = df_train.drop(df_train[df_train['Id'] == 524].index)
(3). 'TotalBsmtSF'和'SalePrice'双变量分析
#bivariate analysis saleprice/grlivarea
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0,800000));
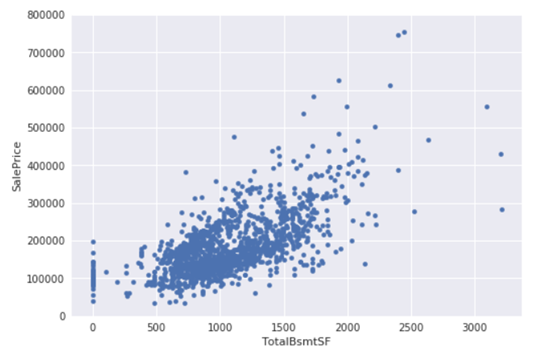
我们可以感觉到试图消除一些观察(例如,TotalBsmtSF> 3000),但是我们认为这是不值得的。 我们可以保留它们,所以我们不会做任何事情。
8、核心部分
核心部分
“房价”到底是谁?
这个问题的答案,需要我们验证根据数据基础进行多元分析的假设。
我们已经进行了数据清洗,并且发现了“SalePrice”的很多信息,现在我们要更进一步理解‘SalePrice’如何遵循统计假设,可以让我们应用多元技术。
应该测量4个假设量:
(1)正态性:它的重要在于很多统计检验是基于正态分布的,在房价预测的问题中,我们只检查了单变量的正态性。但是单变量正态性不能确保多变量的正态性,但是会其帮助作用。
(2)同方差性:假设在预测变量的范围因变量表现出同等水平的方差
(3)线性:通过观察散点图,看是否为线性关系,如果不是,需要数据转换,但是大多数情况下都是满足线性关系的。
(4)相关错误缺失
1). ‘SalePrice’
正态性:
应主要关注以下两点:
直方图 - 峰度和偏度。
正态概率图 - 数据分布应紧密跟随代表正态分布的对角线。
#histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

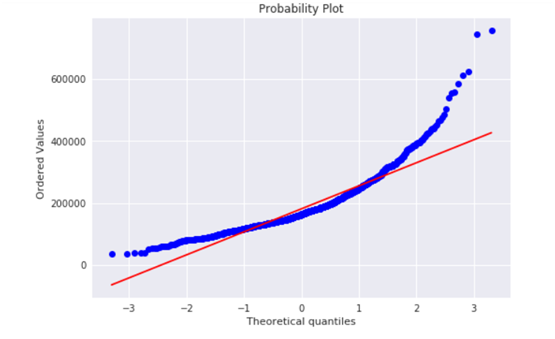
可以看出,房价分布不是正态的,显示了峰值,正偏度。但是,信息没有丢失,简单的数据变换就可以解决这个问题,为了防止正偏,log变换作用很好。
#applying log transformation
df_train['SalePrice'] = np.log(df_train['SalePrice'])
#transformed histogram and normal probability plot
sns.distplot(df_train['SalePrice'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
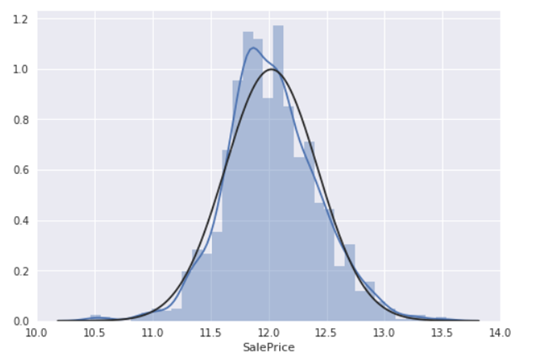

从图中可以看出:
显示出了偏度
大量为0的观察值(没有地下室的房屋)
含0的数据无法进行对数变换,可用log(x+1)
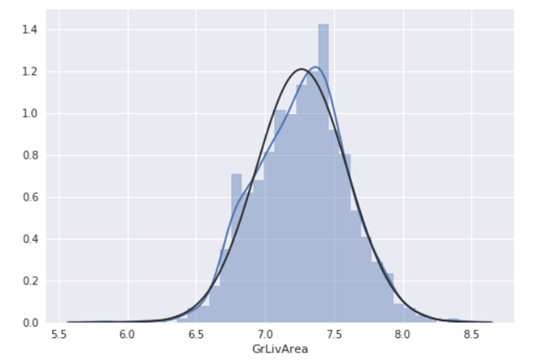
2). GrLivArea
绘制直方图和正态概率曲线图:
#histogram and normal probability plot
sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)
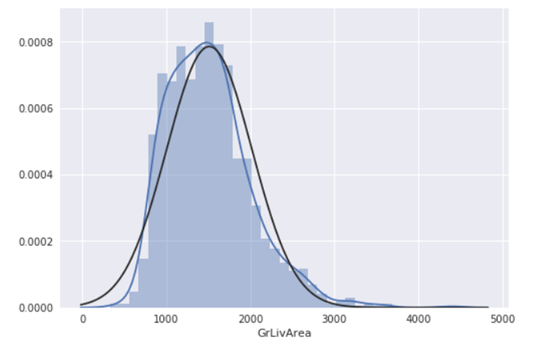
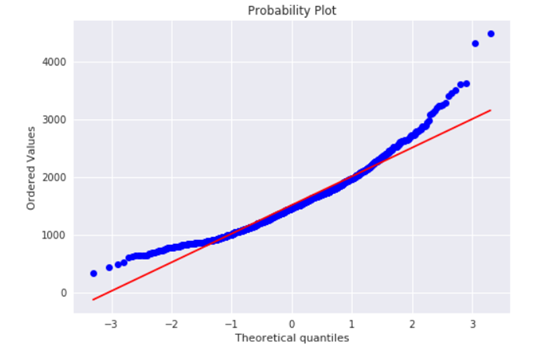
进行对数变换:
#data transformation
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])
#transformed histogram and normal probability plot
sns.distplot(df_train['GrLivArea'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

3). 'TotalBsmtSF'
绘制直方图和正态概率曲线图:
#histogram and normal probability plot
sns.distplot(df_train['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)
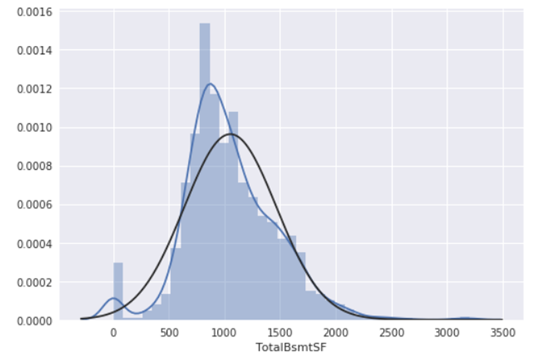
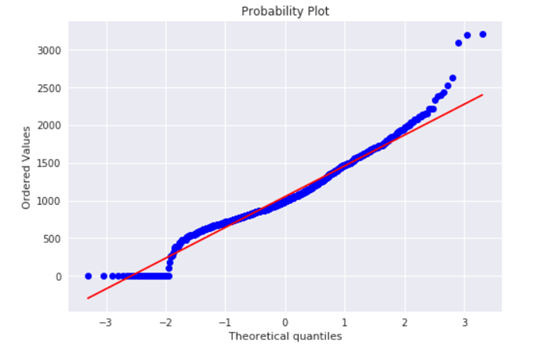
从图中可以看出:
显示出了偏度
大量为 0 的观察值(没有地下室的房屋)
含 0 的数据无法进行对数变换
我们建立了一个变量,可以得到有没有地下室的影响值(二值变量),我们选择忽略零值,只对非零值进行对数变换。这样我们既可以变换数据,也不会损失有没有地下室的影响。
#create column for new variable (one is enough because it's a binary categorical feature)
#if area>0 it gets 1, for area==0 it gets 0
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0
df_train.loc[df_train['TotalBsmtSF']>0,'HasBsmt'] = 1
对该变量进行转换
#transform data
df_train.loc[df_train['HasBsmt']==1,'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])
#histogram and normal probability plot
sns.distplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], fit=norm);
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], plot=plt)
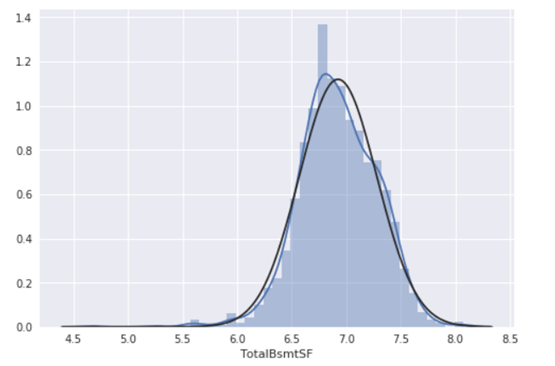

9、同方差性
最好的测量两个变量的同方差性的方法就是图像。
1). SalePrice 和 GrLivArea 同方差性
绘制散点图:
#scatter plot
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);

2).'SalePrice' with 'TotalBsmtSF'同方差性
绘制散点图:
#scatter plot
plt.scatter(df_train[df_train['TotalBsmtSF']>0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF']>0]['SalePrice']);

可以看出'SalePrice'在整个 'TotalBsmtSF'变量范围内显示出了同等级别的变化。
这就是正态化的作用,我们仅仅需要保证特征的正态化,就能解决同方差的问题。
10、虚拟变量
对类别变量进行虚拟编码:
df_train['SaleCondition'].unique()
array(['Normal', 'Abnorml', 'Partial', 'AdjLand', 'Alloca', 'Family'], dtype=object)
#convert categorical variable into dummy
df_train = pd.get_dummies(df_train)
df_train
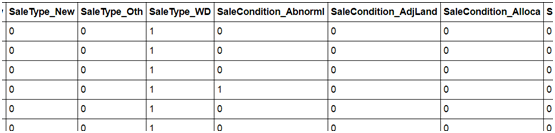
1457 rows × 222 columns
[/cceN_python]
结论
整个方案中,我们使用了很多《多元数据分析》中提出的方法。我们对变量进行了哲学分析,不仅对'SalePrice'进行了单独分析,还结合了相关程度最高的变量进行分析。我们处理了缺失数据和异常值,我们验证了一些基础统计假设,并且将类别变量转换为虚拟变量。
但问题还没有结束,我们还需要预测房价的变化趋势,房价预测是否适合线性回归正则化的方法?是否适合组合方法?或者一些其他的方法?这篇文章解决了数据预处理的问题,预处理后,我们选择正确的模型算法进行拟合。
参考以下网站:
http://www.jianshu.com/p/defcbbfdb324

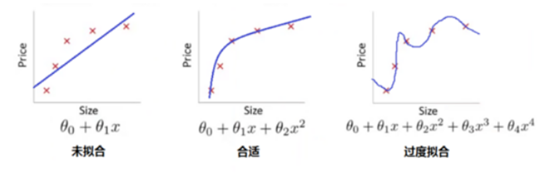

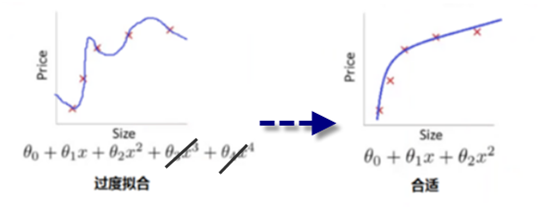
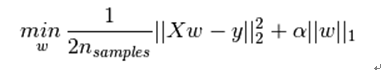
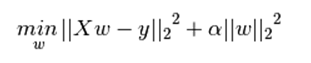
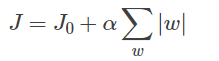

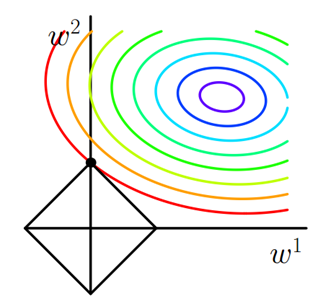

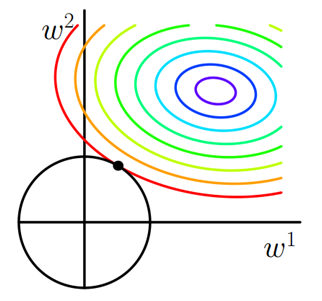








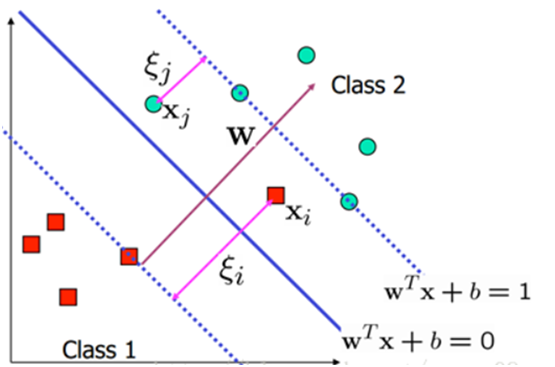


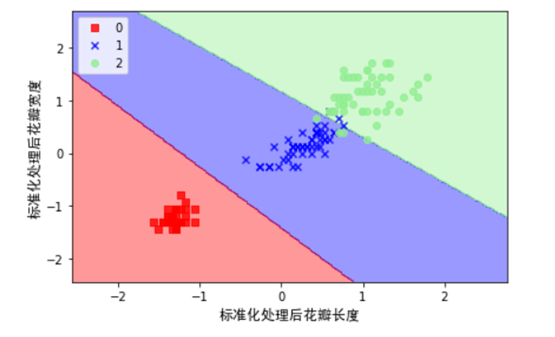
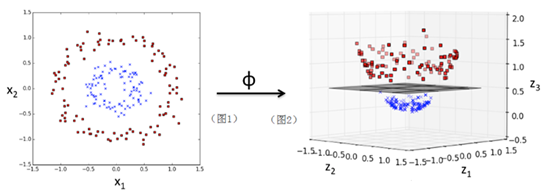
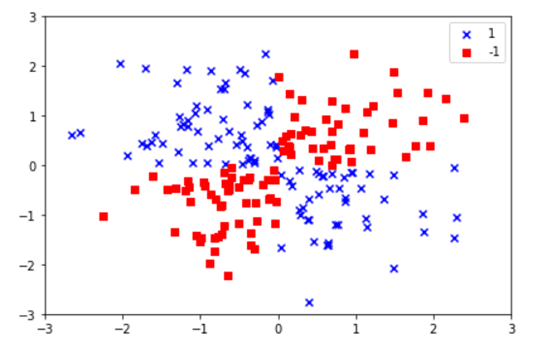


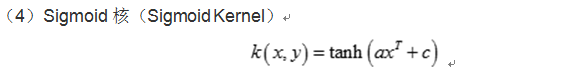
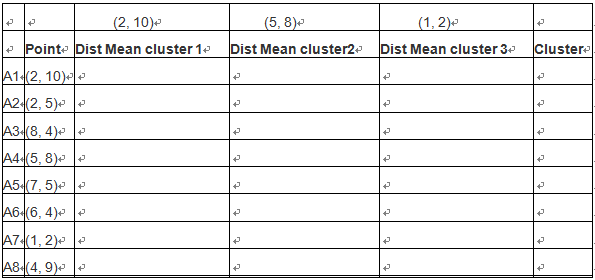
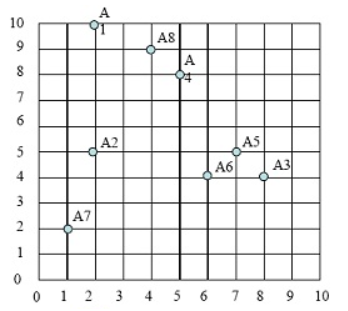
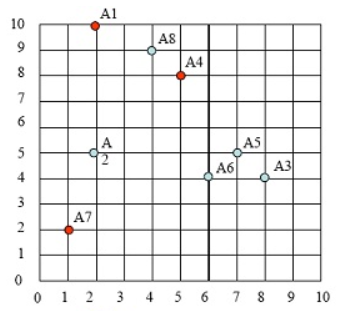
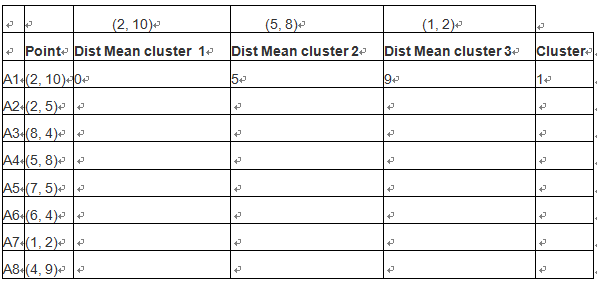

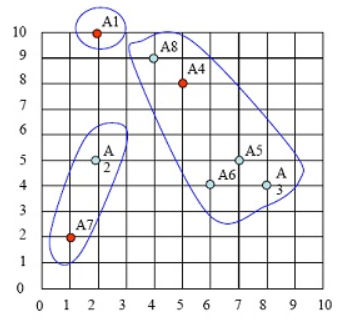
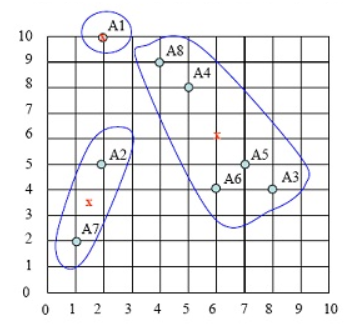
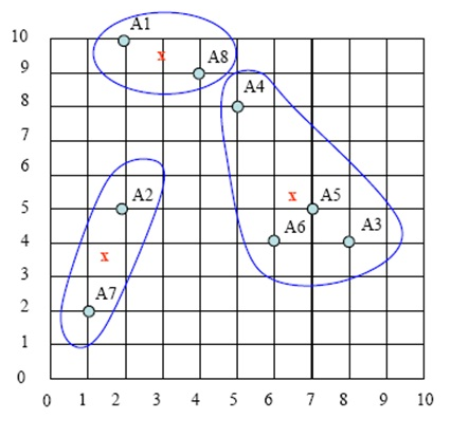 持续迭代,直到前后两次迭代不发生变化为止,如下:
持续迭代,直到前后两次迭代不发生变化为止,如下:
 " />
" />