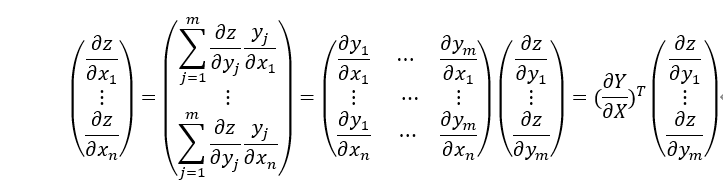第5章 梯度下降法
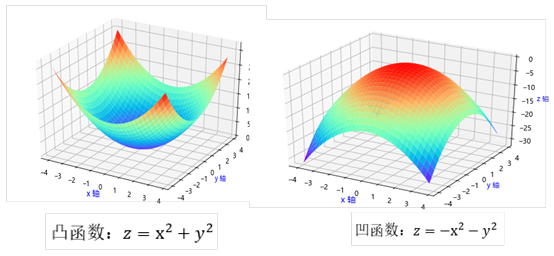
机器学习中一项重要任务就是求目标函数(或称为损失函数)的极小值或极大值。通过求目标函数的极值来确定相关权重参数,从而确定模型。如何求目标函数(注,这里的目标函数如果没有特别说明,一般指凸函数)的极值?最常用的一种方法就是梯度下降法。接下来我们将介绍梯度下降法及几种变种方法。
5.1.梯度下降法
梯度不仅是走向极值的方向,而且是下降最快的方向。
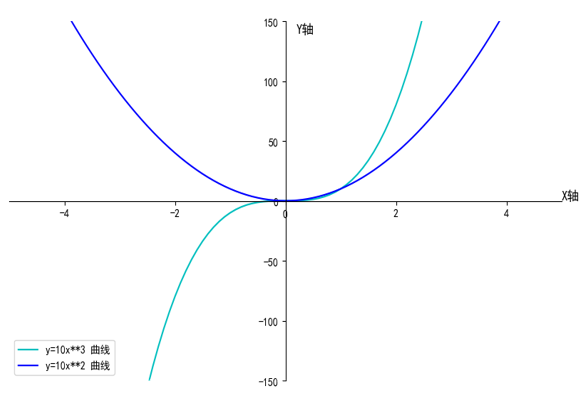
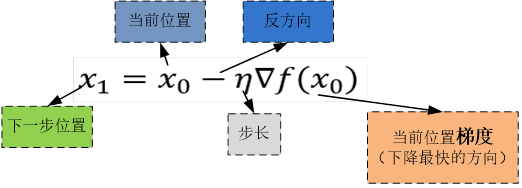
假设函数f(x)的有最小值,如图5-4所示。梯度下降法的数学表达式为:

其中
1、参数λ称为步长或学习率,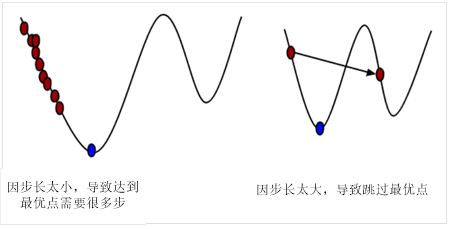
图5-1 学习率对寻找最优点过程的影响
2、这里为何取梯度的负值?
从图5-2可知,无论从左到右还是从右到左,沿梯度的负方向都是指向极小值(如果梯度正方向将指向函数的极大值)。
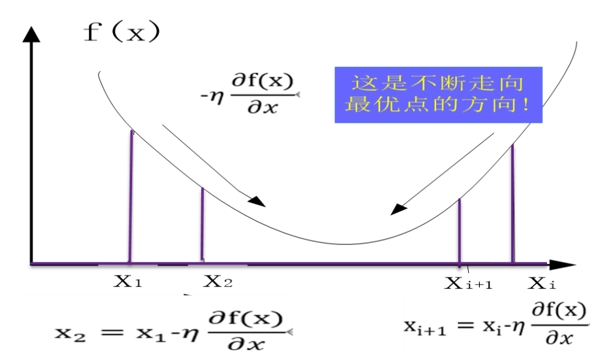
图5-2 梯度下降法示意图
如何理解沿梯度是函数值下降最快的方向呢?下面进行简单说明。
根据导数的定义及泰勒公式,可得函数梯度与函数增量、自变量增量之间的关系。

如果 足够小,则可以忽略高阶无穷小项,从而得到:
足够小,则可以忽略高阶无穷小项,从而得到:

由于 。
。
其中 为
为 与
与 之间的夹角,由于
之间的夹角,由于 ,因此,
,因此,
如果 ,此时,当
,此时,当 与
与 一定时,沿梯度的反方向下降最快。
一定时,沿梯度的反方向下降最快。
【说明】为何取负梯度?
求极小值,梯度的方向实际就是函数在此点下降最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号。
如果求极大值,则取梯度的正方向即可。
5.2 单变量函数的梯度下降法
假设函数 ,
,
使用梯度下降法,得到极值点。具体采用迭代法,沿梯度方向(或梯度负方向)逐步靠近极值点,如下图所示:
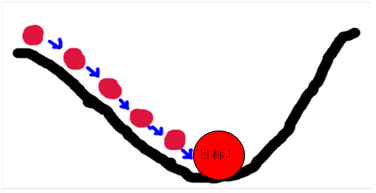
具体实现方法:
用迭代法求函数 的最优点。
的最优点。
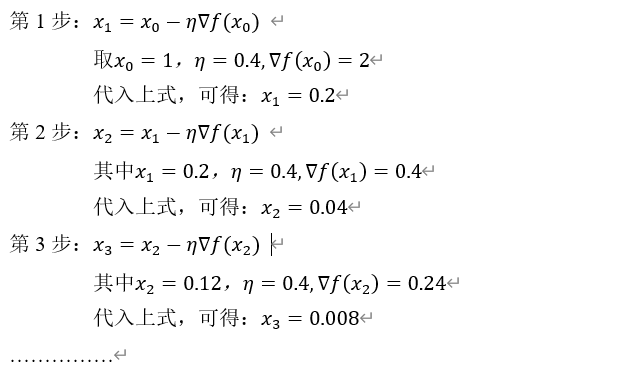
用python代码实现:
|
1 2 3 4 5 6 7 8 9 |
import numpy as np #求函数f(x)=x**2+3的最优点 #定义初始值及学习步长 x1=2.0 delta=0.4 for i in range(1,8): x1 = x1- delta*2*x1 print("x{}:{:.4f}".format(i,x1)) |
运行结果:
x1:0.4000
x2:0.0800
x3:0.0160
x4:0.0032
x5:0.0006
x6:0.0001
x7:0.0000
练习:用梯度下降法求函数 的极值点(迭代3次或以上),并用python实现这个过程。
的极值点(迭代3次或以上),并用python实现这个过程。
5.3 多变量函数的梯度下降法
如何用梯度下降方法求极值?以下通过一个简单示例来说明。
假设 ,该函数的最小值点为(0,0),用梯度下降法来一步步逼近这个最小值点。
,该函数的最小值点为(0,0),用梯度下降法来一步步逼近这个最小值点。
假设从点(1,3)开始,学习率设为 ,函数f(X)的梯度为:
,函数f(X)的梯度为:

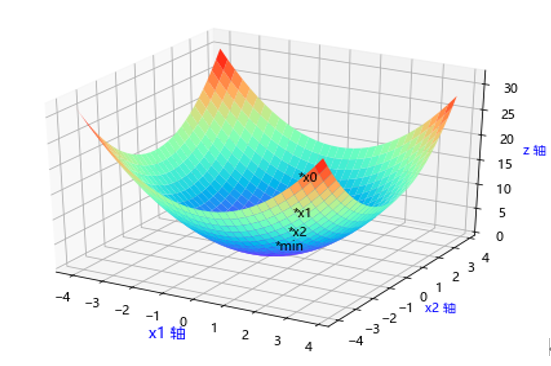
梯度方向是下降最快的方向,如下图所示:
实现上图的python代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 画制x1^2 + x2^2 from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D %matplotlib inline plt.rcParams['font.sans-serif']=['Microsoft YaHei'] fig = plt.figure() ax = Axes3D(fig) X = np.arange(-4, 4, 0.25) Y = np.arange(-4, 4, 0.25) X, Y = np.meshgrid(X, Y) Z = X**2 + Y**2 # 具体函数方法可用 help(function) 查看,如:help(ax.plot_surface) ax.plot_surface(X, Y, Z, cmap='rainbow') ax.set_xlabel('x1 轴',color='b',fontsize='12') ax.set_ylabel('x2 轴',color='b') ax.set_zlabel('z 轴',color='b') # 在图形上标注梯度下降的一些点 ax.text3D(3,-4,25,'*x0') ax.text3D(2.4,-3.2,16,'*x1') ax.text3D(1.9,-2.56,10.2,'*x2') ax.text3D(0,0,0,'*min') plt.show() |

用Python实现代码以上过程:
|
1 2 3 4 5 6 7 8 9 |
import numpy as np #定义初始值及学习步长 x1,x2=1.0,3.0 delta=0.1 for i in range(1,60): x1,x2 = np.array([x1,x2])- delta*np.array([2*x1,2*x2]) if i%10==0: print("x1:{:.4f},x2:{:.4f}".format(x1,x2)) |
运行结果
x1:0.1074,x2:0.3221
x1:0.0115,x2:0.0346
x1:0.0012,x2:0.0037
x1:0.0001,x2:0.0004
x1:0.0000,x2:0.0000
练习:
用梯度下降法求函数 的最优点,并用python实现并可视化。
的最优点,并用python实现并可视化。
5.4 梯度下降法的应用
梯度可以通过迭代的方法来求极值点,但更重要的作用是通过这个过程,来求梯度中的权重参数,从而确定模型。
例如,
求梯度时,往往涉及很多样本,根据这些样本更新参数。每次更新时,如何选择样本是有讲究的。
如果样本总数不大,我们每次更新梯度时,可以使用所有样本。但如果样本比较大,如果每次都用所有样本更新,在性能上不是一个好的方法,这时我们可以采用其它方案,这样既保证效果,又不影响性能。训练时根据样本选择方案不同,大致可分为:
(1)随机梯度下降法
每次求梯度时,不是使用所有样本的数据,而是每次随机选取一个样本来求梯度。这种方法每次更新梯度较快,但这种方法更新梯度振幅较大,如果样本较大,这样方法也非常耗时,效果也不很理想。
(2)批量梯度下降法
针对随机梯度下降法的不足,人们又想到一个两全其美的方法,即批量随机梯度下降法,这种方法每次更新梯度时,随机选择一个批量来更新梯度。这种方法有更好稳定性,同时性能方面也不错,尤其适合与样本比较大时,优势更加明显。
用梯度下降法拟合一条直线:

其中: 为参数。
为参数。
假设y为真实值,根据不同的样本x,代入 便可得到预测值。
便可得到预测值。
我们的目标是尽量使真实值y与预测值 尽可能接近,换句话,就是使它们之间的距离,通过不断学习样本,不断更新参数
尽可能接近,换句话,就是使它们之间的距离,通过不断学习样本,不断更新参数![\theta=[\theta_0,{\theta}_1]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f3511b2010234d5846dbe1b750af373f.gif) ,使以下目标函数的值最小。
,使以下目标函数的值最小。

即:
使用批量梯度下降法处理以上这个回归问题,具体算法如下:

写成矩阵的形式:

用X表示m个样本: ,这是一个
,这是一个 矩阵
矩阵
 这是一个
这是一个 矩阵
矩阵
 内积的形状为:
内积的形状为:
 这是一贯mx1向量,
这是一贯mx1向量,
使用矩阵向量方式定义损失值:

5.5 用Python实现批量梯度下降法
批量梯度下降法用Python实现:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import numpy as np import matplotlib.pyplot as plt #设置图形支持中文属性 plt.rcParams['font.family'] = 'SimHei' #设置字体 plt.rcParams['font.size'] = 10 #设置字体大小 plt.rcParams['axes.unicode_minus']=False #坐标轴的负号正常显示 #便于notebook在线交互 %matplotlib inline def costFunctionJ(x,y,theta): '''代价函数''' m = np.size(x, axis = 0) predictions =np.dot(x,theta) err=predictions - y j=np.dot(err.T,err)/(2*m) return j def gradientDescent(x,y,theta,alpha,num_iters): ''' alpha为学习率 num_iters为迭代次数 ''' m = len(y) n = len(theta) temp = np.array(np.zeros([n,num_iters])) # 用来暂存每次迭代更新的theta值,是一个矩阵形式 j_history = np.array(np.zeros([num_iters,1])) # #记录每次迭代计算的代价值 for i in range(num_iters): # 遍历迭代次数 h = np.dot(x,theta) temp[:,i] = (theta - (alpha/m)*np.dot(x.T,(h-y))).reshape(2,) theta = temp[:,i].reshape(2,1) j_history[i] = costFunctionJ(x,y,theta) return theta,j_history,temp x = np.array([1,3,1,4,1,6,1,5,1,1,1,4,1,3,1,4,1,3.5,1,4.5,1,2,1,5]).reshape(12,2) theta = np.array([0,2]).reshape(2,1) y = np.array([1,2,3,2.5,1,2,2.2,3,1.5,3,1,3]).reshape(12,1) |
训练模型并可视化运行结果
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 求代价函数值 j = costFunctionJ(x,y,theta) plt.figure(figsize=(15,5)) plt.subplot(1,2,1) plt.scatter(x[:,1],y[:,0],c='r',label='真实数据') # 画梯度下降前的图像 plt.plot(x[:,1],np.dot(x,theta),label = '测试数据') plt.legend(loc = 'best') plt.title('训练之前') theta, j_history, temp = gradientDescent(x,y,theta,0.01,100) print('最终j_history值:\n',j_history[-1]) print('最终theta值:\n',theta) #print('每次迭代的代价值:\n',j_history) #print('theta值更新历史:\n',temp) plt.subplot(1,2,2) plt.scatter(x[:,1],y[:,0],c='r',label = '真实数据') # 画梯度下降后的图像 plt.plot(x[:,1],np.dot(x,theta),label = '预测数据') plt.legend(loc = 'best') plt.title('训练之后') plt.show() |
运行结果如下:
最终j_history值:
[0.10784944]
最终theta值:
[[-0.27223179]
[ 0.6187312 ]]
可视化结果如下:
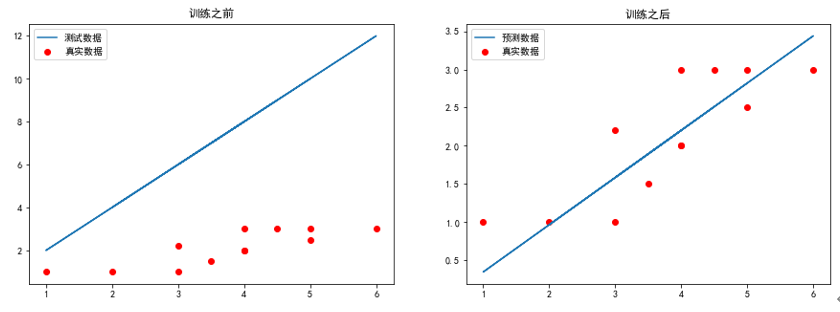
【说明】
5.6np.array与np.mat的区别
1.生成数组所需数据格式不同
np.mat可以从string或list中生成;而np.array只能从list中生成。
2.生成的数组计算方式不同
np.array生成数组,用np.dot()表示内积,(*)号或np.multiply()表示对应元素相乘。
np.mat生成数组,(*)和np.dot()相同,都表示内积,对应元素相乘只能用np.multiply()。
3.生成维度不同
np.mat只生成2维,np.array可生成n维。
建议使用array格式,因很多numpy函数返回值都是array格式。
5.7 用Python实现随机梯度下降法
1.定义损失函数、梯度函数
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import numpy as np import matplotlib.pyplot as plt #设置图形支持中文属性 plt.rcParams['font.family'] = 'SimHei' #设置字体 plt.rcParams['font.size'] = 10 #设置字体大小 plt.rcParams['axes.unicode_minus']=False #坐标轴的负号正常显示 #便于notebook在线交互 %matplotlib inline def costFunctionJ(x_i,y_i,theta): '''代价函数''' #m = np.size(x_i, axis = 0) predictions =np.dot(x_i,theta) err=predictions - y_i j=np.dot(err.T,err)/(2) return j def gradientDescent(x,y,theta,alpha,num_iters): ''' alpha为学习率 num_iters为迭代次数 ''' m = len(y) n = len(theta) temp = np.array(np.zeros([n,num_iters])) # 用来暂存每次迭代更新的theta值,是一个矩阵形式 j_history = np.array(np.zeros([num_iters,1])) # #记录每次迭代计算的代价值 for i in range(num_iters): # 遍历迭代次数 #每次随机取一个样本 rand_i = np.random.randint(len(x)) h = np.dot(x[rand_i],theta) temp[:,i] = theta - alpha*np.dot(x[rand_i].T.reshape(n,1),(h-y[rand_i])) theta = temp[:,i] j_history[i] = costFunctionJ(x[rand_i],y[rand_i],theta) return theta,j_history,temp #通过以下方式生成x的值 #生成x1的值 x1=np.array([3,4,6,5,1,4,3,4,3.5,4.5,2,5]) #与全是1的向量按行拼接 x=np.hstack([np.ones((len(x1),1)), x1.reshape(-1,1)]) theta = np.array([0,2]) m = len(y) y = np.array([1,2,3,2.5,1,2,2.2,3,1.5,3,1,3]).reshape(m,1) |
2.运行梯度函数及可视化运行结果
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 求代价函数值 j = costFunctionJ(x,y,theta) plt.figure(figsize=(15,5)) plt.subplot(1,2,1) plt.scatter(x[:,1],y[:,0],c='r',label='真实数据') # 画梯度下降前的图像 plt.plot(x[:,1],np.dot(x,theta),label = '测试数据') plt.legend(loc = 'best') plt.title('训练之前') theta, j_history, temp = gradientDescent(x,y,theta,0.01,100) print('最终j_history值:\n',j_history[-1]) print('最终theta值:\n',theta) #print('每次迭代的代价值:\n',j_history) #print('theta值更新历史:\n',temp) plt.subplot(1,2,2) plt.scatter(x[:,1],y[:,0],c='r',label = '真实数据') # 画梯度下降后的图像 plt.plot(x[:,1],np.dot(x,theta),label = '预测数据') plt.legend(loc = 'best') plt.title('训练之后') plt.show() |
3.运行结果
最终j_history值:
[0.07909981]
最终theta值:
[-0.25281579 0.60842649]
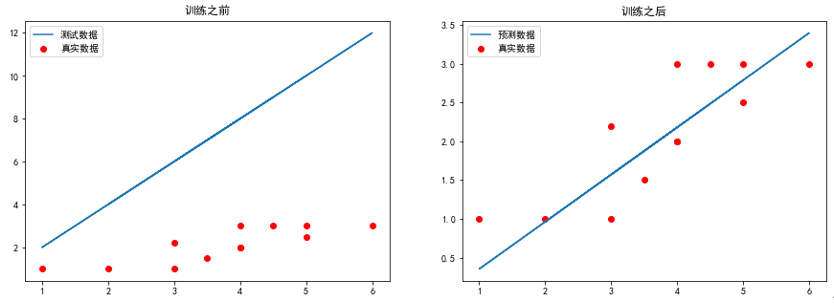
【练习】
把数据集改为:
m = 100000
x1 = np.random.normal(size = m)
X = x1.reshape(-1,1)
y = 4. * x1 + 3. +np.random.normal(0,3,size = m)
x= np.hstack([np.ones((len(x1),1)), X])





![\nabla f(x)=[\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\cdots,\frac{\partial f}{\partial x_n}]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f3c73e2ee602059c209f5ea00ecb2a0c.gif)