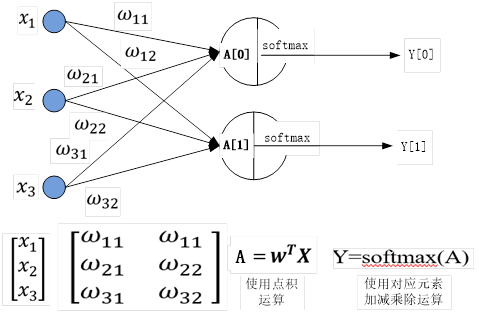
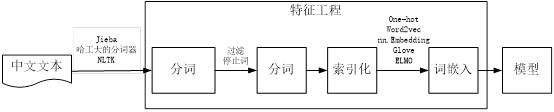
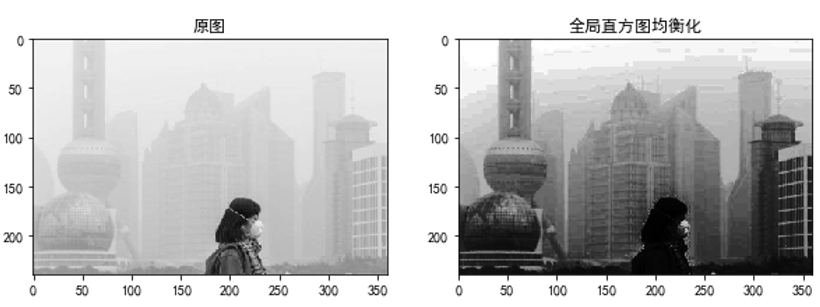
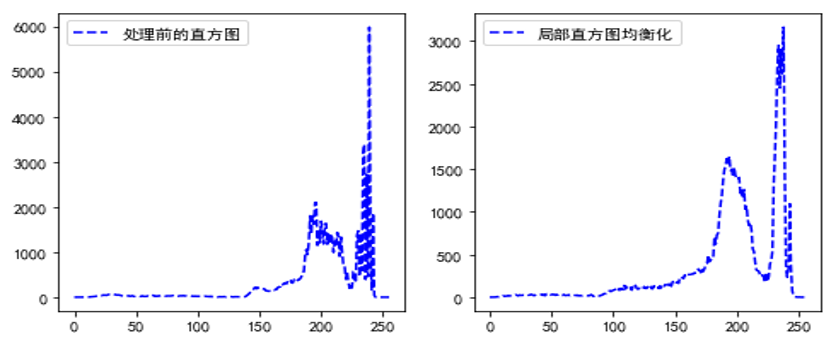
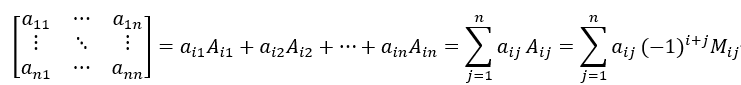第2 章 预处理结构化数据
2.1 预处理缺失值
2.1.1 数据生成
|
|
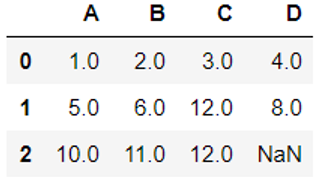
import pandas as pd from io import StringIO csv_data = '''A,B,C,D 1.0,2.0,3.0,4.0 5.0,6.0,,8.0 10.0,11.0,12.0,''' #StringIO以字符串的形式读取数据,并转换为dataframe的格式 df = pd.read_csv(StringIO(csv_data)) df |
运行结果为:
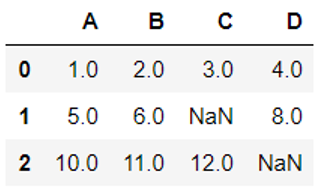
2.1.2查看缺失数据
查看各列缺失数据个数
A 0
B 0
C 1
D 1
dtype: int64
由此可知,C,D两列各有一个缺失或NaN数据。
2.1.3删除含缺失数据的特征或样本
|
|
#删除含缺失值的样本(或记录)或特征,这是删除df副本 df.dropna() #删除含缺失值的列 df.dropna(axis=1) #只删除所有列都是缺失值的行 df.dropna(how='all') # 保留至少4个为非缺失值的记录 df.dropna(thresh=4) #删除指定列行含缺失值的行 df.dropna(subset=['C']) |
2.1.4填充缺失值
|
|
#把缺失值填充为0 df.fillna(0) #把缺失值填充为对应列的平均值 from sklearn.preprocessing import Imputer imr = Imputer(missing_values='NaN', strategy='mean', axis=0) imr = imr.fit(df) imputed_data = imr.transform(df.values) imputed_data |
【说明】
strategy还可以是:median,most_frequent
这里Imputer是sklearn中的转换器类,主要用于数据转换。这些类中常用方法是fit和transform。fit用于参数识别并构建相应数据的补齐模型,而transform方法则是根据fit构建的模型进行缺失数据的补齐。
Imputer方法创建一个预处理对象,其中strategy为默认缺失值的字符串,默认为NaN;示例中选择缺失值替换方法是均值(默认),还可以选择使用中位数和众数进行替换,即strategy值设置为median或most_frequent;后面的参数axis用来设置输入的轴,默认值为0,即使用列做计算逻辑。然后使用预处理对象的fit_transform方法对df(数据框对象)进行处理,该方法是将fit和transform组合起来使用。
2.1.5用前后数据填充缺失值
|
|
# 用后面的值替换缺失值 df.fillna(method='backfill') |
运行结果

|
|
#用前面的值替换缺失值 df.fillna(method='pad') |
运行结果
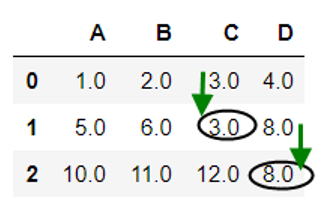
|
|
# 用后面的值替代缺失值,限制每列只能替代一个缺失值 df.fillna(method='bfill', limit=1) |
(6)不同列的缺失值,用不同值填充
|
|
# 用不同值替换不同列的缺失值 df.fillna({'C': 4, 'D': 3.2}) |
运行结果

2.2 处理类别数据
类别数据分为标称特征和有序特征,有序特征指类别的值是有序的或可以排序的,如体恤衫的尺寸:XL>L>M.而标称特征是不具备排序的特性,如体恤衫的颜色,对颜色进行大小比较是不合常理的。一般类标(分类标签)采用标称特征。
2.2.1生成数据
|
|
import pandas as pd df = pd.DataFrame([ ['green', 'M', 10.1, 'a'], ['red', 'L', 13.5, 'b'], ['blue', 'XL', 15.3, 'a']]) df.columns = ['color', 'size', 'price', 'classlabel'] df |
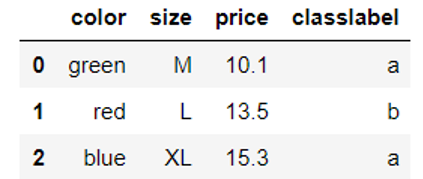
2.2.2有序特征的映射
这里size特征为有序特征,对该特征可以采用有序数字化处理。
|
|
#构建一个对应关系 size_mapping = { 'XL': 3, 'L': 2, 'M': 1} df['size'] = df['size'].map(size_mapping) df |
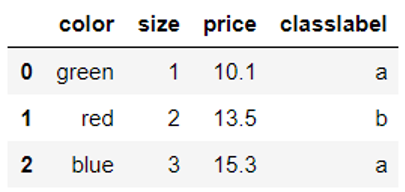
如果我们想还原,可以采用逆对应或逆字典inv_size_mapping = {v: k for k, v in size_mapping.items()}
|
|
inv_size_mapping = {v: k for k, v in size_mapping.items()} #inv_size_mapping df['size'].map(inv_size_mapping) df |
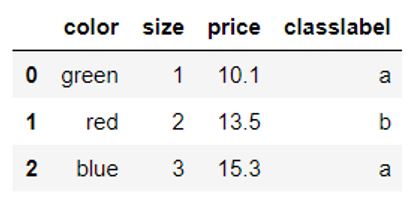
2.2.3标签的转换
|
|
#找出类标签列所有不同类别,然后索引化 import numpy as np class_mapping = {label:idx for idx,label in enumerate(np.unique(df['classlabel']))} class_mapping |
{'a': 0, 'b': 1}
|
|
#在对应列进行转换 df['classlabel'] = df['classlabel'].map(class_mapping) df |
运行结果
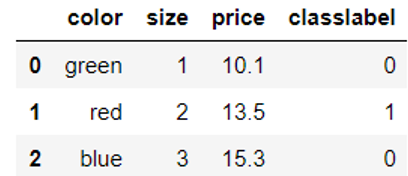
此外,也可以用sklearn中的LabelEncoder类将字符串类标转换为整数。
2.2.4 sklearn中常用的预处理函数
sklearn中常用的预处理函数及其功能大致有:
sklearn特征处理常用函数:
| 类名 |
功能 |
说明 |
| StandardScaler |
数据预处理(归一化) |
标准化,基于特征矩阵的列,将特征值转换至服从标准正态分布 |
| MinMaxScaler |
数据预处理(归一化) |
区间缩放,基于最大最小值,将特征值转换到[0, 1]区间上 |
| Normalizer |
数据预处理(归一化) |
基于特征矩阵的行,将样本向量转换为“单位向量” |
| Binarizer |
数据预处理(二值化) |
基于给定阈值,将定量特征按阈值划分 |
| OneHotEncoder |
数据预处理(哑编码) |
将定性数据编码为定量数据 |
| Imputer |
数据预处理(缺失值计算) |
计算缺失值,缺失值可填充为均值等 |
| PolynomialFeatures |
数据预处理(多项式数据转换) |
多项式数据转换 |
| FunctionTransformer |
数据预处理(自定义单元数据转换) |
使用单变元的函数来转换数据 |
| VarianceThreshold |
特征选择(Filter) |
方差选择法 |
| SelectKBest |
特征选择(Filter) |
可选关联系数、卡方校验、最大信息系数作为得分计算的方法 |
| RFE |
特征选择(Wrapper) |
递归地训练基模型,将权值系数较小的特征从特征集合中消除 |
| SelectFromModel |
特征选择(Embedded) |
训练基模型,选择权值系数较高的特征 |
| PCA |
降维(无监督) |
主成分分析法 |
| LDA |
降维(有监督) |
线性判别分析法 |
|
|
from sklearn.preprocessing import LabelEncoder class_le = LabelEncoder() y = class_le.fit_transform(df['classlabel'].values) y |
运行结果为
array([0, 1, 0], dtype=int64)
2.2.5标称特征转换为独热编码(One-Hot)
可以利用有序特征一般转换为整数,具体可采用sklearn中的LabelEncoder类将字符串类标转换为整数,示例代码如下:
|
|
from sklearn.preprocessing import LabelEncoder #获取对应特征的值 X = df[['color', 'size', 'price']].values color_le = LabelEncoder() #对X的第一列进行转换 X[:, 0] = color_le.fit_transform(X[:, 0]) X |
运行结果
array([[1, 1, 10.1],
[2, 2, 13.5],
[0, 3, 15.3]], dtype=object)
如果把标称特征转换为整数,算法将假定gree大于blue,red大于gree,虽然算法这一假设不很合理,而且能够生成有用的结果,然而,这个结果可能不是最优的。
如何生成更好或更合理的结果?这里就要引入独热编码(one-hot encoding)技术,这种技术的理念就是创建一个新的虚拟特征,该虚拟特征的列数就是类别个数,其值为二进制,每行只有一个1,其他都是0,值为1的对应该类别。
如将color特征,共有3种类别,所以将该转换为三个新的特征:blue、gree和red,
如果是blue,新特征就是[1,0,0],如果是gree,新特征就是[0,1,0].
独热编码可用sklearn.preprocessing中的OneHotEncoder类来实现,具体代码如下:
|
|
from sklearn.preprocessing import OneHotEncoder #初始化OneHotEncoder需指明转换特征所在的位置,或指明采用非稀疏矩阵格式 ohe = OneHotEncoder(categorical_features=[0],sparse=False) ohe.fit_transform(X) |
运行结果:
array([[ 0. , 1. , 0. , 1. , 10.1],
[ 0. , 0. , 1. , 2. , 13.5],
[ 1. , 0. , 0. , 3. , 15.3]])
这种方法先把字符转换为整数,然后把整数转换为虚拟特征,是否有更简单的方法?一步就实现呢?采用pandas的get_dummies方法就可以,它将把字符串直接转换为独热编码。以下为具体代码:
|
|
pd.get_dummies(df[['price', 'color', 'size']]) |
运行结果
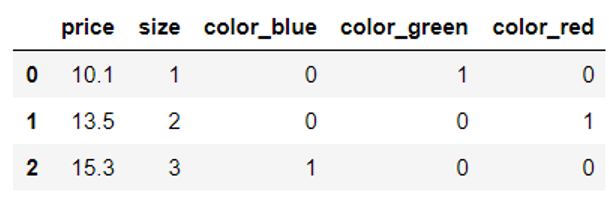
2.3合并数据
在MySQL的多表查询章节中,我们介绍了两表关联问题,具体请看如下图形;
(图2-1 多表关联)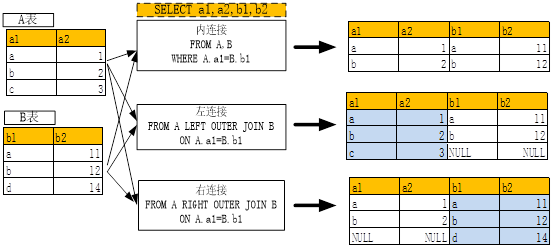
如果现在把表换成数据文件或数据集,该如何实现呢?Python中有类似方法,把连接的关键字有JION改为MERGE一下就可,其它稍作修改,具体请看下表:
(表2-1 两个DataFrame数据集关联格式表)
| 关联方式 |
关联语句 |
| df1内连接df2 |
pd.merge(df1,df2,on='key') |
| pd.merge(df1,df2,on='key',how='inner') |
| pd.merge(df1,df2,left_on='key',right_on='key',how='inner') |
| df1左连接df2 |
pd.merge(df1,df2,on='key',how='left') |
| df1右连接df2 |
pd.merge(df1,df2,on='key',how='right') |
| df1全连接df2 |
pd.merge(df1,df2,on='key',how='outer') |
下面同时示例来说明以上命令的具体使用。
|
|
from pandas import DataFrame import pymysql df1=DataFrame({'key':['a','a','b','c','c'],'data1':range(5)},columns=['key','data1']) df2=DataFrame({'key':['a','b','d'],'data2':range(3)},columns=['key','data2']) df1 |
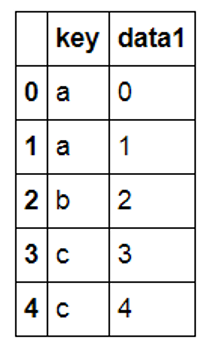
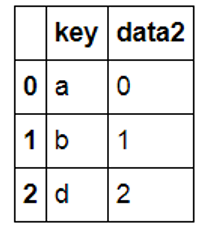
|
|
###内连接的几种方式 df3=pd.merge(df1,df2,on='key') df4=pd.merge(df1,df2,on='key',how='inner') df5=pd.merge(df1,df2,left_on='key',right_on='key',how='inner') ###df1与df2左连接 df_l=pd.merge(df1,df2,on='key',how='left') df_l |

|
|
###df1与df2右连接 df_r=pd.merge(df1,df2,on='key',how='right') ###df1与df2进行全连接 df_a=pd.merge(df1,df2,on='key',how='outer') |
两个集合连接以后,有些值可能为空或为NaN,NaN值有时计算不方便,我们可以把NaN修改为其它值,如为0值等,如果要修改或补充为0值,该如何操作呢?非常方便,利用DataFrame的fillna函数即可。其使用方法如下:
|
|
df_a.fillna(0) ##把NaN修改为0 |
2.4 离散化连续数据
上节我们介绍了有时便于数据分析,需要把两个或多个数据集合并在一起,这在大数据的分析或竞赛中是经常干的事。不过有时为便于分析,需要把一些连续性数据离散化或进行拆分,这也是数据分析常用方法,如对年龄字段,可能需转换成年龄段,这样可能更好地对数据的进行分类或预测,这种处理方式往往能提升分类或预测性能,这种方法又称为离散化或新增衍生指标等。
如何离散化连续性数据?在一般开发语言中,可以通过控制语句来实现,但如果分类较多时,这种方法不但繁琐,效率也比较低。在Pandas中是否有更好方法?如果有,又该如何实现呢?
pandas有现成方法,如cut或qcut等,不需要编写代码,至于如何使用还是通过实例来说明。
|
|
import numpy as np import pandas as pd from pandas import DataFrame df9=DataFrame({'age':[21,25,30,32,36,40,45,50],'type':['1','2','1','2','1','1','2','2']},columns=['age','type']) level=[20,30,40,50] ##划分为(20,30],(30,40],(40,50] groups=['A','B','C'] ##对应标签为A,B,C df9['age_t']=pd.cut(df9['age'],level,labels=groups) ##新增字段为age_t df10=df9[['age','age_t','type']] df10 |
对连续性字段进行离散化是机器学习常用方法,此外,对一些类型字段,如上例中type字段,含有1,2两种类型,实际上1,2两种类型是平等,它们只是代表不同类型,并无大小区别,如果在回归分析中如果用1、2代入算法中,则与业务含义就不相符了,对这种情况,我们该如何处理呢?
在机器学习中通常把这些分类变量或字段转换为“指标矩阵”或“哑变量矩阵”,具体做法就是,假设该字段或变量有k种取值(上例中type只有2中取值),则可派生出一个k列矩阵,矩阵值为0或1,0表示无对应分类,1表示有对应分类。我们可以编写程序实现,也可用Pandas中get_dummies函数来实现,具体实现请看以下示例。
|
|
dummies=pd.get_dummies(df10['type'],prefix='type') ##新增列名加前缀 dummies |
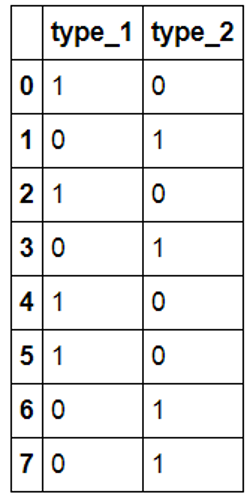
|
|
df10.join(dummies) ###通过位置索引与df10进行关联 |

【说明】
这种方法,在SparkML中有专门的算法--独热编码(OneHotEncoder),独热编码将标签指标映射为二值向量,其中最多一个单值。这种编码被用于将种类特征使用到需要连续特征的算法,如逻辑回归等。
2.5规范化数据
特征缩放是机器学习中常用方法,除少数算法(如决策树、随机森林)无需缩放外,大多算法可以通过缩放使其性能更佳。
缩放的方法大致有两种,归一化(normalization)和标准化(standardization)。归一化把特征值缩放到一个较小区间,如[0,1]或[-1,1]等,最大-最小缩放就是一个例子。

通过标准化我们可以使特征均值为0,方差为1或某个参数,使其符合正态分布。标准化方法保持了奇异值的有用信息,且降低算法受这些值的影响。

其中 ,
, 分别是样本某特征列的均值和标准差。以下是用sklearn.preprocessing的类来实现。
分别是样本某特征列的均值和标准差。以下是用sklearn.preprocessing的类来实现。
2.5.1导入数据
|
|
import pandas as pd import numpy as np df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data', header=None) #定义列名 df_wine.columns = ['酒等级', '酒精', '苹果酸', '灰', '灰分的碱度', '镁', '总酚', '黄酮类', '非类黄烷酚', '原花青素', '颜色强度', '色调', '稀释葡萄酒', '脯氨酸'] #查看前5行数据 df_wine.head() |
运行结果
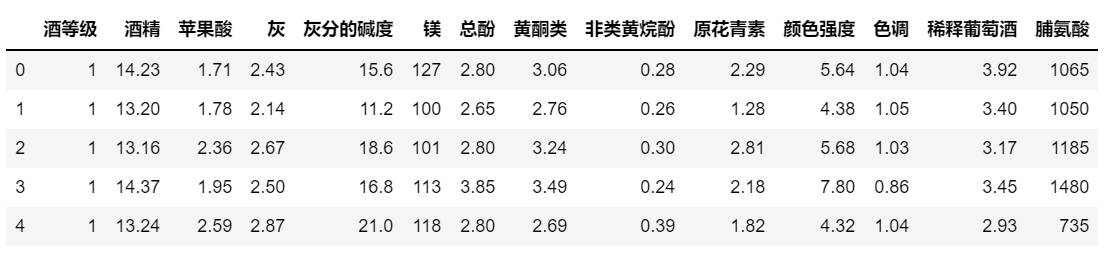
2.5.2探索数据
|
|
## 查看数据集总体情况 df_wine.info() |
运行结果
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 178 entries, 0 to 177
Data columns (total 14 columns):
酒等级 178 non-null int64
酒精 178 non-null float64
苹果酸 178 non-null float64
灰 178 non-null float64
灰分的碱度 178 non-null float64
镁 178 non-null int64
总酚 178 non-null float64
黄酮类 178 non-null float64
非类黄烷酚 178 non-null float64
原花青素 178 non-null float64
颜色强度 178 non-null float64
色调 178 non-null float64
稀释葡萄酒 178 non-null float64
脯氨酸 178 non-null int64
dtypes: float64(11), int64(3)
memory usage: 19.6 KB
由此可知:共有14列,178个样本
2.5.3查看各特征的统计信息
|
|
## 查看数据集各特征的统计信息 df_wine.describe() |
运行结果
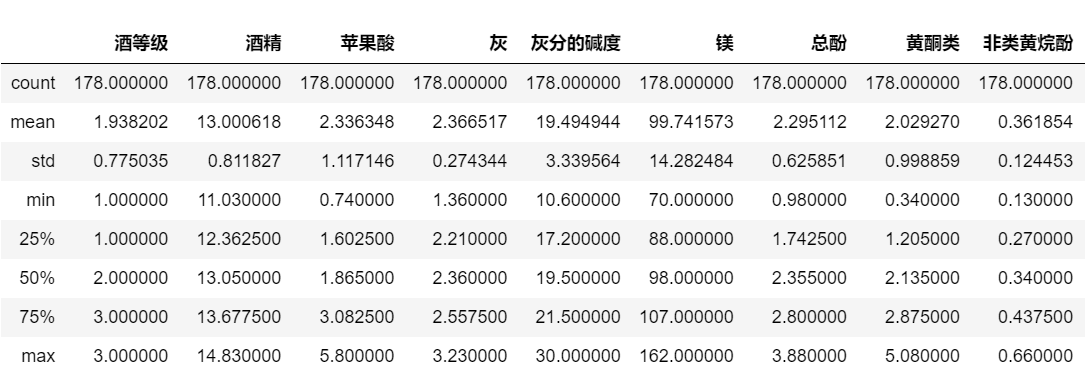
2.5.4查看是否有缺失数据
|
|
#查看数据质量,是否有空值、缺失值等 df_wine.isnull().sum() |
2.5.5划分数据
|
|
from sklearn.model_selection import train_test_split #把13个特征赋给X,标签赋给y X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) |
2.5.6对数据进行归一化
|
|
#对训练集、测试集进行归一化 from sklearn.preprocessing import MinMaxScaler mms = MinMaxScaler() X_train_norm = mms.fit_transform(X_train) X_test_norm = mms.transform(X_test) 对训练集、测试集进行标准化处理 |
|
|
from sklearn.preprocessing import StandardScaler stdsc = StandardScaler() X_train_std = stdsc.fit_transform(X_train) X_test_std = stdsc.transform(X_test) 为对这个过程进行可视化,我们以一个特征为例 |
|
|
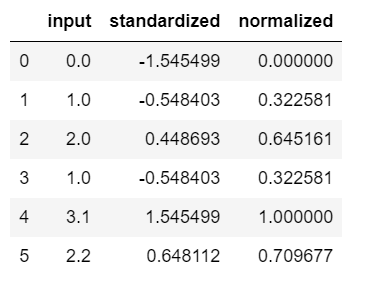
ex = pd.DataFrame([0, 1, 2 ,1, 3.1, 2.2]) # 标准化处理 ex[1] = (ex[0] - ex[0].mean()) / ex[0].std(ddof=0) # Please note that pandas uses ddof=1 (sample standard deviation) # by default, whereas NumPy's std method and the StandardScaler # uses ddof=0 (population standard deviation) # 归一化处理 ex[2] = (ex[0] - ex[0].min()) / (ex[0].max() - ex[0].min()) #重新命令dataframe的列名 ex.columns = ['input', 'standardized', 'normalized'] ex |
运行结果
2.6 选择有意义的特征
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说,从两个方面考虑来选择特征:
特征是否发散:
如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用。
特征与目标的相关性:
这点比较显见,与目标相关性高的特征,应当优选选择。
降维
降维方法比较多,如正则化降维、PCA、LDA等降维。
2.6.1 利用方差过滤法选择特征
|
|
from sklearn.feature_selection import VarianceThreshold #方差选择法,返回值为特征选择后的数据 #参数threshold为方差的阈值 VarianceThreshold(threshold=0.8).fit_transform(df_wine) |
这种方法比较粗糙,有时可能性能反而会下降。
2.6.2利用相关系数法
这里利用卡方来计算相关系数。用feature_selection库的SelectKBest类和chi2类来计算相关系数,选择特征的代码如下:
|
|
from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 #选择K个最好的特征,返回选择特征后的数据 X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values SelectKBest(chi2, k=4).fit_transform(X, y) |
2.6.3利用正则化方法选择特征
使用正则化惩罚项的模型,除了可用于筛选特征外,也可降维。这里使用feature_selection库的SelectFromModel类结合带L2惩罚项的逻辑回归模型来选择特征,具体代码如下:
|
|
from sklearn.feature_selection import SelectFromModel from sklearn.linear_model import LogisticRegression #带L2惩罚项的逻辑回归作为基模型的特征选择 X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values SelectFromModel(LogisticRegression(penalty="l2", C=0.1)).fit_transform(X, y) |
2.6.4基于树模型来选择特征
树模型中GBDT也可用于特征选择,使用feature_selection库的SelectFromModel类结合GBDT模型,来选择特征的代码如下:
|
|
from sklearn.feature_selection import SelectFromModel from sklearn.ensemble import GradientBoostingClassifier #GBDT作为基模型的特征选择 SelectFromModel(GradientBoostingClassifier()).fit_transform(X, y) |
2.6.5利用随机森林来选择特征
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import train_test_split import matplotlib import matplotlib.pyplot as plt %matplotlib inline plt.rcParams['font.sans-serif']=['SimHei'] # 以下适用用mac系统 # plt.rcParams['font.sans-serif'] = ['Arial Unicode MS'] plt.rcParams['axes.unicode_minus'] = False X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0) feat_labels = df_wine.columns[1:] #森林中树的数量,随机种子,并发数依据核数等 forest = RandomForestClassifier(n_estimators=10000,random_state=0,n_jobs=-1) forest.fit(X_train, y_train) importances = forest.feature_importances_ indices = np.argsort(importances)[::-1] for f in range(X_train.shape[1]): print("%2d) %-*s %f" % (f + 1, 30, feat_labels[indices[f]], importances[indices[f]])) plt.title('特征的重要性') plt.bar(range(X_train.shape[1]), importances[indices], color='lightblue', align='center') plt.xticks(range(X_train.shape[1]), feat_labels[indices], rotation=45) plt.xlim([-1, X_train.shape[1]]) plt.tight_layout() plt.show() |

2.7 特征组合
前面我们介绍了填充缺失值、对特征进行归一化、类别数据数值化或向量化、对连续型特征分段(或分箱)、找出更有意义的特征等预处理方法,这些方法在机器学习中经常使用。这些主要是对单个特征的处理,有时我们需要组合几个特征得到一个新特征,得到的这个新特征比原来的特征更有意义。假如我们预测房价的数据中包括经度和纬度,如果我们能组合这两个特征,得到一个有关街区的新特征,这个特征应该更具代表性。当然,组合前,我们可以把经度和纬度进行分组或分箱,然后在进行组合。
2.8 衍生新特征
这里以日期特征为例,由日期特征衍生出年、月、日、季度、星期几等新特征。这些特征有时更能刻画数据的规律,如是否周末、季度、工作日等的数据更有规律可循。具体代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import pandas as pd import numpy as np time_stamps = ['2022-03-08', '2022-07-13 15:45:05','2022-01-22','2022-06-27', '2022-12-25'] df = pd.DataFrame(time_stamps, columns=['Time']) ts_objs = np.array([pd.Timestamp(item) for item in np.array(df.Time)]) df['TS_obj'] = ts_objs df['年'] = df['TS_obj'].apply(lambda d: d.year) df['月'] = df['TS_obj'].apply(lambda d: d.month) df['日'] = df['TS_obj'].apply(lambda d: d.day) df['星期几'] = df['TS_obj'].apply(lambda d: d.dayofweek) df['是否周末']=["Y" if (i==0 or i==6) else "N" for i in df['星期几']] #判断是否周末 df['本年第几天'] = df['TS_obj'].apply(lambda d: d.dayofyear) df['本年第几周'] = df['TS_obj'].apply(lambda d: d.weekofyear) df['季度'] = df['TS_obj'].apply(lambda d: d.quarter) df[['Time', '年', '月', '日', '季度', '星期几','是否周末', '本年第几天', '本年第几周']] |
运行结果如下:

 对称矩阵对角线上的值正好是个特征的方差,其它值为协方差。
对称矩阵对角线上的值正好是个特征的方差,其它值为协方差。 实现对角化,对角化上的特征值代表
实现对角化,对角化上的特征值代表 的信息量,对这些特征值进行排序后,就可获取较大一些特征值,而我们要找的这个变换就是由对称矩阵
的信息量,对这些特征值进行排序后,就可获取较大一些特征值,而我们要找的这个变换就是由对称矩阵 的特征向量构成的式(6.2)中矩阵Q。
的特征向量构成的式(6.2)中矩阵Q。![X=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_193e348a7f28c1809cf3be796d9e2409.gif) ,需要降到k维。
,需要降到k维。 ,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。
,注:这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。 的特征值与特征向量。
的特征值与特征向量。 使用PCA方法进行降维。
使用PCA方法进行降维。
 乘以原数据得到:
乘以原数据得到: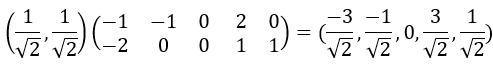
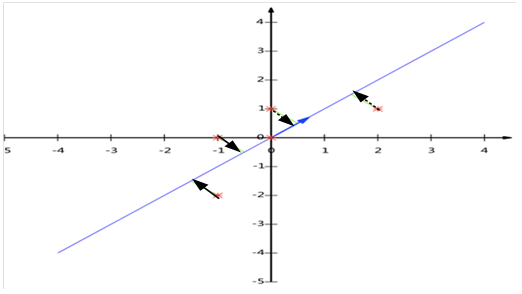
 就是原来的5个坐标在单位向量
就是原来的5个坐标在单位向量 上的投影。
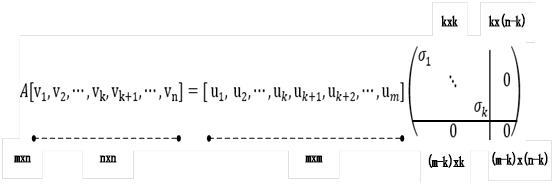
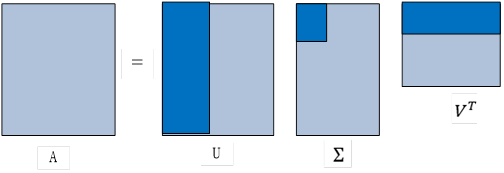
上的投影。 还是比较耗资源,这种情况下是否有更好的方法呢?针对这种情况,我们知道SVD中U(即左奇异矩阵)就是由
还是比较耗资源,这种情况下是否有更好的方法呢?针对这种情况,我们知道SVD中U(即左奇异矩阵)就是由 的特征向量构成的,为此,我们可以使用SVD的方法求协方差矩阵的特征值和特征向量,其它步骤与用特征值方法类似,具体步骤如下:
的特征向量构成的,为此,我们可以使用SVD的方法求协方差矩阵的特征值和特征向量,其它步骤与用特征值方法类似,具体步骤如下:![X=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_193e348a7f28c1809cf3be796d9e2409.gif) ,需要降到k维。
,需要降到k维。 与X进行内积,得到结果为:
与X进行内积,得到结果为:
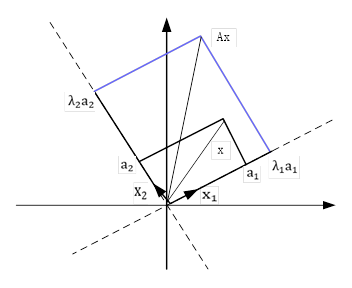
 的映射关系如下图所示。与例1相比,只是新轴的方向相反而已。
的映射关系如下图所示。与例1相比,只是新轴的方向相反而已。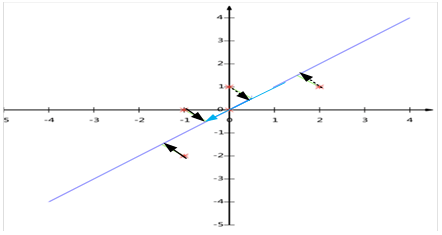



![Q=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_93938b91da7f312a1d0f1d659df6d89a.gif)
![[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_5b24c69c53879fbd5f252ac017989773.gif)
![x=[x_1,x_2,\cdots,x_n][a_1,a_2,\cdots,a_n ]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_54da61aa5df5c2c65fb17bb909f55636.gif)
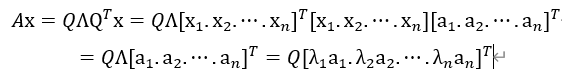
![[v_1,v_2,\cdots,v_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7b34aa5991785b3ab206ef9057dc99b9.gif)
![[Av_1,Av_2,\cdots,Av_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_3d5b0cb07ab9017032eed69d58a5addb.gif)









![[u_1,u_2,\cdots,u_k]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8b50705cfc07cea81ceb9a5d7b6e41b5.gif)
![[v_1,v_2,\cdots,v_k]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_03a5b82985c7a666ebaf3df2f688baea.gif)





![[v^1,v^2,\cdots,v^n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_33046d9a881830901d8dbd465bc032f1.gif)
![[\lambda_1,\lambda_2,\cdots,\lambda_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_bfaa2482f208825de2d1fa0ba296ae8d.gif)
![V=[v^1,v^2,\cdots,v^n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_2700ee472dbfa152766c8bacee1f685c.gif)




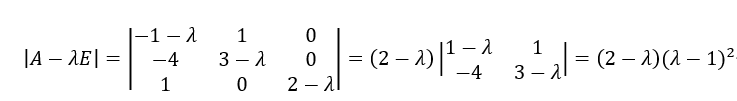

















![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\lambda \left(\begin{matrix}1&0 \\ 0&1 \end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b046ef3b8842d01335033942f3be0e6a.gif)
![\left[\left(\begin{matrix}1&2 \\ 0 &{-1} \end{matrix}\right)-\left(\begin{matrix}\lambda &0 \\ 0&\lambda\end{matrix}\right)\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_13aaa58fe526c17fb8e388c3f2701a67.gif)
![\left[\begin{matrix}{1-\lambda}&2 \\ 0 &{-1-\lambda} \end{matrix}\right]=0](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_a6409c423536da595e2dfd4575c97ba7.gif)




![a=[a_1,a_2,\cdots,a_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7580eb047fc7e8965f7cf6ade12c1f28.gif)
![b=[b_1,b_2,\cdots,b_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_97b19c4c617a7c377e1b76947d977621.gif)



![e=[e_1,e_2,\cdots,e_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_939995464ea64eaf49dfc487d512ea3e.gif)

![a=[a_1,a_2,\cdots,a_n ]=a\cdot e](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_ff16788a3c01e200e1fd1746f678d9e5.gif)











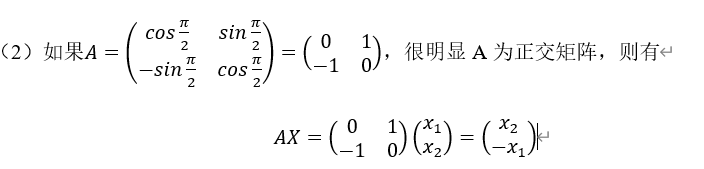













![X=\left[\begin{matrix} 1&0\\0&2\\0&0\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_d2f59da831f63960df062b81d88c92dd.gif)
![diag(v)=diag([v_1,v_2,\cdots,v_n]^T) \tag{2.14}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_7b808bdff924076375dc309e9167972c.gif)
![v=[v_1,v_2,\cdots,v_n]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f97782776ea99bbeabed0b72a74c97ed.gif)
![v=[v_1,v_2,\cdots,v_n]^T,x=[x_1,x_2,\cdots,x_n]^T](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_a80954bbcbbf9ed04dbcb7c68cdfef7a.gif)

![diag(v)^{-1}=diag([1/v_1,1/v_2,\cdots,1/v_n]^T)](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8499f5b16280c8e74d3147804496857b.gif)

















![A=\left[\begin{matrix}a_{1,1} & a_{1,2} &a_{1,3} \cr a_{2,1} & a_{2,2} &a_{2,3}\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_f4dc5ea10897d8df5c4f8e90ea57ad29.gif)
![A^T=\left[\begin{matrix}a_{1,1} & a_{2,1} \\ a_{1,2} & a_{2,2}\cr a_{1,3} & a_{2,3} \end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_3b249ae388e4585cfb6918b8a84c312a.gif)
![x^T=[x_1,x_2,\cdots,x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_b4758393f715cbecb421526c6f91676c.gif)



![\begin{aligned}A\odot B &=\left[\begin{matrix}1 & 2 & 3 \\ 4 & 5 &6\end{matrix}\right]\left[\begin{matrix}1 & 2 & 4 \\ 3 & 5 &0\end{matrix}\right]\\&=\left[\begin{matrix}1\times 1 & 2\times 2 & 3\times 4 \\ 4\times 3 &5\times 5 & 6\times 0\end{matrix}\right]\\&=\left[\begin{matrix}1 & 4 & 12 \\ 12 & 25 &0\end{matrix}\right]\end{aligned}](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_88204ec1dabec5f057b2b9283b6bbaf2.gif)