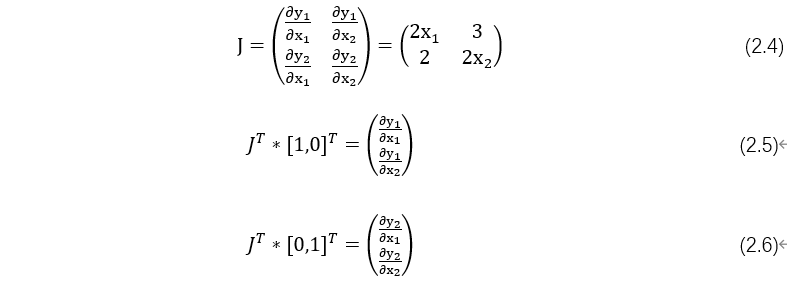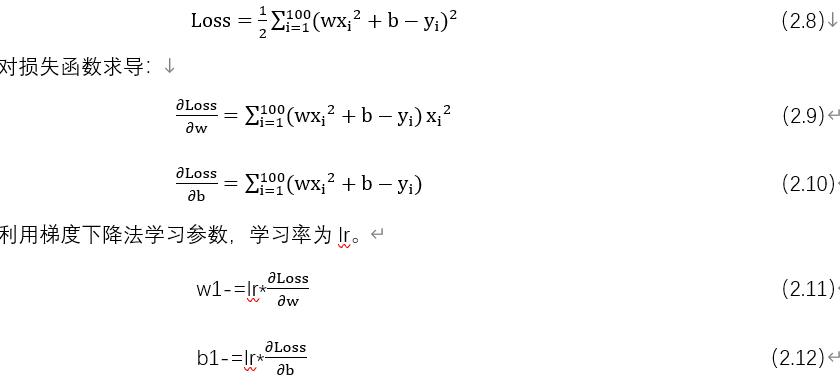第1章NumPy基础
请参考《机器学习的数学》中NumPy基础
第2章 PyTorch基础
PyTorch是Facebook团队于2017年1月发布的一个深度学习框架,虽然晚于TensorFlow、Keras等框架,但自发布之日起,其关注度就在不断上升,目前在GitHub上的热度已超过Theano、Caffe、MXNet等框架。
与PyTorch 1.0之前的版本相比,PyTorch 1.0版本增加了很多新功能,对原有内容进行了优化,并整合了caffe2,使用更方便,也大大增强其生产性,所以其热度在迅速上升。
PyTorch采用Python语言接口来实现编程,非常容易上手。它就像带GPU的NumPy,而且与Python一样都属于动态框架。PyTorch继承了Torch灵活、动态的编程环境和用户友好等特点,支持以快速和灵活的方式构建动态神经网络,还允许在训练过程中快速更改代码而不妨碍其性能,支持动态图形等尖端AI模型的能力,是快速实验的理想选择。本章主要介绍PyTorch的一些基础且常用的概念和模块,具体包括如下内容:
为何选择PyTorch
PyTorch环境的安装与配置
NumPy与Tensor
Tensor与Autograd
使用NumPy实现机器学习
使用Tensor及antograd实现机器学习
使用优化器自动微分等实现机器学习
使用TensorFlow2架构实现机器学习
2.1 为何选择PyTorch
PyTorch是一个建立在Torch库之上的Python包,旨在加速深度学习应用。它提供一种类似NumPy的抽象方法来表征张量(或多维数组),可以利用GPU来加速训练。由于 PyTorch 采用了动态计算图(Dynamic Computational Graph)结构,且基于tape的autograd 系统的深度神经网络。其他很多框架,比如 TensorFlow(TensorFlow2.0也加入了动态网络的支持)、Caffe、CNTK、Theano 等,采用静态计算图。通过PyTorch一种称之为反向模式自动微分(Reverse-mode auto-differentiation)的技术,你可以非常方便地构建网络。
torch是PyTorch中的一个重要包,它包含了多维张量的数据结构以及基于其上的多种数学操作。
自2015 年谷歌开源 TensorFlow以来,深度学习框架之争越来越激烈,全球多个看重 AI 研究与应用的科技巨头均在加大这方面的投入。从 2017 年年初发布以来,PyTorch 可谓是异军突起,在短时间内就取得了一系列成果,成为其中的明星框架。之后PyTorch进行了一些较大的版本更新,如0.4版本把Varable与Tensor进行了合并,增加了Windows的支持;1.0版本增加了JIT(全称Just-in-time compilation,即时编译,它弥补了研究与生产的部署的差距)、更快的分布式、C++扩展等。
目前PyTorch 1.0 稳定版已发布,它 从 Caffe2 和 ONNX 移植了模块化和产品导向的功能,并将它们和 PyTorch 已有的灵活、专注研究的特性相结合。PyTorch 1.0 中的技术已经让很多 Facebook 的产品和服务变得更强大,包括每天执行 60 亿次文本翻译。
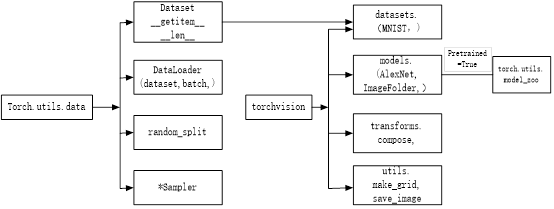
PyTorch由4个主要包组成,具体如下。
torch:类似于NumPy的通用数组库,可将张量类型转换为torch.cuda.TensorFloat,并在GPU上进行计算。
torch.autograd:用于构建计算图形并自动获取梯度的包。
torch.nn:具有共享层和损失函数的神经网络库。
torch.optim:具有通用优化算法(如SGD,Adam等)的优化包。
2.2 安装配置
在安装PyTorch时,请先核查当前环境是否有GPU,如果没有,则安装CPU版PyTorch;如果有,则安装GPU版PyTorch。
2.2.1 安装CPU版PyTorch
安装CPU版PyTorch的方法比较简单。PyTorch是基于Python开发的,所以如果没有安装Python则需要先安装Python,再安装PyTorch。具体步骤如下。
1. 下载Python
安装Python建议采用anaconda方式安装,先从Anaconda的官网:https://www.anaconda.com/distribution, 如图2-1 所示。
图2-1 下载Anaconda界面
下载Anaconda3的最新版本,如Anaconda3-2021.11-Linux-x86_64.sh,建议使用3系列,3系列代表未来发展。另外,下载时根据自己环境,选择操作系统等。
2. 安装Python
在命令行,执行如下命令,开始安装Python:
Anaconda3-2021.11-Linux-x86_64.sh
根据安装提示,直接按回车即可。其间会提示选择安装路径,如果没有特殊要求,可以按回车使用默认路径(~/ anaconda3),然后就开始安装。安装完成后,程序提示是否把anaconda3的binary路径加入到当前用户的.bashrc配置文件中,建议添加。添加以后,就可以使用python、ipython命令时自动使用Anaconda3的python环境。
3. 安装PyTorch
登录PyTorch官网(https://pytorch.org/),登录后,可看到如图2-2 所示界面,然后选择对应项。
图2-2 安装CPU版PyTorch
把第⑥项内容复制到命令行,执行即可。
conda install pytorch-cpu torchvision-cpu -c pytorch
(6)验证安装是否成功
启动Python,然后执行如下命令,如果没有报错,说明安装成功!
2.2.2 安装GPU版PyTorch
安装GPU版本的PyTorch稍微复杂一点,除需要安装Python、PyTorch,还需要安装GPU的驱动(如英伟达的Nvidia)及cuda、cuDNN计算框架,主要步骤如下。
1. 安装NVIDIA驱动
下载地址为https://www.nvidia.cn/Download/index.aspx?lang=cn。 登录可以看到如图2-3所示的界面。
图2-3 NVIDIA的下载界面
选择产品类型、操作系统等,然后点击搜索按钮,进入下载界面。
安装完成后,在命令行输入nvidia-smi,用来显示GPU卡的基本信息,如果出现如图2-4所示信息,则说明安装成功。如果报错,则说明安装失败,请搜索其他安装驱动的方法。
图2-4 显示GPU卡的基本信息
2. 安装CUDA
CUDA(Compute Unified Device Architecture,统一计算设备架构),是英伟达公司推出的一种基于新的并行编程模型和指令集架构的通用计算架构,它能利用英伟达GPU的并行计算引擎,比CPU更高效地解决许多复杂计算任务。安装CUDA 驱动时,需保证该驱动与NVIDIA GPU 驱动的版本一致,这样CUDA才能找到显卡。
3. 安装cuDNN
NVIDIA cuDNN是用于深度神经网络的GPU加速库。注册NVIDIA并下载cuDNN包,地址为https://developer.nvidia.com/rdp/cudnn-archive。
4. 安装Python及PyTorch
这步与2.2.1节安装CPU版PyTorch的步骤相同,只是选择CUDA时,不是选择None,而是选择对应CUDA的版本号,如图2-5所示。
图2-5 安装GPU版PyTorch
5. 验证
验证PyTorch安装是否成功的方法与2.2.1节一样,如果想进一步验证PyTorch是否在使用GPU,可以运行以下这段测试GPU的程序test_gpu.py。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
#cat test_gpu.py import torch if __name__ == '__main__': #测试 CUDA print("Support CUDA ?: ", torch.cuda.is_available()) x = torch.tensor([10.0]) x = x.cuda() print(x) y = torch.randn(2, 3) y = y.cuda() print(y) z = x + y print(z) # 测试 CUDNN from torch.backends import cudnn print("Support cudnn ?: ",cudnn.is_acceptable(x)) |
在命令行运行以下脚本:
python test_gpu.py
如果可以看到如图2-6所示的结果,说明安装GPU版PyTorch成功!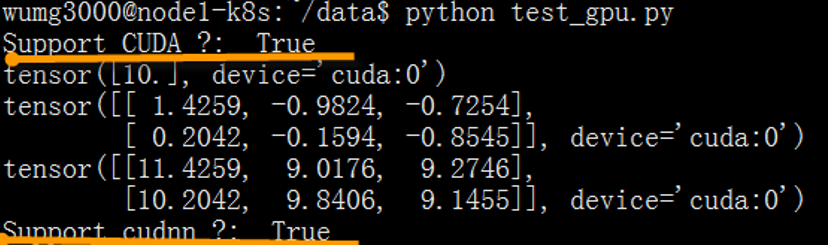
图2-6 运行test_gpu.py的结果
在命令行运行nvidia-smi,可以看到如图2-7所示界面。
图2-7 含GPU进程的显卡信息
2.3 Jupyter Notebook环境配置
Jupyter Notebook是目前Python比较流行的开发、调试环境,此前被称为 IPython Notebook。它以网页的形式打开,可以在网页页面中直接编写代码和运行代码,代码的运行结果(包括图形)也会直接显示,如在编程过程中添加注释、目录、图像或公式等内容。Jupyter Notebook具有以下特点。
编程时具有语法高亮、缩进、tab补全的功能。
可直接通过浏览器运行代码,同时在代码块下方展示运行结果。
以富媒体格式展示计算结果。富媒体格式包括:HTML,LaTeX,PNG,SVG等。
对代码编写说明文档或语句时,支持Markdown语法。
支持使用LaTeX编写数学性说明。
接下来介绍配置Jupyter Notebook的主要步骤。
1)生成配置文件。
|
|
jupyter notebook --generate-config |
将在当前用户目录下生成文件:.jupyter/jupyter_notebook_config.py
2)生成当前用户登录jupyter密码。打开ipython, 创建一个密文密码:
|
|
In [1]: from notebook.auth import passwd In [2]: passwd() Enter password: Verify password: |
3)修改配置文件。
|
|
vim ~/.jupyter/jupyter_notebook_config.py |
进行如下修改:
|
|
c.NotebookApp.ip='*' # 就是设置所有ip皆可访问 c.NotebookApp.password = u'sha:ce...刚才复制的那个密文' c.NotebookApp.open_browser = False # 禁止自动打开浏览器 c.NotebookApp.port =8888 #这是默认端口,也可指定其他端口 |
4)启动Jupyter Notebook。
|
|
#后台启动jupyter:不记日志: nohup jupyter notebook >/dev/null 2>&1 & |
在浏览器上,输入IP:port,即可看到如图2-8所示界面。
图2-8 Jupyter notebook主页界面
接下来就可以在浏览器进行开发调试PyTorch、Python等任务了。
2.4 NumPy与Tensor
第1章我们介绍了NumPy,知道其读取数据非常方便,而且还拥有大量的函数,所以深得数据处理、机器学习者喜爱。这节我们将介绍PyTorch的Tensor,它可以是零维(又称为标量或一个数)、一维、二维及多维的数组。其自称为神经网络界的NumPy, 它与NumPy相似,它们共享内存,它们之间的转换非常方便和高效。不过它们也有不同之处,最大的区别就是NumPy 会把 ndarray 放在 CPU 中加速运算,而由Torch 产生的 Tensor 会放在 GPU 中进行加速运算(假设当前环境有GPU)。
2.4.1 Tensor概述
对Tensor的操作很多,从接口的角度来划分,可以分为两类:
1)torch.function,如torch.sum、torch.add等,
2)tensor.function,如tensor.view、tensor.add等。
这些操作对大部分Tensor都是等价的,如torch.add(x,y)与x.add(y)等价。在实际使用时,可以根据个人爱好选择。
如果从修改方式的角度,可以分为以下两类。
1)不修改自身数据,如x.add(y),x的数据不变,返回一个新的tensor。
2)修改自身数据,如x.add_(y)(运行符带下划线后缀),运算结果存在x中,x被修改。
以下代码说明add与add_的区别。
|
|
import torch x=torch.tensor([1,2]) y=torch.tensor([3,4]) z=x.add(y) print(z) print(x) x.add_(y) print(x) |
运行结果如下:
tensor([4, 6])
tensor([1, 2])
tensor([4, 6])
2.4.2 创建Tensor
新建Tensor的方法很多,可以把列表或ndarray等数据对象直接转换为Tensor,也可以根据指定的形状构建。常见的构建Tensor的方法,可参考表2-1。
表2-1 常见的新建Tensor方法
| 函数 |
功能 |
| Tensor(*size) |
直接从参数构造一个的张量,支持list、numpy数组 |
| eye(row, column) |
创建指定行数,列数的二维单位tensor |
| linspace(start,end,steps) |
从step到end,均匀切分成steps份 |
| logspace(start,end,steps) |
从10^step, 到10^end,均匀切分成steps份 |
| rand/randn(*size) |
生成[0,1)均匀分布/标准正态分布数据 |
| ones(*size) |
返回指定shape的张量,元素初始为1 |
| zeros(*size) |
返回指定shape的张量,元素初始为0 |
| ones_like(t) |
返回与t的shape相同的张量,且元素初始为1 |
| zeros_like(t) |
返回与t的shape相同的张量,且元素初始为0 |
| arange(start,end,step) |
在区间[start,end)上以间隔step生成一个序列张量 |
| from_numpy(ndarray) |
从ndarray创建一个tensor |
下面举例说明。
|
|
import torch #根据list数据生成tensor torch.Tensor([1,2,3,4,5,6]) #根据指定形状生成tensor torch.Tensor(2,3) #根据给定的tensor的形状 t=torch.Tensor([[1,2,3],[4,5,6]]) #查看tensor的形状 t.size() #shape与size()等价方式 t.shape #根据已有形状创建tensor torch.Tensor(t.size()) |
【说明】注意torch.Tensor与torch.tensor的几点区别
1)torch.Tensor是torch.empty和torch.tensor之间的一种混合,但是,当传入数据时,torch.Tensor使用全局默认dtype(FloatTensor),torch.tensor从数据中推断数据类型。
2)torch.tensor(1)返回一个固定值1,而torch.Tensor(1)返回一个大小为1的张量,它是随机初始化的值。
举例如下。
|
|
import torch t1=torch.Tensor(1) t2=torch.tensor(1) print("t1的值{},t1的数据类型{}".format(t1,t1.type())) print("t2的值{},t2的数据类型{}".format(t2,t2.type())) |
运行结果如下:
t1的值tensor([3.5731e-20]),t1的数据类型torch.FloatTensor
t2的值1,t2的数据类型torch.LongTensor
下面来看一些根据一定规则,自动生成tensor的例子。
|
|
import torch #生成一个单位矩阵 torch.eye(2,2) #自动生成全是0的矩阵 torch.zeros(2,3) #根据规则生成数据 torch.linspace(1,10,4) #生成满足均匀分布随机数 torch.rand(2,3) #生成满足标准分布随机数 torch.randn(2,3) #返回所给数据形状相同,值全为0的张量 torch.zeros_like(torch.rand(2,3)) |
2.4.3 改变Tensor形状
在处理数据、构建网络层等过程中,我们经常需要了解Tensor的形状、改变Tensor的形状。与改变NumPy的形状类似,改变tenor的形状也有很多类似函数,具体可参考表2-2。 表2-2 为tensor常用修改形状的函数。
| 函数 |
说明 |
| size() |
返回张量的shape属性值,与函数shape(0.4版新增)等价 |
| numel(input) |
计算tensor的元素个数 |
| view(*shape) |
修改tensor的shape,与reshape(0.4版新增)类似,但view返回的对象与源tensor共享内存,修改一个另一个同时修改。Reshape将生成新的tensor,而且不要求源tensor是连续的。View(-1)展平数组。 |
| resize |
类似于view,但在size超出时会重新分配内存空间 |
| item |
若tensor为单元素,则返回pyton的标量 |
| unsqueeze |
在指定维度增加一个"1" |
| squeeze |
在指定维度压缩一个"1" |
下面来看一些实例。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import torch #生成一个形状为2x3的矩阵 x = torch.randn(2, 3) #查看矩阵的形状 x.size() #结果为torch.Size([2, 3]) #查看x的维度 x.dim() #结果为2 #把x变为3x2的矩阵 x.view(3,2) #把x展平为1维向量 y=x.view(-1) y.shape #添加一个维度 z=torch.unsqueeze(y,0) #查看z的形状 z.size() #结果为torch.Size([1, 6]) #计算Z的元素个数 z.numel() #结果为6 |
【说明】torch.view与torch.reshape的异同。
1)reshape()可以由torch.reshape(),也可由torch.Tensor.reshape()调用。view()只可由torch.Tensor.view()来调用。
2)对于一个将要被view的Tensor,新的size必须与原来的size与stride兼容。否则,在view之前必须调用contiguous()方法。
3)同样也是返回与input数据量相同,但形状不同的tensor。若满足view的条件,则不会copy,若不满足,则会copy。
4)如果你只想重塑张量,请使用torch.reshape。 如果您还关注内存使用情况并希望确保两个张量共享相同的数据,请使用torch.view。
2.4.4 索引操作
Tensor的索引操作与NumPy类似,一般情况下索引结果与源数据共享内存。从tensor获取元素除了可以通过索引,也可借助一些函数,常用的选择函数可参考表2-3。
表2-3 常用选择操作函数
| 函数 |
说明 |
| index_select(input,dim,index) |
在指定维度上选择一些行或列 |
| nonzero(input) |
获取非0元素的下标 |
| masked_select(input,mask) |
使用二元值进行选择 |
| gather(input,dim,index) |
在指定维度上选择数据,输出的形状与index(index的类型必须是LongTensor类型的)一致 |
| scatter_( input, dim, index, src) |
为gather的反操作,根据指定索引补充数据 |
以下为部分函数的实现代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import torch #设置一个随机种子 torch.manual_seed(100) #生成一个形状为2x3的矩阵 x = torch.randn(2, 3) #根据索引获取第1行,所有数据 x[0,:] #获取最后一列数据 x[:,-1] #生成是否大于0的Byter张量 mask=x>0 #获取大于0的值 torch.masked_select(x,mask) #获取非0下标,即行,列索引 torch.nonzero(mask) #获取指定索引对应的值,输出根据以下规则得到 #out[i][j] = input[index[i][j]][j] # if dim == 0 #out[i][j] = input[i][index[i][j]] # if dim == 1 index=torch.LongTensor([[0,1,1]]) torch.gather(x,0,index) index=torch.LongTensor([[0,1,1],[1,1,1]]) a=torch.gather(x,1,index) #把a的值返回到一个2x3的0矩阵中 z=torch.zeros(2,3) z.scatter_(1,index,a) |
2.4.5 广播机制
前文1.8节介绍了NumPy的广播机制,它是向量运算的重要技巧。PyTorch也支持广播规则,下面通过几个示例进行说明。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import torch import numpy as np A = np.arange(0, 40,10).reshape(4, 1) B = np.arange(0, 3) #把ndarray转换为Tensor A1=torch.from_numpy(A) #形状为4x1 B1=torch.from_numpy(B) #形状为3 #Tensor自动实现广播 C=A1+B1 #我们可以根据广播机制,手工进行配置 #根据规则1,B1需要向A1看齐,把B变为(1,3) B2=B1.unsqueeze(0) #B2的形状为1x3 #使用expand函数重复数组,分别的4x3的矩阵 A2=A1.expand(4,3) B3=B2.expand(4,3) #然后进行相加,C1与C结果一致 C1=A2+B3 |
2.4.6 逐元素操作
与NumPy一样,tensor也有逐元素操作,操作内容相似,但使用函数可能不尽相同。大部分数学运算都属于逐元操作,逐元素操作输入与输出的形状相同。,常见的逐元素操作,可参考表2-4。
表2-4常见逐元素操作
| 函数 |
说明 |
| abs/add |
绝对值/加法 |
| addcdiv(t,t1,t2,value=1) |
t1与t2的按元素除后,乘value加t |
| addcmul(t,t1,t2, value=1) |
t1与t2的按元素乘后,乘value加t |
| ceil/floor |
向上取整/向下取整 |
| clamp(t, min, max) |
将张量元素限制在指定区间 |
| exp/log/pow |
指数/对数/幂 |
| mul(或*)/neg |
逐元素乘法/取反 |
| sigmoid/tanh/softmax |
激活函数 |
| sign/sqrt |
取符号/开根号 |
【说明】这些操作均创建新的tensor,如果需要就地操作,可以使用这些方法的下划线版本,例如abs_。
以下为部分逐元素操作代码实例。
|
|
import torch t = torch.randn(1, 3) t1 = torch.randn(3, 1) t2 = torch.randn(1, 3) #t+0.1*(t1/t2) torch.addcdiv(t, t1, t2,value=0.1) #计算sigmoid torch.sigmoid(t) #将t限制在[0,1]之间 torch.clamp(t,0,1) #t+2进行就地运算 t.add_(2) |
2.4.7 归并操作
归并操作,顾名思义,就是对输入进行归并或合计等操作,这类操作的输入输出形状一般不相同,而且往往是输入大于输出形状。归并操作可以对整个tensor进行归并,也可以沿着某个维度进行归并。常见的归并操作可参考表2-5。
表2-5 常见的归并操作
| 函数 |
说明 |
| cumprod(t, axis) |
在指定维度对t进行累积 |
| cumsum |
在指定维度对t进行累加 |
| dist(a,b,p=2) |
返回a,b之间的p阶范数 |
| mean/median |
均值/中位数 |
| std/var |
标准差/方差 |
| norm(t,p=2) |
返回t的p阶范数 |
| prod(t)/sum(t) |
返回t所有元素的积/和 |
【说明】
归并操作一般涉及一个dim参数,指定沿哪个维进行归并。另一个参数是keepdim,说明输出结果中是否保留维度1,默认情况是False,即不保留。
以下为归并操作的部分代码。
|
|
import torch #生成一个含6个数的向量 a=torch.linspace(0,10,6) #使用view方法,把a变为2x3矩阵 a=a.view((2,3)) #沿y轴方向累加,即dim=0 b=a.sum(dim=0) #b的形状为[3] #沿y轴方向累加,即dim=0,并保留含1的维度 b=a.sum(dim=0,keepdim=True) #b的形状为[1,3] |
2.4.8 比较操作
比较操作一般进行逐元素比较,有些是按指定方向比较。常用的比较函数可参考表2-6。
表2-6 常用的比较函数
| 函数 |
说明 |
| eq |
比较tensor是否相等,支持broadcast |
| equal |
比较tensor是否有相同的shape与值 |
| ge/le/gt/lt |
大于/小于比较/大于等于/小于等于比较 |
| max/min(t,axis) |
返回最值,若指定axis,则额外返回下标 |
| topk(t,k,axis) |
在指定的axis维上取最高的K个值 |
以下是部分函数的代码实现。
|
|
import torch x=torch.linspace(0,10,6).view(2,3) #求所有元素的最大值 torch.max(x) #结果为10 #求y轴方向的最大值 torch.max(x,dim=0) #结果为[6,8,10] #求最大的2个元素 torch.topk(x,1,dim=0) #结果为[6,8,10],对应索引为tensor([[1, 1, 1] |
2.4.9 矩阵操作
机器学习和深度学习中存在大量的矩阵运算,用的比较多的有两种,一种是逐元素乘法,另外一种是点积乘法。PyTorch中常用的矩阵函数可参考表2-7。
表2-7 常用矩阵函数
| 函数 |
说明 |
| dot(t1, t2) |
计算张量(1D)的内积或点积 |
| mm(mat1, mat2)/bmm(batch1,batch2) |
计算矩阵乘法/含batch的3D矩阵乘法 |
| mv(t1, v1) |
计算矩阵与向量乘法 |
| t |
转置 |
| svd(t) |
计算t的SVD分解 |
【说明】
1)torch的dot与NumPy的dot有点不同,torch中dot对两个为1维张量进行点积运算,NumPy中的dot无此限制。
2)mm是对2维矩阵进行点积运算,bmm对含batch的3维矩阵进行点积运算。
3)转置运算会导致存储空间不连续,需要调用contiguous方法转为连续。
|
|
import torch a=torch.tensor([2, 3]) b=torch.tensor([3, 4]) torch.dot(a,b) #运行结果为18 x=torch.randint(10,(2,3)) y=torch.randint(6,(3,4)) torch.mm(x,y) x=torch.randint(10,(2,2,3)) y=torch.randint(6,(2,3,4)) torch.bmm(x,y) |
2.4.10 PyTorch与NumPy比较
PyTorch与NumPy有很多类似的地方,并且有很多相同的操作函数名称,或虽然函数名称不同但含义相同;当然也有一些虽然函数名称相同,但含义不尽相同。对此,有时很容易混淆,下面我们把一些主要的区别进行汇总,具体可参考表2-8。
表2-8 PyTorch与NumPy函数对照表
| 操作类别 |
NumPy |
PyTorch |
| 数据类型 |
np.ndarray |
torch.Tensor |
| np.float32 |
torch.float32; torch.float |
| np.float64 |
torch.float64; torch.double |
| np.int64 |
torch.int64; torch.long |
| 从已有数据构建 |
np.array([3.2, 4.3], dtype=np.float16) |
torch.tensor([3.2, 4.3],
dtype=torch.float16) |
| x.copy() |
x.clone() |
| np.concatenate |
torch.cat |
| 线性代数 |
np.dot |
torch.mm |
| 属性 |
x.ndim |
x.dim() |
| x.size |
x.nelement() |
| 形状操作 |
x.reshape |
x.reshape; x.view |
| x.flatten |
x.view(-1) |
| 类型转换 |
np.floor(x) |
torch.floor(x); x.floor() |
| 比较 |
np.less |
x.lt |
| np.less_equal/np.greater |
x.le/x.gt |
| np.greater_equal/np.equal/np.not_equal |
x.ge/x.eq/x.ne |
| 随机种子 |
np.random.seed |
torch.manual_seed |
2.5 Tensor与Autograd
在神经网络中,一个重要内容就是进行参数学习,而参数学习离不开求导,PyTorch是如何进行求导的呢?
现在大部分深度学习架构都有自动求导的功能,PyTorch也不列外,torch.autograd包就是用来自动求导的。autograd包为张量上所有的操作提供了自动求导功能,而torch.Tensor和torch.Function为autograd包的两个核心类,它们相互连接并生成一个有向非循环图。接下来我们先简单介绍tensor如何实现自动求导,然后介绍计算图,最后用代码实现这些功能。
2.5.1 自动求导要点
autograd包为对tensor进行自动求导,为实现对tensor自动求导,需考虑如下事项。
1)创建叶子节点(leaf node)的tensor,使用requires_grad参数指定是否记录对其的操作,以便之后利用backward()方法进行梯度求解。requires_grad参数默认值为False,如果要对其求导需设置为True,与之有依赖关系的节点自动变为True。
2)可利用requires_grad_()方法修改tensor的requires_grad属性。可以调用.detach()或with torch.no_grad():将不再计算张量的梯度,跟踪张量的历史记录。这点在评估模型、测试模型阶段常常使用。
3)通过运算创建的tensor(即非叶子节点),会自动被赋于grad_fn属性。该属性表示梯度函数。叶子节点的grad_fn为None。
4)最后得到的tensor执行backward()函数,此时自动计算各变在量的梯度,并将累加结果保存grad属性中。计算完成后,非叶子节点的梯度自动释放。
5)backward()函数接受参数,该参数应和调用backward()函数的Tensor的维度相同,或者是可broadcast的维度。如果求导的tensor为标量(即一个数字),backward中参数可省略。
6)反向传播的中间缓存会被清空,如果需要进行多次反向传播,需要指定backward中的参数retain_graph=True。多次反向传播时,梯度是累加的。
7)非叶子节点的梯度backward调用后即被清空。
8)可以通过用torch.no_grad()包裹代码块来阻止autograd去跟踪那些标记为.requesgrad=True的张量的历史记录。这步在测试阶段经常使用。
在整个过程中,PyTorch采用计算图的形式进行组织,该计算图为动态图,它的计算图在每次正向传播时,将重新构建。其他深度学习架构,如TensorFlow、Keras一般为静态图。接下来我们介绍计算图,用图的形式来描述就更直观了,该计算图为有向无环图(DAG)。
2.5.2计算图
计算图是一种有向无环图像,用图形方式表示算子与变量之间的关系,直观高效。如图2-9所示,圆形表示变量,矩形表示算子。如表达式z=wx+b可写成两个表示式:如果y=wx,则z=y+b。其中x、w、b为变量,是用户创建的变量,不依赖于其他变量,故又称为叶子节点。为计算各叶子节点的梯度,需要把对应的张量参数requires_grad属性设置为True,这样就可自动跟踪其历史记录。y、z是计算得到的变量,非叶子节点,z为根节点。mul和add是算子(或操作或函数)。这些变量及算子就构成一个完整的计算过程(或正向传播过程)。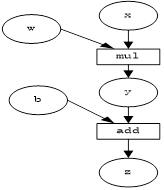
图2-9正向传播计算图
我们的目标是更新各叶子节点的梯度,根据复合函数导数的链式法则,不难算出各叶子节点的梯度。



PyTorch调用backward(),将自动计算各节点的梯度,这是一个反向传播过程,这个过程可用图2-9表示。在反向传播过程中,autograd沿着图2-10,从当前根节点z反向溯源,利用导数链式法则,计算所有叶子节点的梯度,并梯度值将累加到grad属性中。对非叶子节点的计算操作(或function)记录在grad_fn属性中,叶子节点的grad_fn值为None。
图2-10 梯度反向传播计算图
下面我们用代码实现这个计算图。
2.5.3 标量反向传播
PyTorch使用torch.autograd.backward来实现反向传播,backward函数的具体格式如下:
|
|
torch.autograd.backward( tensors, grad_tensors=None, retain_graph=None, create_graph=False, grad_variables=None) |
参数说明如下。
tensor: 用于计算梯度的tensor。
grad_tensors: 在计算非标量的梯度时会用到。其形状一般需要和前面的tensor保持一致。
retain_graph: 通常在调用一次backward后,pytorch会自动把计算图销毁,如果要想对某个变量重复调用backward,则需要将该参数设置为True
create_graph: 当设置为True的时候可以用来计算更高阶的梯度
grad_variables:这个参数后面版本中应该会丢弃,直接使用grad_tensors就好了。
假设x、w、b都是标量,z=wx+b,对标量z调用backward(),我们无须对backward()传入参数。以下是实现自动求导的主要步骤。
1)定义叶子节点及算子节点。
|
|
import torch #定义输入张量x x=torch.Tensor([2]) #初始化权重参数W,偏移量b、并设置require_grad属性为True,为自动求导 w=torch.randn(1,requires_grad=True) b=torch.randn(1,requires_grad=True) #实现正向传播 y=torch.mul(w,x) #等价于w*x z=torch.add(y,b) #等价于y+b #查看x,w,b页子节点的requite_grad属性 print("x,w,b的require_grad属性分别为:{},{},{}".format(x.requires_grad,w.requires_grad,b.requires_grad)) |
运行结果如下:
x,w,b的require_grad属性分别为:False,True,True
2)查看叶子节点、非叶子节点的其他属性。
|
|
#查看非叶子节点的requres_grad属性, print("y,z的requires_grad属性分别为:{},{}".format(y.requires_grad,z.requires_grad)) #因与w,b有依赖关系,故y,z的requires_grad属性也是:True,True #查看各节点是否为叶子节点 print("x,w,b,y,z的是否为叶子节点:{},{},{},{},{}".format(x.is_leaf,w.is_leaf,b.is_leaf,y.is_leaf,z.is_leaf)) #x,w,b,y,z的是否为叶子节点:True,True,True,False,False #查看叶子节点的grad_fn属性 print("x,w,b的grad_fn属性:{},{},{}".format(x.grad_fn,w.grad_fn,b.grad_fn)) #因x,w,b为用户创建的,为通过其他张量计算得到,故x,w,b的grad_fn属性:None,None,None #查看非叶子节点的grad_fn属性 print("y,z的是否为叶子节点:{},{}".format(y.grad_fn,z.grad_fn)) #y,z的是否为叶子节点:, |
3)自动求导,实现梯度方向传播,即梯度的反向传播。
|
|
#基于z张量进行梯度反向传播,执行backward之后计算图会自动清空, z.backward() #如果需要多次使用backward,需要修改参数retain_graph为True,此时梯度是累加的 #z.backward(retain_graph=True) #查看叶子节点的梯度,x是叶子节点但它无须求导,故其梯度为None print("参数w,b的梯度分别为:{},{},{}".format(w.grad,b.grad,x.grad)) #参数w,b的梯度分别为:tensor([2.]),tensor([1.]),None #非叶子节点的梯度,执行backward之后,会自动清空 print("非叶子节点y,z的梯度分别为:{},{}".format(y.grad,z.grad)) #非叶子节点y,z的梯度分别为:None,None |
2.5.4 非标量反向传播
2.5.3小节我们介绍了当目标张量为标量时,调用backward()无须传入参数。目标张量一般是标量,如我们经常使用的损失值Loss,一般都是一个标量。但也有非标量的情况,后面我们介绍的Deep Dream的目标值就是一个含多个元素的张量。如何对非标量进行反向传播呢?PyTorch有个简单的原则,不让张量对张量求导,只允许标量对张量求导,因此,如果目标张量对一个非标量调用backward(),需要传入一个gradient参数,该参数也是张量,而且其形状需要与调用backward()的张量形状相同。
为什么要传入一个张量gradient?这是为了把张量对张量求导转换为标量对张量求导。这有点拗口,我们举一个例子来说,假设目标值为 传入的参数为
传入的参数为 ,那么就可把对loss的求导,转换为对
,那么就可把对loss的求导,转换为对 标量的求导。即把原来
标量的求导。即把原来 得到雅可比矩阵(Jacobian)乘以张量
得到雅可比矩阵(Jacobian)乘以张量 ,便可得到我们需要的梯度矩阵。
,便可得到我们需要的梯度矩阵。
1、 非标量简单示例
我们先看目标张量为非标量的简单实例。
|
|
X= torch.ones(2,requires_grad=True) Y = X**2+3 Y.backward() |
运行后会报错:RuntimeError: grad can be implicitly created only for scalar outputs。这是因为张量y为非标量所致。
如何避免类似错误呢?我们手工计算Y的导数。已知:
![X=[x_1,x_2]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8de545821487bd0e59c2a63bba38810d.gif)
![Y=[x_1^2+3,x_2^2+3]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_c703a1571d623ee3a87630f1639a035f.gif)
如何求 呢?
呢?
Y为一个向量,如果我们想办法把这个向量转变成一个标量不就好了?比如我们可以对Y求和,然后用求和得到的标量在对X求导,这样不会对结果有影响,例如:


这个过程可写成如下代码。
|
|
x = torch.ones(2,requires_grad=True) y = x**2+3 y.sum().backward() print(x.grad) #tensor([2., 2.]) |
可以看到对y求和后再计算梯度没有报错,结果也与预期一样。
实际上,对Y求和就是等价于Y点积一个的全为1的向量或矩阵。即,而这个向量矩阵V也就是我们需要传入的grad_tensors参数。(点积只是相对于一维向量而言的,对于矩阵或更高为的张量,可以看做是对每一个维度做点积。)
2.非标量复杂实例
(1)定义叶子叶子节点及计算节点
|
|
import torch #定义叶子节点张量x,形状为1x2 x= torch.tensor([[2, 3]], dtype=torch.float, requires_grad=True) #初始化Jacobian矩阵 J= torch.zeros(2 ,2) #初始化目标张量,形状为1x2 y = torch.zeros(1, 2) #定义y与x之间的映射关系: #y1=x1**2+3*x2,y2=x2**2+2*x1 y[0, 0] = x[0, 0] ** 2 + 3 * x[0 ,1] y[0, 1] = x[0, 1] ** 2 + 2 * x[0, 0] |
(2)手工计算y对x的梯度
我们先手工计算一下y对x的梯度,为了验证PyTorch的backward的结果是否正确。
y对x的梯度是一个雅可比矩阵,各项的值,我们可通过以下方法进行计算。
假设 ,不难得到:
,不难得到: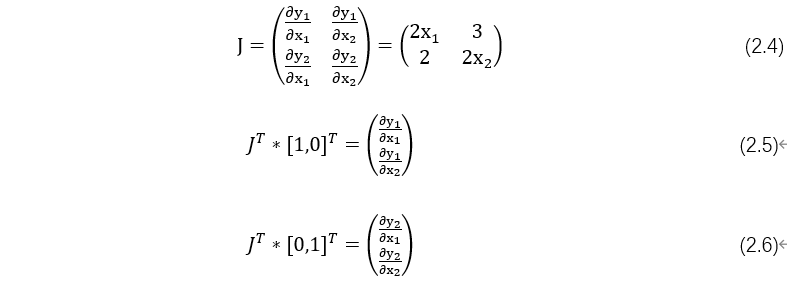
当 时,
时,
(3)调用backward获取y对x的梯度
这里我们可以分成两步的计算。首先让v=(1,0)得到y_1对x的梯度,然后使v=(0,1),得到y_2对x的梯度。这里因需要重复使用backward(),需要使参数retain_graph=True,具体代码如下:
|
|
#生成y1对x的梯度 y.backward(torch.Tensor([[1, 0]]),retain_graph=True) J[0]=x.grad #梯度是累加的,故需要对x的梯度清零 x.grad = torch.zeros_like(x.grad) #生成y2对x的梯度 y.backward(torch.Tensor([[0, 1]])) J[1]=x.grad #显示jacobian矩阵的值 print(J) |
运行结果如下:
tensor([[4., 3.],[2., 6.]])
这个结果与手工运行的式(2.5)结果一致。
(4)如果V值不对,将导致错误结果。
如果取v=[1,1]将导致错误结果,代码示例如下:
|
|
y.backward(torch.Tensor([[1, 1]])) print(x.grad) #结果为tensor([[6., 9.]]) |
这个结果与我们手工运算的不符,显然这个结果是错误的,错在哪里呢?这个结果的计算过程是:

由此,错在v的取值错误,通过这种方式得的到并不是y对x的梯度。
3.小结
1)PyTorch不允许张量对张量求导,只允许标量对张量求导,求导结果是和自变量同型的张量。
2)为避免直接对张量求导,可以利用torch.autograd.backward()函数中的参数grad_tensors, 把它转换标量来求导。 y.backward(v) 的含义是:先计算 loss = torch.sum(y * v),然后求 loss 对(能够影响到 y 的)所有变量 x 的导数。这里,y和 v是同型 Tensor。也就是说,可以理解成先按照 v对y的各个分量加权,加权求和之后得到真正的 loss,再计算这个 loss 对于所有相关变量的导数。
3)PyTorch中的计算图是动态计算图,动态计算图有两个特点:正向传播是立即执行的;反向传播后计算图立即销毁。我们把PyTorch使用自动微分的计算图的生命周期用图2-11来表示。
图2-11 PyTorch计算图的生命周期
2.5.5切断一些分支的反向传播
训练网络时,有时候我们希望保持一部分的网络参数不变,只对其中一部分的参数进行调整;或者只训练部分分支网络,并不让其梯度对主网络的梯度造成影响,这时候可以使用detach()函数来切断一些分支的反向传播。
detach_()将张量从创建它的计算图(Graph)中分离,把它作为叶子节点,其grad_fn=None且requires_grad=False。
假设y是作为x的函数,而z则是y和x的函数。如果我们想计算z关于x的梯度,但由于某种原因,我们希望将y视为一个常数。为此,我们可以分离y来返回一个新变量c,c变量与y具有相同的值, 但丢弃计算图中如何计算y的任何信息。 换句话说,梯度不会向后流经c到x。 因此,下面的反向传播函数计算z=c*x关于x的偏导数,同时将c作为常数处理,即有 ,而不是把
,而不是把 关于x的偏导数,
关于x的偏导数, 。
。
|
|
import torch x = torch.ones(2,requires_grad=True) y = x**2+3 ##对分离变量y,生成一个新变量c。 c = y.detach() z = c*x z.sum().backward() x.grad==c ## tensor([True, True]) x.grad ## tensor([4., 4.]) c.grad_fn==None ## True c.requires_grad ##False |
由于变量c记录了y的计算结果,在y上调用反向传播, 将得到y= x**2+3关于的x的导数,即2*x。
|
|
x.grad.zero_() y.sum().backward() x.grad == 2 * x ##tensor([True, True]) |
2.6 使用NumPy实现机器学习
前面我们介绍了NumPy、Tensor的基础内容,对如何用NumPy、Tensor操作数组有了一定认识。为了加深大家对PyTorch的谅解,本章剩余章节将分别用NumPy、Tensor、autograd、nn及optimal实现同一个机器学习任务,比较它们的异同及优缺点,从而加深对PyTorch的理解。
首先,我们用最原始的NumPy实现一个有关回归的机器学习任务,不用PyTorch中的包或类。这种方法的代码可能会多一点,但每一步都是透明的,有利于理解每步的工作原理。
主要步骤分析如下。
首先,是给出一个数组x,然后基于表达式: ,加上一些噪声数据到达另一组数据y。
,加上一些噪声数据到达另一组数据y。
然后,构建一个机器学习模型,学习表达式 的两个参数w,b。利用数组x,y的数据训练模型。
的两个参数w,b。利用数组x,y的数据训练模型。
最后,采用梯度下降法,通过多次迭代,学习到w、b的值。
1)导入需要的库。
|
|
# -*- coding: utf-8 -*- import numpy as np %matplotlib inline from matplotlib import pyplot as plt |
2)生成输入数据x及目标数据y。设置随机数种子,生成同一个份数据,以便用多种方法进行比较。
|
|
np.random.seed(100) x = np.linspace(-1, 1, 100).reshape(100,1) y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1) |
3)查看x,y数据分布情况。
|
|
# 画图 plt.scatter(x, y) plt.show() |
运行结果如图2-12所示。

图2-12 NumPy实现的源数据
4)初始化权重参数。
|
|
# 随机初始化参数 w1 = np.random.rand(1,1) b1 = np.random.rand(1,1) |
5)训练模型。
定义损失函数,假设批量大小为100: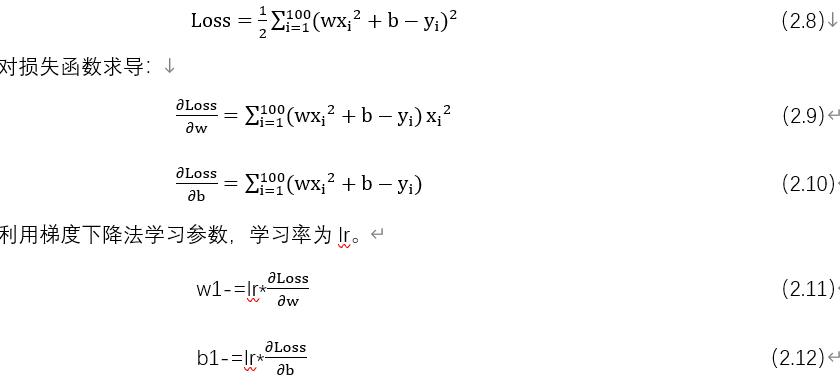
用代码实现上面这些表达式:
|
|
lr =0.001 # 学习率 for i in range(800): # 正向传播 y_pred = np.power(x,2)*w1 + b1 # 定义损失函数 loss = 0.5 * (y_pred - y) ** 2 loss = loss.sum() #计算梯度 grad_w=np.sum((y_pred - y)*np.power(x,2)) grad_b=np.sum((y_pred - y)) #使用梯度下降法,是loss最小 w1 -= lr * grad_w b1 -= lr * grad_b |
6)查看可视化结果。
|
|
plt.plot(x, y_pred,'r-',label='predict',linewidth=4) plt.scatter(x, y,color='blue',marker='o',label='true') # true data plt.xlim(-1,1) plt.ylim(2,6) plt.legend() plt.show() print(w1,b1) |
运行结果如图2-13所示。

图2-13 可视化NumPy学习结果
[[2.98927619]] [[2.09818307]]
从结果看来,学习效果还是比较理想的。
2.7 使用Tensor及Autograd实现机器学习
2.6节可以说是纯手工完成一个机器学习任务,数据用NumPy表示,梯度学习是自己定义并构建学习模型。这种方法适合于比较简单的情况, 如果稍微复杂一些, 代码量将几何级增加。 是否有更方便的方法呢? 这节我们将使用PyTorch的自动求导的一个
包——autograd,利用这个包及对应的Tensor, 便可利用自动反向传播来求梯度,无须手工计算梯度。以下是具体实现代码。
1)导入需要的库。
|
|
import torch %matplotlib inline from matplotlib import pyplot as plt |
2)生成训练数据,并可视化数据分布情况。
|
|
torch.manual_seed(100) dtype = torch.float #生成x坐标数据,x为tenor,形状为100x1 x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) #生成y坐标数据,y为tenor,形状为100x1,另加上一些噪声 y = 3*x.pow(2) +2+ 0.2*torch.rand(x.size()) # 画图,把tensor数据转换为numpy数据 plt.scatter(x.numpy(), y.numpy()) plt.show() |
运行结果如图2-14所示。
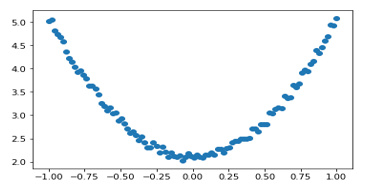
图2-14 可视化输入数据
3)初始化权重参数。
|
|
# 随机初始化参数,参数w,b为需要学习的,故需requires_grad=True w = torch.randn(1,1, dtype=dtype,requires_grad=True) b = torch.zeros(1,1, dtype=dtype, requires_grad=True) |
4)训练模型。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
lr =0.001 # 学习率 for ii in range(800): # forward:计算loss y_pred = x.pow(2).mm(w) + b loss = 0.5 * (y_pred - y) ** 2 loss = loss.sum() # backward:自动计算梯度 loss.backward() # 手动更新参数,需要用torch.no_grad()更新参数 with torch.no_grad(): w -= lr * w.grad b -= lr * b.grad # 因通过autigrad计算的梯度,会累加到grad中,故每次循环需把梯度清零 w.grad.zero_() b.grad.zero_() |
5)查看可视化训练结果。
|
|
plt.plot(x.numpy(), y_pred.detach().numpy(),'r-',label='predict',linewidth=4)#predict plt.scatter(x.numpy(), y.numpy(),color='blue',marker='o',label='true') # true data plt.xlim(-1,1) plt.ylim(2,6) plt.legend() plt.show() print(w, b) |
运行结果如图2-15所示。
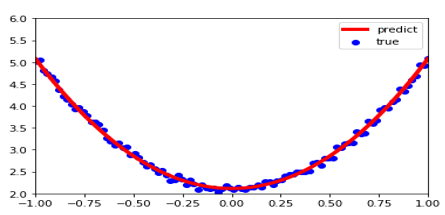
图2-15 使用 autograd的结果
tensor([[2.9645]], requires_grad=True) tensor([[2.1146]], requires_grad=True)。
这个结果与使用NumPy机器学习的差不多。
2.8 使用优化器及自动微分
使用PyTorch内置的损失函数、优化器和自动微分机制等,可大大简化整个机器学习过程。梯度更新可简化为optimizer.step(),梯度清零可使用optimizer.zero_grad()。详细代码如下。导入模块与生成数据代码与2.7小节的基本相同,只需添加导入nn模块(这个模块第3章将介绍),这里就重写了。
1)定义损失函数及优化器。
|
|
loss_func = nn.MSELoss() optimizer = torch.optim.SGD([w,b],lr = 0.001) |
2)训练模型。
|
|
for ii in range(10000): # forward:计算loss y_pred = x.pow(2).mm(w) + b loss=loss_func(y_pred,y) # backward:自动计算梯度 loss.backward() # 更新参数 optimizer.step() # 因通过autigrad计算的梯度,会累加到grad中,故每次循环需把梯度清零 optimizer.zero_grad() |
3)查看可视化运行结果。
|
|
plt.plot(x.numpy(), y_pred.detach().numpy(),'r-',label='predict',linewidth=4)#predict plt.scatter(x.numpy(), y.numpy(),color='blue',marker='o',label='true') # true data plt.xlim(-1,1) plt.ylim(2,6) plt.legend() plt.show() print(w, b) |
运行结果如图2-16所示。

图2-16 使用优化器及自动微分(autograd)的结果
tensor([[2.6369]], requires_grad=True) tensor([[2.2360]], requires_grad=True)
由此可知,使用内置损失函数、优化器及自动微分实现机器学习比较简洁,这也是深度学习普遍采用的方式。
2.9 把数据集转换带批量的迭代器
把数据集转换为带批量的迭代器,这样训练时就可进行批量处理。如果数据量比较大,采用批量处理可提升训练模型的效率及性能。
1)构建数据迭代器。
|
|
import numpy as np # 构建数据迭代器 def data_iter(features, labels, batch_size=4): num_examples = len(features) indices = list(range(num_examples)) np.random.shuffle(indices) #样本的读取顺序是随机的 for i in range(0, num_examples, batch_size): indexs = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) yield features.index_select(0, indexs), labels.index_select(0, indexs) |
2)训练模型。
|
|
for ii in range(1000): for features, labels in data_iter(x,y,10): # forward:计算loss y_pred = features.pow(2).mm(w) + b loss=loss_func(y_pred,labels) # backward:自动计算梯度 loss.backward() # 更新参数 optimizer.step() # 因通过autigrad计算的梯度,会累加到grad中,故每次循环需把梯度清零 optimizer.zero_grad() |
3)查看可视化运行结果。
|
|
y_p=x.pow(2).mm(w).detach().numpy() + b.detach().numpy() plt.plot(x.numpy(), y_p,'r-',label='predict',linewidth=4)#predict plt.scatter(x.numpy(), y.numpy(),color='blue',marker='o',label='true') # true data plt.xlim(-1,1) plt.ylim(2,6) plt.legend() plt.show() print(w, b) |
运行结果如图2-17所示。
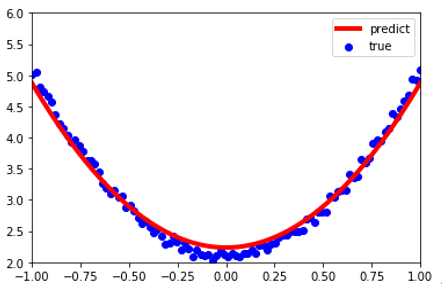
图2-17 使用数据迭代器、优化器和自动微分(autograd)的结果
tensor([[2.6370]], requires_grad=True) tensor([[2.2360]], requires_grad=True)
2.10 使用TensorFlow2架构实现机器学习
2.6节用NumPy实现了回归分析,2.7节用PyTorch的autograd及Tensor实现了这个任务。这节我们用深度学习的另一个框架TensorFlow实现该回归分析任务,大家可比较一下不同架构之间的区别。为便于比较,这里使用TensorFlow 2实现这个任务。
1)导入库及生成训练数据。
|
|
import tensorflow as tf import numpy as np from matplotlib import pyplot as plt %matplotlib inline |
2)生成训练数据,并初始化参数。
|
|
#生成训练数据 np.random.seed(100) x = np.linspace(-1, 1, 100).reshape(100,1) y = 3*np.power(x, 2) +2+ 0.2*np.random.rand(x.size).reshape(100,1) # 创建权重变量w和b,并用随机值初始化. # TensorFlow 的变量在整个计算图保存其值. w = tf.Variable(tf.random.uniform([1], 0, 1.0)) b = tf.Variable(tf.zeros([1])) |
3)构建模型。
|
|
# 定义模型 class CustNet: #正向传播 def __call__(self,x): return np.power(x,2)*w + b # 损失函数 def loss_func(self,y_true,y_pred): return tf.reduce_mean((y_true - y_pred)**2/2) model=CustNet() |
4)训练模型。
|
|
epochs=14000 for epoch in tf.range(1,epochs): with tf.GradientTape() as tape: predictions = model(x) loss = model.loss_func(y, predictions) # 反向传播求梯度 dw,db = tape.gradient(loss,[w,b]) # 梯度下降法更新参数 w.assign(w - 0.001*dw) b.assign(b - 0.001*db) |
5)查看可视化运行结果。
|
|
# 可视化结果 plt.figure() plt.scatter(x,y,color='blue',marker='o',label='true') plt.plot (x, b + w*x**2,'r-',label='predict',linewidth=4) |
运行结果如图2-18所示。
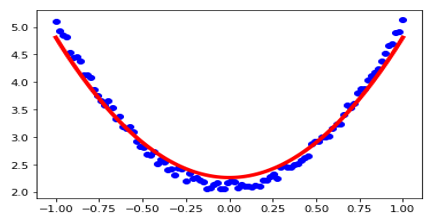
图2-18 使用Tensorflow的结果
2.11 小结
本章主要介绍PyTorch的基础知识,这些内容是后续章节的重要支撑。首先介绍了PyTorch的安装配置,然后介绍了PyTorch的重要数据结构Tensor。Tensor类似于NumPy的数据结构,但Tensor提供GPU加速及自动求导等技术。最后分别用NumPy、Tensor、autograd、Optimizer和TensorFlow2等技术分别实现同一个机器学习任务。















![X=\left[\begin{matrix} 2\cr 0 \cr 3\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_6a6e494f29a832978f6137fea4f47b62.gif)
![X^T=[2,0,3]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_cb76eb1a85054ae457f1c08cd95e0515.gif)

![Y=\left[\begin{matrix} 1\cr 5 \cr 9\end{matrix}\right]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_28920b2ed27650661a6265cc3fdd7f71.gif)
![X^T Y=[2,0,3]\cdot \left[\begin{matrix} 1\cr 5 \cr 9\end{matrix}\right]=2\times 1+0\times 5+3\times 9=29](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_af8d3f0b7b259a755b777d2b8c48338f.gif)








![w=[\omega_1, \omega_2,\dots, \omega_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_bbf770a67169b8b8d3766290e321fec1.gif)
![X=[x_1, x_2,\dots, x_n]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_73a32a0aecbab97263a6d3e21b78ab45.gif)











































































![X=[x_1,x_2]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_8de545821487bd0e59c2a63bba38810d.gif)
![Y=[x_1^2+3,x_2^2+3]](http://www.feiguyunai.com/wp-content/plugins/latex/cache/tex_c703a1571d623ee3a87630f1639a035f.gif)